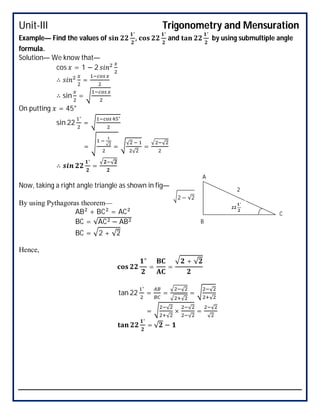
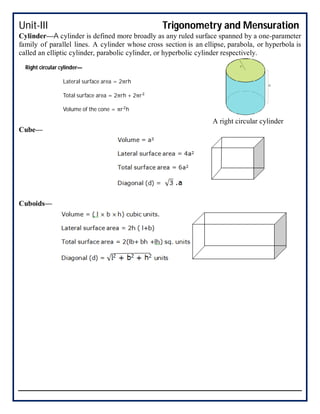
This document covers trigonometry and mensuration topics including trigonometric identities, compound angle formulas, double angle formulas, sub-multiple angle formulas, properties of triangles, and mensuration of triangles, quadrilaterals, circles, spheres, cones, cylinders, cubes and cuboids. Examples are provided to demonstrate using sub-multiple angle formulas to find trigonometric values of particular angles. Exercises at the end test comprehension of finding trigonometric values, properties of different types of triangles including area calculations, volumes of cones and cylinders, and references are listed.

1. Trigonometry and Mensuration
Course- Diploma
Semester-II
Subject- Advanced Mathematics
Unit- III
RAI UNIVERSITY, AHMEDABAD

2. Unit-III Trigonometry and Mensuration
3.1 Trigonometry
3.1.1 Trigonometric Identities—
1. sin + cos = 1
2. sec − tan = 1
3. cosec − cot = 1
3.1.2 Compound angles formulas—
1. ( + ) = +
2. ( − ) = −
3. ( + ) = −
4. ( − ) = +
5. ( + ) =
6. ( − ) =
7. ( + ) =
8. ( − ) =
3.1.3 Double angle formulas—
1. 2 = 2 =
2. 2 = − = 2 − 1 = 1 − 2 =
3. 2 =
4. 2 =
3.1.4 Sub multiple angle formulas—
1. = 2
=
2. = −
= 2 − 1
= 1 − 2
=
3. =
4. =

3. Unit-III Trigonometry and Mensuration
Example— Find the values of
°
,
°
and
°
by using submultiple angle
formula.
Solution— We know that—
cos = 1 − 2
∴ =
∴ sin =
On putting = 45°
sin 22
°
=
°
= √
=
√
√
=
√
∴
°
=
√
Now, taking a right angle triangle as shown in fig—
By using Pythagoras theorem—
AB + BC = AC
BC = √AC − AB
BC = 2 + √2
Hence,
°
= =
+ √
tan 22
°
= =
√
√
=
√
√
=
√
√
×
√
√
=
√
√
°
= √ −
°
2 − √2
2
A
B
C

4. Unit-III Trigonometry and Mensuration
Example— Find the values of °, ° and ° by using sub multiple angle
formula.
Solution— We know that— sin = 2 sin cos
On putting = 72°
sin 72° = 2 sin 36° cos 36°
sin(90° − 18°) = 2(2 sin 18° cos 18°)(1 − 2 sin 18°)
cos 18° = 4 18° 18°(1 − 2 18°)
1 = 4 sin 18° (1 − 2 sin 18°)
8 sin 18° − 4 sin 18° + 1 = 0
(2 sin 18° − 1)(4 sin 18° + 2 sin 18° − 1) = 0
but sin 18° ≠ , therefore—
4 sin 18° + 2 sin 18° − 1 = 0
∴ sin 18° =
√
° =
√ −
Now, taking a right angle triangle as shown in fig—
By using Pythagoras theorem—
AB + BC = AC
BC = √AC − AB
BC = 10 + 2√5
Hence,
° = =
+ √
tan 18° = =
√
√
=
√
√
=
√
√
×
√
√
= 1 −
√
° = −
√
Selected + sign, since ° > 0
°
√5 − 1
4
B C
A

5. Unit-III Trigonometry and Mensuration
3.1.5 Properties of triangle—
1. sine rule—
2. Cosine rule—
3. Relation between area of triangle, angles and its sides—
Where, 2s = a + b + c
∆ = area of triangle
R = radius of circum circle
r = radius of incircle

6. Unit-III Trigonometry and Mensuration
4. Half angle formulae—
EXERCISE
Question— Find the values of sin 72 , cos 72 and tan 72 .
Question— Find the sine of the angles A,B and C of triangle ABC having sides = 3, = 4
and = 5.
Question— Find the in-circle radius of the triangle having its side 5cm, 12cm and 13cm.
Question— Find the circum radius of the circle inscribing the triangle having its sides equal to
8cm, 15cm and 17cm.
Question— Find the area of the triangle having its sides 4cm, 4cm and 6cm.

7. Unit-III Trigonometry and Mensuration
3.2 Mensuration
3.2.1 Introduction—anything concerned with measuring, calculating and estimating lengths,
areas and volumes, as well as the construction of objects, comes under the Mensuration.
Therefore, units have an important role in Mensuration. Some standard units with their
conversion are listed below—
Length Area Volume Weight
1 Km 1000 m 1 m 10000 cm 1 m 1000 litres 1 tonne 1000 Kg
1 m 100 cm 1 cm 100 mm 1 litre 1000 ml 1 Kg 1000 g
1cm 10 mm 1 cm 1 ml
3.2.2 Triangle—a triangle is a polygon with three edges and three vertices. It is one of the basic
shapes in geometry. A triangle with vertices A, B and C is denoted by ∆ABC . Shape of a
triangle is shown below—
A
B C
Existence of a triangle—the triangle inequality states that the sum of the lengths of any two
sides of a triangle must be greater than or equal to the length of the third side. That sum can
equal the length of the third side only in the case of a degenerate triangle, one with collinear
vertices. It is not possible for that sum to be less than the length of the third side.
There are two important parameter related to a triangle are—
Area of Triangle— It depends upon the shape and size of the triangle.
Perimeter— It is equal to the sum of the sides of the triangle.
Perimeter = AB + BC + CA
Some important types of triangle are listed below— A
1. Right angle triangle— Square of any one side of triangle is equal
to the sum of squares of other sides.
Here, AB + BC = AC and triangle is right angled at B.
Perimeter = AB + BC + CA B C
Area = (AB)(BC)
Note— For any ∆ABC, ∠ + ∠ + ∠ = °

8. Unit-III Trigonometry and Mensuration
2. Isosceles triangle—A triangle having two equal sides is called as isosceles triangle.
In this diagram side AB and AC are equals. Hence, ∠B and ∠C are
equals. A
Perimeter = 2AB + BC
Area = (BC)√4AB − BC
B C
3. Equilateral triangle— A triangle having all sides equal is called as equilateral triangle.
In this diagram side AB, BC and AC all are equal. Hence, ∠A , ∠B and ∠C are
equals. A
Perimeter = 3AB
Area =
√
AB
B C
Quadrilateral— a quadrilateral is a polygon with four sides and four vertices or corners.
There are two types of quadrilateral— A
1. Planar quadrilateral—The interior angles of a simple (and planar)
quadrilateral ABCD add up to 360 degrees of arc,
that is— B D
C
2. Crossed quadrilateral— In a crossed quadrilateral, the four A
interior angles on either side of the crossing add up to 720°.
B C D
Parallelogram— A four-sided polygon with two pairs of parallel and equal sides. The
following is a parallelogram—
= ×
Rectangle— A rectangle is a parallelogram with 4 right angles. The following is a rectangle—
h
b

9. Unit-III Trigonometry and Mensuration
Square—A square is a rectangle with 4 equal sides. The following is square—
Rhombus— A rhombus is a parallelogram with 4 equal sides. The following is a rhombus—
Trapezoid— A trapezoid is a quadrilateral with only one pair of parallel sides. The following
are trapezoids—
1. Scalene trapezoid— A scalene trapezoid is a trapezoid with no equal sides. The
following is a scalene trapezoid—
2. Right-angled trapezoid— A right-angled is a trapezoid with two right angles. The
following is a right-angle trapezoid—
3. Isosceles trapezoid— In an isosceles trapezoid, non-parallel sides are equal.
The following is an isosceles trapezoid—

10. Unit-III Trigonometry and Mensuration
Circle—
Semicircle—
Sphere— Sphere is a locus of the points having fixed distance from a fixed point in three
dimensional planes.
Cone— It is the solid figure bounded by a base in a plane and by a surface (called the lateral
surface) formed by the locus of all straight line segments joining the apex to the perimeter of the
base.
Volume of the sphere =
4
3
πr
Surface area of the sphere = 4πr
A right circular cone and an oblique
circular cone
Right circular cone—

11. Unit-III Trigonometry and Mensuration
Cylinder—A cylinder is defined more broadly as any ruled surface spanned by a one-parameter
family of parallel lines. A cylinder whose cross section is an ellipse, parabola, or hyperbola is
called an elliptic cylinder, parabolic cylinder, or hyperbolic cylinder respectively.
A right circular cylinder
Cube—
Cuboids—
Right circular cylinder—
Lateral surface area = 2πrh
Total surface area = 2πrh + 2πr
Volume of the cone = πr h

12. Unit-III Trigonometry and Mensuration
EXERCISE
Question— Three sides of a triangle are AB=3 cm, BC=4cm and CA=5cm. Discuss about the
type of triangle. Also find its area.
Question— A triangle having two equal sides of length 12 cm and third side of length 9 cm.
Find the area of the triangle.
Question— Find the sides of an equilateral triangle having area 173 sq. cm.
Question— Find the volume of a cone having base radius 5cm and height 12cm.
Question— Find the volume of a cylinder having base radius and height both equals to 7cm.

13. Unit-III Trigonometry and Mensuration
References—
1. en.wikipedia.org/wiki/Trigonometry
2. www.mathsisfun.com
3. https://www.khanacademy.org/math/trigonometry
4. www.sosmath.com
5. www.themathpage.com
6. www.clarku.edu
7. en.wikibooks.org/wiki/Trigonometry
8. www.cimt.plymouth.ac.uk
9. www.bbc.co.uk