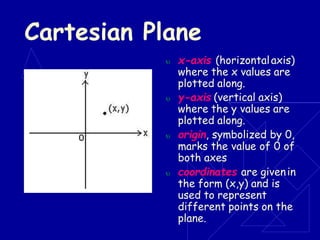
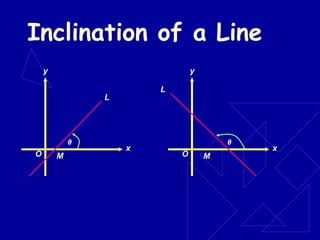
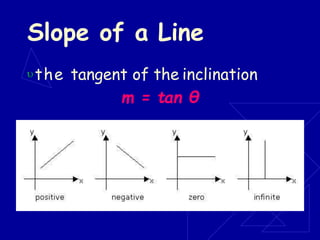
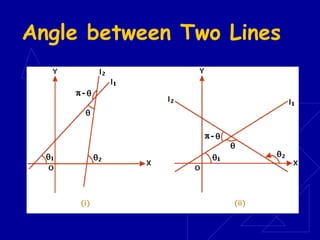
Analytic geometry is a branch of mathematics that uses algebraic equations to describe geometric figures in a coordinate system. It was introduced in the 1600s by Descartes and Fermat and allowed geometry and algebra to be linked through coordinate systems. The Cartesian plane forms the basis of analytic geometry by allowing algebraic equations to be graphically represented through coordinate points and mapping geometric shapes like lines, circles, and conics to algebraic equations.

1. Analytic Geometry
Basic Concepts

2. Analytic Geometry
 a branch ofmathematics
which uses algebraic
equations to describe the size
and position of geometric
figures on a coordinate
system.

3. Analytic Geometry
 It was introduced in the 1630s, an
important mathematical development,
for it laid the foundations for
modern mathematics as well as aided
the development of calculus.
 Rene Descartes (1596-1650) and
Pierre de Fermat (1601-1665),
French mathematicians,
independently developed the
foundations for analytic geometry.

4. Analytic Geometry
the link between algebra and
geometry was made possible by the
development of a coordinate
system which allowed geometric
ideas, such as point and line, to be
described in algebraic terms like
real numbers and equations.
also known as Cartesian geometry
or coordinate geometry.

5. Analytic Geometry
 the use of a coordinate system to
relate geometric points to real
numbers is the central idea of analytical
geometry.
 by defining each point with a unique
set of real numbers, geometric figures
such as lines, circles, and conics can be
described with algebraic equations.

6. Cartesian Plane
 The Cartesian plane, the basis of analytic
geometry, allows algebraic equations to be
graphically represented, in a process called
graphing.
 It is actually the graphical representation
of an algebraic equation, of any form --
graphs of polynomials, rational functions,
conic sections, hyperbolas, exponential and
logarithmic functions, trigonometric
functions, and even vectors.

7. Cartesian Plane
 x-axis (horizontalaxis)
where the x values are
plotted along.
 y-axis (vertical axis)
where the y values are
plotted along.
 origin, symbolized by 0,
marks the value of 0 of
both axes
 coordinates are givenin
the form (x,y) and is
used to represent
different points on the
plane.

8. Cartesian Coordinate System
y
5
4
3
2
1
x
-5 -4 -3 -2 -1 0 1 2 3 4 5
-1
-2
-3
-4
-5
I
(+, +)
II
(-, +)
III
(-, -)
IV
(+, -)

9. Cartesian Coordinate
System
O
x
y

10. Distance between Two Points

11. Midpoint between Two Points

12. Inclination of a Line
The smallest angle θ, greater
than or equal to 0°, that the line
makes with the positive direction
of the x-axis (0° ≤ θ < 180°)
Inclination of a horizontal line is
0.

13. Inclination of a Line
O
θ
M
x
y
L
O M
θ
x
y
L

14. Slope of a Line
the tangent of the inclination
m = tan θ

15. Slope of a Line
passing through two given points,
P1(x1, y1) and P2(x2,y2) is equal to
the difference of the ordinates
divided by the differences of the
abscissas taken in the same order

16. Theorems on Slope
Two non-vertical lines are parallel
if, and only if, their slopes are
equal.
Two slant lines are perpendicular
if, and only if, the slope of one is
the negative reciprocal of the
slope of the other.

17. Angle between Two Lines

18. Angle between Two Lines
 If θ is angle, measured counterclockwise,
between two lines, then
 where m2is the slope of the terminal
side and m1is the slope of the initial side