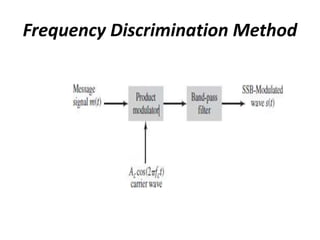
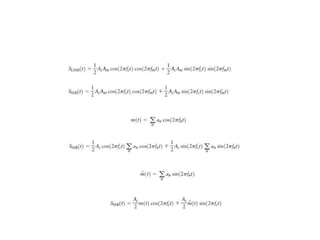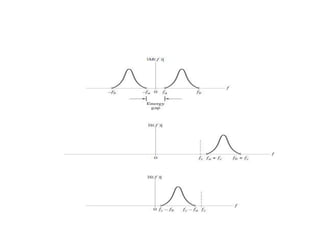
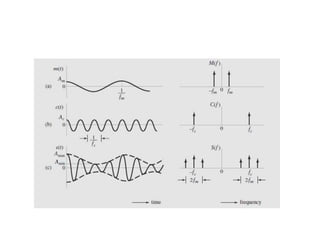
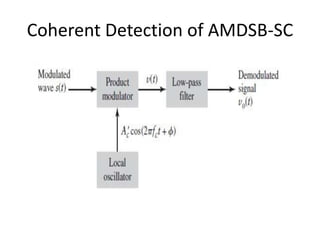
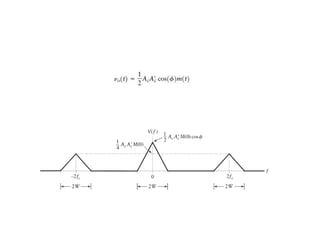
1. The document discusses amplitude modulation (AM) techniques such as AM double sideband full carrier (AMDSB-FC), AM double sideband suppressed carrier (AMDSB-SC), and single sideband (SSB) modulation. 2. It explains that AMDSB-FC and AMDSB-SC use two sidebands which contain redundant information, wasting channel bandwidth. SSB modulation suppresses one sideband to improve bandwidth efficiency. 3. Key aspects of envelope detection and its use in demodulating AM signals are covered, along with the need for coherent detection of AMDSB-SC to avoid phase errors.

3. • c(t)=𝐴𝑐cos 2𝜋𝑓𝑐t is carrier
• m(t) is message
• AM DSB FC is
• m(t) c(t)+c(t)
• m(t) 𝐴𝑐cos 2𝜋𝑓𝑐t+𝐴𝑐cos 2𝜋𝑓𝑐t
• 𝐴𝑐cos 2𝜋𝑓𝑐t[m(t)+1]
• 𝑠 𝑡 = 𝐴𝑐[1+m(t)] cos 2𝜋𝑓𝑐t
• m(t) cos 2𝜋𝑓𝑐t+𝐴𝑐cos 2𝜋𝑓𝑐t

4. • Envelope of s(t) has same shape as m(t) if the
following conditions are satisfied.
• 1. 𝑚(𝑡) < 1
• If this condition is fulfilled 1+m(t) will be more
than 0. In this condition 𝑠 𝑡 = 𝐴𝑐[1+m(t)] will be
positive.
• If 1+m(t)< 0 for some duration, when m(t)
crosses zero there will be phase reversal, which
means there is distortion. This condition is called
overmodulation.

6. 2. The carrier frequency 𝑓𝑐 ≫ 𝑊 where W is message
bandwidth.
m(t) 𝐴𝑐cos 2𝜋𝑓𝑐t+𝐴𝑐cos 2𝜋𝑓𝑐t
m(t)=a 𝑚𝑛(t) where a=
𝑚(𝑡) 𝑚𝑎𝑥
𝐴𝑐
is called modulation index
and 𝑚𝑛(t) is called normalised modulating signal where its
minimum value is
-1.
𝑚𝑛 𝑡 =
m(t)
𝑚(𝑡) 𝑚𝑎𝑥
𝑠 𝑡 = 𝐴𝑐[1+ a 𝑚𝑛(t) ] cos 2𝜋𝑓𝑐t
𝑠 𝑡 = 𝐴𝑐[1+ 𝑘𝑎 𝑚 (t) ] cos 2𝜋𝑓𝑐t, where 𝑘𝑎=1/𝐴𝑐
𝑘𝑎 is called amplitude sensitivity

11. • Consider a modulating wave that consists of a single
tone or frequency component;
that is,
m(t)=𝐴𝑚cos 2𝜋𝑓𝑚t
AM wave is therefore given by
𝑠 𝑡 = 𝐴𝑐[1+ a cos 2𝜋𝑓𝑚t ] cos 2𝜋𝑓𝑐t
𝐴𝑚𝑎𝑥
𝐴𝑚𝑖𝑛
=
𝐴𝑐(1+𝑎)
𝐴𝑐(1−𝑎)
This equation gives
a=
𝐴𝑚𝑎𝑥−𝐴𝑚𝑖𝑛
𝐴𝑚𝑎𝑥+𝐴𝑚𝑖𝑛

12. • 𝑠 𝑡 = 𝐴𝑐[1+ a cos 2𝜋𝑓𝑚t ] cos 2𝜋𝑓𝑐t
= 𝐴𝑐 cos 2𝜋𝑓𝑐t+ a 𝐴𝑐 cos 2𝜋𝑓𝑚t cos 2𝜋𝑓𝑐t
= 𝐴𝑐 cos 2𝜋𝑓𝑐t+
a 𝐴𝑐
2
cos 2𝜋 (𝑓𝑐− 𝑓𝑚)t+
a 𝐴𝑐
2
cos 2𝜋 (𝑓𝑐+𝑓𝑚)t
S(f)=
𝐴𝑐
2
𝛿(𝑓 + 𝑓𝑐)+
𝑎𝐴𝑐
4
𝛿(𝑓 + [𝑓𝑐−𝑓𝑚])+
𝑎𝐴𝑐
4
𝛿(𝑓 −
[𝑓𝑐−𝑓𝑚])+
𝑎𝐴𝑐
4
𝛿(𝑓 + [𝑓𝑐−𝑓𝑚])+
𝑎𝐴𝑐
4
𝛿(𝑓 +
[𝑓𝑐+𝑓𝑚])+
𝑎𝐴𝑐
4
𝛿(𝑓 − [𝑓𝑐+𝑓𝑚])

14. • Signal power in carrier=
𝐴𝑐
2
2
•
[
𝑎2𝐴𝑐
4
2
]
2
=
𝑎2𝐴𝑐
8
2
•
[
𝑎2𝐴𝑐
4
2
]
2
=
𝑎2𝐴𝑐
8
2
• The ratio of the total sideband power to the total power in
the modulated wave is equal to
𝑎2
2+𝑎2 which depends only
on the modulation factor.
• If 100 percent modulation is used the total power in the
two side frequencies of the resulting AM wave is only one-
third of the total power in the modulated wave.

16. • In this, 𝑘𝑎=
2𝑎2
𝑎1
or
𝑎
𝑚(𝑡) 𝑚𝑎𝑥
=
2𝑎2
𝑎1

17. • The demodulation of an AM wave can be
accomplished by means of a simple and yet
highly effective circuit called the envelope
detector two practical conditions are satisfied:
• 1. The AM wave is narrowband, which means
that the carrier frequency is large compared
to the message bandwidth.
• 2. The percentage modulation in the AM wave
is less than 100 percent.

18. • On a positive half-cycle of the input signal, the
diode is forward-biased and the capacitor C
charges up rapidly to the peak value of the
input signal.
• When the input signal falls below this value,
the diode becomes reverse-biased and the
capacitor C discharges slowly through the load
resistor

19. • The discharging process continues until the
next positive half-cycle.
• When the input signal becomes greater than
the voltage across the capacitor, the diode
conducts again and the process is repeated.
• We assume that the diode is ideal, presenting
Resistance 𝑟𝑓 to current flow in the forward-
biased region and infinite resistance in the
reverse-biased region.

20. • AM wave applied to the envelope detector is
supplied by a voltage source of internal
impedance 𝑅𝑠
• The charging time constant (𝑟𝑓+ 𝑅𝑠)C must be
short compared with the carrier period —that is,
• (𝑟𝑓+ 𝑅𝑠)C≪
1
𝑓𝑐
so that the capacitor C charges rapidly and
thereby follows the applied voltage up to the
positive peak when the diode is conducting.

21. • The discharging time constant 𝑅𝑙C must be long
enough to ensure that the capacitor discharges
slowly through the load resistor 𝑅𝑙between
positive peaks of the carrier wave, but not so long
that the capacitor voltage will not discharge at
the maximum rate of change of the modulating
wave—that is,
1
𝑓𝑐
≪ 𝑅𝑙C≪
1
𝑊
where W is the message bandwidth.

24. AMDSB-SC with Single Tone
Modulating Signal

25. • What is the average power in the lower or
upper side-frequency of a DSB-SC signal,
expressed as a percentage of the average
power in the DSB-SC modulated signal?

26. Coherent Detection of AMDSB-SC

29. • The demodulated signal is therefore proportional to when
the phase error is a constant.
• The amplitude of this demodulated signal is maximum
when cos∅ is maximum and it is minimum (zero) when
cos∅ is minimum.
• The zero demodulated signal, which occurs for cos∅ = 0
represents the quadrature null effect, which is an inherent
property of coherent detection.
• Thus the phase error in the local oscillator causes the
detector output to be attenuated by a factor equal to cos∅.
As long as the phase error is constant, the detector output
provides an undistorted version of the message signal

30. • In practice, however, we usually find that the phase
error varies randomly with time, due to random
variations in the communication channel.
• The result is that at the detector output, the
multiplying factor would also vary randomly with time,
which is obviously undesirable. The output needs to be
calculated by applying expectation.
• Therefore, provision must be made in the system to
maintain the local oscillator in the receiver in
synchronism, in both frequency and phase, with the
carrier wave used to generate the DSB-SC modulated
signal in the transmitter.

31. Single-Sideband Modulation
• Major limitation of AMDSB-FC and AMDSB-SC is that they use two
sidebands which contain same information. This causes more
channel bandwidth without giving extra information.
• We can suppress one of the two sidebands without loss of
information
• When we do this modification of DSB-SC modulation we get a
scheme called single sideband (SSB) modulation.
• In effect, SSB modulation relies solely on thelower sideband or
upper sideband to transmit the message signal across a
communication channel.
• Depending on which particular sideband is actually transmitted, we
speak of lower SSB or upper SSB modulation.

35. Frequency Discrimination Method