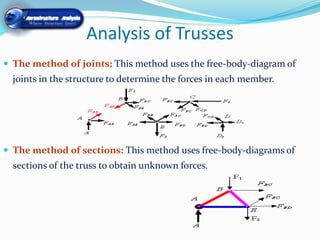
The document provides information about: 1) The objectives of the aeronautical engineering project, which are to teach students how to analyze load-bearing structures and various analysis methods. 2) The different types of stresses acting on structures like normal stress, shearing stress, and how they relate to forces and deformations. 3) Additional structural analysis concepts covered include truss analysis methods, strains under axial loading, temperature effects, and torsion in circular and thin-walled members.

2. Why wiki ?
 A wiki is a website designed for multiple
people to collaborate by adding and
editing content. Aerostructure Analysis
wiki is an example of a wiki. A wiki farm
is a collection of individual wikis, usually
hosted by the same website. Browse
through a list of wikis by category

3. Wiki

4. The problems which we faced
1. When we started the project we found that having the
material must be with it’s references, but we found that
there is a lot of material without a references so couldn’t
put it in the wiki. And we solved this problem by adding
some videos and presentations instead of this unlicensed
data.
2. The tools which wikispaces provide to us are too limited
but somehow it was effective.
3. We couldn’t make a better design because of this limited
tools and it needs $ to open this tools on wikispaces.
4. Other team members weren’t able to deal with the site
and we sloved this problems by a several meetings.
5. Our logo

5. 1st problem and how we solved it

6. 2nd problem and how we solved it

7. 3rd problem and how we solved it

8. Objectives
 The main objective of the project about
this course is to provide future aeronautical
engineers with the means of analyzing and
designing various load bearing structures.
This can be done by learning them How to analyze a system of
forces and obtain the reactions at the supports of structures and
How to analyse the forces in plain trusses. Later, they will study the
nature of stress and strain, and the properties of cross sections,
finally, they will be introduced to the forces and stresses in
members subject to axial, torsion, and bending loading.

9. Analysis of Trusses
 The method of joints: This method uses the free-body-diagram of
joints in the structure to determine the forces in each member.
 The method of sections: This method uses free-body-diagrams of
sections of the truss to obtain unknown forces.

11. Normal Stress and Shearing Stress
 Definition : - Stress is a measure of the
average force per unit area of a surface
within a deformable body on which
internal forces act. It is a measure of the intensity of the internal
forces acting between particles of a deformable body across
imaginary internal surfaces

13. Normal Strain Under Axial Loading
 Normal Strain: It is the deformation in the material due to the effect of
normal force on it's cross section area.
 It Denoted by: ε the deformation / normal length..
=
 It's unit: it has no unit as it is a ratio between to similar quantities.
 Axial Loading: It is the normal stress due to the effect of normal force
affect on area.
 It Denoted by: σ = normal force / area
 It's unit: N/m2

15. True Stress and True Strain
 There are two kinds of stress; Engineering stress and True stress.
 Engineering stress: it is the force divided by the initial cross section area
 True stress: it is obtained by dividing the force by the instantaneous cross
sectional area.
 Engineering strain: it can be obtained by the dividing of the total
deformation occurred on the specimen by the initial length
 True strain: it can be obtained by recording the length of the specimen and
determine the deformation in each record then divide this deformation on
the corresponding length of the specimen and with the summation of all
stains in all records (or by integration) we can get the true strain εt =
ln(L/L0)

17. Deformations of Members under Axial
Loading
 Consider a homogeneous (constant E) rod of
length L and of cross section area A subjected
to a normal force P to make in it a deformation
∆L and strain ε and stress σ , then from Hook's
law σ = Eε , ε = P/AE and since ε = ∆L/L , ∆L = ε L , then ∆L = PL/AE
 If the rod is consists of more than one martial and of different cross
section area then the total deformation on the rod is the summation of
the deformation in each portion ∆L = ∑I (Pi . Li / Ai . Ei)

19. Statically Indeterminate Problems
 Statically Indeterminate Problems
They are problems in which the internal forces cannot be determined
from statics alone. In fact, in most of these problems the reactions
themselves-which are external forces-cannot be determined by simply
drawing a free-body diagram of the member and writing the
corresponding equilibrium equations. The equilibrium equations must
be complemented by relations involving deformations obtained by
considering the geometry of the problem. Because statics is not
sufficient to determine either the reactions or the internal forces,
problems of this type are said to be statically indeterminate.

21. Problems Involving Temperature
Changes
 Let us first consider a homogeneous rod AB of uniform cross section,
which rests freely on a smooth horizontal surface. If the temperature of
the rod is raised by ∆T, we observe that the rod elongates by an amount
∆L which is proportional to both the temperature change ∆T and the
length L of the rod, then ∆L = α ∆T L (Note if the rod is fixed between
two fixed walls then its area will increase and then it's volume also, the
stain = 0 but there is stress) Where α is a constant characteristic of the
material, called the coefficient of thermal expansion and it has a unit of
a quantity per degree C.

23. Poisson's Ratio
 Meaning of Poisson's ratio:
Poisson's ratio is the ratio of transverse contraction strain to longitudinal
extension strain in the direction of stretching force. Tensile deformation
is considered positive and compressive deformation is considered
negative. The definition of Poisson's ratio contains a minus sign so that
normal materials have a positive ratio. Poisson's ratio, also called Poisson
ratio or the Poisson coefficient, is usually represented as a lower case
Greek nu, ν .
· Poisson ratio = - lateral strain / axial strain .

25. Multiaxial Loading; Generalized Hooke’s
Law
 The generalized Hooke's Law can be used to predict the deformations
caused in a given material by an arbitrary combination of stresses.

27. Torsion
 Difference between Bars and Shafts:
Bars are members that are subjected to an axial loading along it's axis
but Shafts are members that are subjected to twist or torque
 Torsion in circular Shafts
 Torsion in thin structures
 Torsion in thin walled members

29. Questions

30. Thanks for all