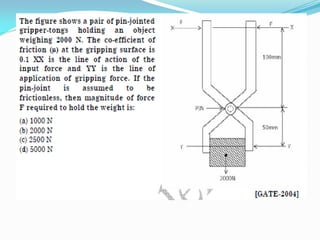
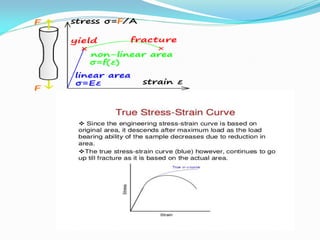
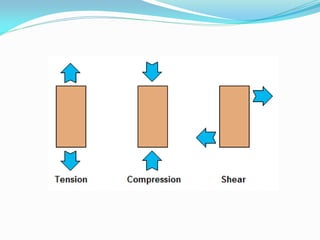
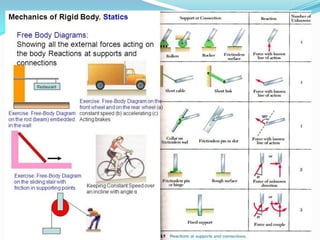
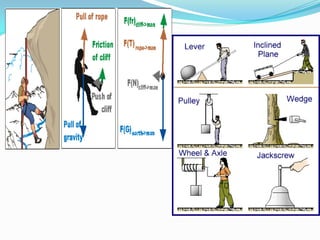
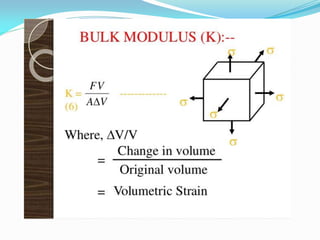
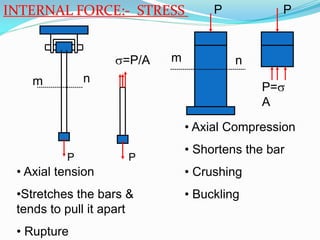
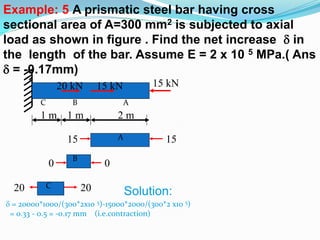
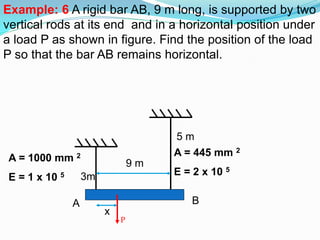
This document provides an introduction to strength of materials (SOM). It defines key terms like strength, stiffness, stability, and durability. It discusses the basic problem in SOM as developing methods to design structural elements that consider strength, stiffness, stability, and economy. It also outlines the main hypotheses in SOM, including the material being continuous, homogeneous, and isotropic. It then discusses different types of stresses like tensile, compressive, and shear stresses. It provides stress-strain curves for ductile materials and defines modulus of elasticity. Examples of calculating stresses and strains in structural elements are also provided.

1. Santosh Hiremath
Asst Professor
GHRCEM Pune

2. CONTENTS
 Introduction
 What is SOM?
 Types of forces
 Types of loads
 Types of materials
 Types of stresses
 Types of strain
 Hooke’s Law
 Application of SOM

3. Introduction
Nowadays the building of structures, machines and
other engineering structures is impossible without projects
previously drawn. The project consists of the drawings and
explanation notes presenting the dimensions of the
construction elements, the materials necessary for their
building and the technology for their building.
The dimensions of the elements and details depend on
the characteristics of the used materials and the external forces
acting upon the structures and they have to be determined
carefully during the design procedure.

4. The structure must be reliable as well as economical
during the exploitation process. The reliability is guaranteed
when the definite strength, stiffness, stability and durability
are taken in mind in the structure.
The economy of the construction depends on the
material’s expenditure, on the new technology introduction
and on the cheaper materials application. It is obvious that
the reliability and the economy are opposite requirements.
Because of that, the Strength of Materials relies on the
experience as well as the theory and is a science in
development.

5. Strength: is the ability of the structure to resist the influence
of the external forces acting upon it without any failure.
Stiffness: is the ability of the structure to resist the strains
caused by the external forces acting upon it.
Stability: is the property of the structure to keep its initial
position of equilibrium.
Durability: is the property of the structure to save its
strength, stiffness and stability during the exploitation time.
Strength of Materials widely relies on the Theoretical
Mechanics, Mathematics and Physics. Besides, it is the basis
of the other subjects in the engineering practice.

7. BASIC PROBLEM OF THE STRENGTH
OF MATERIALS
 The basic problem of the science is development of
engineering methods to design the structure elements
applying the restraining conditions about the strength,
stiffness and stability of the structure when the
definite durability as well as economy is given.

8. REAL OBJECT AND CORRESPONDING
COMPUTATIONAL SCHEME
 To examine the real object a correct corresponding
computational scheme must be chosen. The computational
scheme is a real body for which the unessential attributes
are eliminated. To choose the correct computational
scheme the main hypotheses of Strength of materials have
to be introduced.

9. MAIN HYPOTHESES
 Hypotheses about the material building the body
1. Hypothesis of the material continuity
The material is uniformly distributed in a whole
body volume.
2. Hypothesis of the material homogeneity
All points of the body have the same material
properties.

10. 3.Hypothesis of the material isotropy
The material properties are the same in each direction
of a body.
4. Hypothesis of the deformability of the body
Contrary to the Theoretical Mechanics studying the
rigid bodies, Strength of Materials studies the bodies
possessing the ability to deform, i.e. the ability to change its
initial shape and dimensions under the action of external
forces.
The deformations at each point are assumed to be
small relative to the dimensions of construction. Then, their
influence onto the mutual positions of the loads can be
neglected (the calculations will be made about the
undeformed construction).

11. 5.Hypothesis of the elasticity
Elasticity is the ability of the body to restore its
initial shape and dimensions when the acting forces
have been removed
 Hypotheses about the shape of the body
The basic problem of Strength of Materials is
referred to the case of the beam type bodies. The
beam is a body which length is significant bigger
than the cross-sectional dimensions.

12.  Hypothesis of the planar cross-sections
(Bernoulli’s hypothesis)
Each planar cross-section normal to the axis of the beam
before the deformation remains planar and normal to
the same axis after deformation.

13.  Rigid body – a body consisting of particles the distances
between which do not change
 Deformable body – a body consisting of particles the
distances between which change. A deformable body is a
rigid one only to the definite loading.
 Friction – phenomenon of the emergence of forces
tangential to the contact surface of two bodies.

19. Stress
 When an external force is applied on a body, it
undergoes deformation which is resisted by the body.
The magnitude of the resisting force is numerically
equal to the applied force. This internal resisting force
per unit area of the body is known as stress.
 In equation form: σ = P/A,
 Units are: N/m2, kN/m2 MPa (Mega Pascal), Psi
(lb/in2), psf (lb/ft2), Ksi (kips/in2), ksf (kips/ft2)

20. P is expressed in Newton (N) and A, original area, in square
meters (m2), the stress σ will be
expresses in N/ m2. This unit is called Pascal (Pa).
As Pascal is a small quantity, in practice, multiples of this
unit is used.
1 kPa = 103 Pa = 103 N/ m2 (kPa = Kilo Pascal)
1 MPa = 106 Pa = 106 N/ m2 = 1 N/mm2 (MPa = Mega
Pascal)
1 GPa = 109 Pa = 109 N/ m2 (GPa = Giga Pascal)
Let us take an example: A rod 10 mm ×10 mm cross-
section is carrying an axial tensile load 10
kN. In this rod the tensile stress developed is given by

21. Torsion is a type of deformation in which the transverse
sections of a beam twist relative to each other under the
action of external torsion moments only. The
external forces situated normally to the beam axis
cause the torsion moments because they do not
intersect the axis. The torsion moments’ planes of
action are perpendicular to the longitudinal beam
axis

25. Tensile stress (σt)
If σ > 0 the stress is tensile. i.e. The fibres of the component
tend to elongate due to the external force. A member
subjected to an external force tensile P and tensile stress
distribution due to the force is shown in the given figure.
Compressive stress (σc)
If σ < 0 the stress is compressive. i.e. The fibres of the
component tend to shorten due to the external force. A
member subjected to an external compressive force P and
compressive stress distribution due to the force is shown in
the given figure.

26. Shear stress ( τ )
When forces are transmitted from one part of a body to other,
the stresses developed in a plane parallel to the applied force are
the shear stress. Shear stress acts parallel to plane of interest.
Forces P is applied transversely to the member AB as shown. The
corresponding internal forces act in the plane of section C and
are called shearing forces

30. Ductility, Brittleness, Toughness, Malleability,
Behaviour of Ferrous & Non-Ferrous metals in Tension
& Compression, Shear & Bending tests, Standard Test
Pieces, Influence of Various Parameters on Test
Results, True & Nominal Stress, Modes of Failure,
Characteristic Stress-Strain Curves, Izod, Charpy &
Tension Impact Tests,
Fatigue, Creep, Corelation between Different
Mechanical Properties, Effect of Temperature, Testing
Machines & Special Features, Different Types of
Extensometers & Compressemeters, Measurement of
Strain by Electrical Resistance Strain Gauges
Mechanical Properties of Materials:-

31. •Strength and stiffness of structures is function of size and
shape, certain physical properties of material.
•Properties of Material:-
• Elasticity
• Plasticity
• Ductility
• Malleability
• Brittleness
• Toughness
• Hardness

32. Material Types
There are many kinds of materials, but most of them can be divided into
four groups:
• Metals - Metals are composed of one or more metallic elements and
often also nonmetallic elements
in relatively small amounts.
• Ceramics - Ceramics are compounds between metallic and nonmetallic
elements.
• Polymers - Most polymers are made up of organic compounds. Polymers
have a very large molecular
structure.
• Composites - A combination of two or more of the above material types
is called a composite
material.

39. INTERNAL FORCE:- STRESS
• Axial Compression
• Shortens the bar
• Crushing
• Buckling
nm
P P
P=
A
• Axial tension
•Stretches the bars &
tends to pull it apart
• Rupture
m n
=P/A
PP

40. • Resistance offered by the material per unit cross-
sectional area is called STRESS.
 = P/A
Unit of Stress:
Pascal = 1 N/m2
kN/m2 , MN/m2 , GN/m2
1 MPa = 1 N/mm2
Permissible stress or allowable stress or working
stress = yield stress or ultimate stress /factor of
safety.

41. Example: 2
A Steel wire hangs vertically under its weight.
What is the greatest length it can have if the
allowable tensile stress t =200 MPa? Density of
steel =80 kN/m3.(ans:-2500 m)
Solution:
t =200 MPa= 200*103 kN/m2 ;
=80 kN/m3.
Wt. of wire P=(/4)*D2*L* 
c/s area of wire A=(/4)*D2
t = P/A
solving above eq. L =2500m
L

42. Example : 1
A short hollow, cast iron cylinder with wall
thickness of 10 mm is to carry compressive load
of 100 kN. Compute the required outside
diameter `D’ , if the working stress in
compression is 80 N/mm2. (D = 49.8 mm).
Solution:  = 80N/mm2;
P= 100 kN = 100*103 N
A =(/4) *{D2 - (D-20)2}
as  = P/A
substituting in above eq. and
solving. D = 49.8 mm
D
d
10 mm

43. Strain
Stress
Stress- Strain Curve for Mild Steel (Ductile Material)
Plastic state
Of material
Elastic State
Of material
Yield stress Point
E = modulus of
elasticity
Ultimate stress
point
Breaking stress
point

44. Modulus of Elasticity:
• Stress required to produce a strain of unity.
• i.e. the stress under which the bar would be
stretched to twice its original length . If the
material remains elastic throughout , such
excessive strain.
• Represents slope of stress-strain line OA.
A


O
stress
strain
Value of E is same
in Tension &
Compression.
 =E 
E

45. Example:4 An aluminium bar 1.8 meters long
has a 25 mm square c/s over 0.6 meters of its
length and 25 mm circular c/s over other 1.2
meters . How much will the bar elongate under
a tensile load P=17500 N, if E = 75000 Mpa.
Solution :-  = ∑PL/AE
=17500*600 / (252*75000) +
17500*1200/(0.785*252*75000) =0.794 mm
0.6 m
1.2 m
25 mm sq.sect25 mm cir..sect
17500 N

46. 15 kN
1 m 1 m 2 m
20 kN 15 kN
Example: 5 A prismatic steel bar having cross
sectional area of A=300 mm2 is subjected to axial
load as shown in figure . Find the net increase  in
the length of the bar. Assume E = 2 x 10 5 MPa.( Ans
 = -0.17mm)
 = 20000*1000/(300*2x10 5)-15000*2000/(300*2 x10 5)
= 0.33 - 0.5 = -0.17 mm (i.e.contraction)
C B A
2020 C
00
B
15 15A
Solution:

47. 9 m
x
5 m
3m
A = 445 mm 2
E = 2 x 10 5
A = 1000 mm 2
E = 1 x 10 5
A B
Example: 6 A rigid bar AB, 9 m long, is supported by two
vertical rods at its end and in a horizontal position under
a load P as shown in figure. Find the position of the load
P so that the bar AB remains horizontal.
P

48. 9 m
x
5 m
3m
A B
P
P(9-x)/9 P(x)/9


49. ``
PP
X
L
d1 d2dx
x
Q. Find extension of tapering circular bar under axial pull for the following data: d1 =
20mm, d2 = 40mm, L = 600mm, E = 200GPa. P = 40kN
L = 4PL/( E d1 d2)
= 4*40,000*600/(π* 200,000*20*40)
= 0.38mm. Ans.

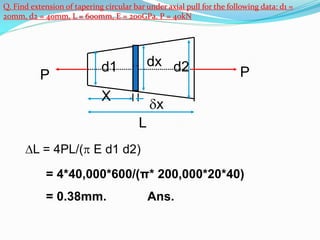
50. PP
X
L
b2 b1bx
x
Take b1 = 200mm, b2 = 100mm, L =
500mm
P = 40kN, and E = 200GPa, t = 20mm
δL= PLloge(b1/b2) / [Et(b1 – b2)]
= 40000*500loge(200/100)/[200000*20 *100]
= 0.03465mm
Q. Calculate extension of Tapering bar of
uniform thickness t, width varies from b1 to
b2:-
P/Et ∫ x / [ (b1 + k*X)],

51. Example: 7 A steel bar having
40mm*40mm*3000mm dimension is subjected to
an axial force of 128 kN. Taking E=2*105N/mm2
and  = 0.3,find out change in dimensions.
Solution:
given b=40 mm,t=40mm,L=3000mm
P=128 kN=128*103 N, E=2*105 mm2,  =0.3
L=?, b=?, t=?
t = P/A = 128*103 /40*40= 80 N/mm2
128 kN128 kN
3000 mm 40
40

52. The displacement per unit length
(dimensionless) is known as strain.
• Tensile strain (εt)
The elongation per unit length as shown
in the figure is known as tensile strain.
εt = ΔL/ Lo

53. Compressive strain (εc)
If the applied force is compressive then the reduction of
length per unit length is known as compressive strain. It
is negative. Then εc = (–ΔL)/ Lo

54. Shear Strain ( γ ):
When a force P is applied tangentially to the element
shown. Its edge displaced to dotted l i n e . Where δ i s t h e l a t e
r a l displacement of the upper face of the
element relative to the lower face and L is the distance between
these faces. Then the shear
strain is (γ) δ/L

55. True stress
 The true stress is defined as the ratio of the load to the
cross section area at any instant
True Strain

56. Poisson’s Ratio (μ)

57. Elongation
A prismatic bar loaded in tension by
an axial force P
For a prismatic bar loaded in tension by
an axial force P. The elongation of the bar
can be determined as

58. Elongation of composite body
Elongation of a bar of varying cross section A1, A2,----------,An of
lengths l1, l2,--------ln respectively.

59. Elongation of a tapered body
Elongation of a tapering rod of length ‘L’ due
to load ‘P’ at the end
(d1 and d2 are the diameters of smaller
& larger ends)
You may remember this in this way,

62. Elongation of a body due to its self weight
Elongation of a uniform rod of length ‘L’ due to its own weight ‘W’
The deformation of a bar under its own weight as compared to that when
subjected to
a direct axial load equal to its own weight will be half.
Total extension produced in rod of length ‘L’ due to its own weight ‘ ω ’ per
with
length.
Elongation of a conical bar due to its self
weight

63. Creep
When a member is subjected to a constant load over a long period of time it
undergoes a slow permanent deformation and this is termed as “creep”. This is
dependent on temperature. Usually at elevated temperatures creep is high.

65. Elasticity
This is the property of a material to regain its original shape after
deformation when the external forces are removed. When the material is
in elastic region the strain disappears completely after removal of the load
Plasticity
When the stress in the material exceeds the elastic limit, the material
enters into plastic phase where the strain can no longer be completely
removed

66. GATE-1. Two identical circular rods of same diameter
and same length are subjected to same magnitude of
axial tensile force. One of the rods is made out of mild
steel having the modulus of elasticity of 206 GPa. The
other rod is made out of cast iron having the modulus
of elasticity of 100 GPa. Assume both the materials to
be homogeneous and isotropic and the axial force
causes the same amount of uniform stress in both the
rods. The stresses developed are within the
proportional limit of the respective materials. Which
of the following observations is correct?
[GATE-2003]
(a) Both rods elongate by the same amount
(b) Mild steel rod elongates more than the cast iron rod
(c) Cast iron rod elongates more than the mild steel rod
(d) As the stresses are equal strains are also equal in both
the rods

67. A steel bar of 40 mm × 40 mm square cross-section is subjected to an axial
compressive load of 200 kN. If the length of the bar is 2 m and E = 200 GPa,
the
elongation of the bar will be: [GATE-2006]
(a) 1.25 mm (b) 2.70 mm (c) 4.05 mm (d) 5.40 mm
The ultimate tensile strength of a material is 400 MPa and the elongation
up to
maximum load is 35%. If the material obeys power law of hardening, then
the
true stress-true strain relation (stress in MPa) in the plastic deformation
range
is: [GATE-2006]
(a) σ = 540ε 0.30 (b) σ = 775ε 0.30 (c) σ = 540ε 0.35 (d) σ = 775ε 0.35
An axial residual compressive stress due to a manufacturing process is
present
on the outer surface of a rotating shaft subjected to bending. Under a given
bending load, the fatigue life of the shaft in the presence of the residual
compressive stress is: [GATE-2008]
(a) Decreased
(b) Increased or decreased, depending on the external bending load
(c) Neither decreased nor increased
(D)Increased

68. A static load is mounted at the centre of a shaft rotating at uniform
angular
velocity. This shaft will be designed for [GATE-2002]
(a) The maximum compressive stress (static) (b) The maximum tensile stress
(static)
(c) The maximum bending moment (static) (d) Fatigue loading
Fatigue strength of a rod subjected to cyclic axial force is less than that
of a
rotating beam of the same dimensions subjected to steady lateral force
because
(a) Axial stiffness is less than bending stiffness [GATE-1992]
(b) Of absence of centrifugal effects in the rod
(c) The number of discontinuities vulnerable to fatigue are more in the rod
(d) At a particular time the rod has only one type of stress whereas the beam
has both
the tensile and compressive stresses.

69. A rod of length L and diameter D is subjected to a tensile load P. Which
of the following is sufficient to calculate the resulting change in
diameter?
(a) Young's modulus (b) Shear modulus [GATE-2008]
(c) Poisson's ratio (d) Both Young's modulus and shear modulus
In terms of Poisson's ratio (μ) the ratio of Young's Modulus (E) to Shear
Modulus (G) of elastic materials is: [GATE-2004]

76. Strain
 When a body is subjected to an external force, there is
some change of dimension in the body. Numerically
the strain is equal to the ratio of change in length to
the original length of the body.
 Strain = Change in length/Original length
 In equation form: e = dL/L
 Units: m/m, mm/m, In/in, in/ft

77. Shear Stress(t) and Shear Strain
 The two equal and opposite forces act tangentially on
any cross sectional plane of the body tending to slide
one part of the body over the other part. The stress
induced is called shear stress and the corresponding
strain is known as shear strain

78.  Elastic Limit
The maximum stress that can be applied to a metal without
producing permanent deformation is known as Elastic Limit
Hooke’s law
This law states that when a material is loaded, within its
elastic limit, the stress is directly proportional to the strain.

80. Yield Point or Yield Stress
 It is the lowest stress in a material at which the
material begins to exhibit plastic properties. Beyond
this point an increase in strain occurs without an
increase in stress which is called Yielding.

81. Ultimate Strength
 It is the maximum stress that a material can withstand
while being stretched or pulled before necking
 Strain Hardening
It is the strengthening of a metal by plastic deformation
because of dislocation(irregular) movements within the
crystal structure of the material. Any material with a
reasonably high melting point such as metals and alloys can
be strengthened by this method.

82. Applications
 In Civil Engineering to design foundations and
structures
 In Geo-Mechanics to model shape of planets, tectonics
and predict earthquakes
 In Mechanical Engineering to design load bearing
components for vehicles, power generation and
transmission

84. Mechanics
the branch of applied mathematics dealing with motion
and forces producing motion
the machinery or working parts of something.
Mecahanism
a system of parts working together in a machine; a piece of
machinery

87. Engineering stress
Comparison

88. stress is a physical quantity that expresses the internal forces that
neighboring particles of a continuous material exert on each other, while
strain is the measure of the deformation of the material. For example, when
a solid vertical bar is supporting a weight, each particle in the bar pushes on the
particles immediately below it. When a liquid is in a closed container
under pressure, each particle gets pushed against by all the surrounding
particles. The container walls and the pressure-inducing surface (such as a
piston) push against them in (Newtonian)reaction. These macroscopic forces
are actually the average of a very large number of intermolecular
forces and collisions between the particles in those molecules.

125. Concentrated or Point Load is a load acting on a
small elemental area. In practice, a load cannot be
assumed to act on a single point just like a contact
made by a sharp needle. However, when a load is
transferred through a roller or a sphere on to the
beam the contact will be through a point. In all other
cases, the load is presumed to act on a small
restricted area of the beam. In general, the
concentrated loads are vertical. In certain cases it
can be inclined, horizontal and act below the beam

126. Bending moment at a section is defined as the algebraic sum of the
moments about the section of all the forces (including the reaction) acting
on the beam, either to the left or to the right of the section.
Shear force at a section in a beam is defined as the algebraic sum of all the
forces including the reactions acting normal to the axis of the beam either
to the left or to the right of the section

127. A Beam is a horizontal structural member which is subjected to transverse loading.
The load-bearing capacity of a beam varies with the type of support. Types of supports
are simply supported or rolled support hinged support or pinned support and fixed
support or rigid support or encastred support.
Simply supported is the simplest support whose reaction is normal to the plane of
the roller or the support.
Pinned support can withstand force in any direction. The reaction is normal to the
plane of the support and in addition it has a horizontal reaction along the axis of the
beam.
Fixed support is the one which prevents the beam not only from rotation but also
linear movement or translation.
Beams are classified according to their ...
The best content

128. When a beam is subjected to a loading system or by a force couple acting on a
plane passing through the axis, then the beam deforms. In simple terms, this
axial deformation is called as bending of a beam (Figure 5.1).

129. Stress is defined as the internal resistance set up by a body
when it is deformed. It is measured in N/m2 and this unit is
specifically called Pascal (Pa). A bigger unit of stress is the
mega Pascal (MPa).
1 Pa = 1N/m2,
1MPa = 106 N/m2 =1N/mm2.
Three Basic Types of Stresses
Basically three different types of stresses can be identified.
These are related to the nature of the deforming force applied
on the body. That is, whether they are tensile, compressive or
shearing.

177. Bi-Axial Stress

178. Tri-Axial