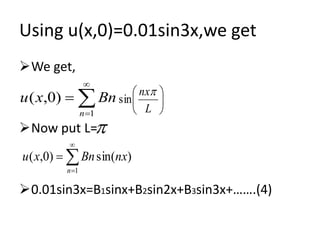This document discusses partial differential equations and provides examples of solving some common types of PDEs. It covers: - The definition of a partial differential equation as a relationship between a dependent variable and two or more independent variables. - Methods for forming and solving first order linear PDEs using Lagrange's method of grouping or multipliers. - The one-dimensional wave equation and heat equation, and methods for solving them given initial conditions or boundary values. - An example of solving the one-dimensional wave equation for an initial deflection of 0.01sinx.

1. G.H.PATEL COLLEGE OF
ENGINEERING&TECH
ADVANCE ENGINEERING MATHEMATICS (2130002)
BY:- uttam trasadiya
Mechanical engineering
GCET college
vvnagar

2. PARTIAL DIFFERENTIAL EQUATIONS
• The relationship between a
dependent variable and two or more
independent variables and partial
differential coefficients of a
dependent variable with respect to
these independent variables is called
as a partial differential equation.

3. FORMATION OF PDEs
• A PDEs can be formed in Two
ways:
By eliminating arbitrary
constants from the given
relation .
By eliminating arbitrary
functions from the given
relation .

4. FIRST ORDER LINEAR PDEs
• A PDE of the form ;
P p + Q q = R
• Where P,Q,R are functions of
x,y,z or constant is called the
Lagrange's linear equation of
first order.

5. LAGRANGE’S METHOD
GROUPING METHOD:
 In this method ,we compare any two fractions
which makes the integration possible.
MULTIPLIERS METHOD:
 In this method ,we find two sets of multipliers
l,m,n and l’,m’,n’ such that;
lP+mQ+nR=0 and l’P+m’Q+n’R=0
From auxiliary equations dx/P=dy/Q=dz/R
It can be solved using the grouping or multiplier
method.Solution denoted by u(x,y)=c,v(x,y)=c’
Complete solution write as F(u,v)=0

6. FIRST ORDER NON - LINEAR PDEs
• A partial differential equation of order one
which is not linear is called a non linear partial
differential equation of first order.
• There are four forms of the FIRST ORDER NON -
LINEAR PDEs.
 General form :f(x,y,z,p,q)=0
I. F(p,q)=0
II. F(z,p,q)=0
III. F(x,p)=G(y,q)
IV. Z=px+qy+F(p,q)

7. LINEAR PDEs WITH CONSTANT
COEFFICIENTS
 Homogeneous linear PDEs:
 If the order of all partial derivatives involved
in linear PDE are same ,then the equation
called a homogeneous linear PDE.
 Non homogeneous linear PDEs:
 If the order of all partial derivatives involved
in linear PDE are distinct ,then the equation
called Non homogeneous linear PDE.

8. ONE DIMENSIONAL WAVE EQUATION
• Where u(x,t) is deflection of string.
The wave equation is mainly used to
determined the motion of vibrating string.
if the initial deflection u(x,0) is f(x) and initial
velocity is g(x),then the solution of wave
equation is given by


















 

 L
nx
L
ctn
Bn
L
ctn
Bntxu
n

sin]sin*cos[),(
1
2
2
2
2
2
x
u
c
t
u





)0,(x
t
u



9. ONE DIMENSIONAL HEAT EQUATION
• The one dimensional heat equation is given by
where
• here (x,t ) is the temperature , is the thermal
diffusivity ,k the thermal conductivity , the
specific heat and the density of the material of
the body.
• It is mainly used to determine the conduction of
heat in wires or bars .

k
c 2
2
c


k
c 2

10. SOLUTION OF HEAT EQUATION
• If the ends are kept at temperature 0*c or the
boundary condition are u(0,t)=u(L,t)=0,then the
solution of the heat equation is given by
• If the ends are insulated or the boundary
conditions are
then solution of the heat equation is given by
t
L
cn
n
e
L
xn
Bntxu
2
222
sin),(
1

 







 
0),(),0( 





tL
x
u
t
x
u











1
2
cos),(
n
t
L
cn
e
L
xn
AnAotxu



11. EXAMPLE:
Find u(x,t) of the string of length L= when
=1 the initial velocity is zero, and the
initial deflection is 0.01sinx.
The deflection u(x,t) is given by the wave
equation,
………….(1)
Length= ,initial velocity=g(x)=0 …..(2)
2
c
2
2
2
2
2
x
u
c
t
u





  x0


12. We know that,
u(0,t)=u( ,t)=0 for all
u(x,0)=0.01sin3x
We know that the solution of (1) together
with (2) is given by………
Here g(x)=0 so , Bn*=0
…..(3)
 0t
 x0


















 

 L
nx
L
ctn
Bn
L
ctn
Bntxu
n

sin]sin*cos[),(
1






 

 L
ctn
Bntxu
n

cos),(
1






L
nx
sin

13. Using u(x,0)=0.01sin3x,we get
We get,
Now put L=
0.01sin3x=B1sinx+B2sin2x+B3sin3x+…….(4)






L
nx
sin



1
)0,(
n
Bnxu

)sin()0,(
1
nxBnxu
n





14. From equation (4) we get,
By equating terms,
B3=0.01, Bn=0…… where n 3
Thus equation (3) becomes,
Here c=1 ; so by putting value of c in equation (5)
 we get general solution of deflection,







 

 L
ctn
Bntxu
n

cos),(
1






L
nx
sin
)5......(cos3sin01.0 ctx
.cos3sin01.0 tx),( txu

15. THANK YOU…..