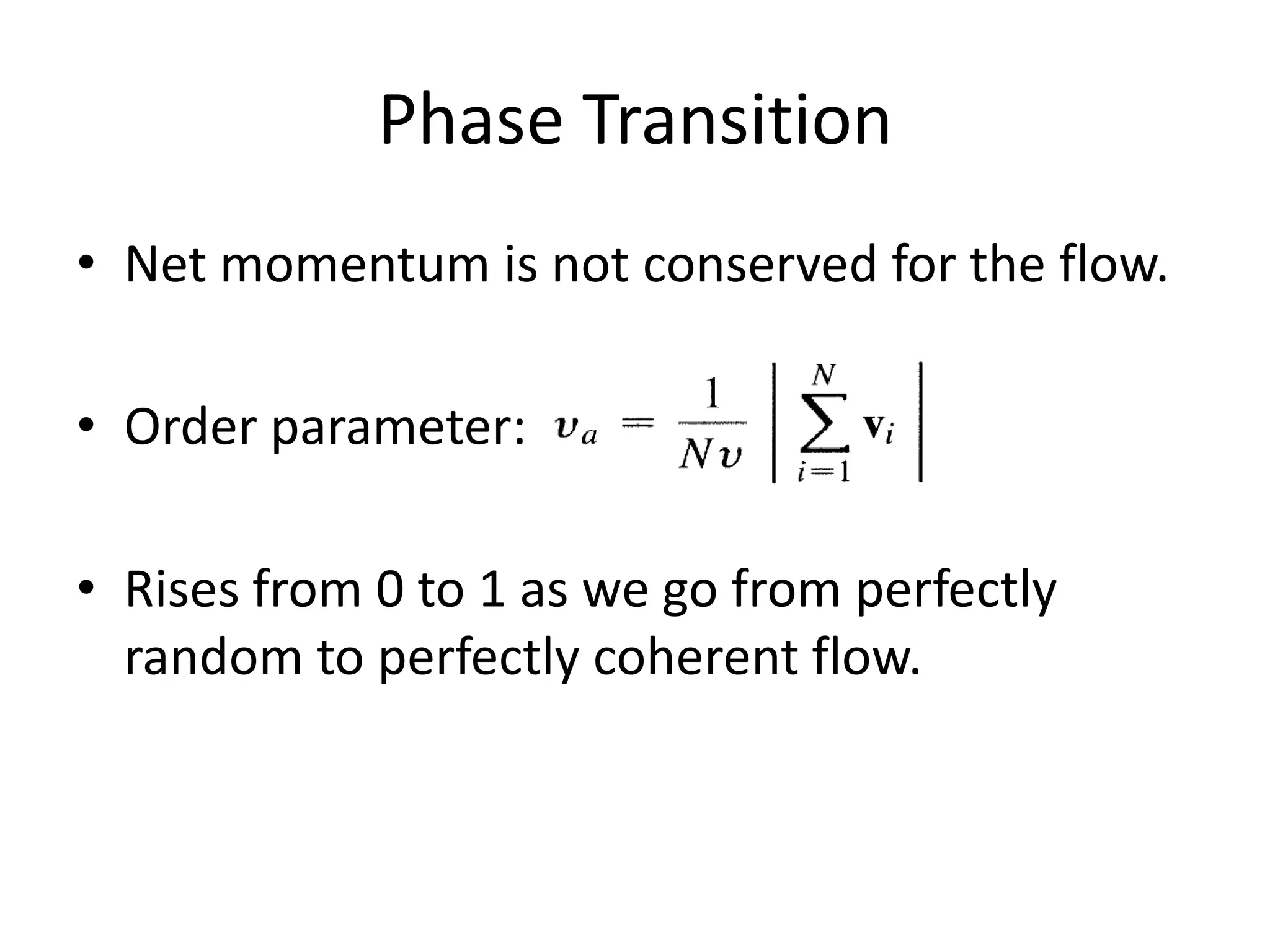
Active matter consists of active units that take in and dissipate energy, often leading to large-scale organization. Examples include cytoskeleton with molecular motors and schools of fish. The Vicsek model simulates flocking through particles that maintain a fixed speed but align their direction of motion based on nearby particles, with some random perturbation. It exhibits a phase transition from disorder to global coherence as noise is reduced. While simple, it demonstrates self-organization in self-driven systems and similarities to models of magnetism. However, it is a minimal model that requires more biological realism and tuning of parameters like neighborhood size.

2. What is Active Matter?
• As opposed to passive matter, it is any system consisting of
active units with the capability of taking in, employing and
dissipating energy.
• These often lead to large scale organization.
• They can be considered as a state of matter and some
condensed matter theory and statistics can be applied to
them.
• Examples: cytoskeleton with molecular motors, schools of
fish, flocks of birds.

3. Criteria for Active Matter
1. The energy input takes place directly at the scale of
each active particle, and is thus homogeneously
distributed through the bulk of the system, unlike
bulk fluids or matter where energy is applied at the
boundaries.
2. Self-propelled motion is force-free: the forces that
particle and fluid exert on each other cancel.
3. The direction of self-propelled motion is set by the
orientation of the particle itself, not fixed by an
external field.

4. Flocking: The Vicsek Model
Vicsek et al, PRL 1995.
• Flock of moving particles. Continuous in space, discrete in time.
• Every particle has the same fixed speed but different directions of
motion.
• At each time step a particle assumes the average direction of
motion of the particles in its neighborhood of radius r.
• Some random perturbation added to this alignment.
• Does this satisfy all criteria of active matter?

5. Vicsek Model: some more specifics
• Starts with random density and directions and
periodic boundary conditions.
• At every time step, the positions are updated:
• And the directions of motion:
• Statistically, the flow is continuous in space.
• Parameters: η, v (0.003 – 0.3), ρ = N/L2.

6. Simulation (N=300, v=0.03)
L=7, η=2.0, t=0 L=25, η=0.1
after some time L=5, η=0.1

7. Von-Mises Distribution of Velocity
• It is the distribution of a drift-diffusion system on
a circle with a harmonic potential.
• Parameters: mean velocity direction and density.

8. Phase Transition
• Net momentum is not conserved for the flow.
• Order parameter:
• Rises from 0 to 1 as we go from perfectly
random to perfectly coherent flow.

9. Change of
Order Parameter
• Fixed density: reaches 1
with lowering η
(chessboard problem).
• Fixed noise: does not
reach 1.

10. Analogy with a Ferromagnetism model
• Similar tendency to locally align spins in the
same direction.
• Random part of alignment can be connected
to thermal noise.
• The difference is the motion in the case of the
flock: equilibrium in ferromagnetism is a static
uniform alignment, for the flock it is a fixed
and uniform direction of flow for all particles.

11. Advantages of the Vicsek Model
• One of the simplest models of a self-driven
system showing cooperative behaviour.
• Although self-driven systems are unusual in
Physics, they are common in living systems.
• Transitions have been observed in traffic models
(cars are self-driven units)
• Behaviour of the order parameter suggests that
theoretical methods for equilibrium critical
phenomena can be applied to self-propelled far-
from-equilibrium systems

12. Limitations of the Vicsek Model
Analysis
• It is too minimalistic to model complex living
systems and requires more control terms.
• Does not explain how living units effect the
averaging that is key to the working of the
model.
• The averaging neighbourhood radius R has not
been tuned (traffic model). This might affect
the range of observed cooperative flow and
thus the order parameter.

13. References
• The Mechanics and Statistics of Active Matter
Sriram Ramaswamy, arXiv 1004.1993v1
• Novel Type of Phase Transition in a System of
Self-Driven Particles
Vicsek et al, Phys. Rev. L. 1995 v 75 no 6
• Webpage of Pierre Degond: Self-Organized
Hydrodynamics