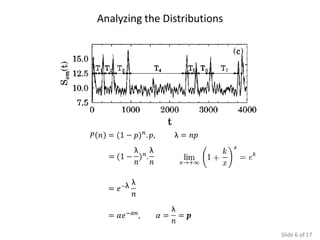
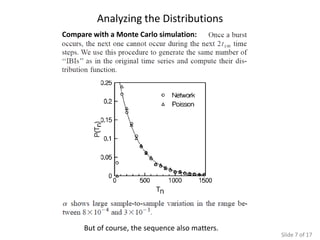
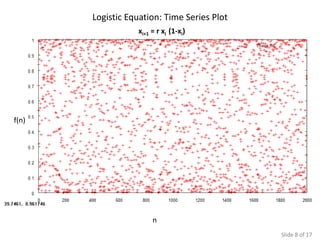
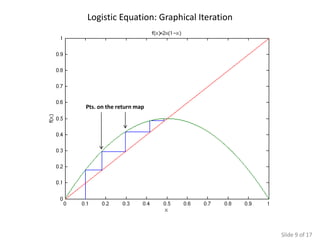
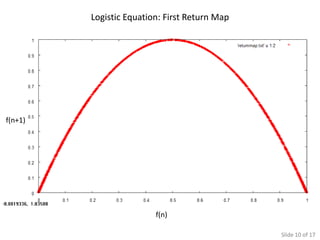
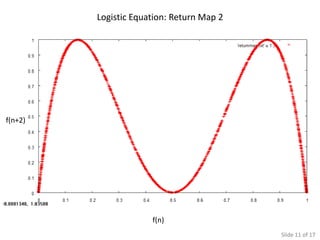
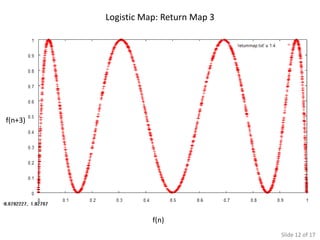
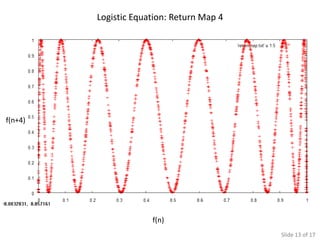
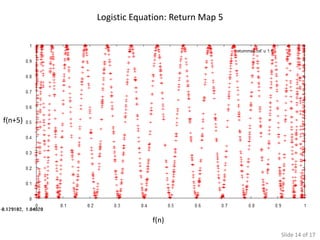
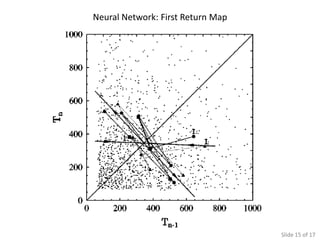
The document presents various simulations and analyses related to logistic equations and chaotic systems, highlighting time evolution, return maps, and the significance of initial conditions. It compares findings with Monte Carlo simulations and discusses determinants of chaos. It also lists multiple sources for further reading on the subject matter.

2. Slide 2 of 17

3. My MATLAB Simulation Data
Slide 3 of 17

4. My MATLAB Simulation Data
Slide 4 of 17

5. Time evolution of the overlaps:
3 0 0 1 0
3 0 0 1 0
3 0 0 1 0
3 0 0 1 0
3 0 0 1 0
3 0 0 1 0
0 3 1 0 1
0 3 1 0 1
0 3 1 0 1
0 3 1 0 1
0 3 1 0 1
0 3 1 0 1
0 1 3 0 0
0 1 3 0 0
0 1 3 0 0
0 1 3 0 0
0 1 3 0 0
0 1 3 0 0
1 0 0 3 0
1 0 0 3 0
1 0 0 3 0
1 0 0 3 0
1 0 0 3 0
1 0 0 3 0
0 1 0 0 3
0 1 0 0 3
0 1 0 0 3
0 1 0 0 3
0 1 0 0 3
0 1 0 0 3
3 0 0 1 0
3 0 0 1 0
3 0 0 1 0
3 0 0 1 0
3 0 0 1 0
3 0 0 1 0 Slide 5 of 17

6. Analyzing the Distributions
Slide 6 of 17

7. Analyzing the Distributions
Compare with a Monte Carlo simulation:
But of course, the sequence also matters.
Slide 7 of 17

8. Logistic Equation: Time Series Plot
xi+1 = r xi (1-xi)
f(n)
n
Slide 8 of 17

9. Logistic Equation: Graphical Iteration
Pts. on the return map
Slide 9 of 17

10. Logistic Equation: First Return Map
f(n+1)
f(n)
Slide 10 of 17

11. Logistic Equation: Return Map 2
f(n+2)
f(n)
Slide 11 of 17

12. Logistic Map: Return Map 3
f(n+3)
f(n)
Slide 12 of 17

13. Logistic Equation: Return Map 4
f(n+4)
f(n)
Slide 13 of 17

14. Logistic Equation: Return Map 5
f(n+5)
f(n)
Slide 14 of 17

15. Neural Network: First Return Map
Slide 15 of 17

16. Determinants of Chaos
• Autocorrelation function
• Return map
• Sensitive dependence on initial conditions
• Unstable Periodic Orbits
• Response to Chaos Control and Anticontrol
Slide 16 of 17

17. Sources
Physical Review E
pre.aps.org
Nature
nature.com
Chaos: the making of a new science
James Gleick
Python programming language
python.org
MATLAB® computing language
mathworks.in/products/matlab
Univ. of Yale online resources on chaos
classes.yale.edu/fractals/chaos/welcome.html
California State Univ. East Bay Hayward Statistics Dept. online resources
sci.csueastbay.edu/statistics/Resources/Essays/PoisExp.htm
Slide 17 of 17