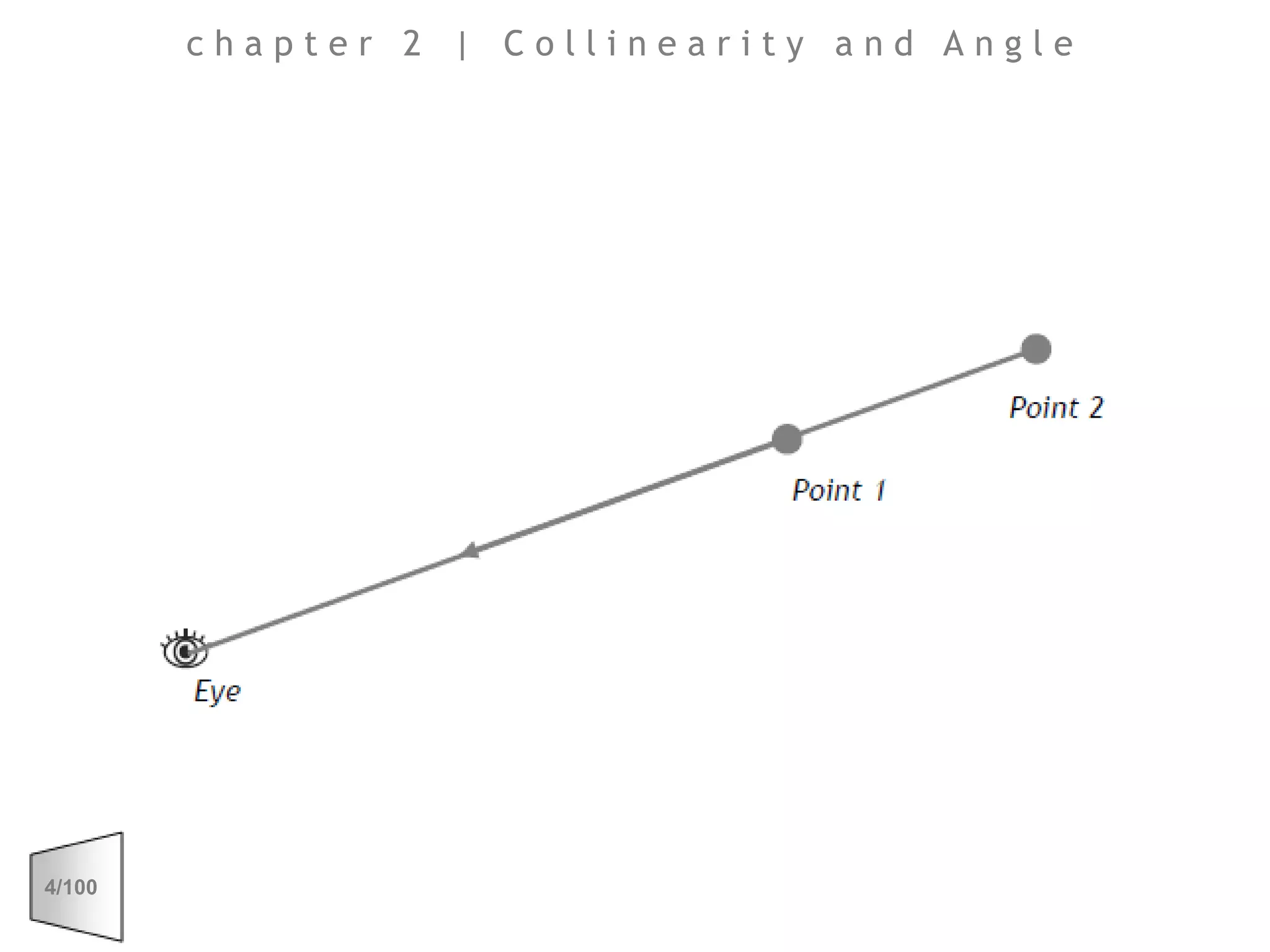
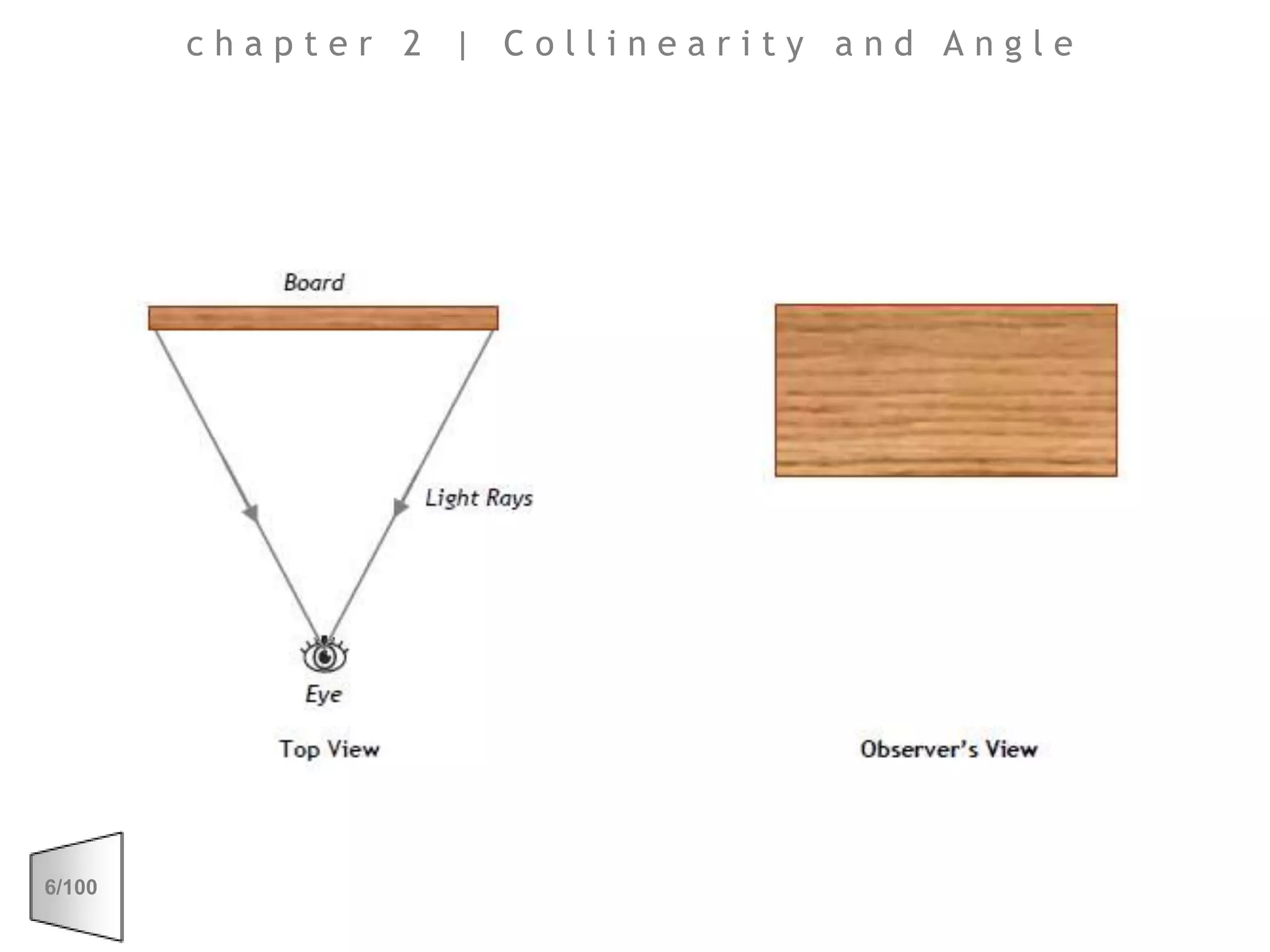
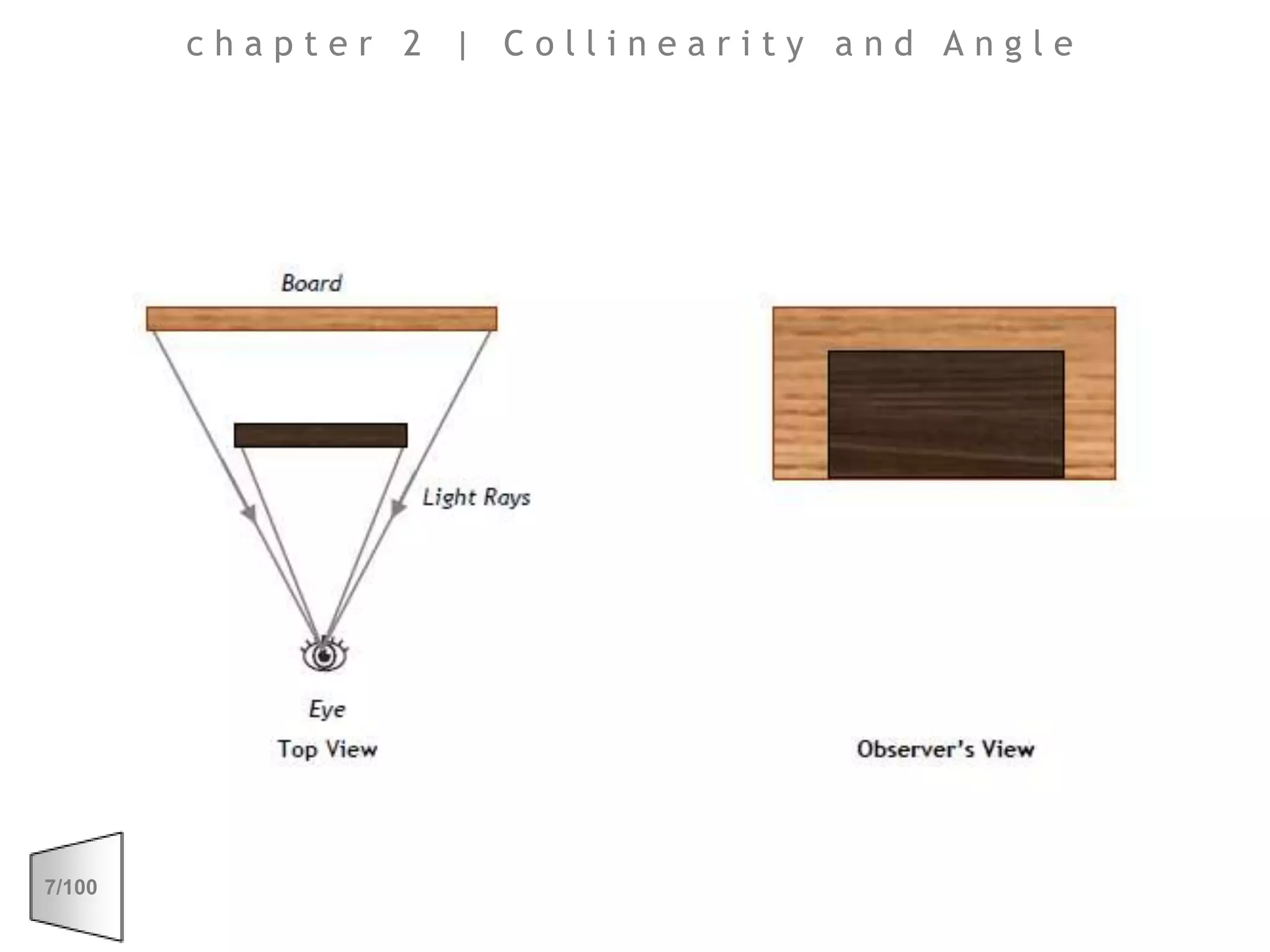
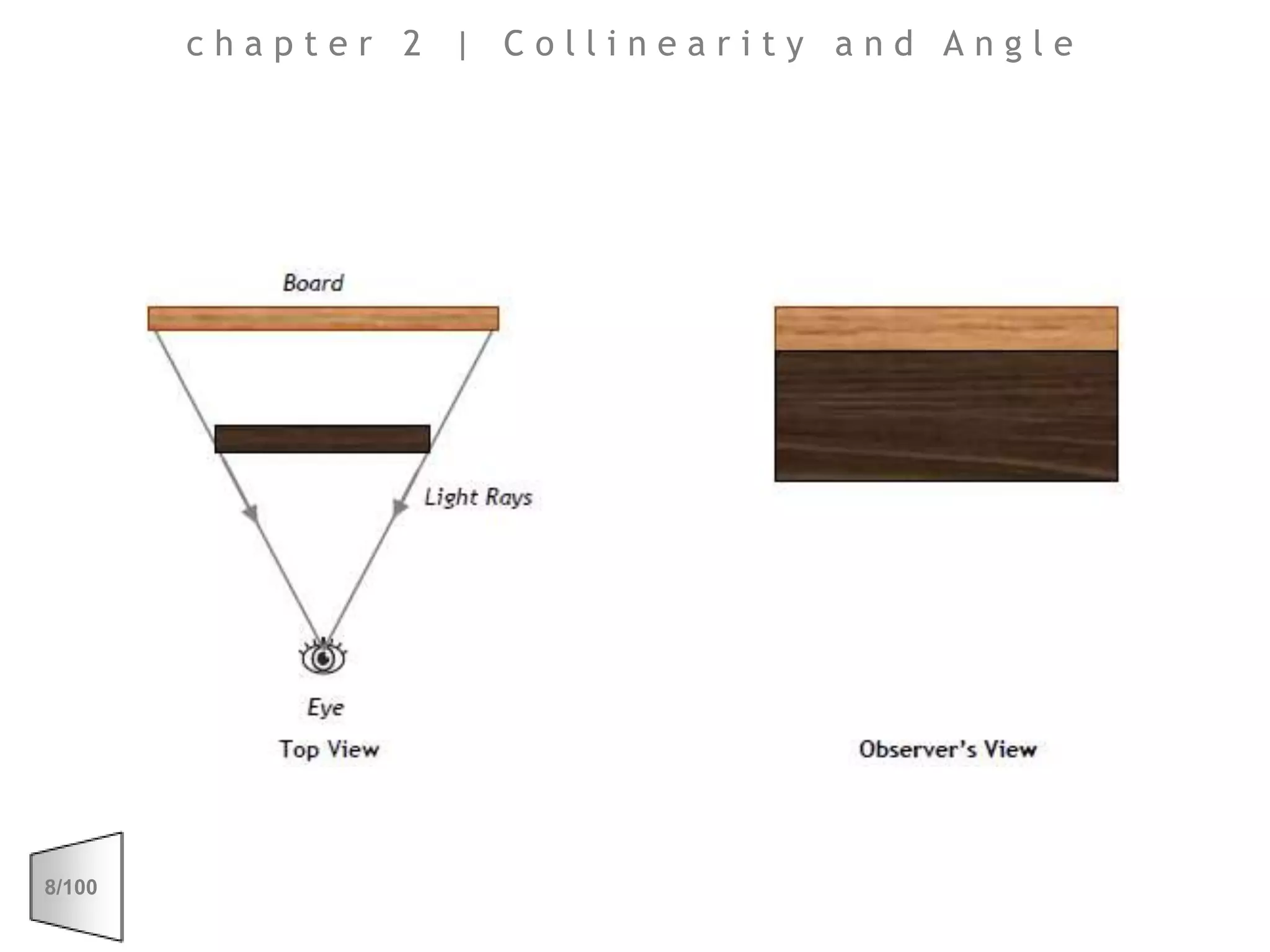
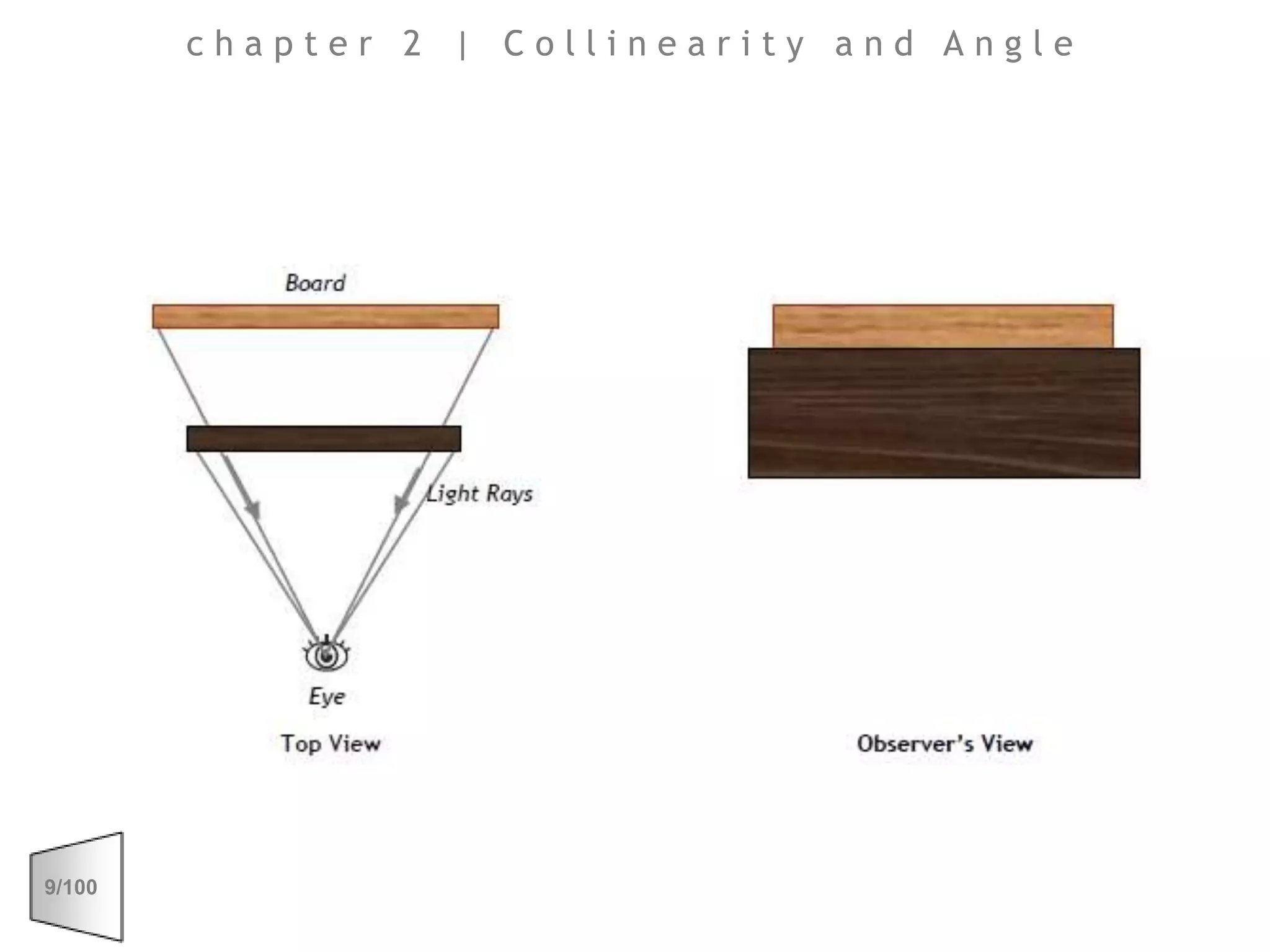
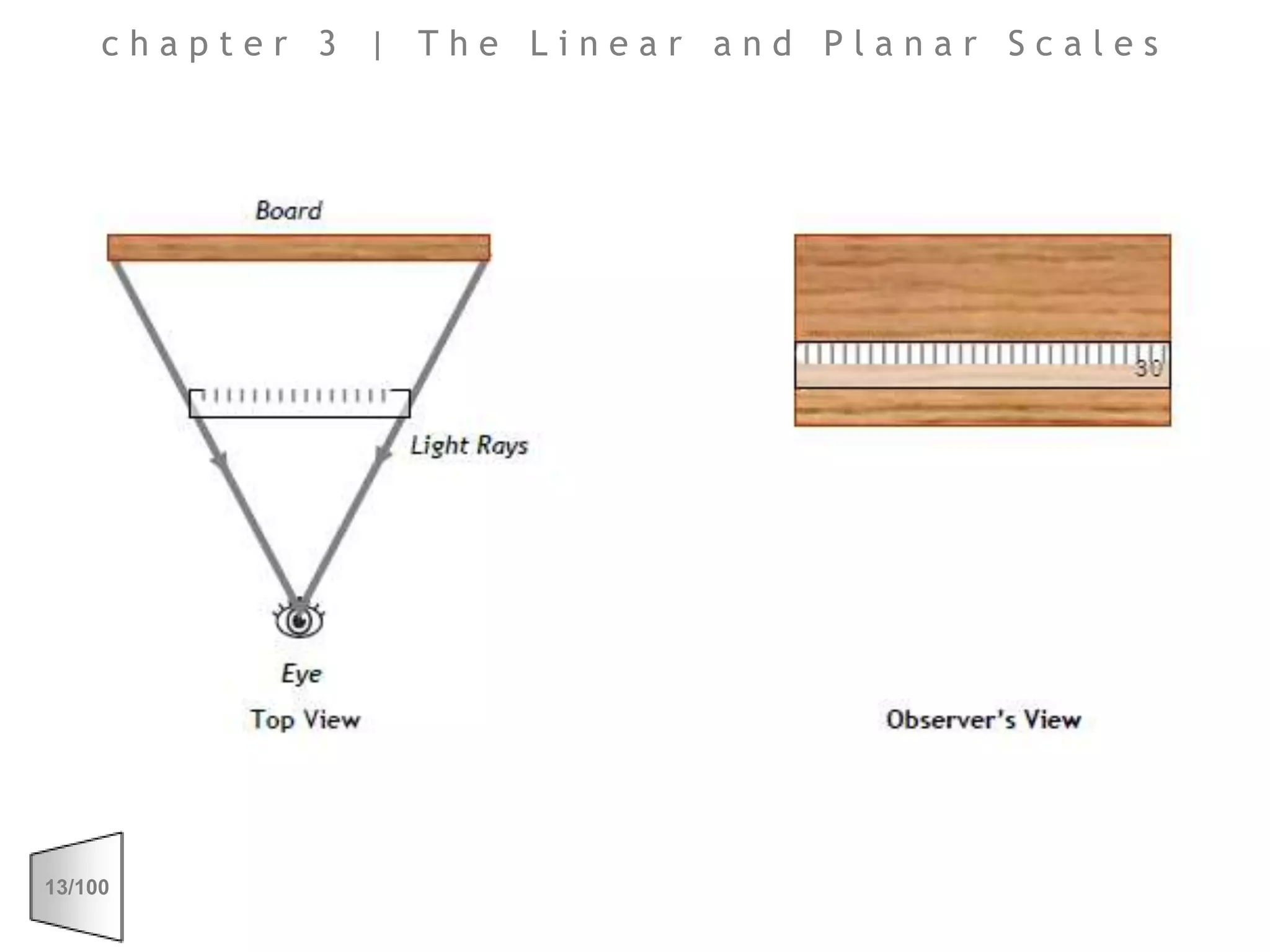
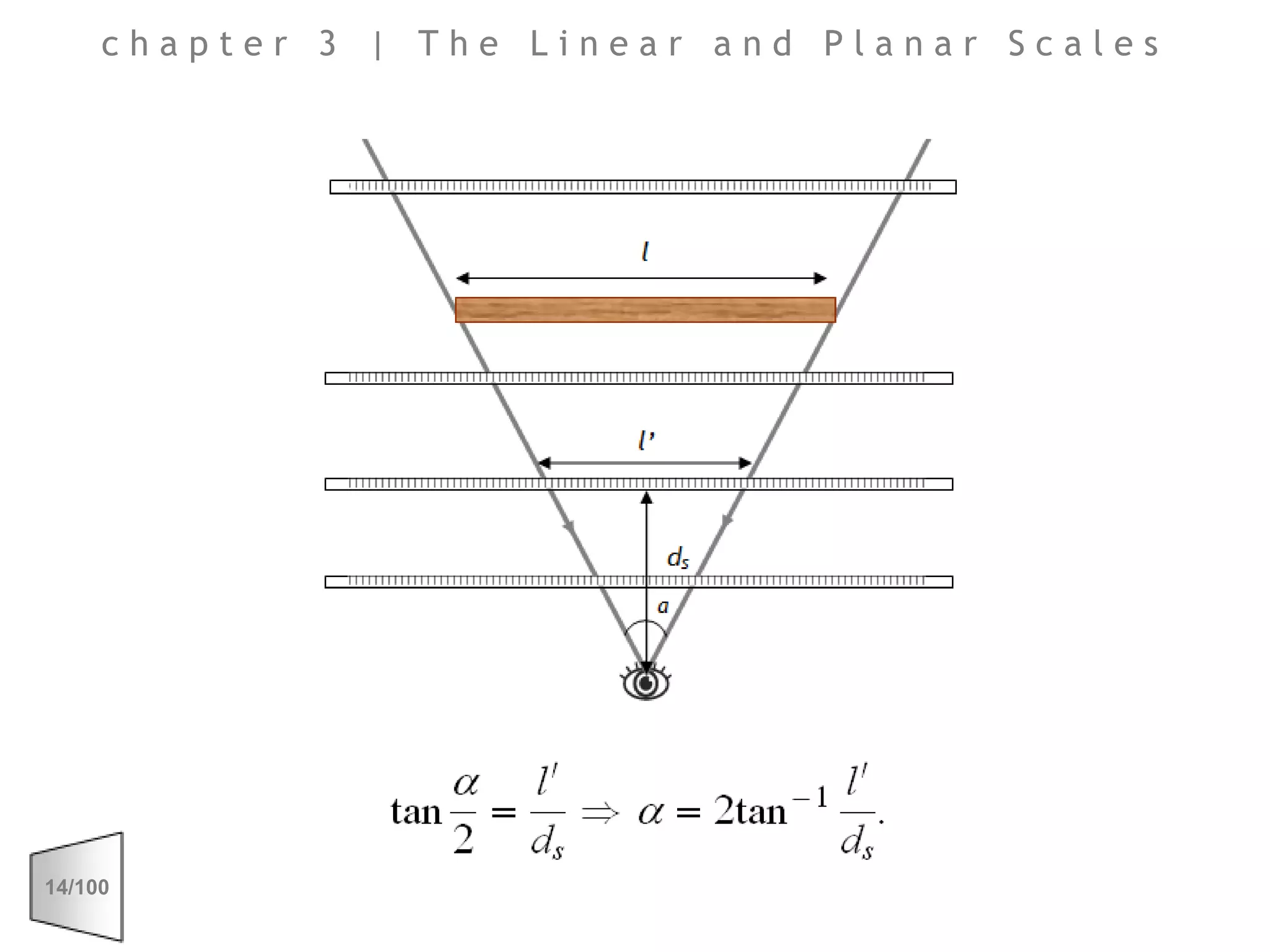
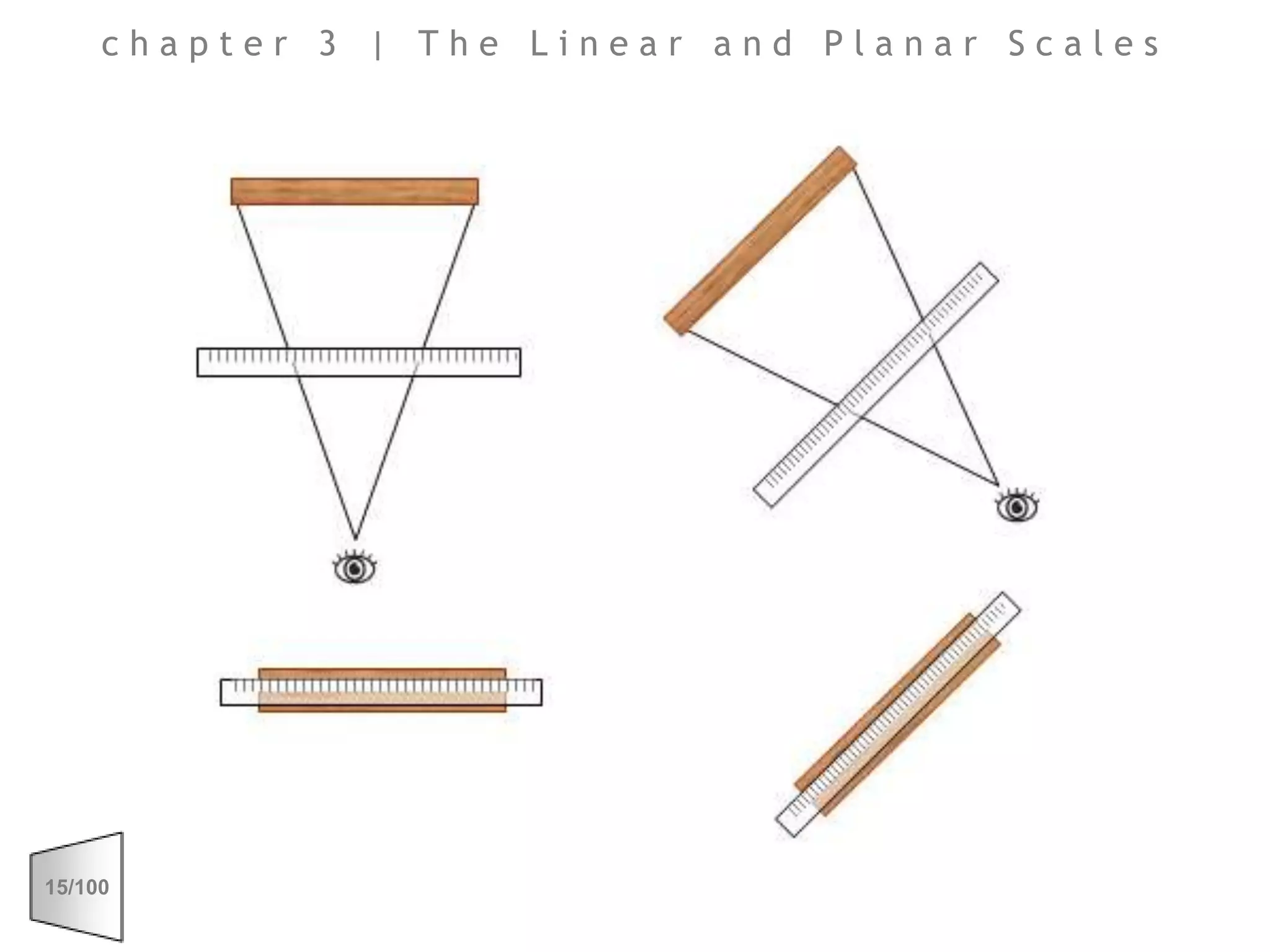
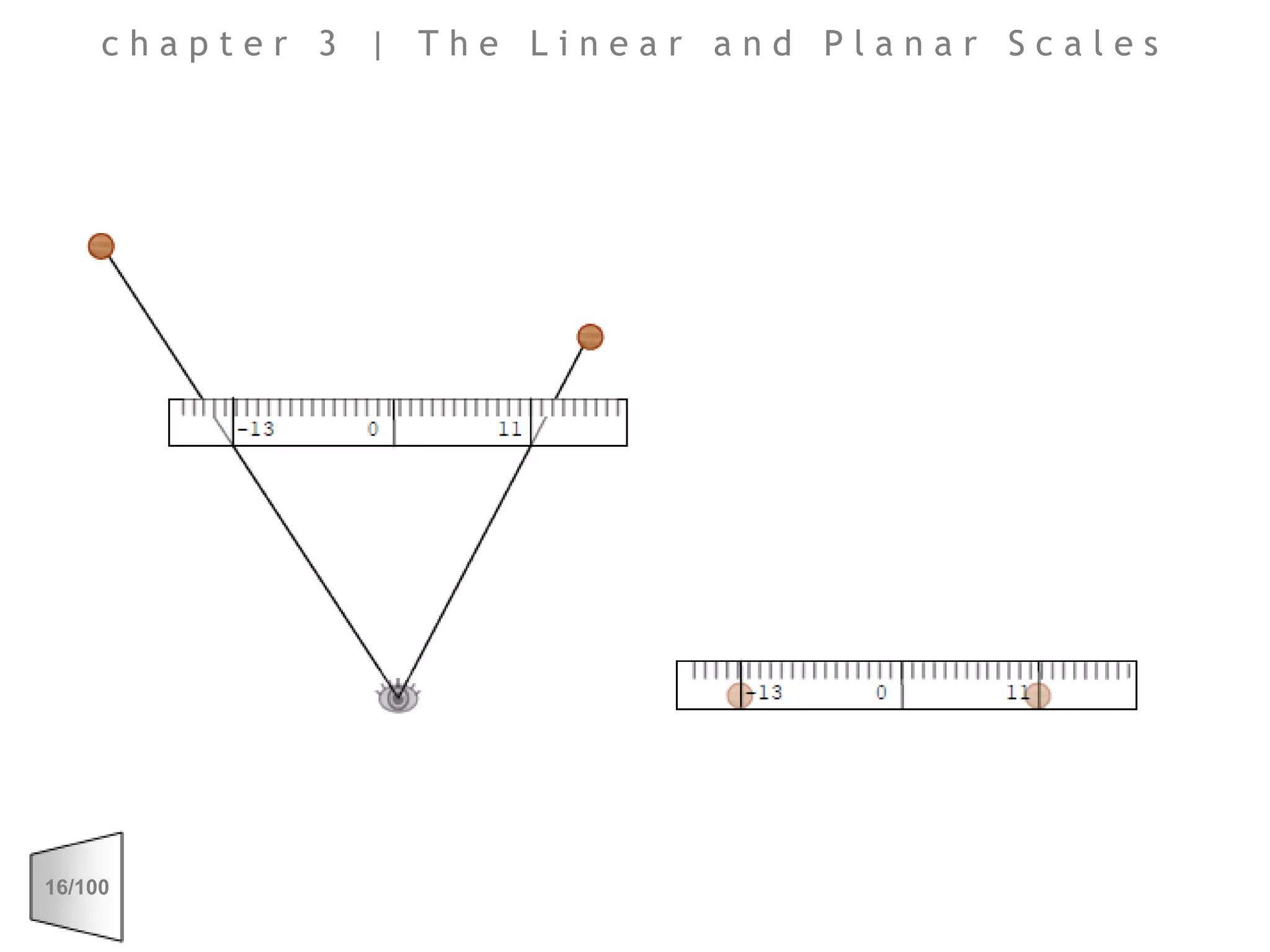
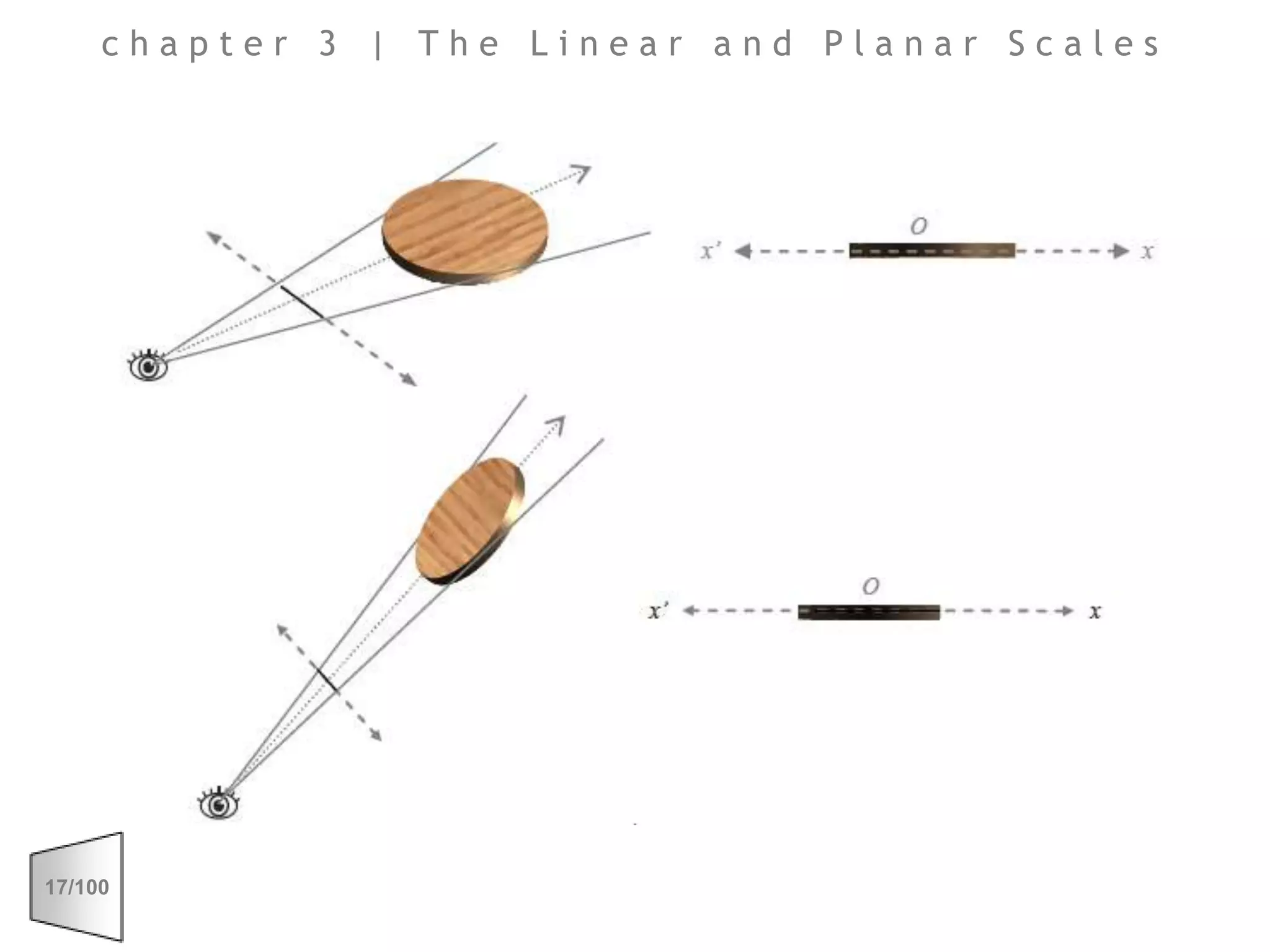
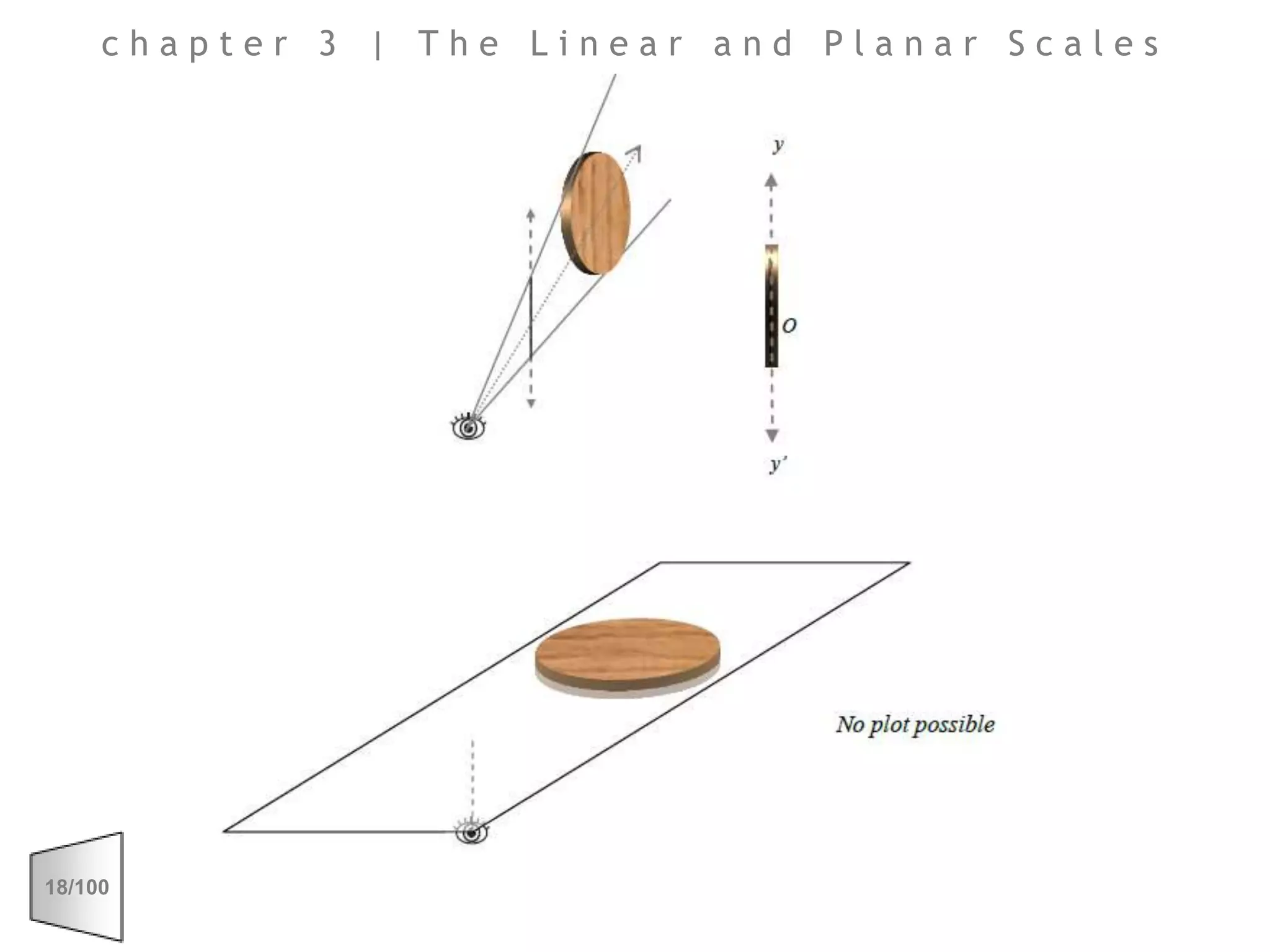
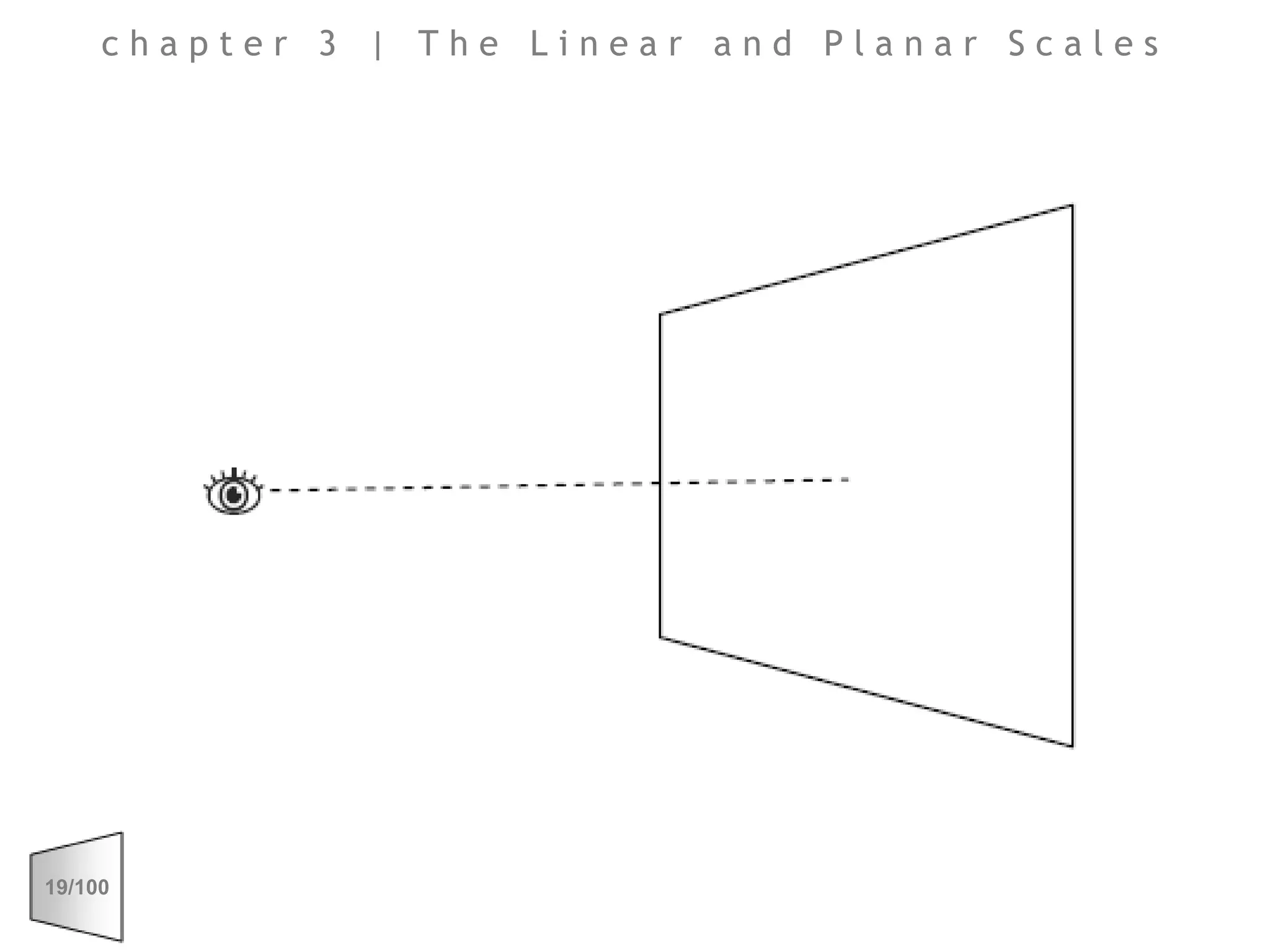
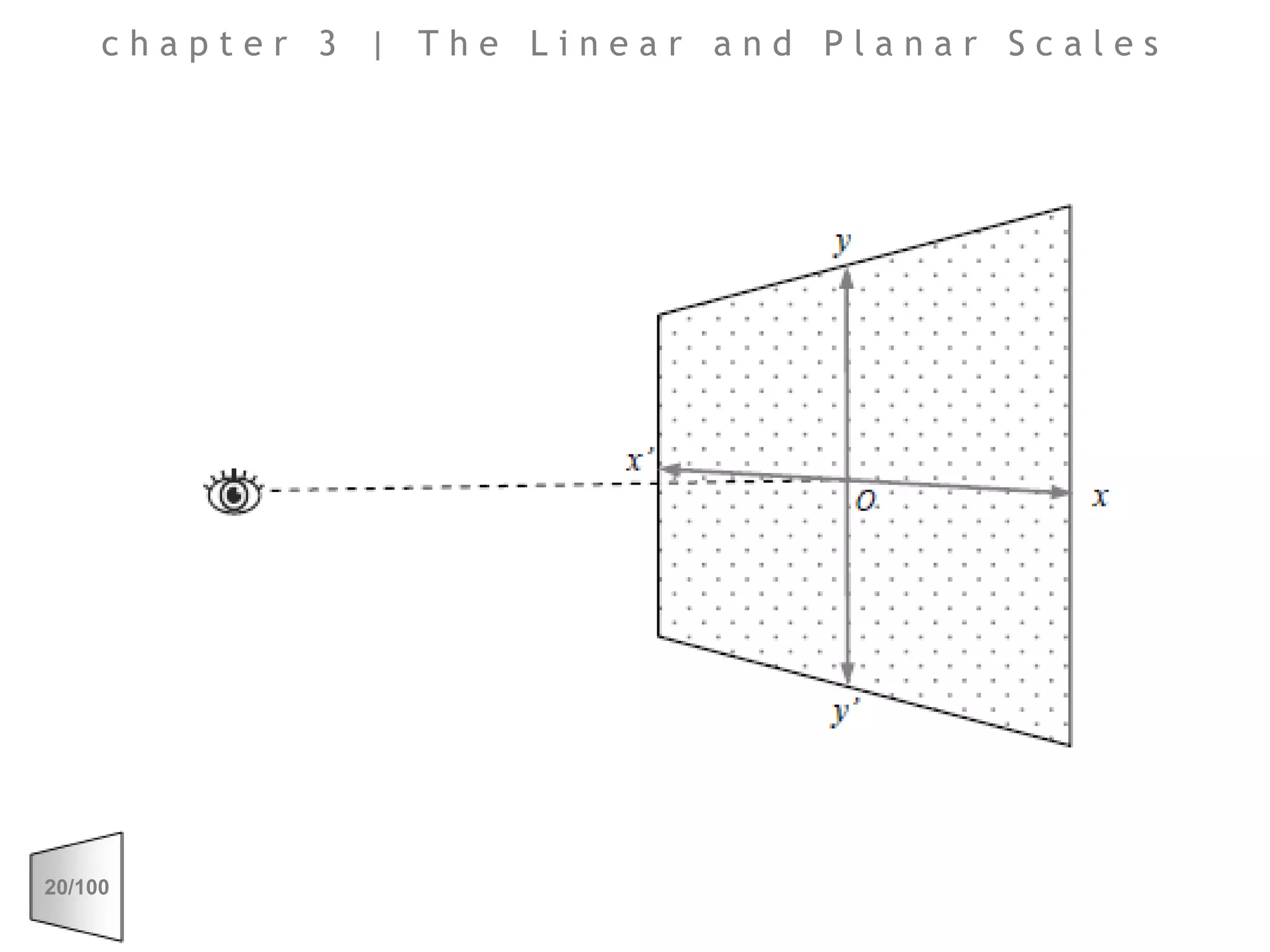
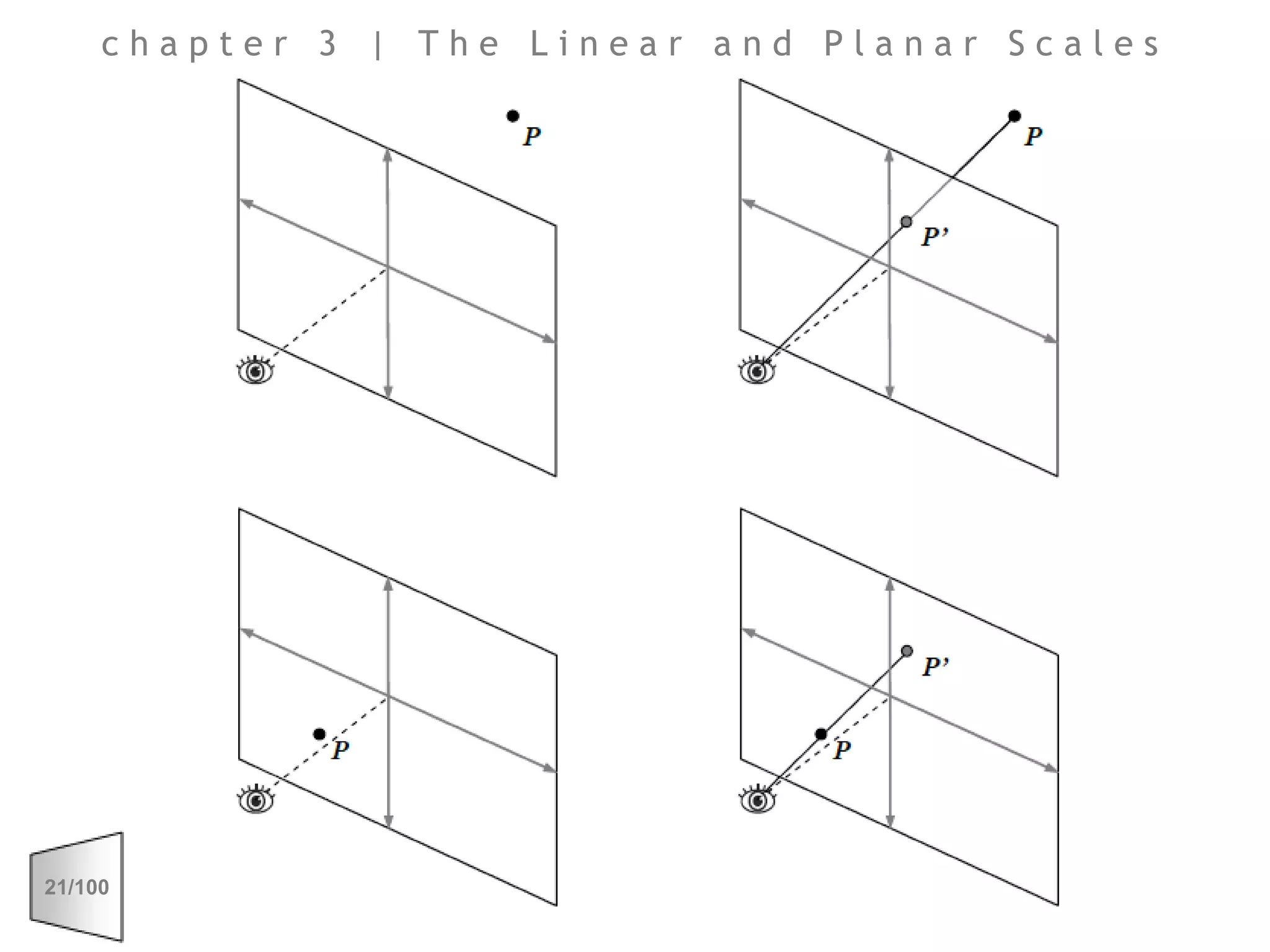
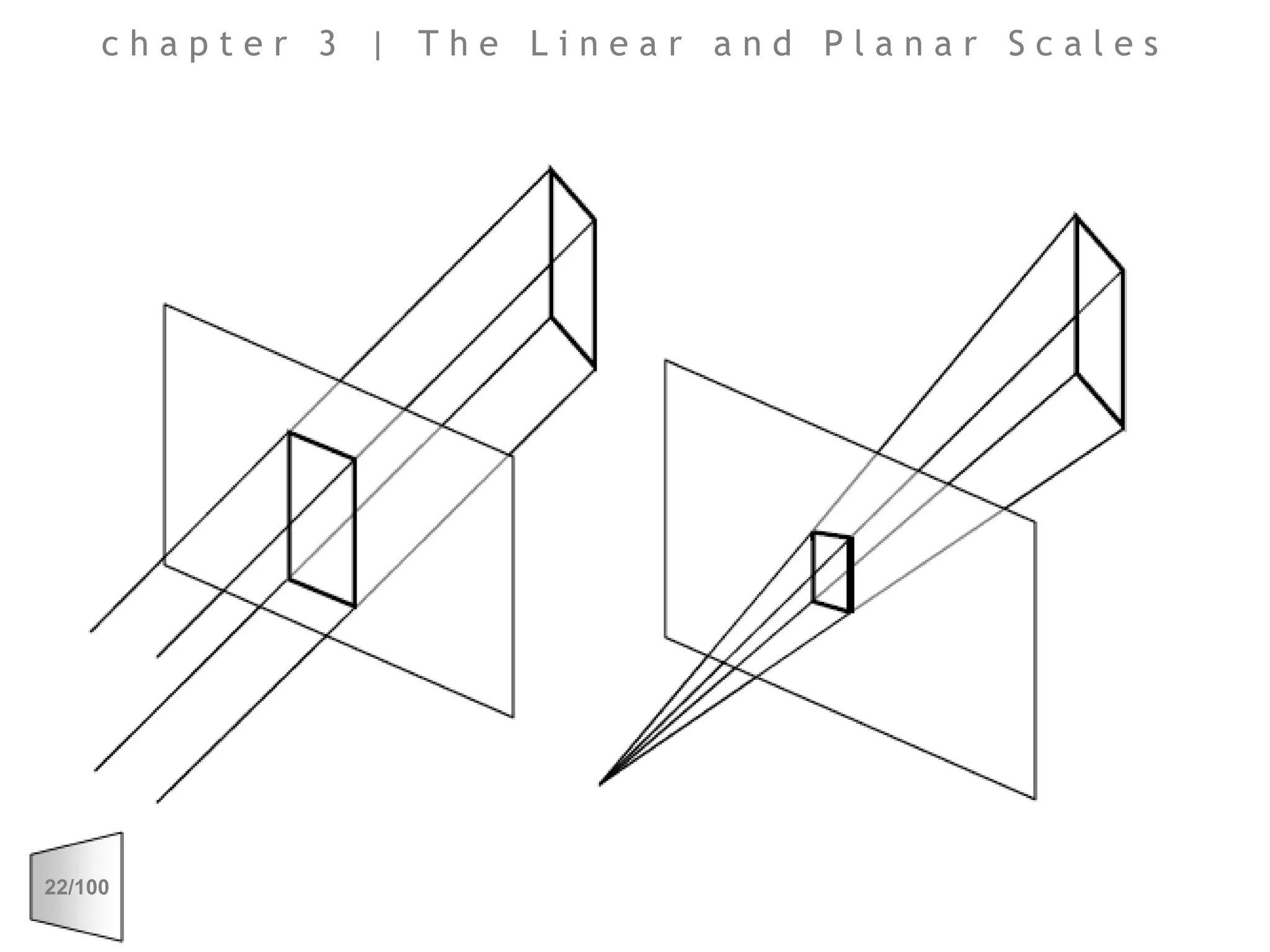
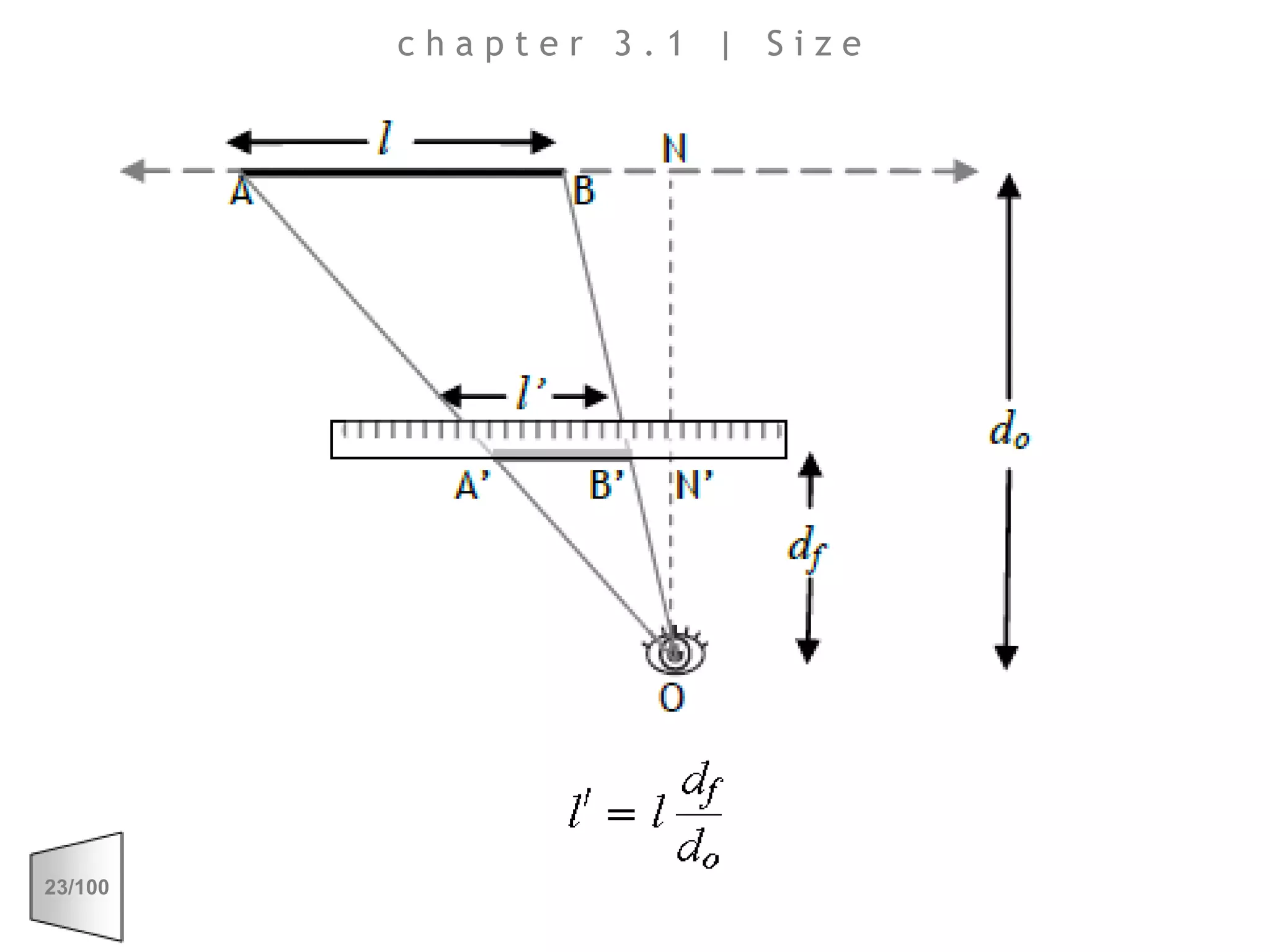
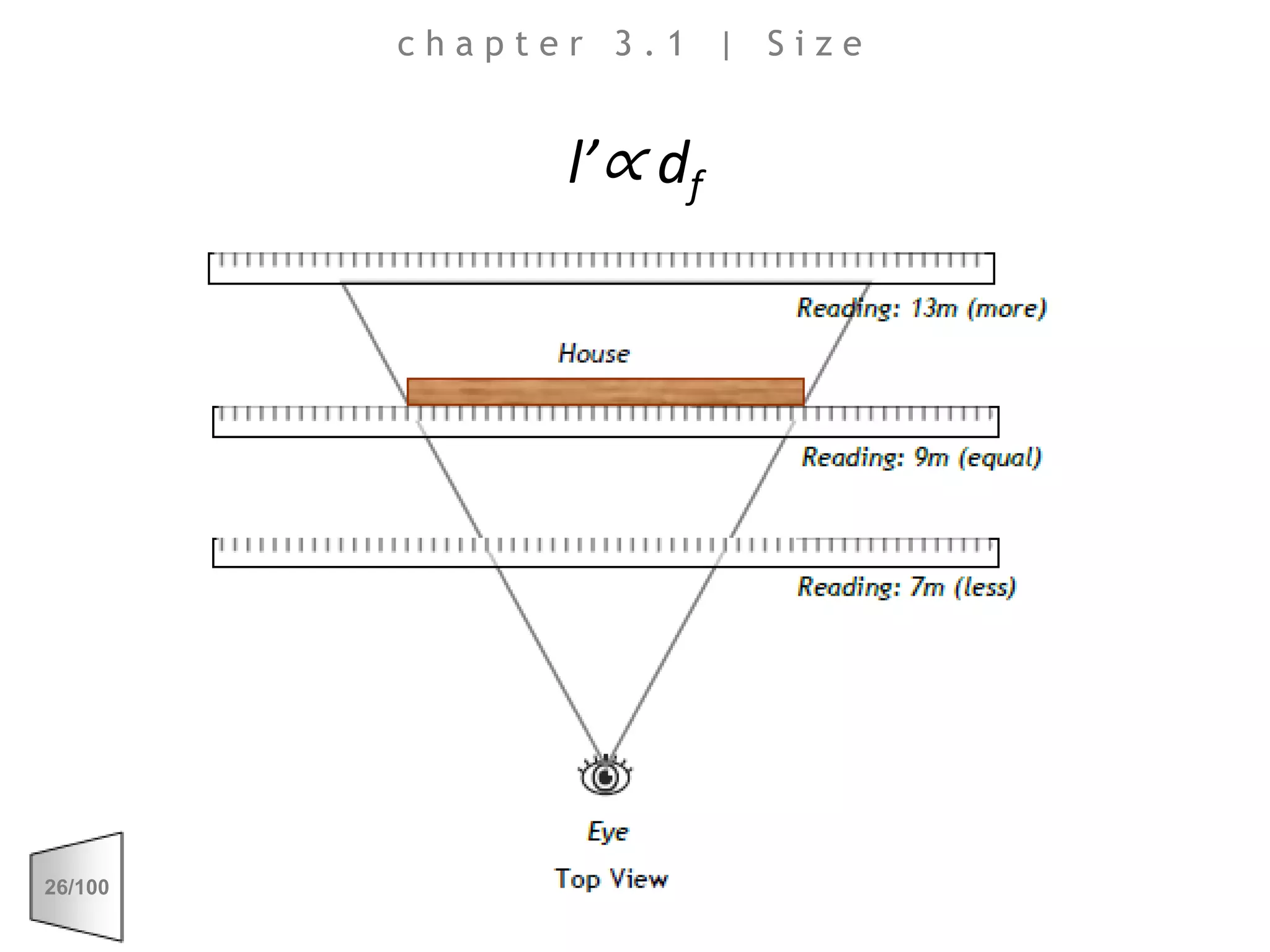
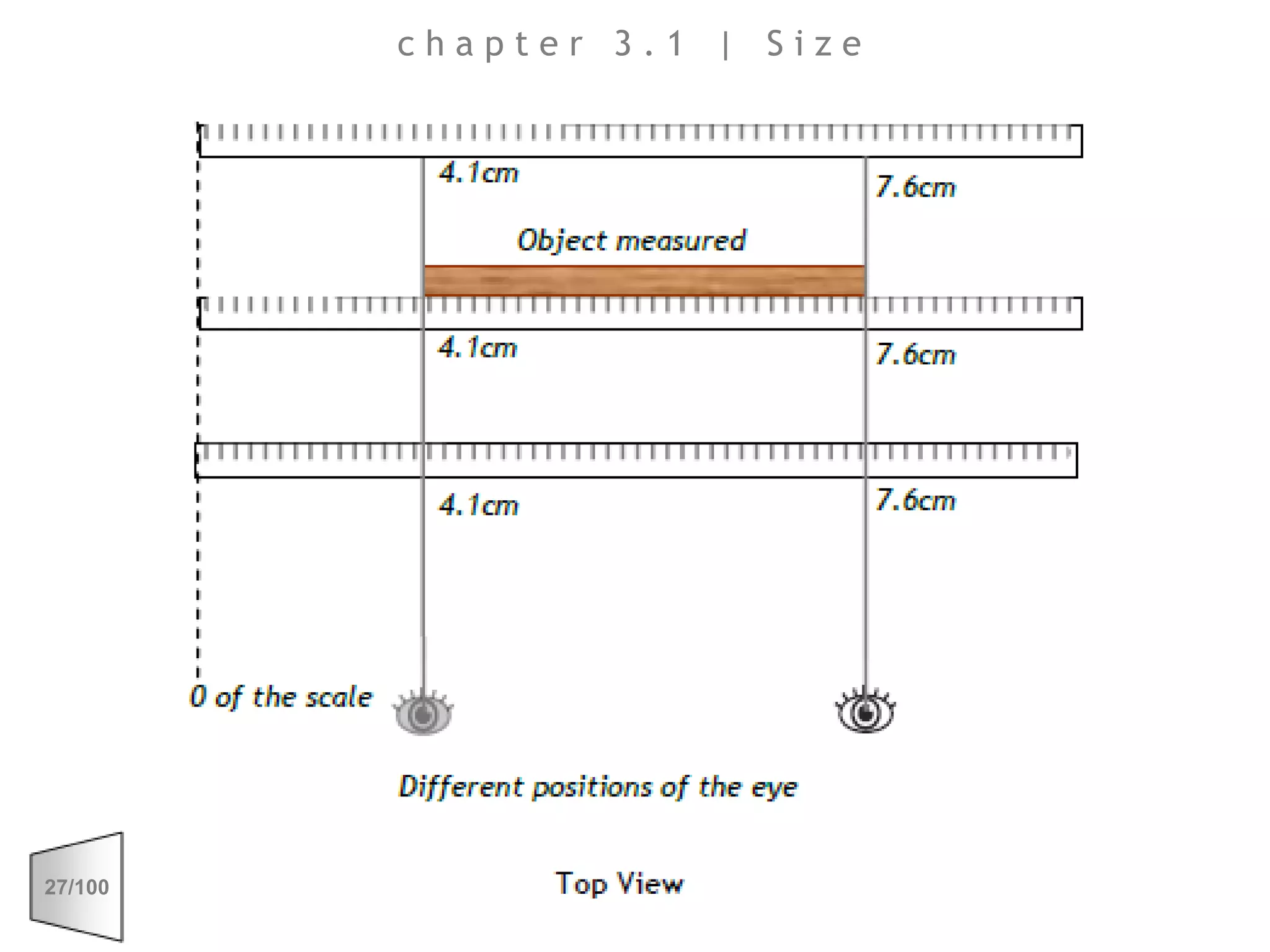
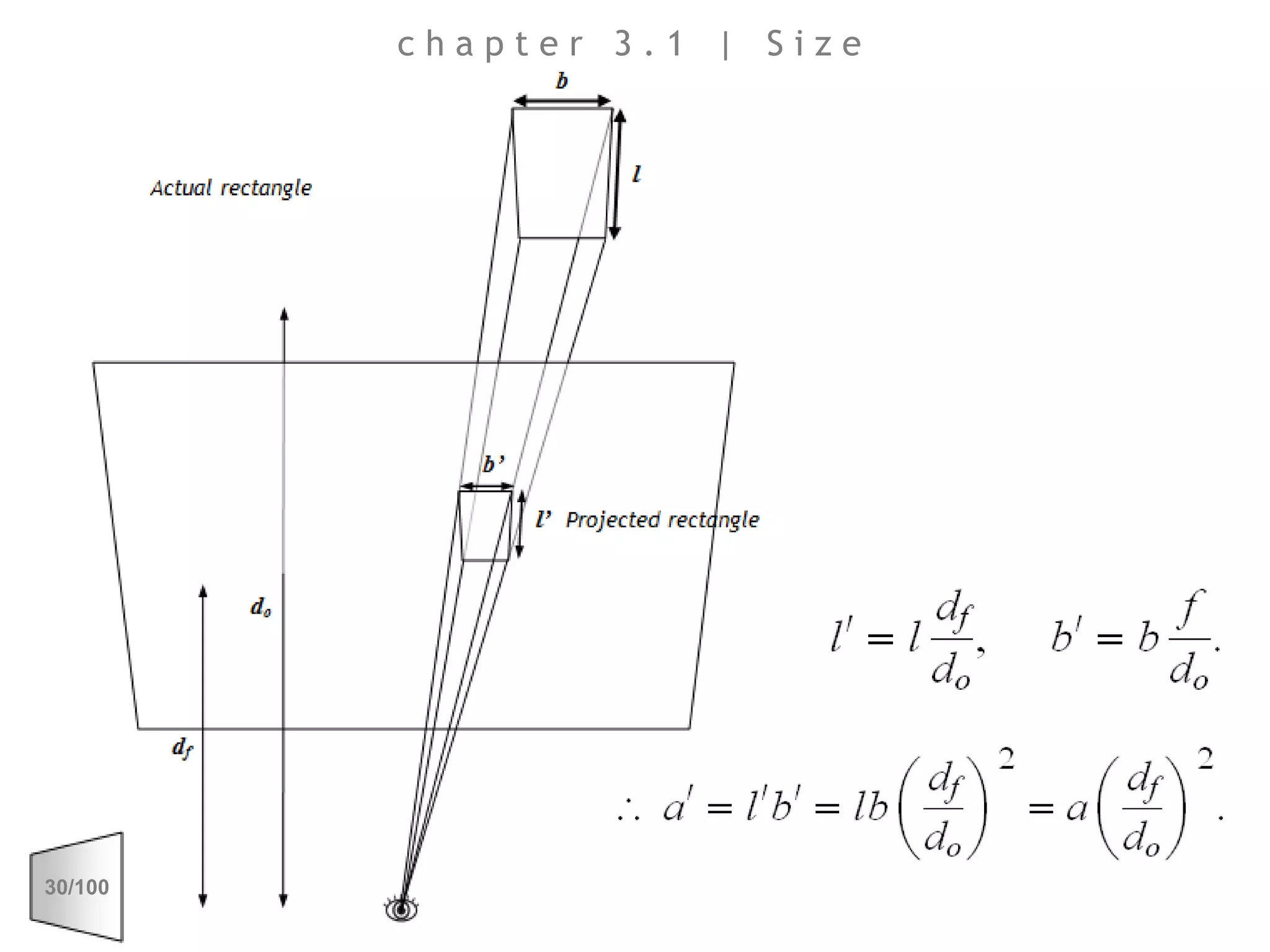
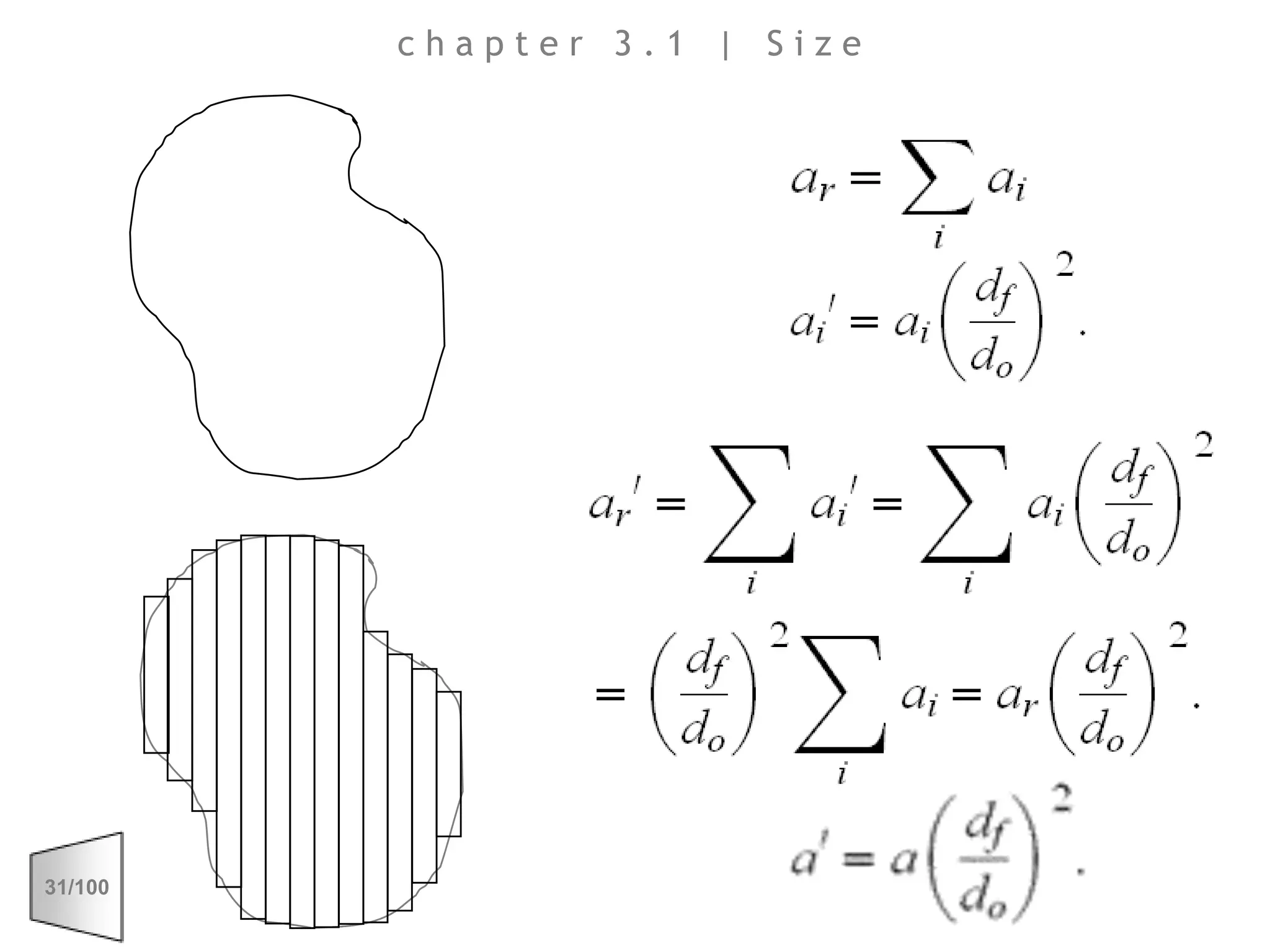
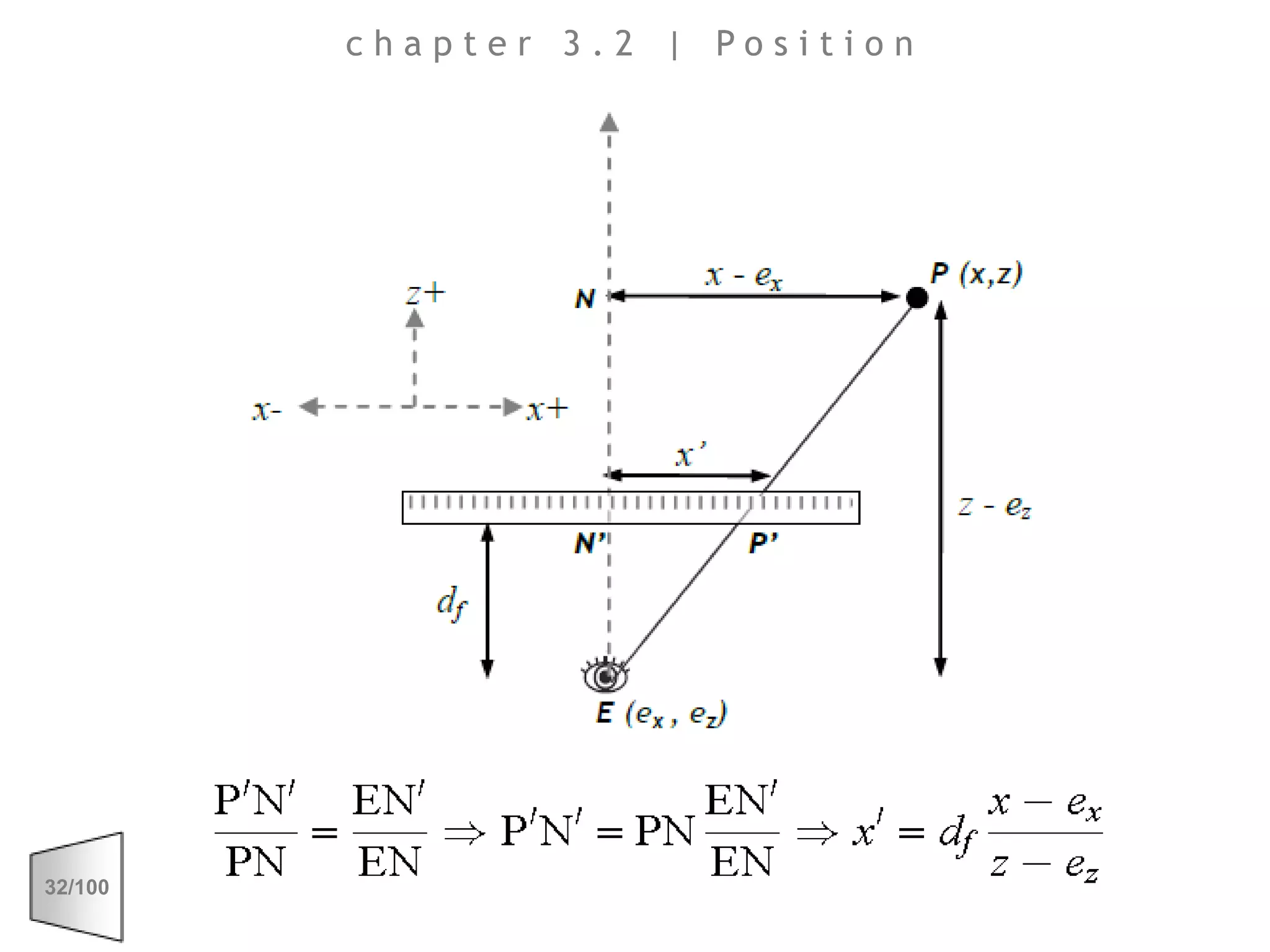
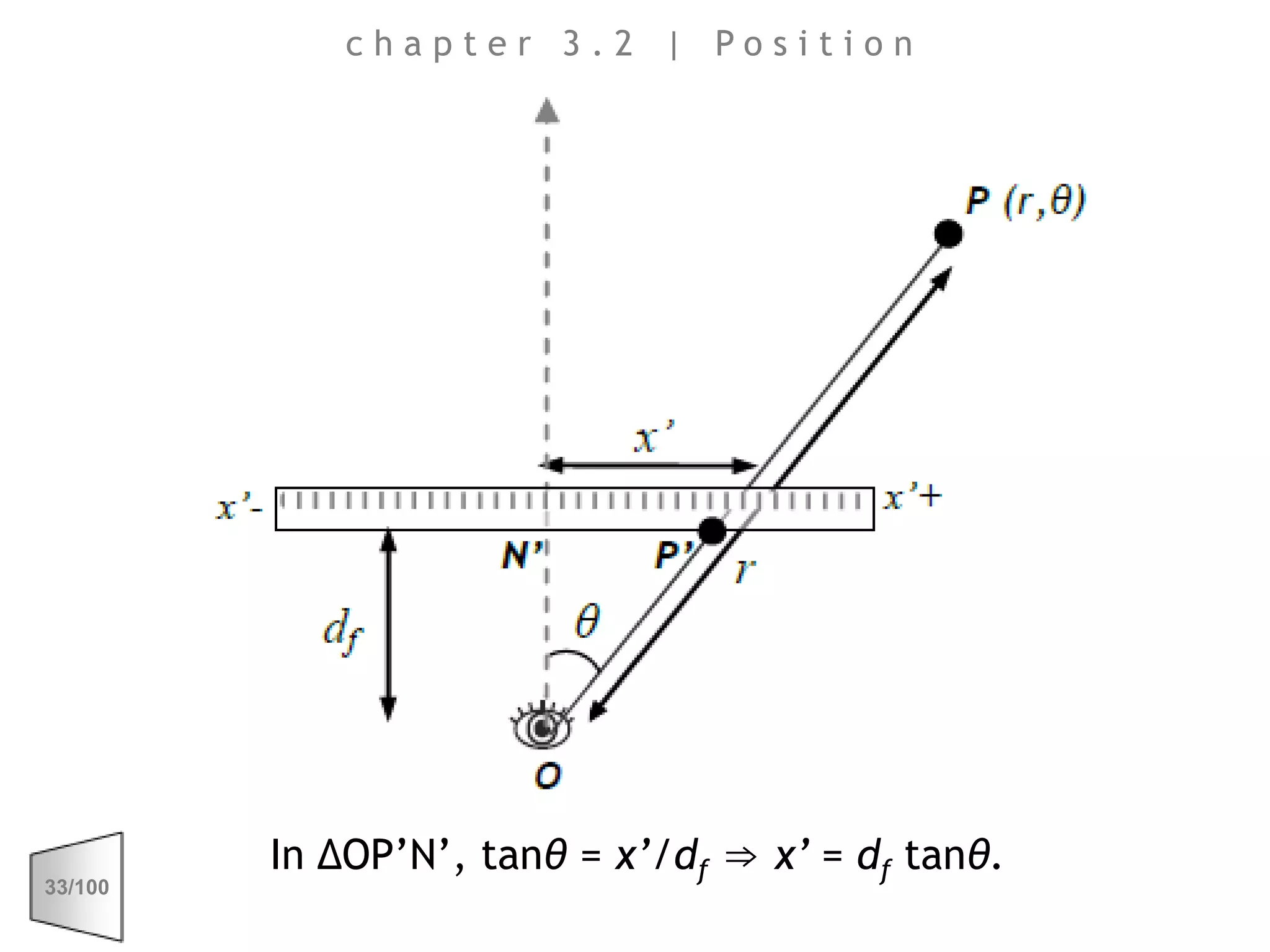
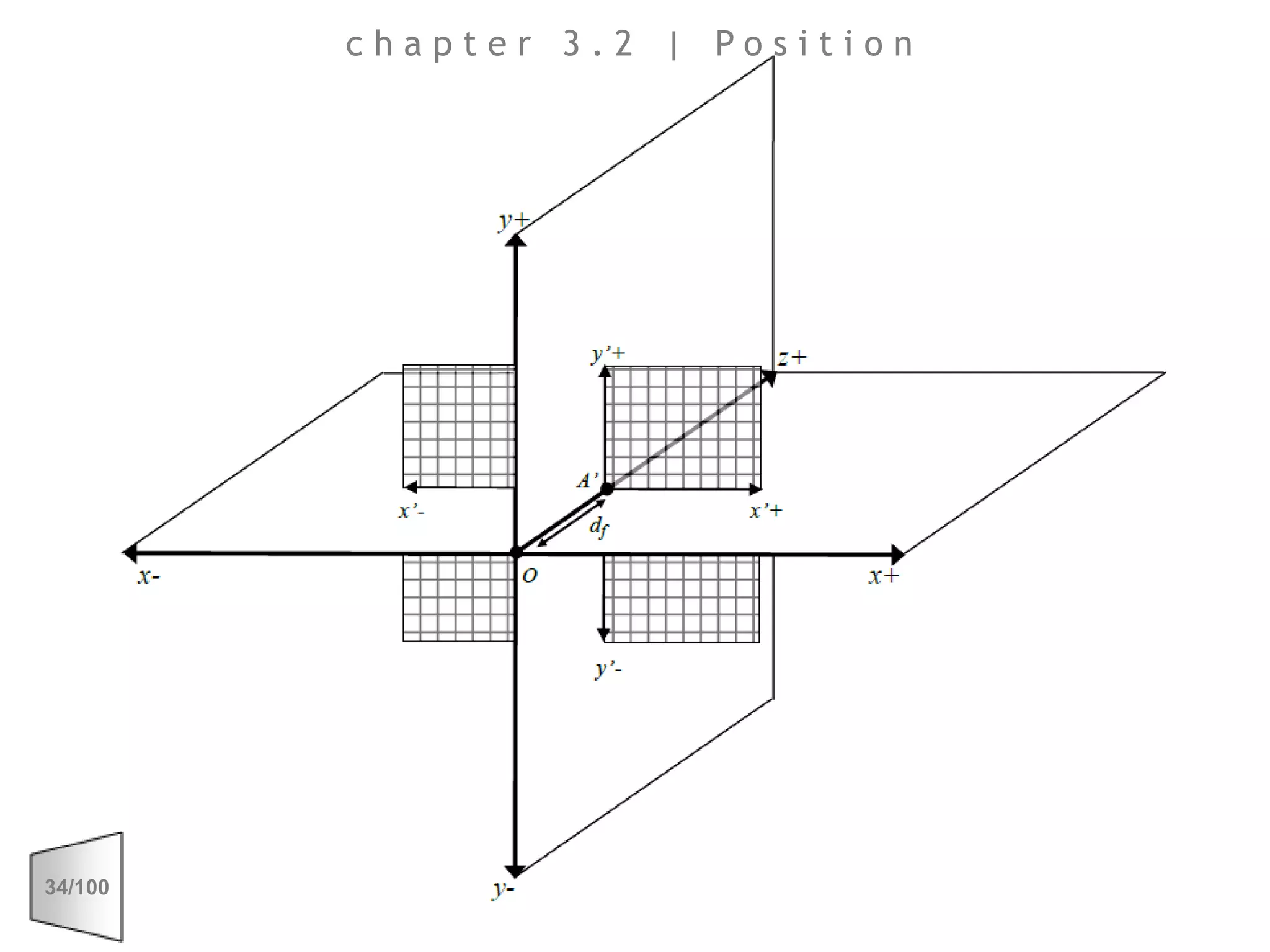
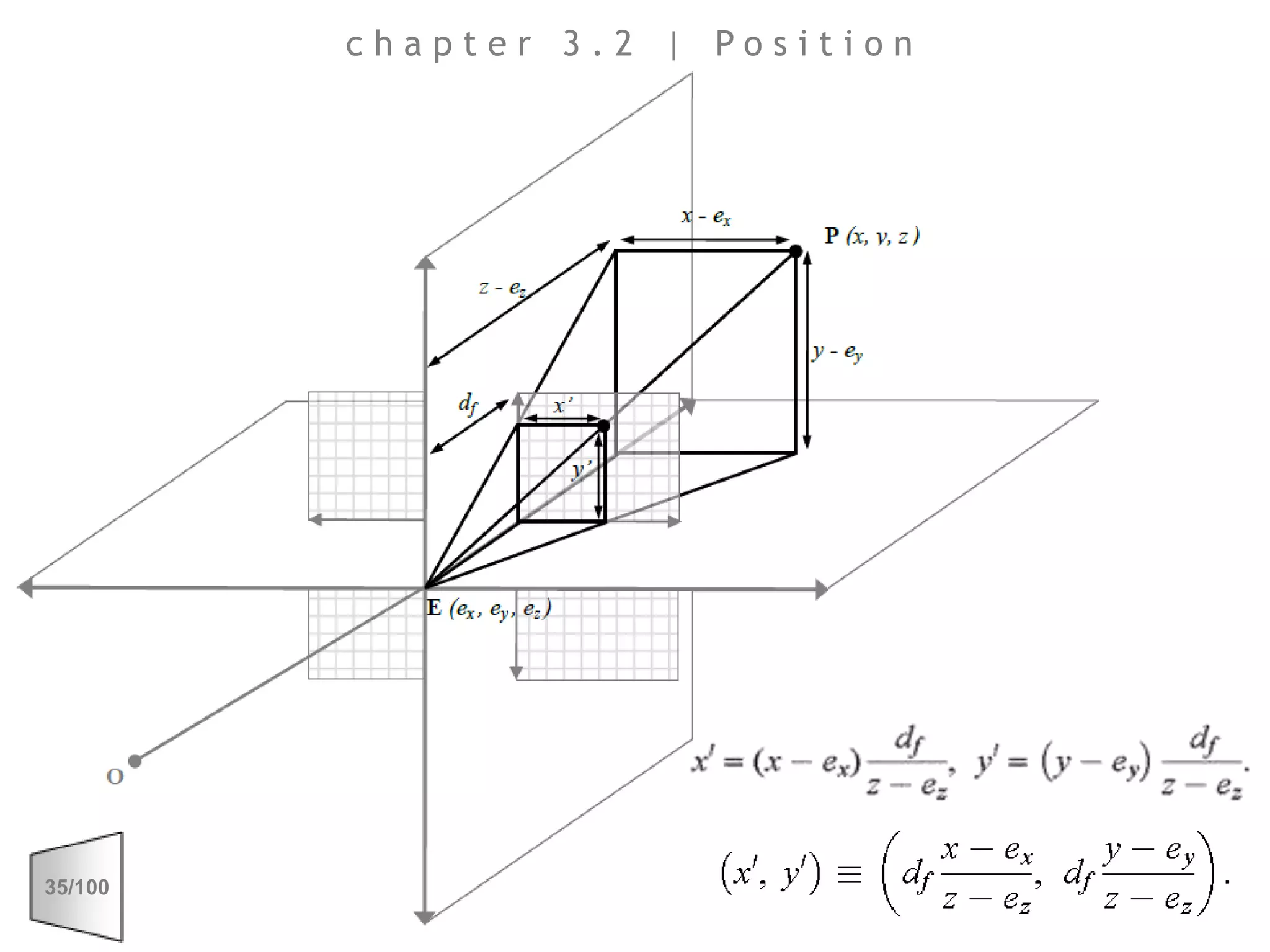
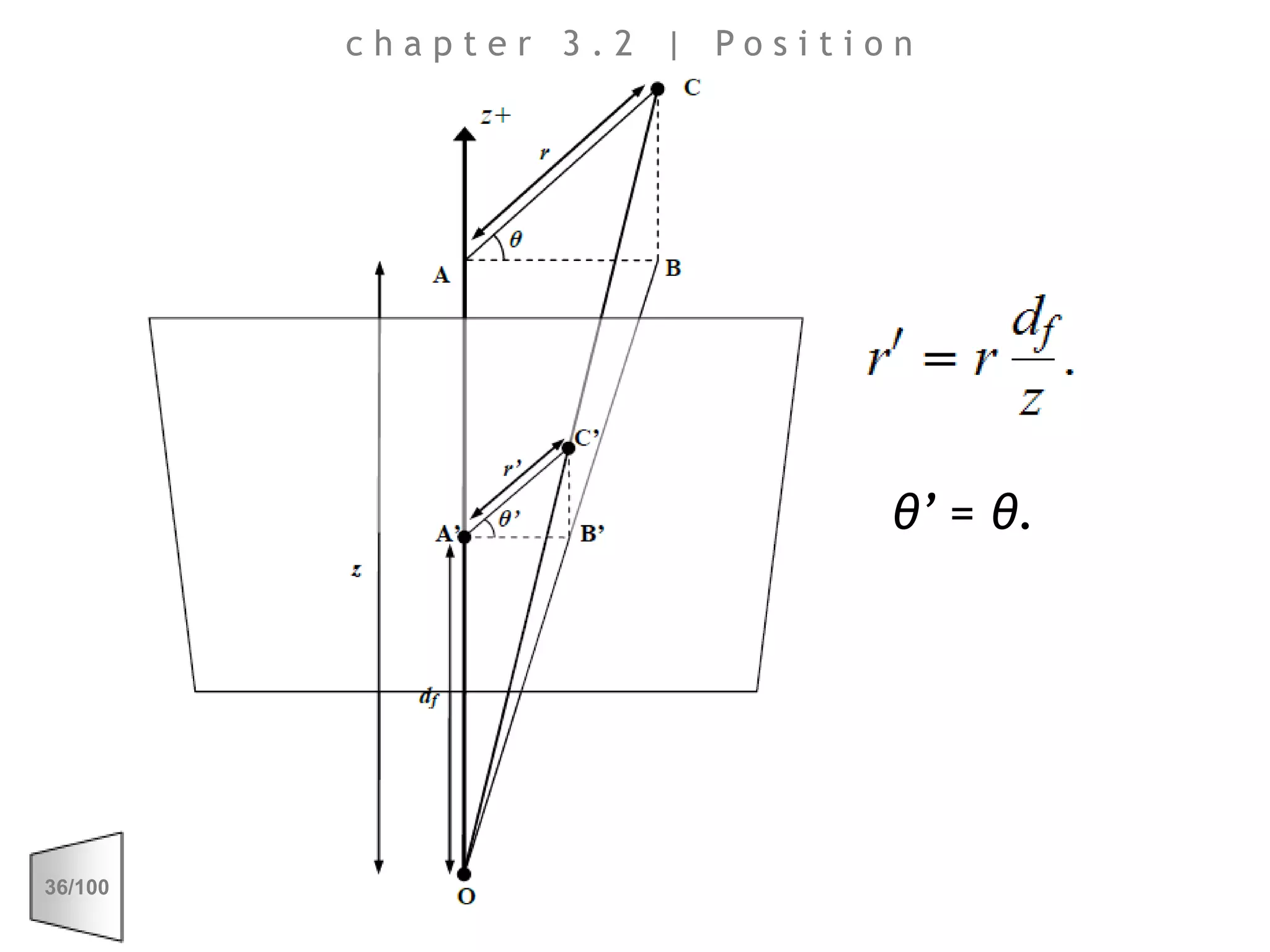
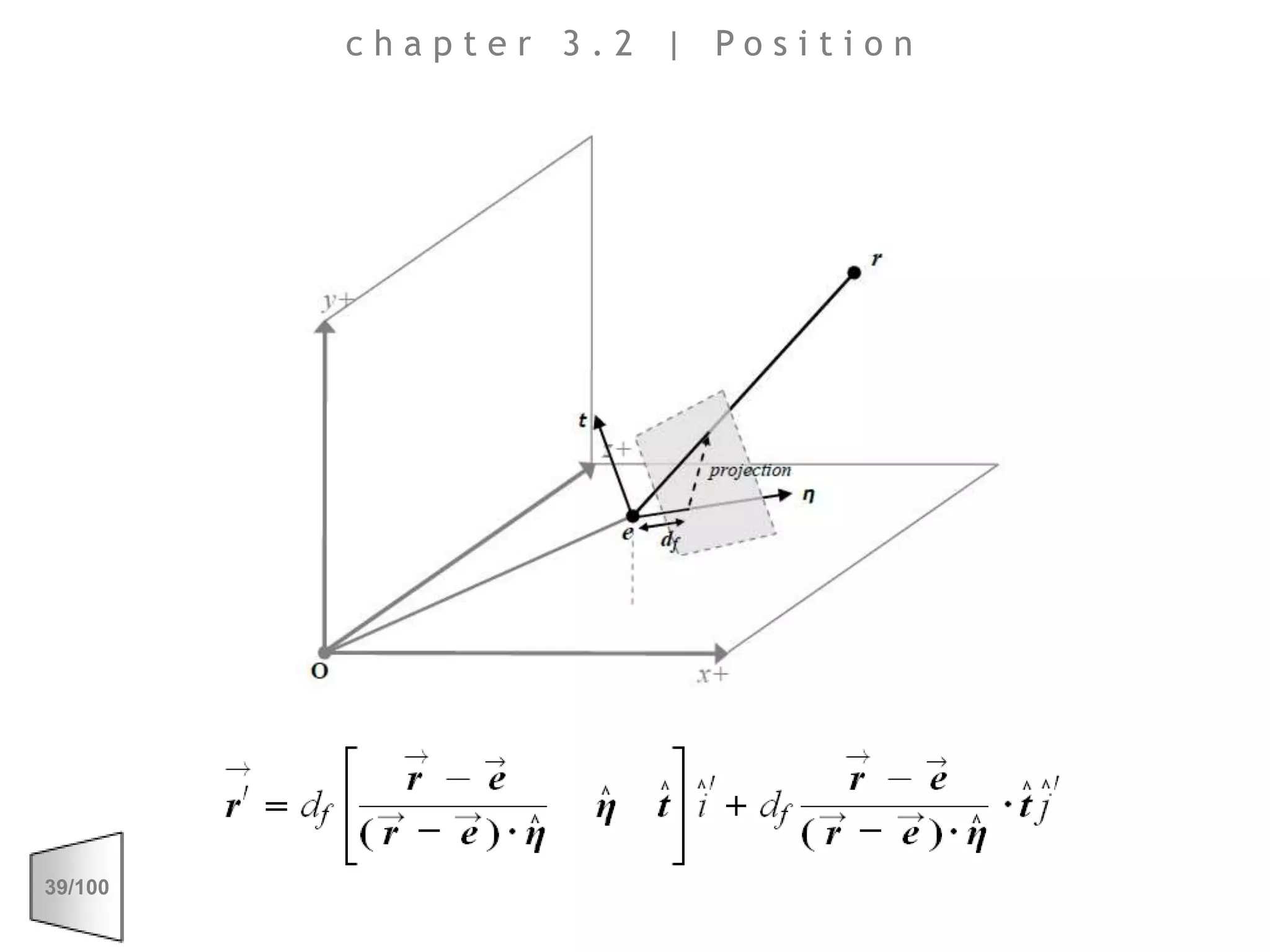
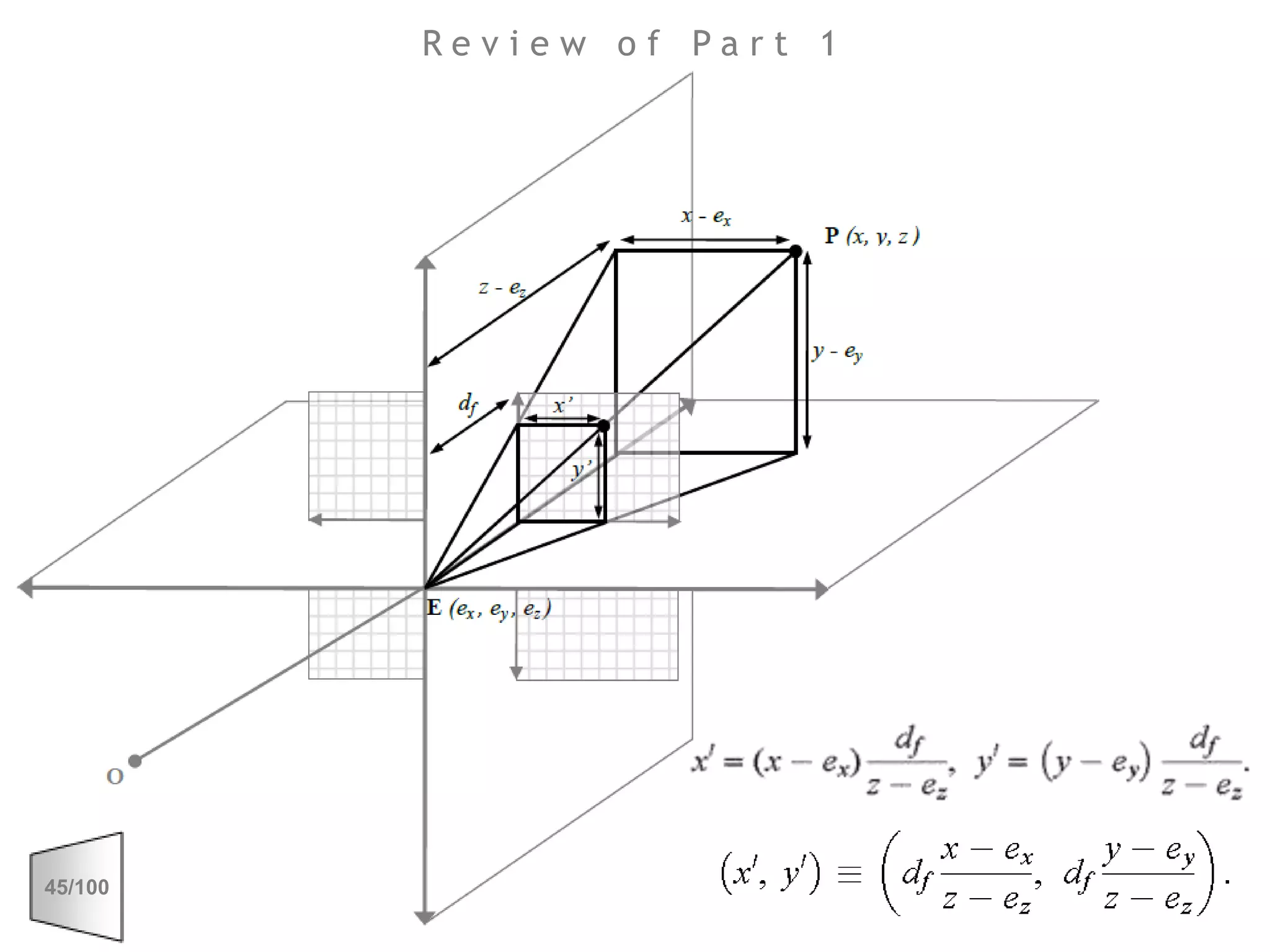
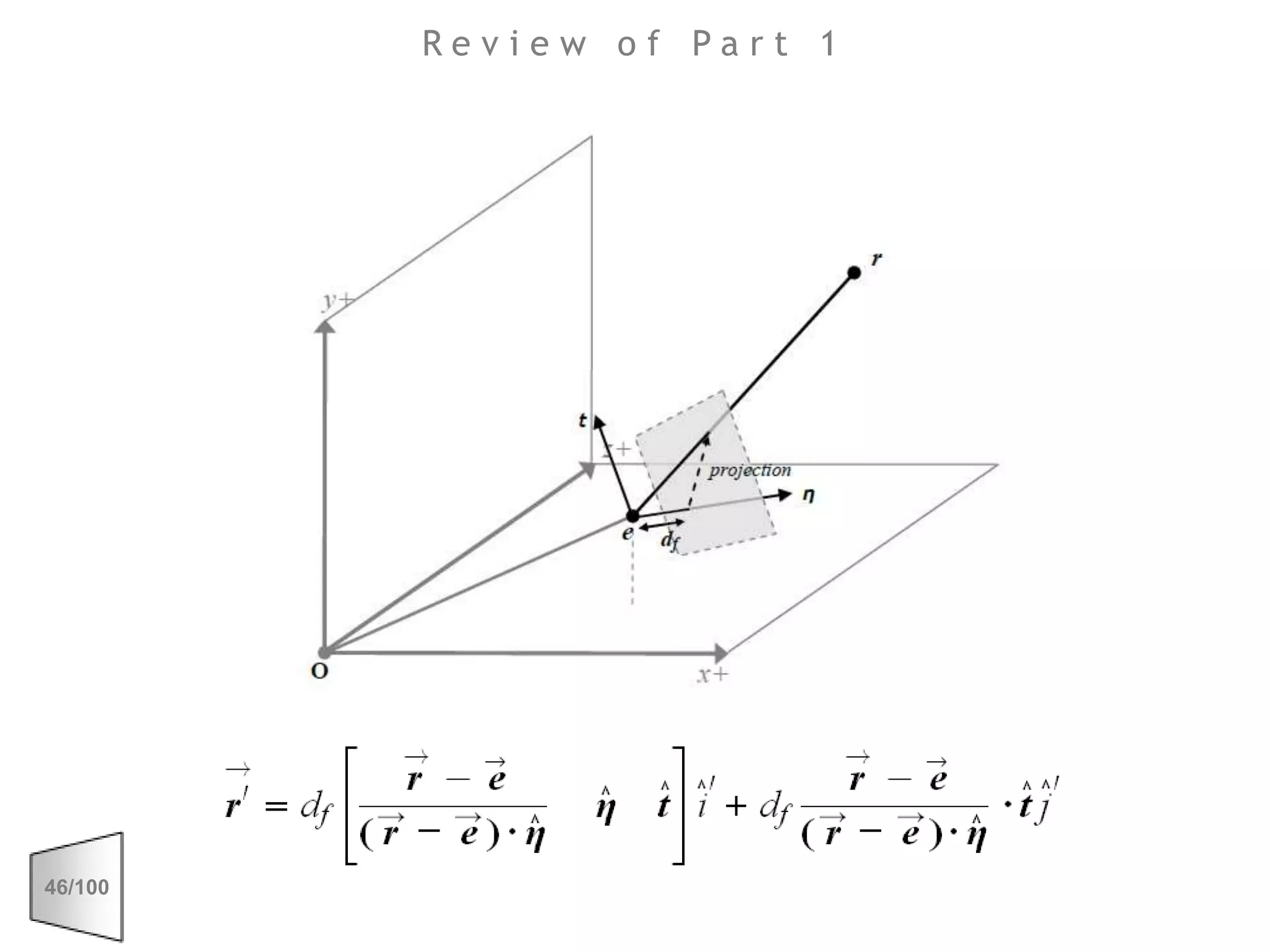
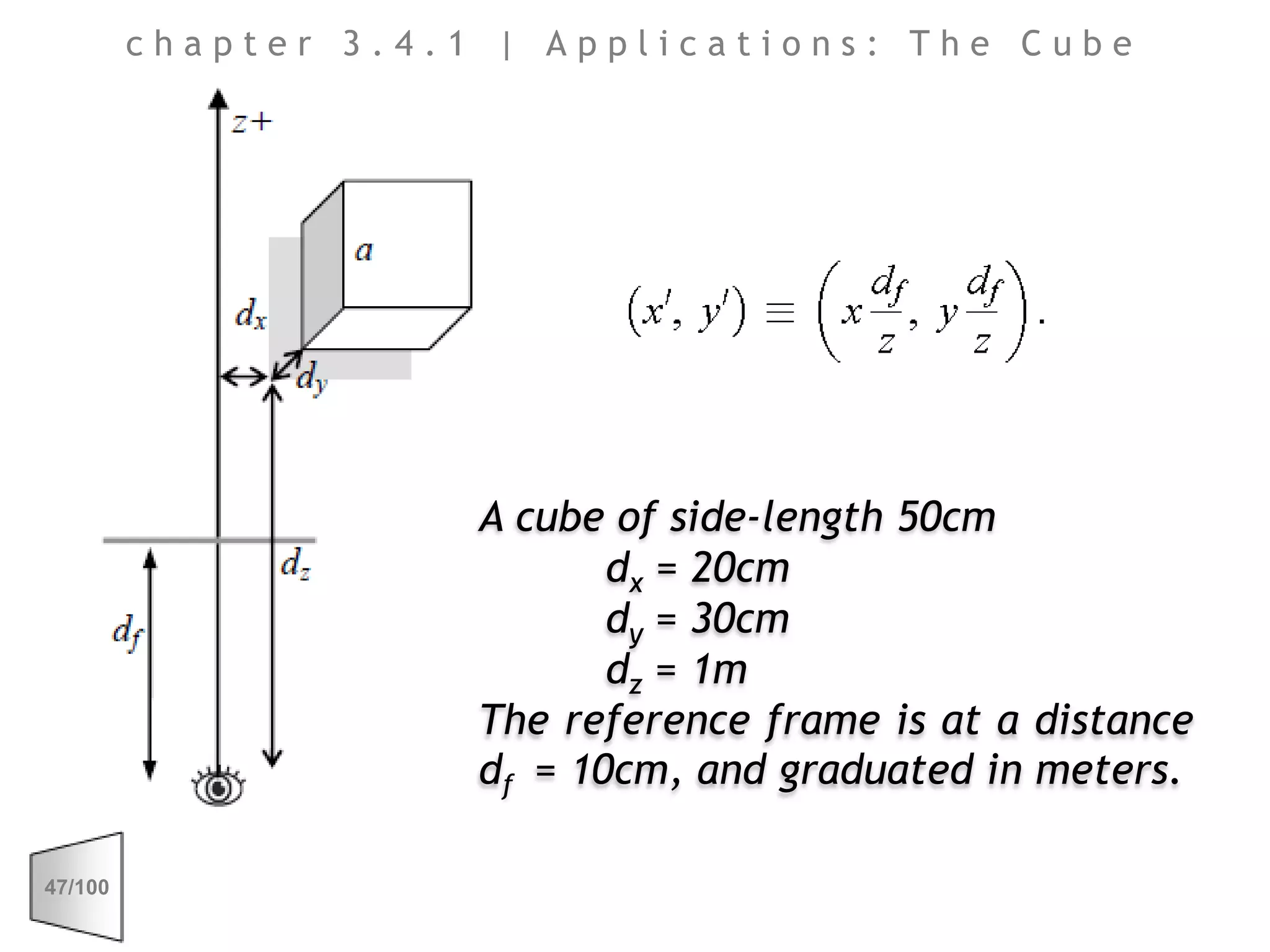
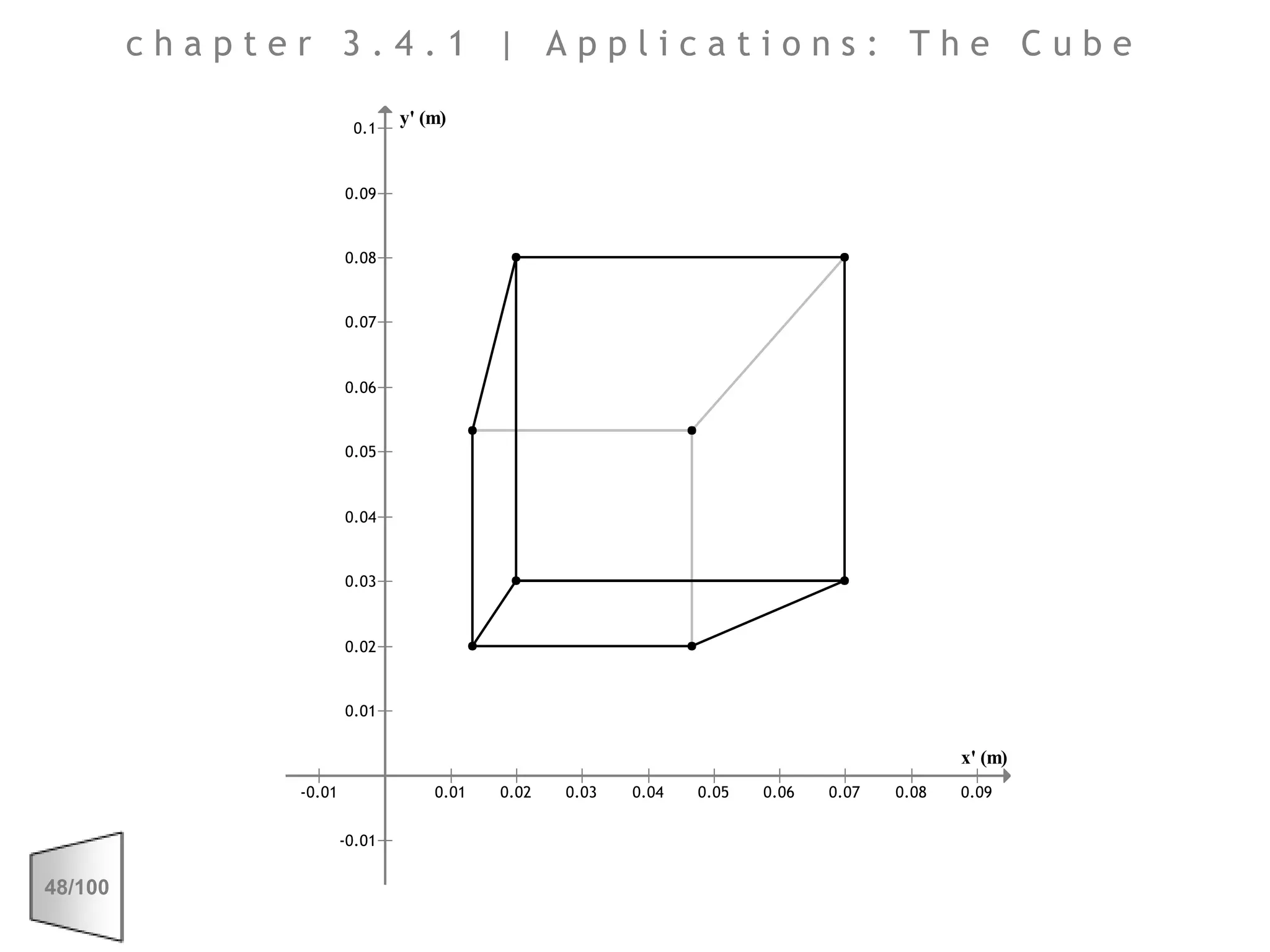
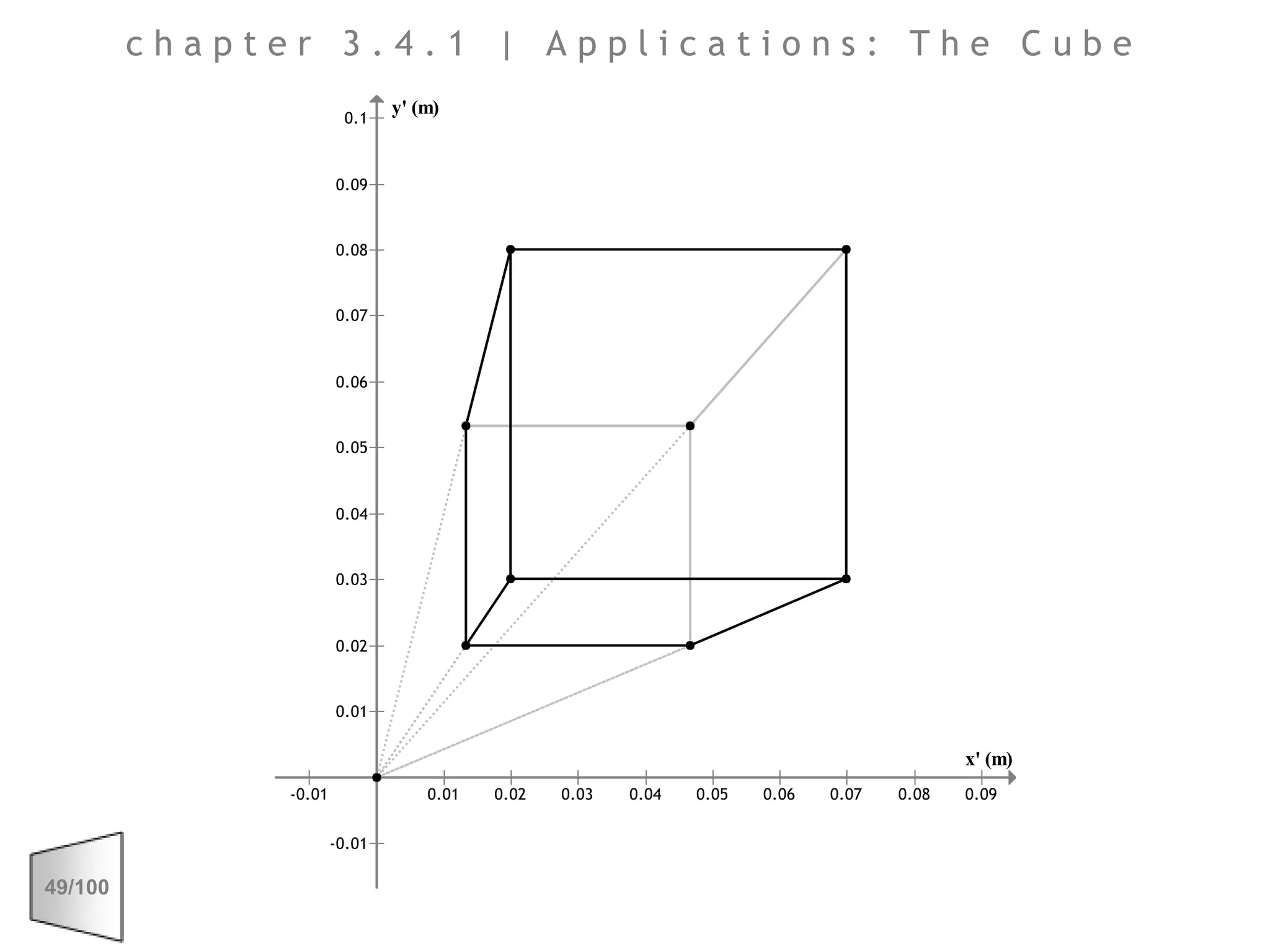
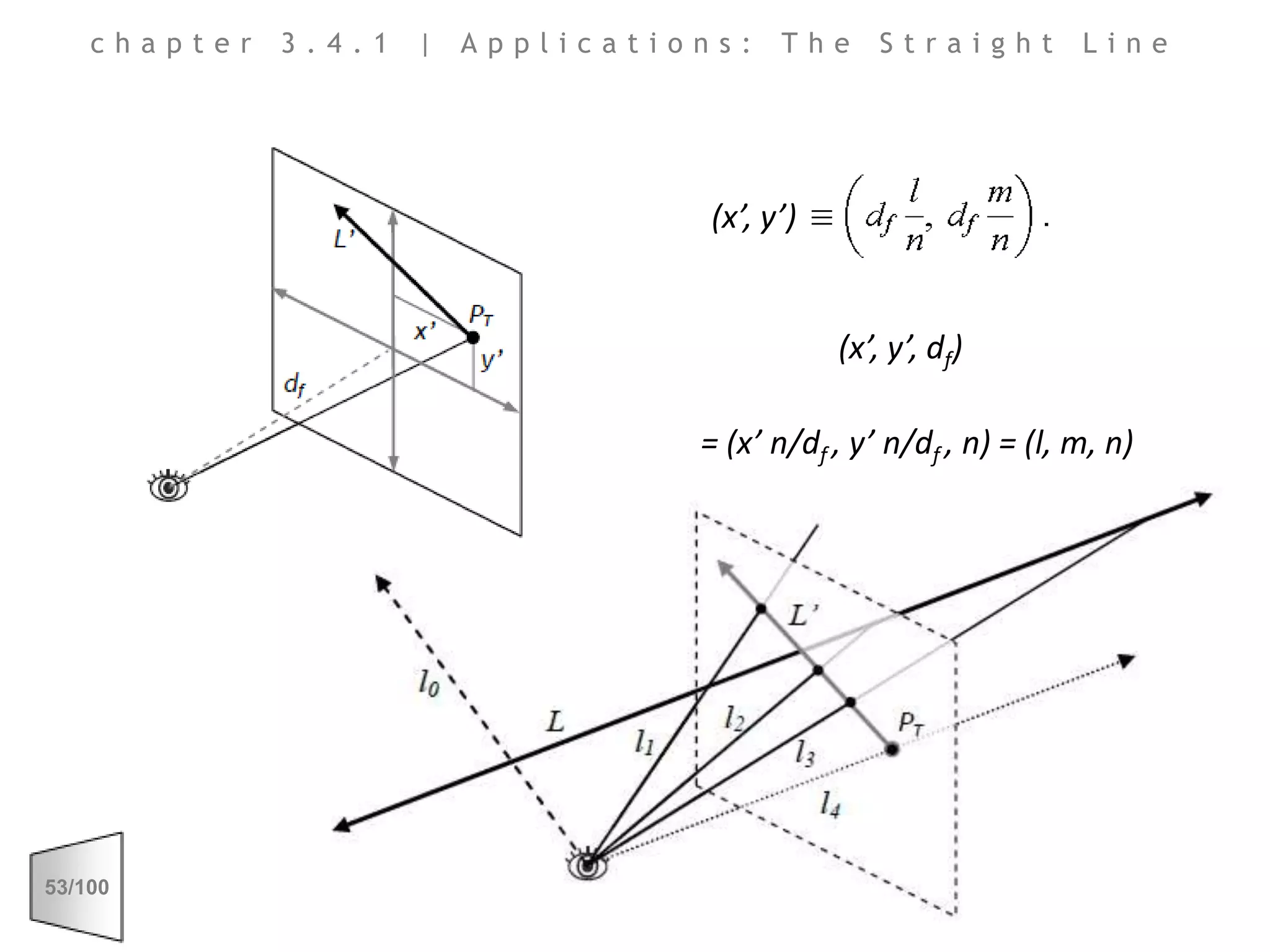
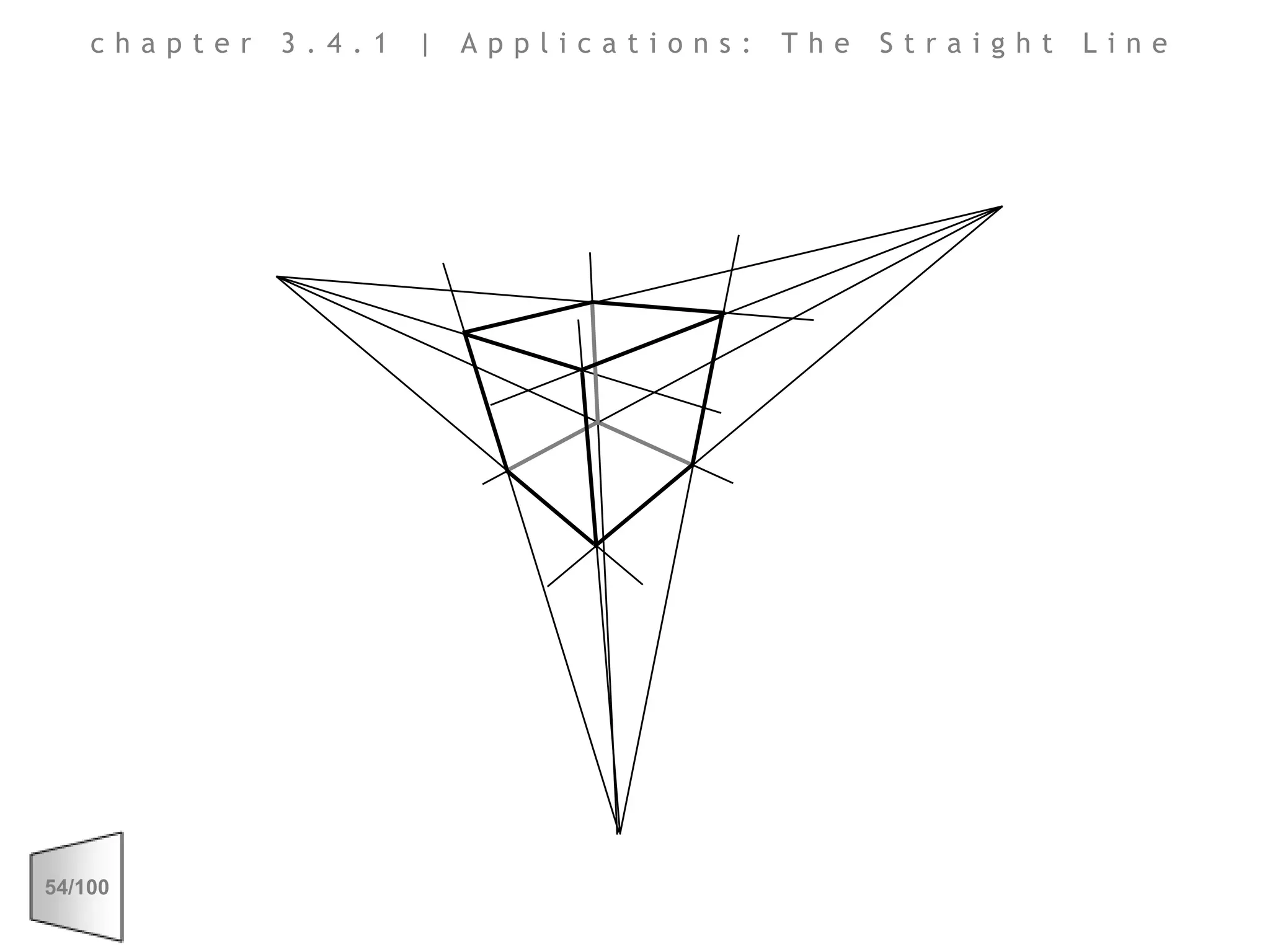
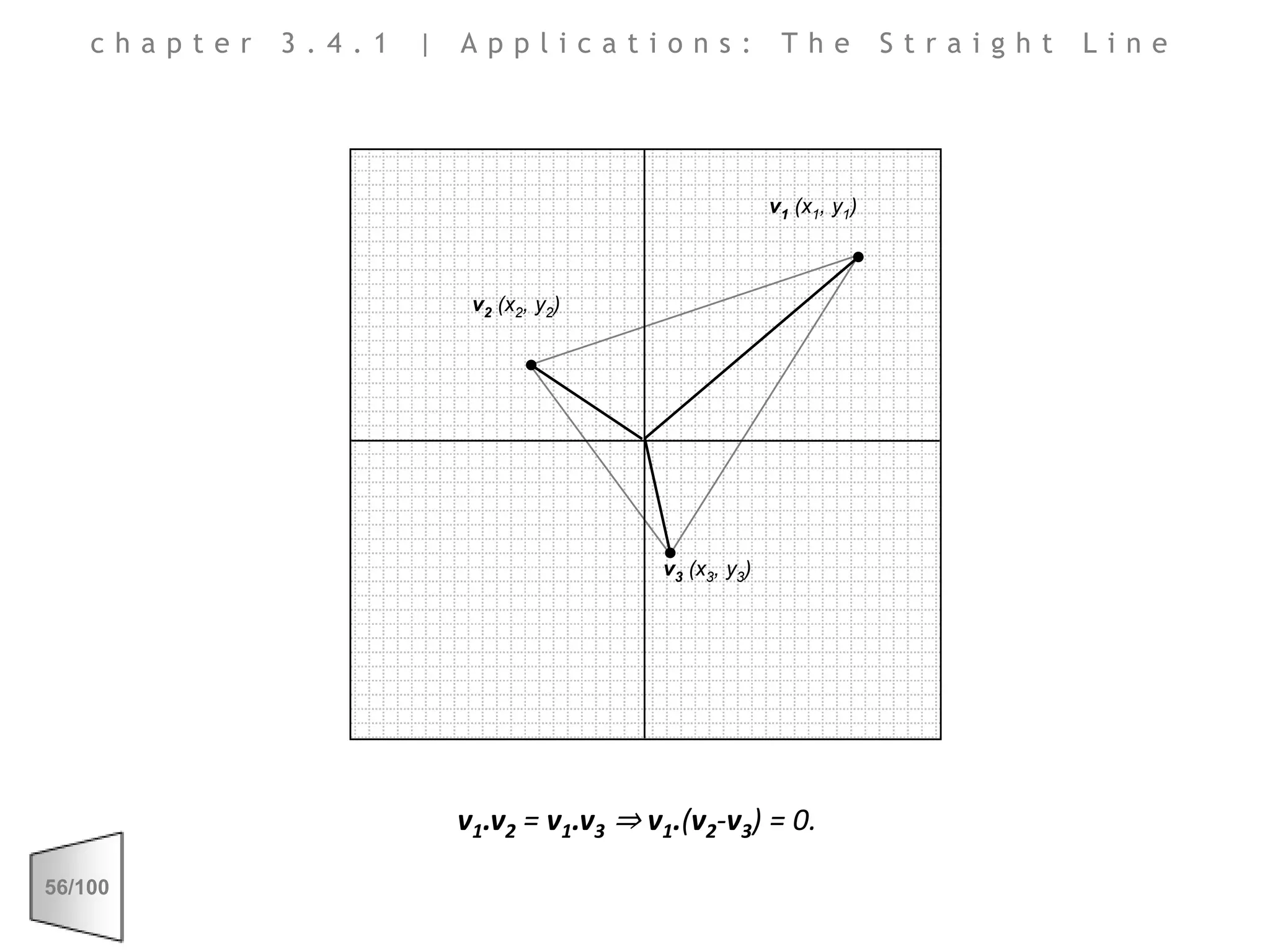
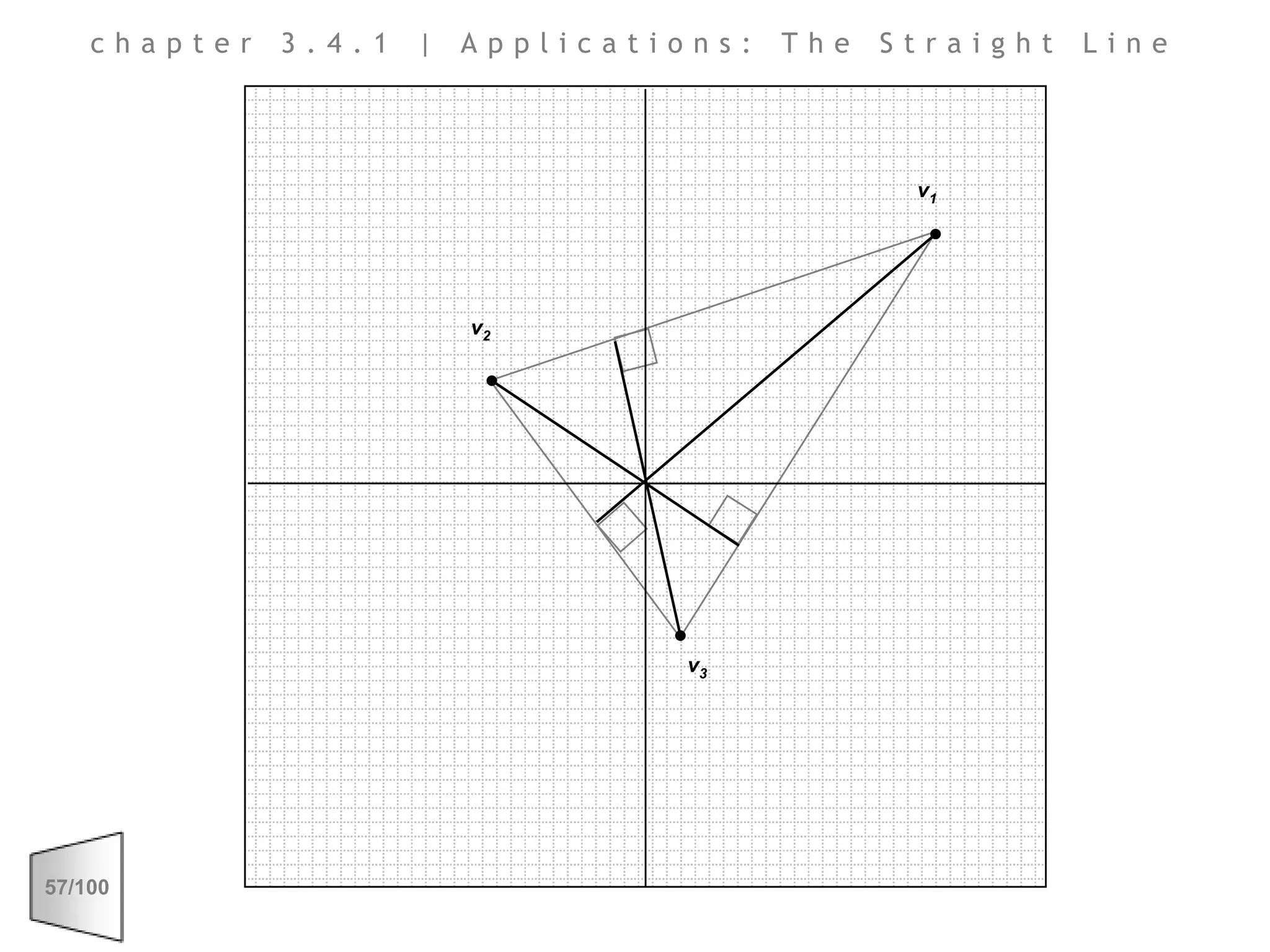
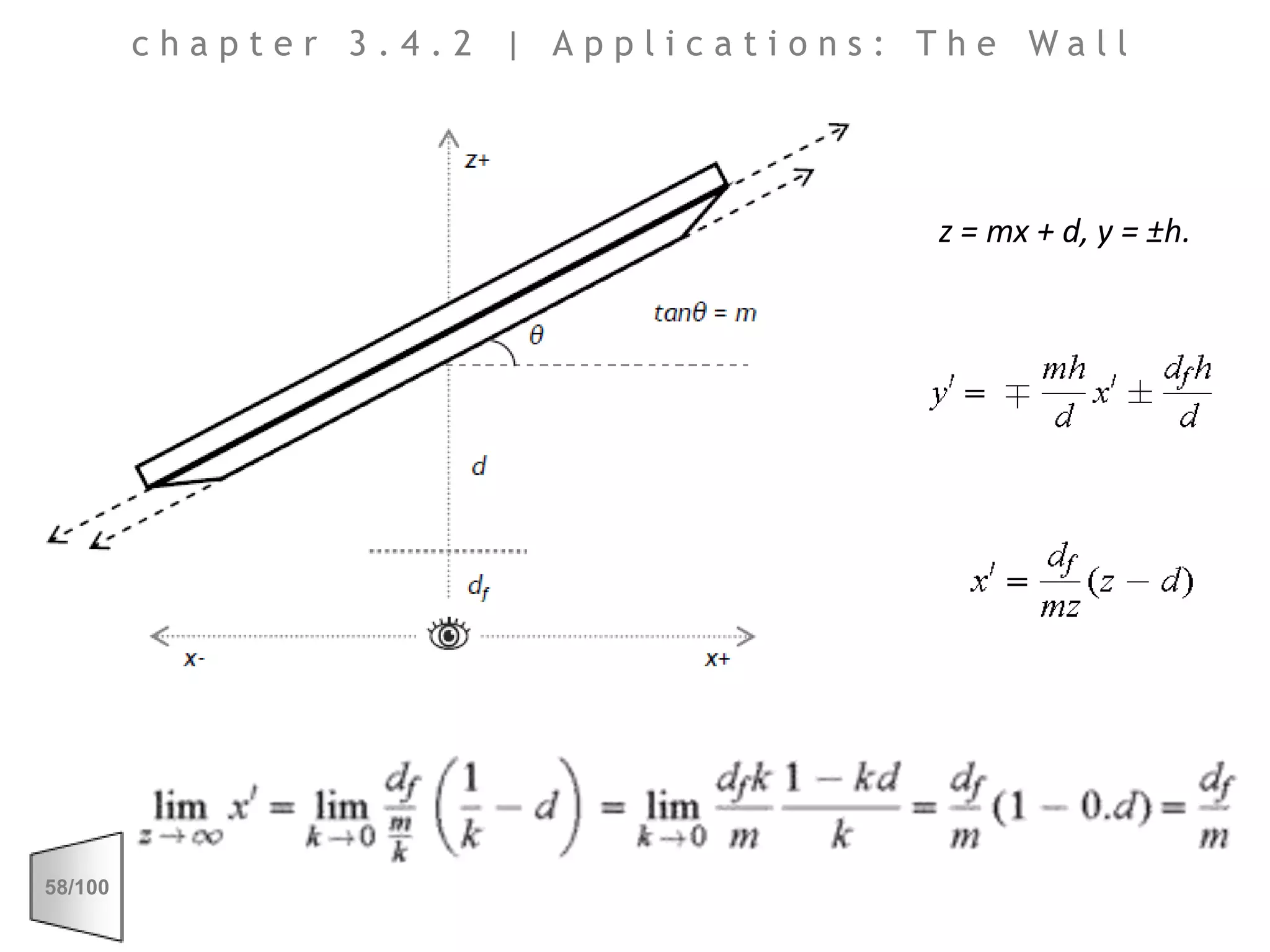
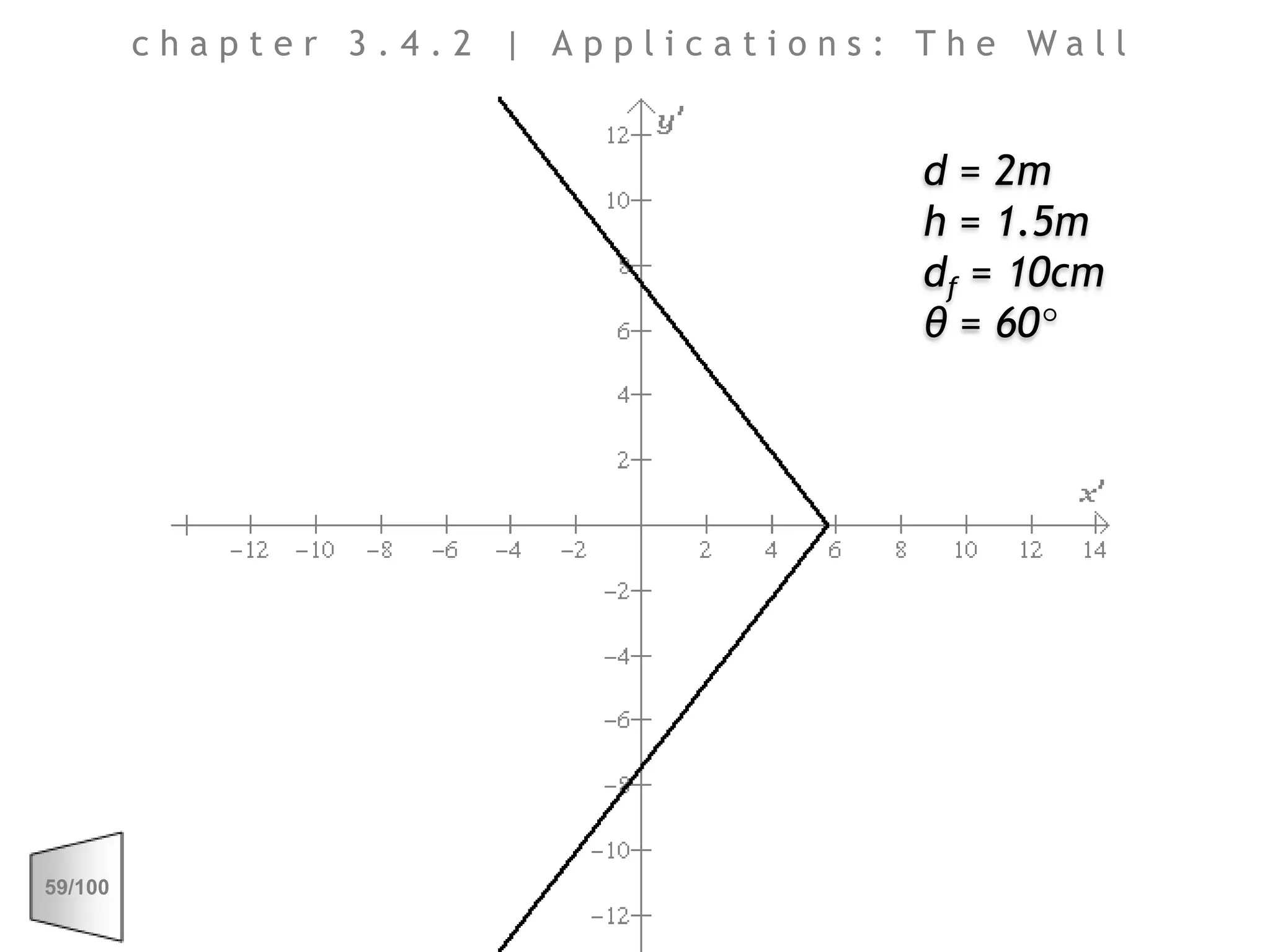
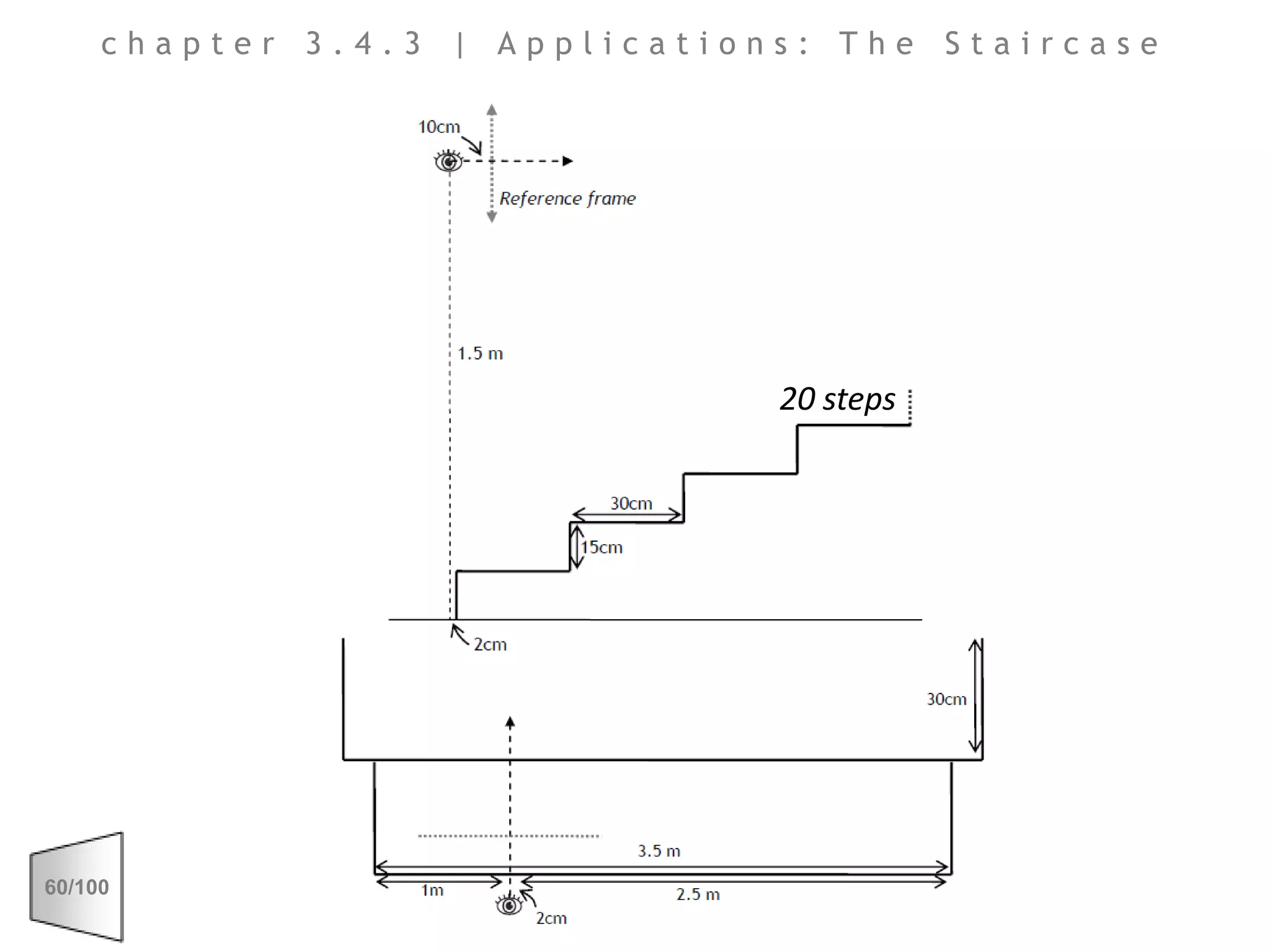
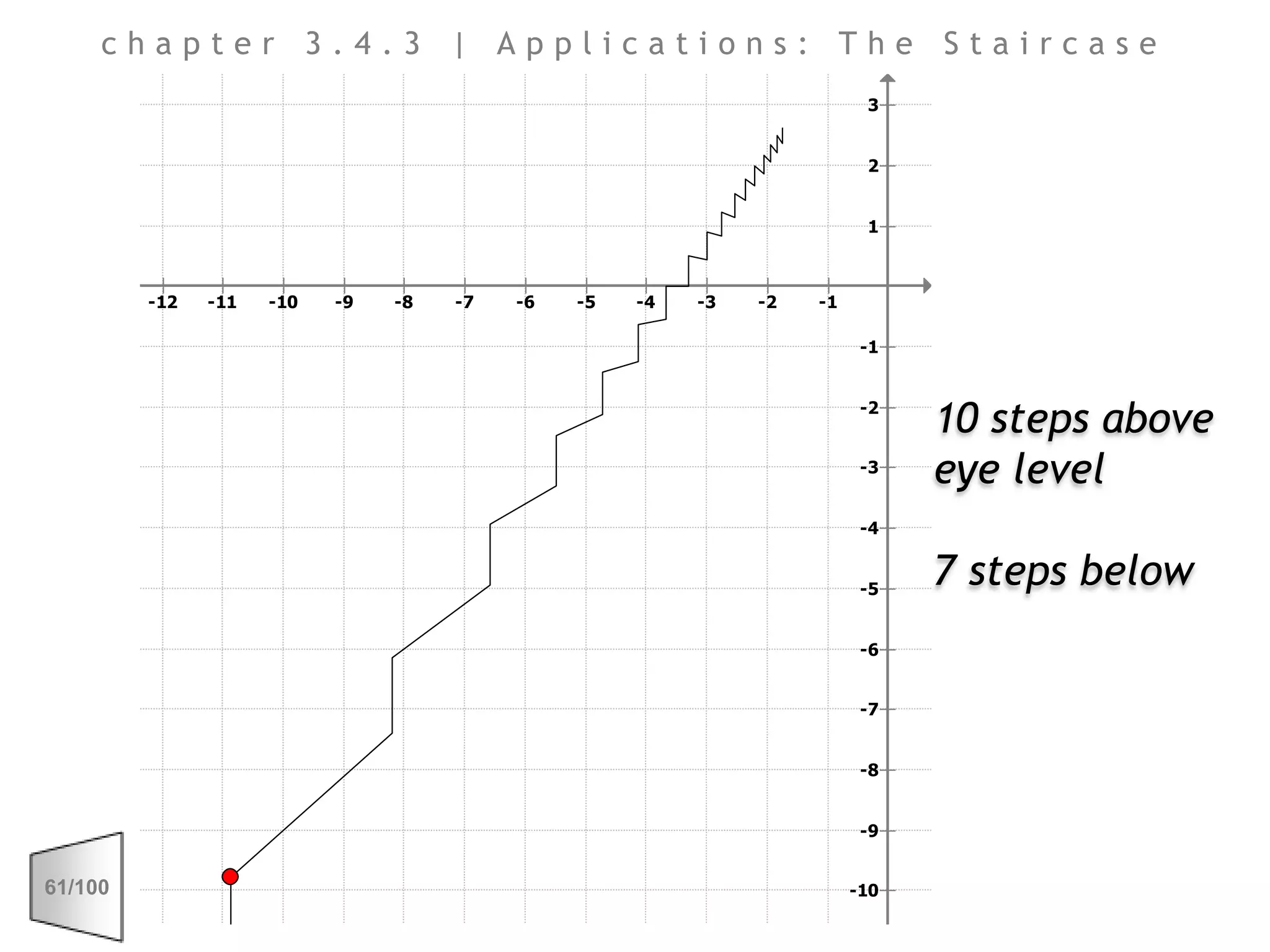
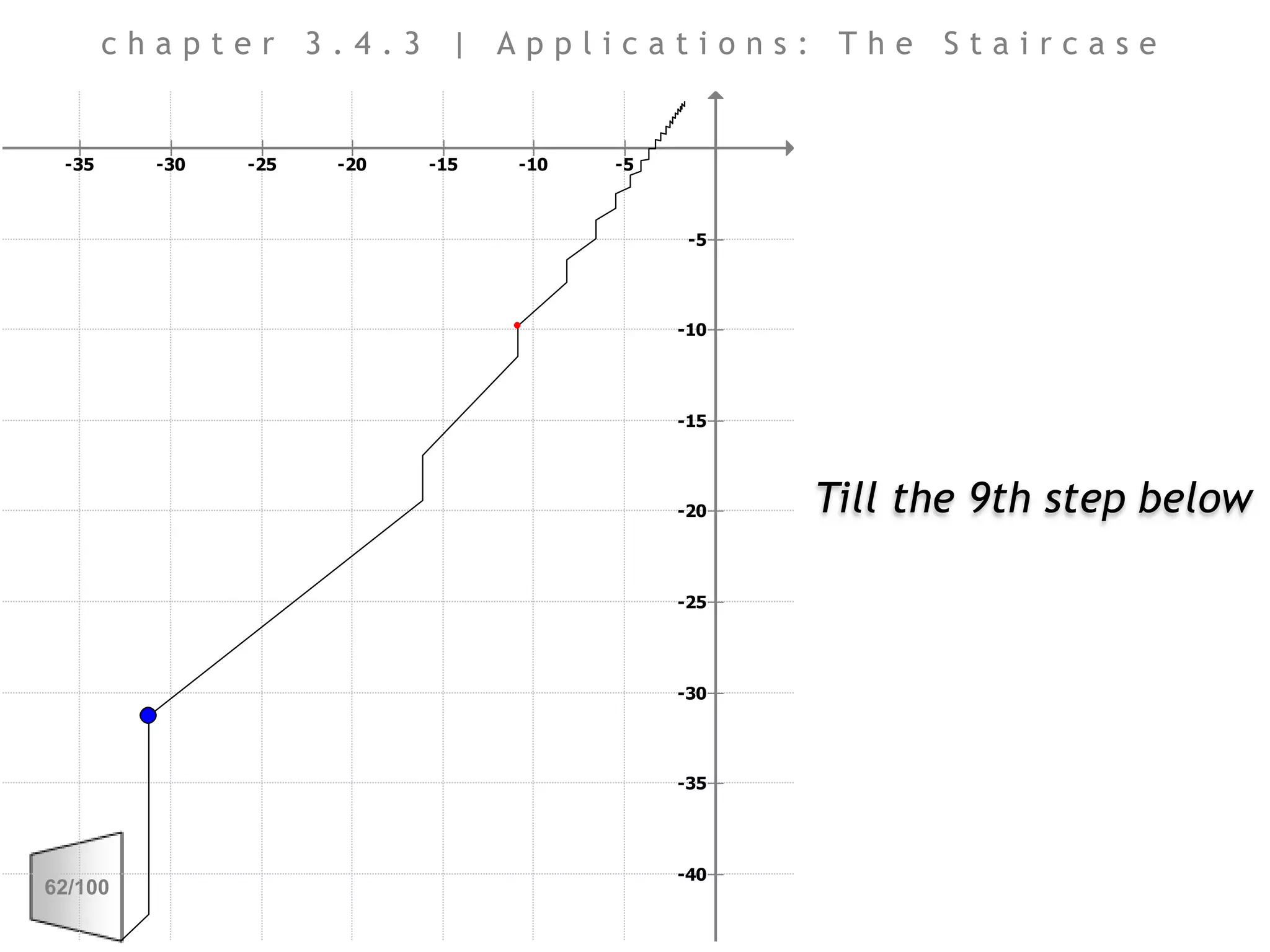
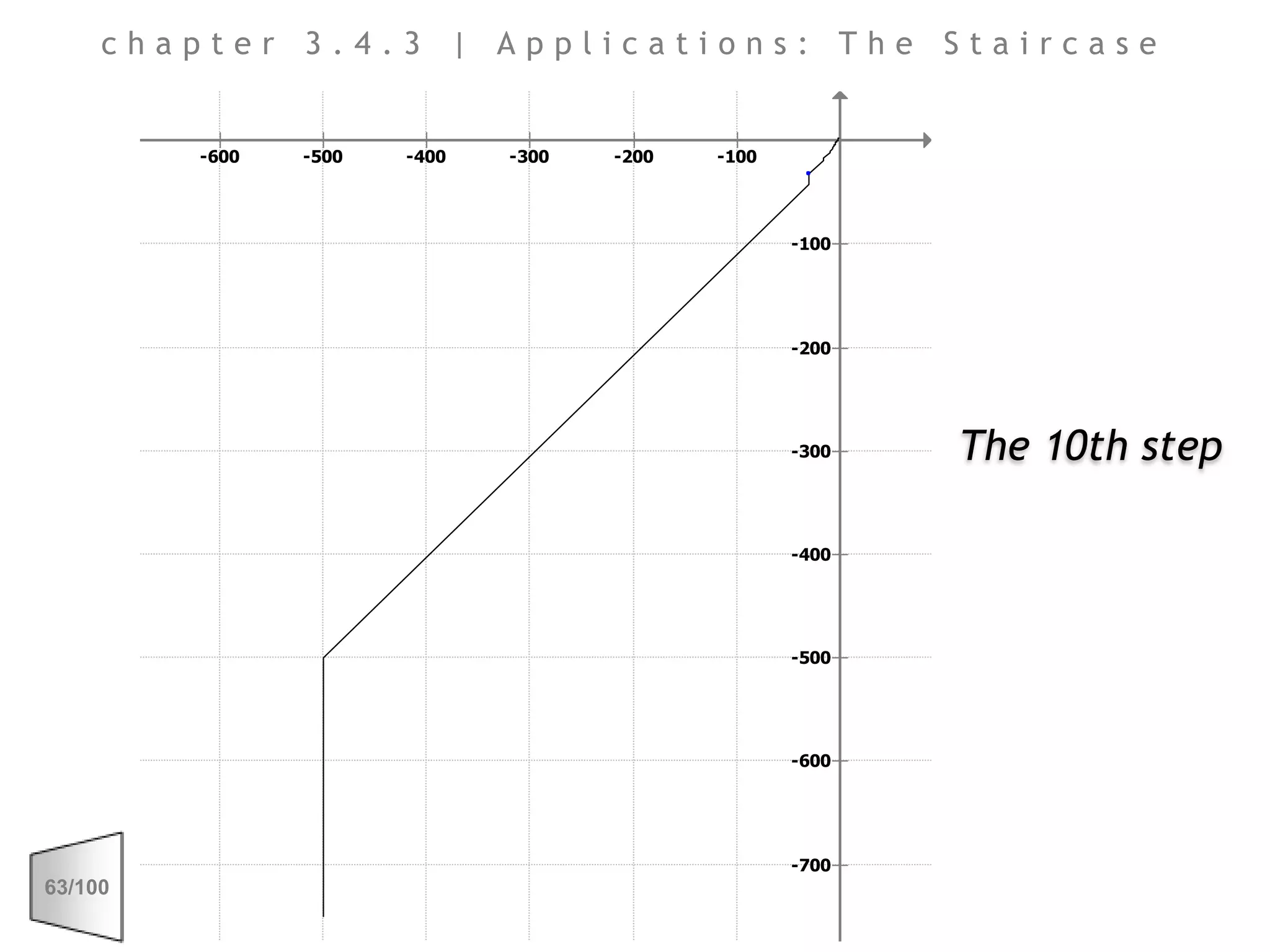
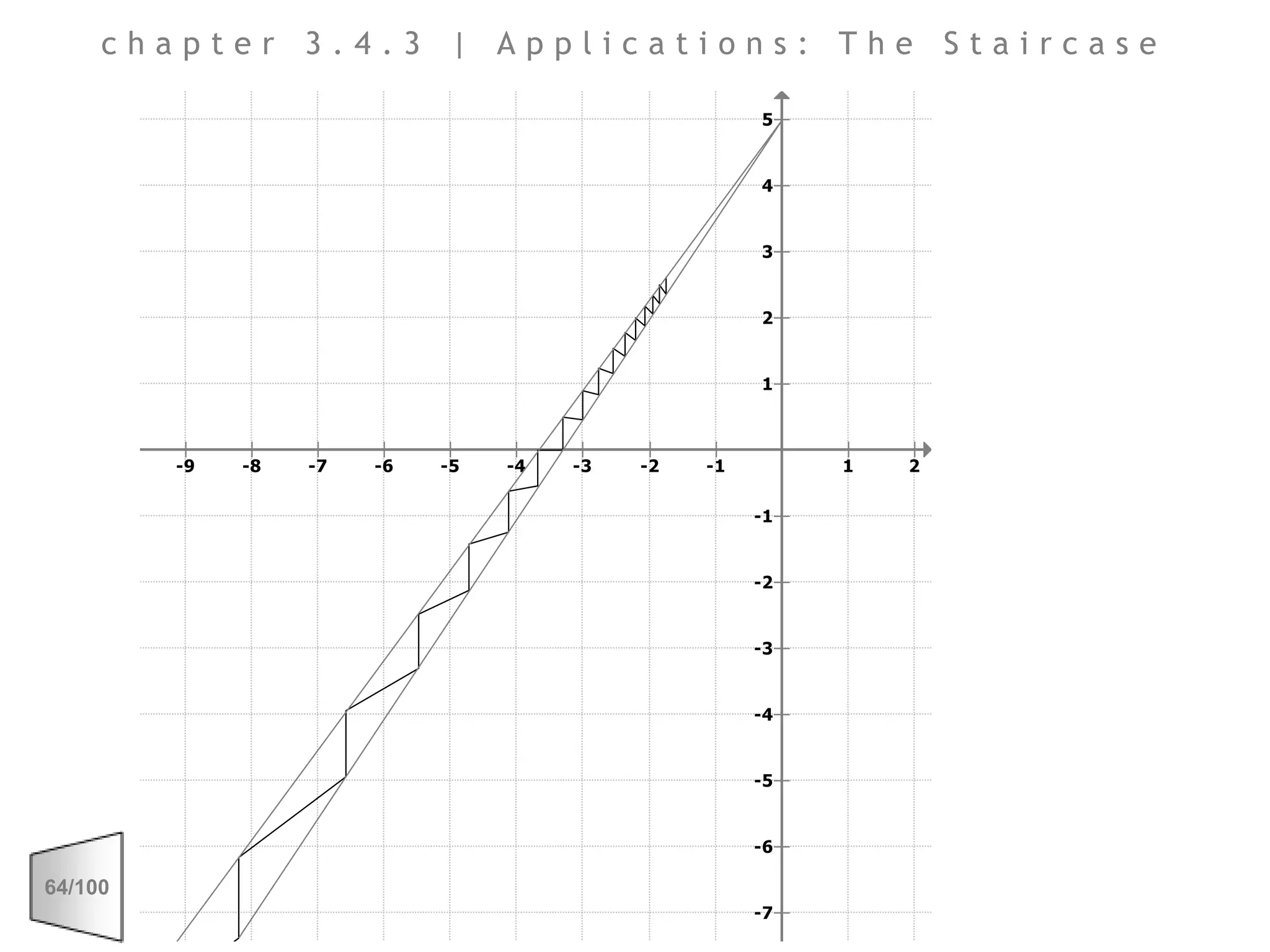
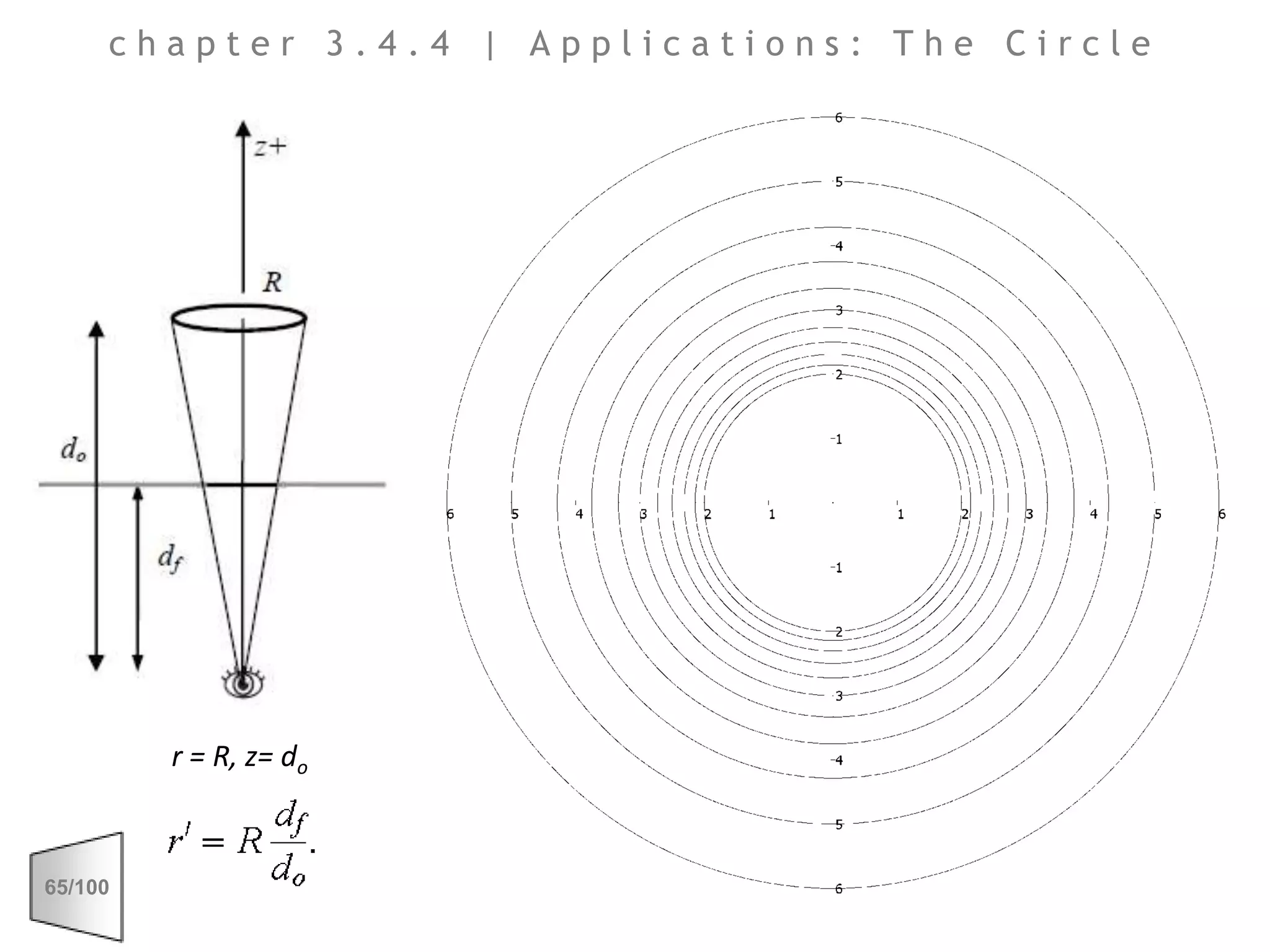
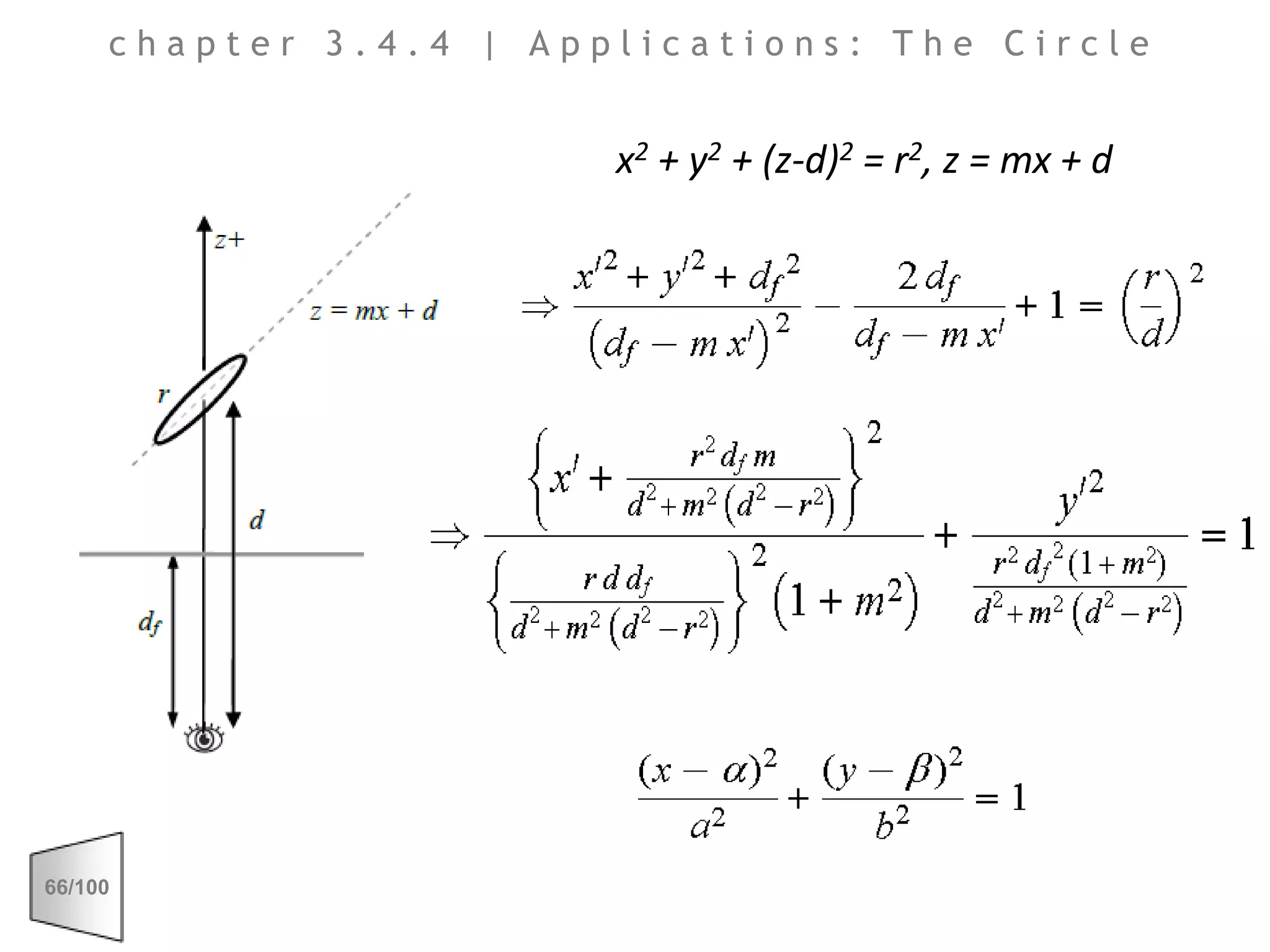
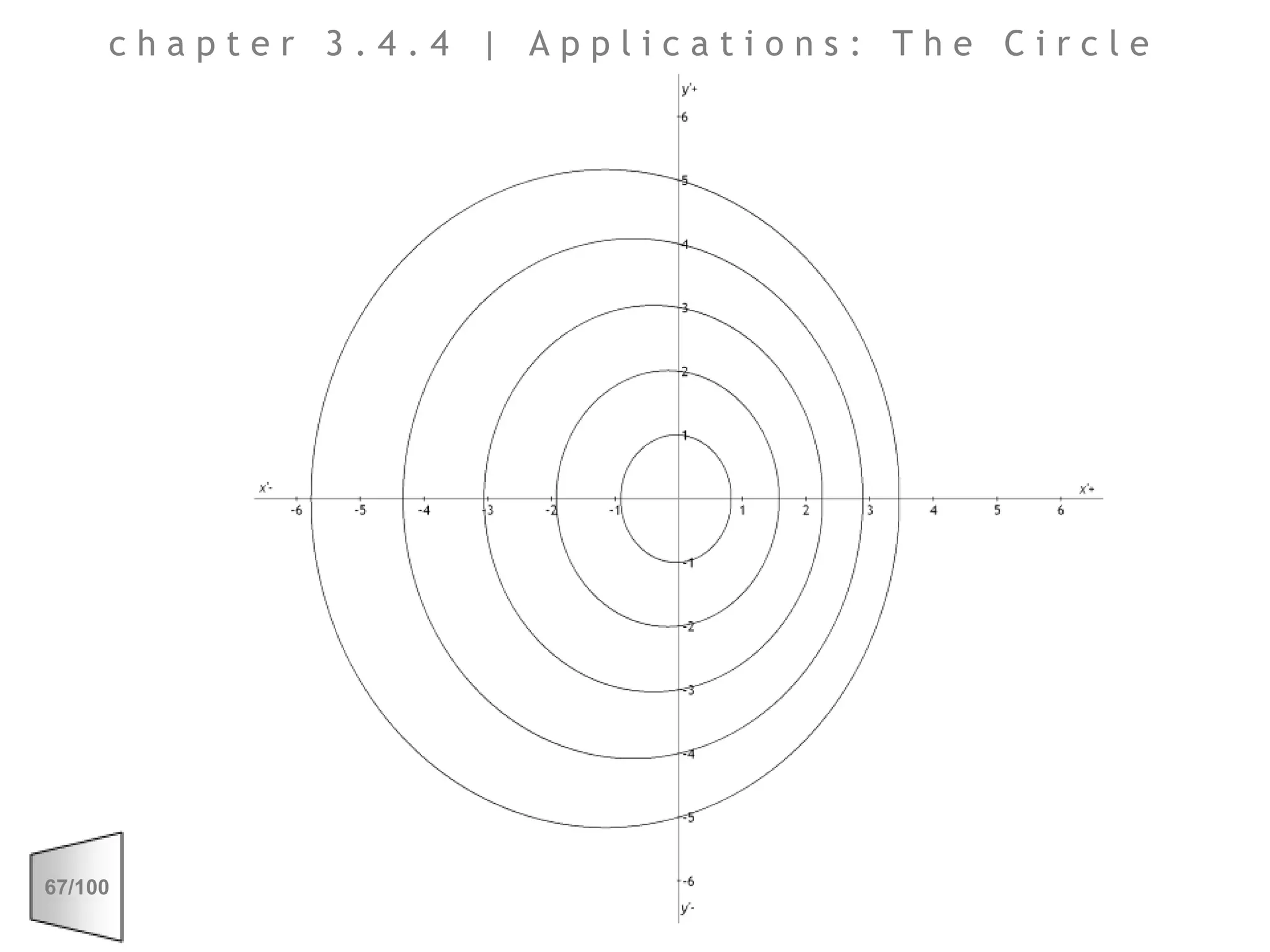
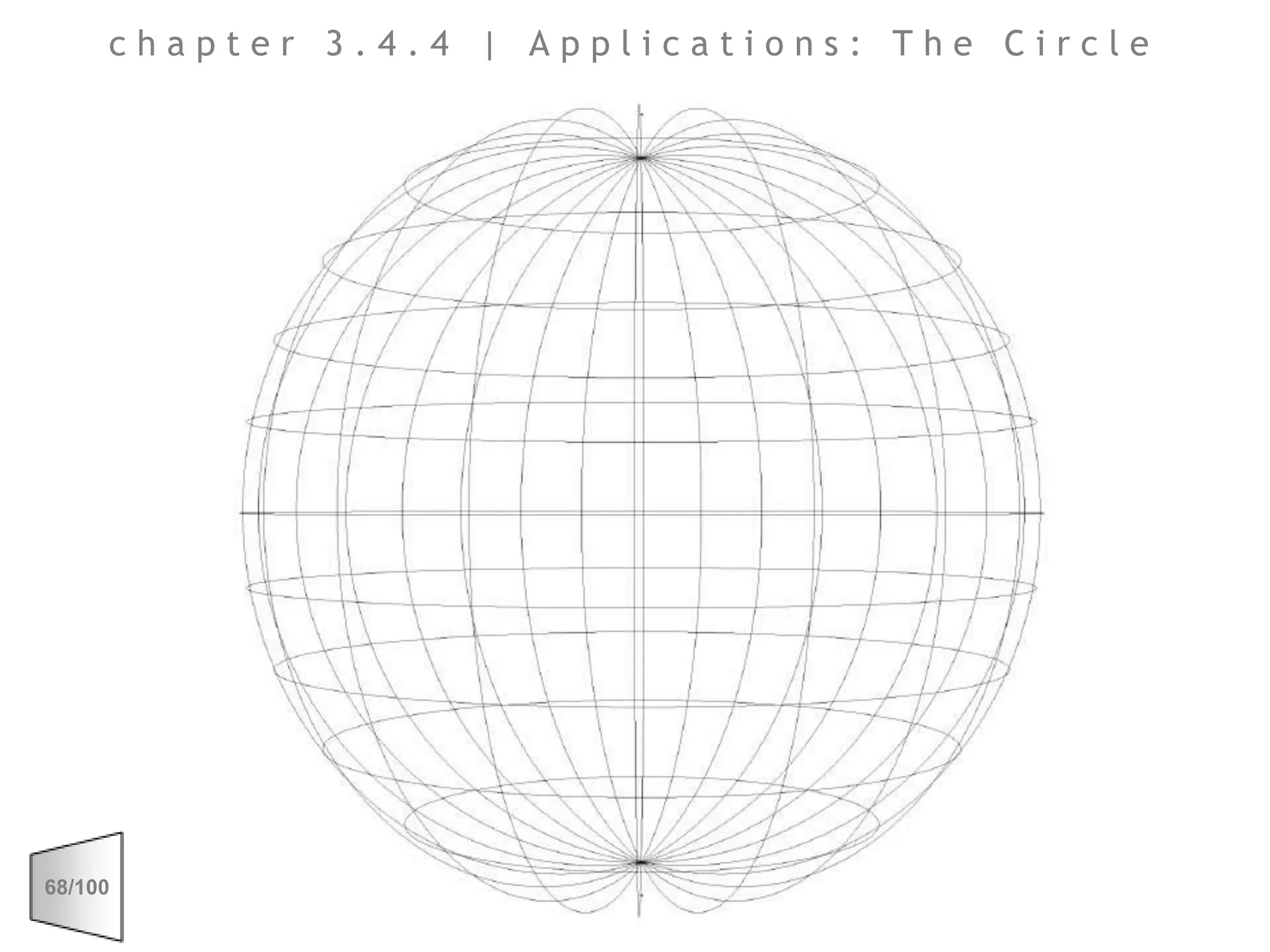
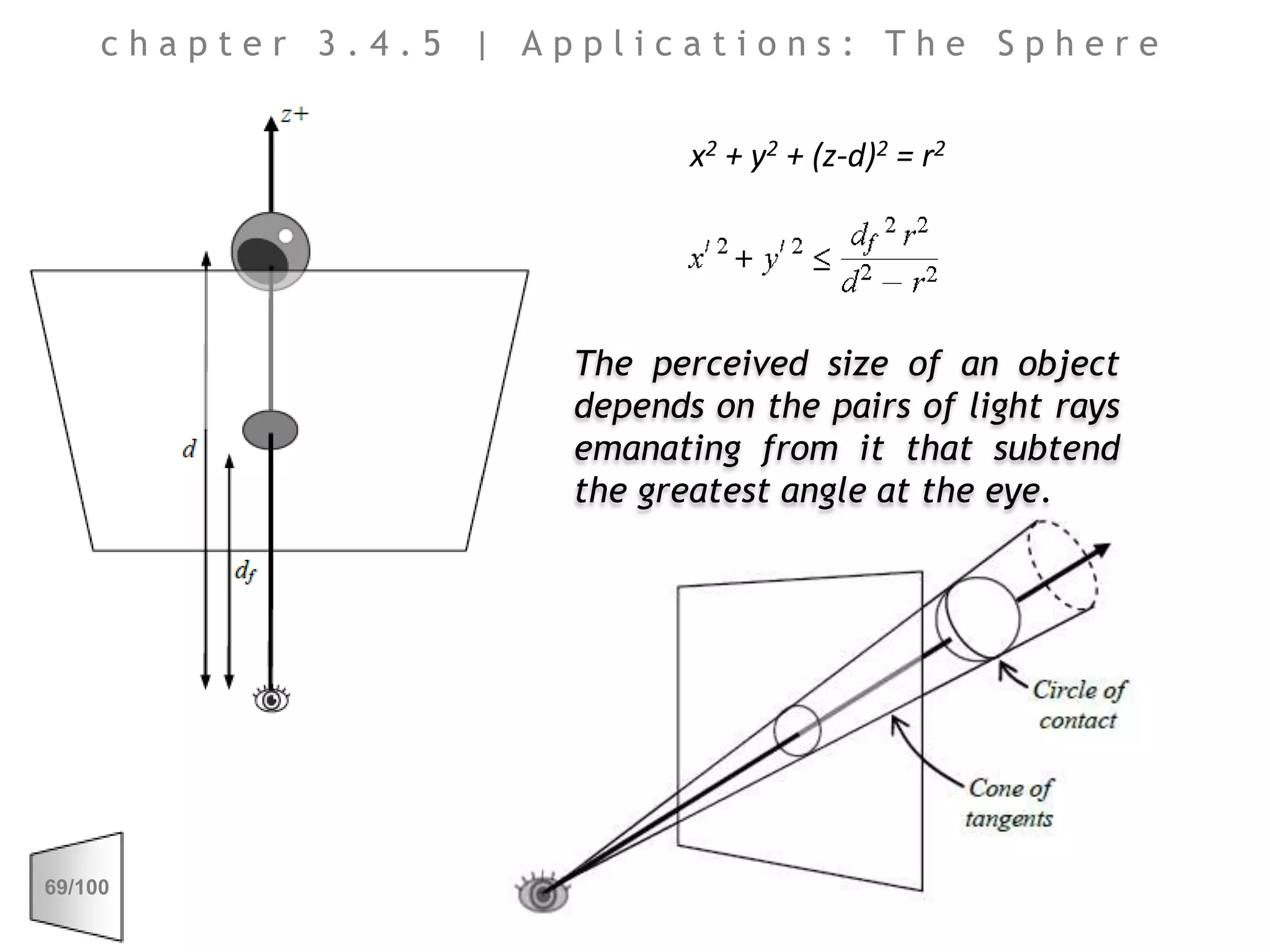
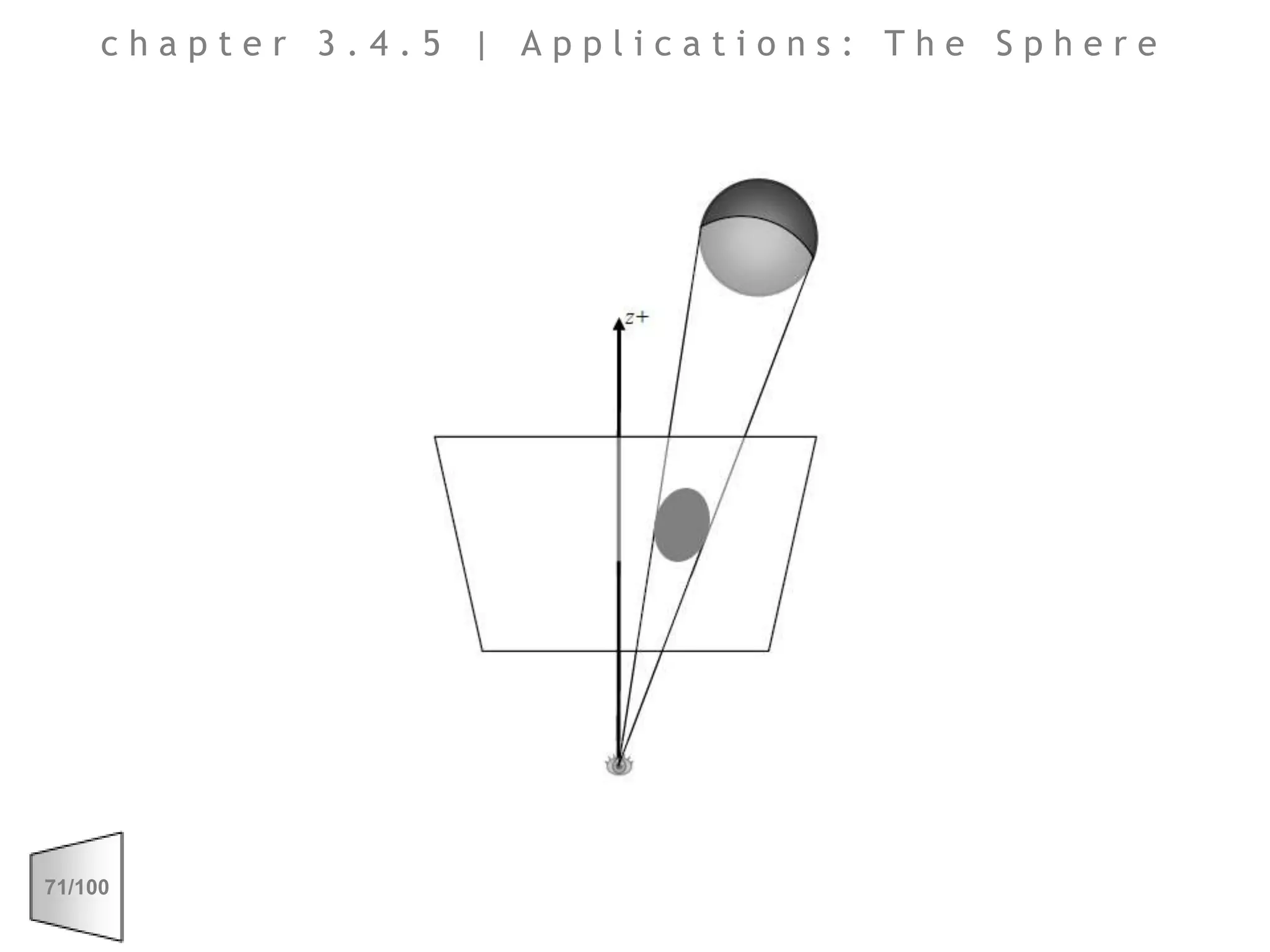
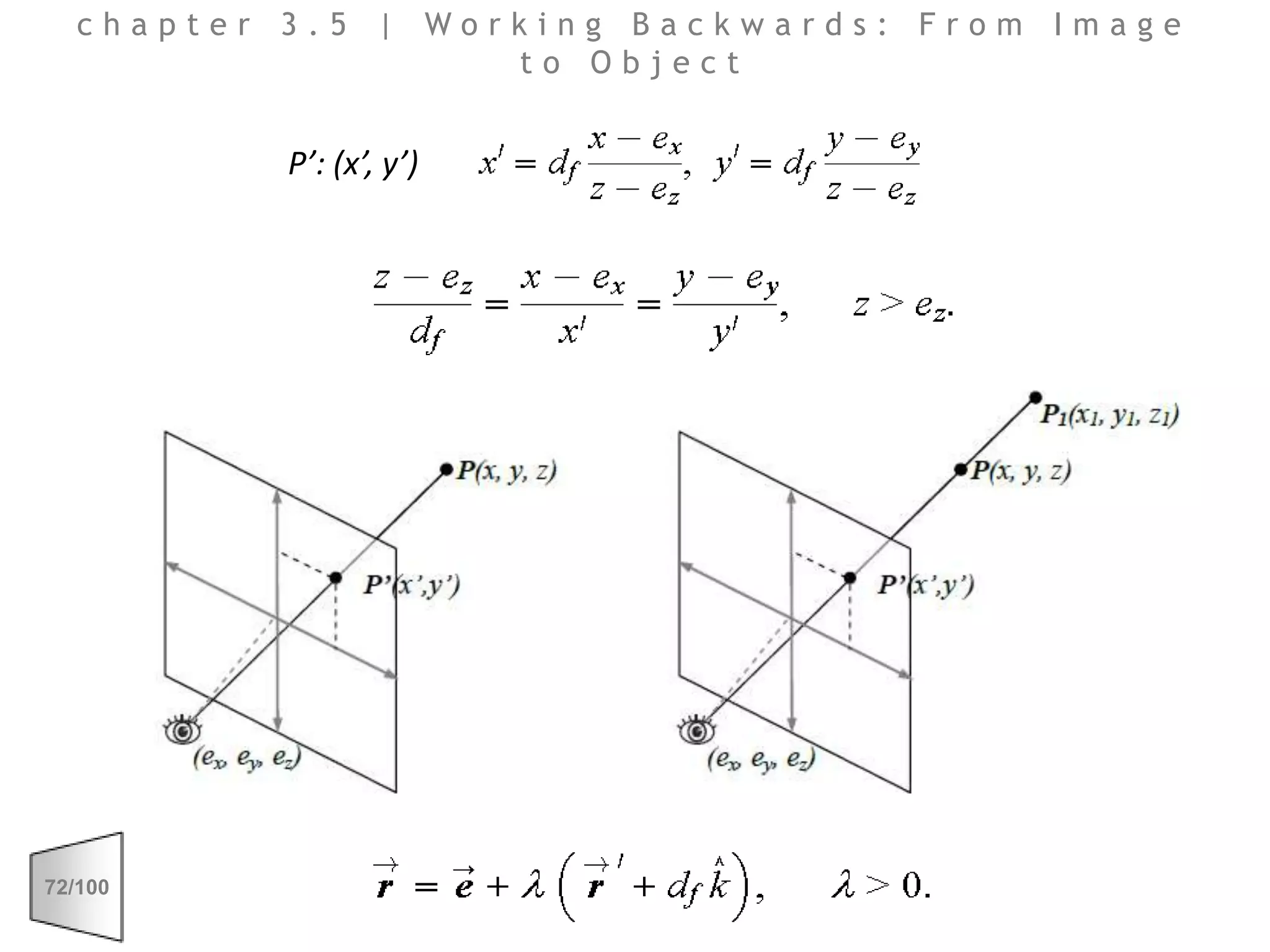
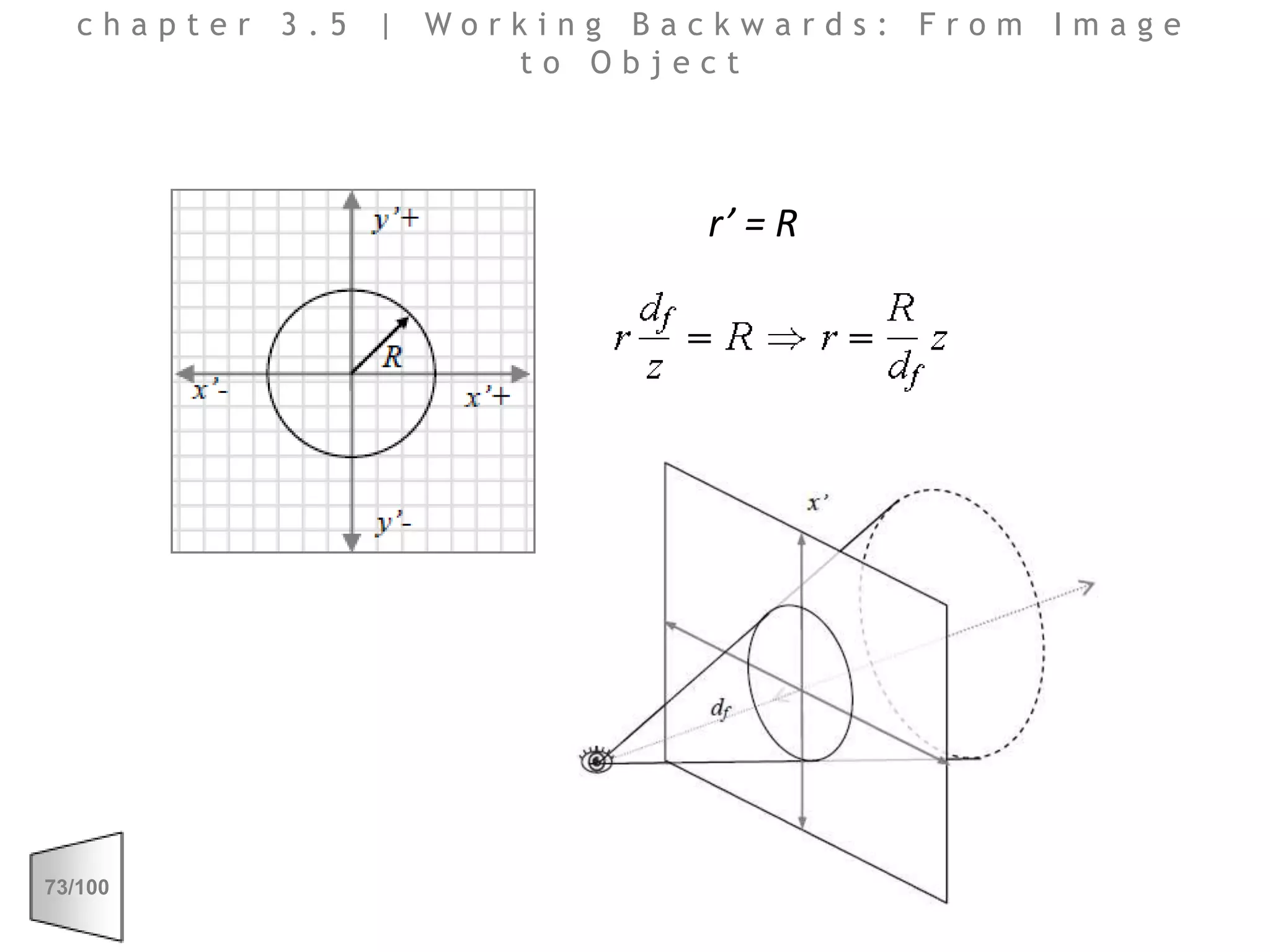
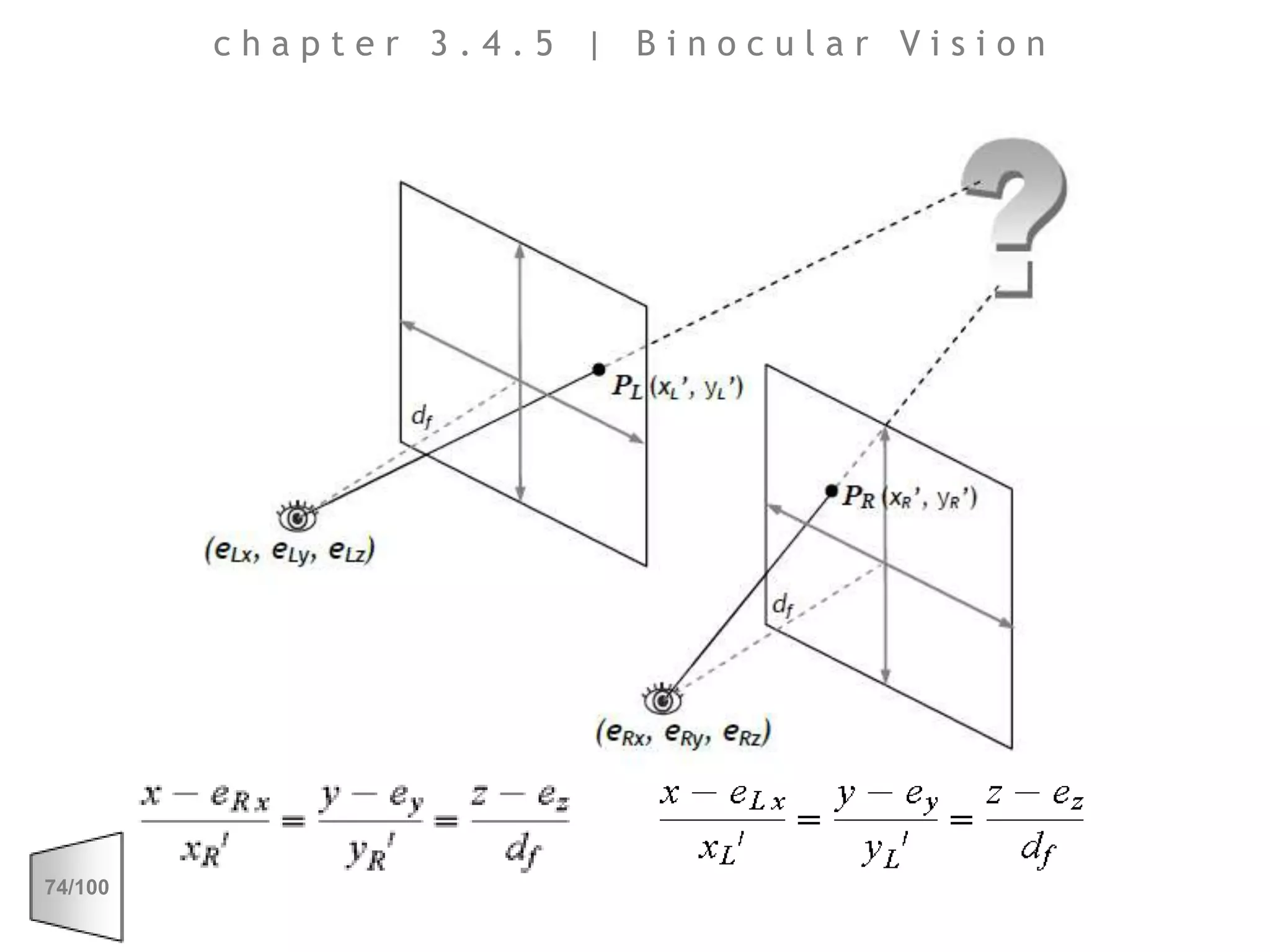
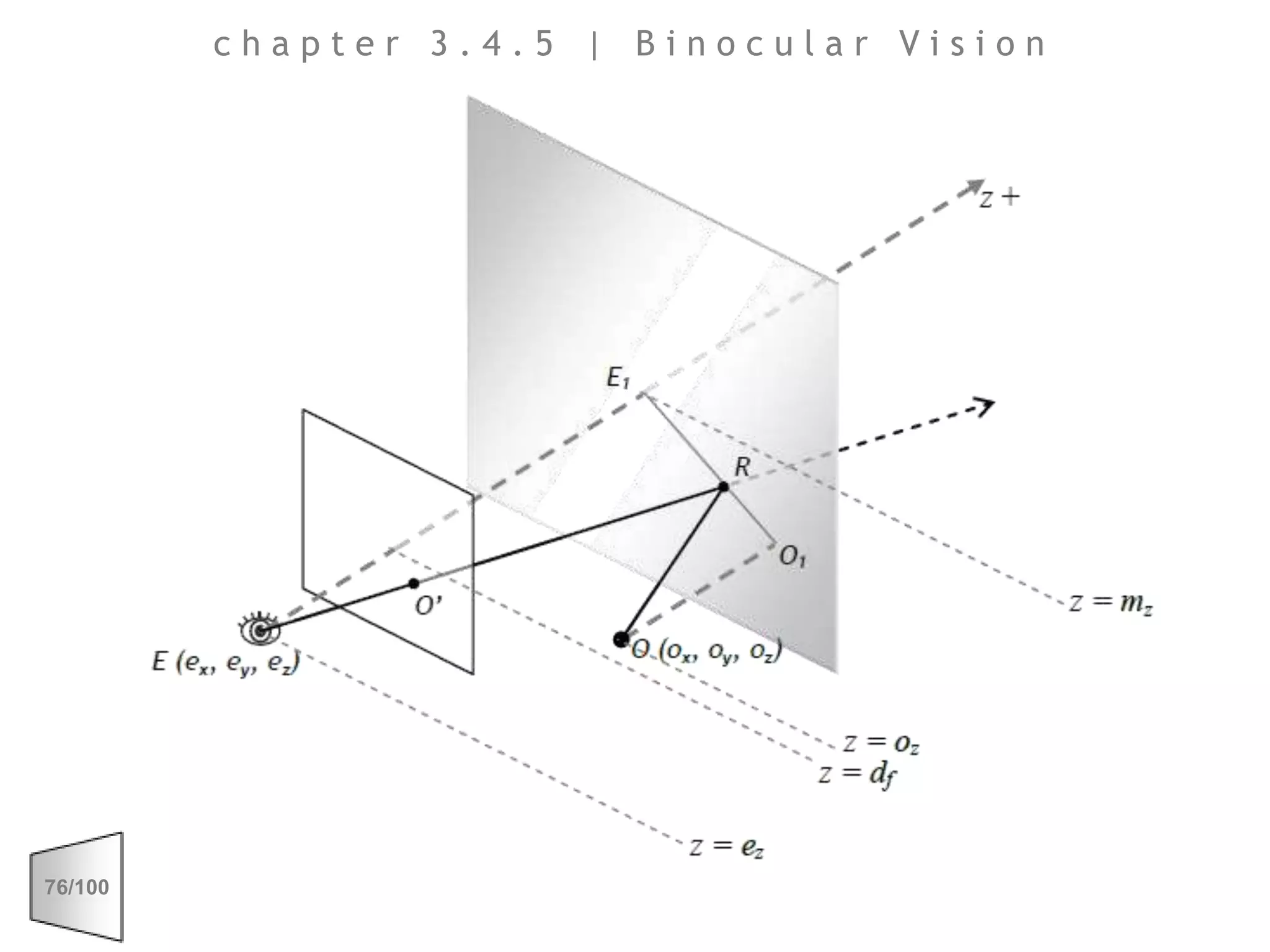
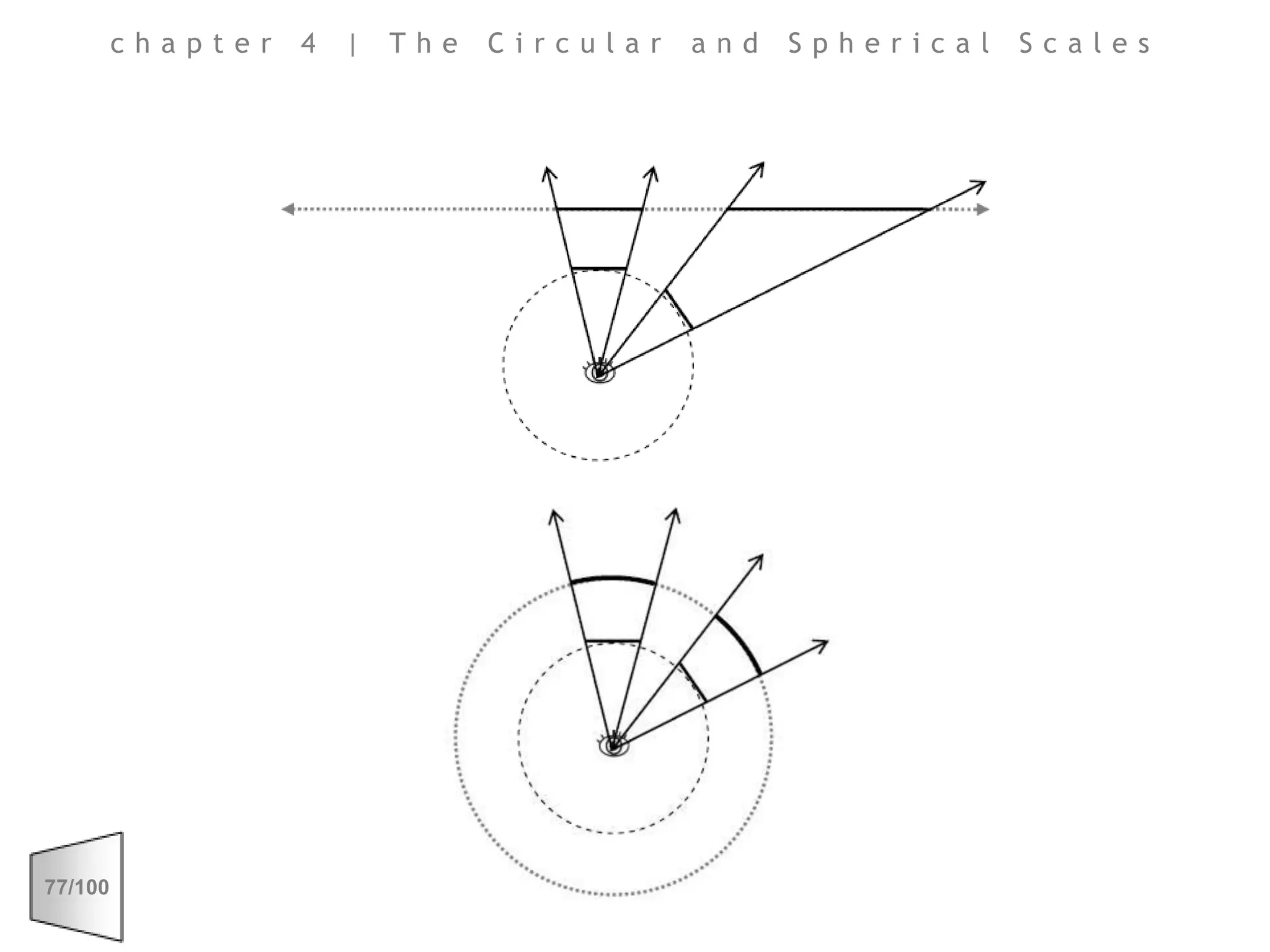
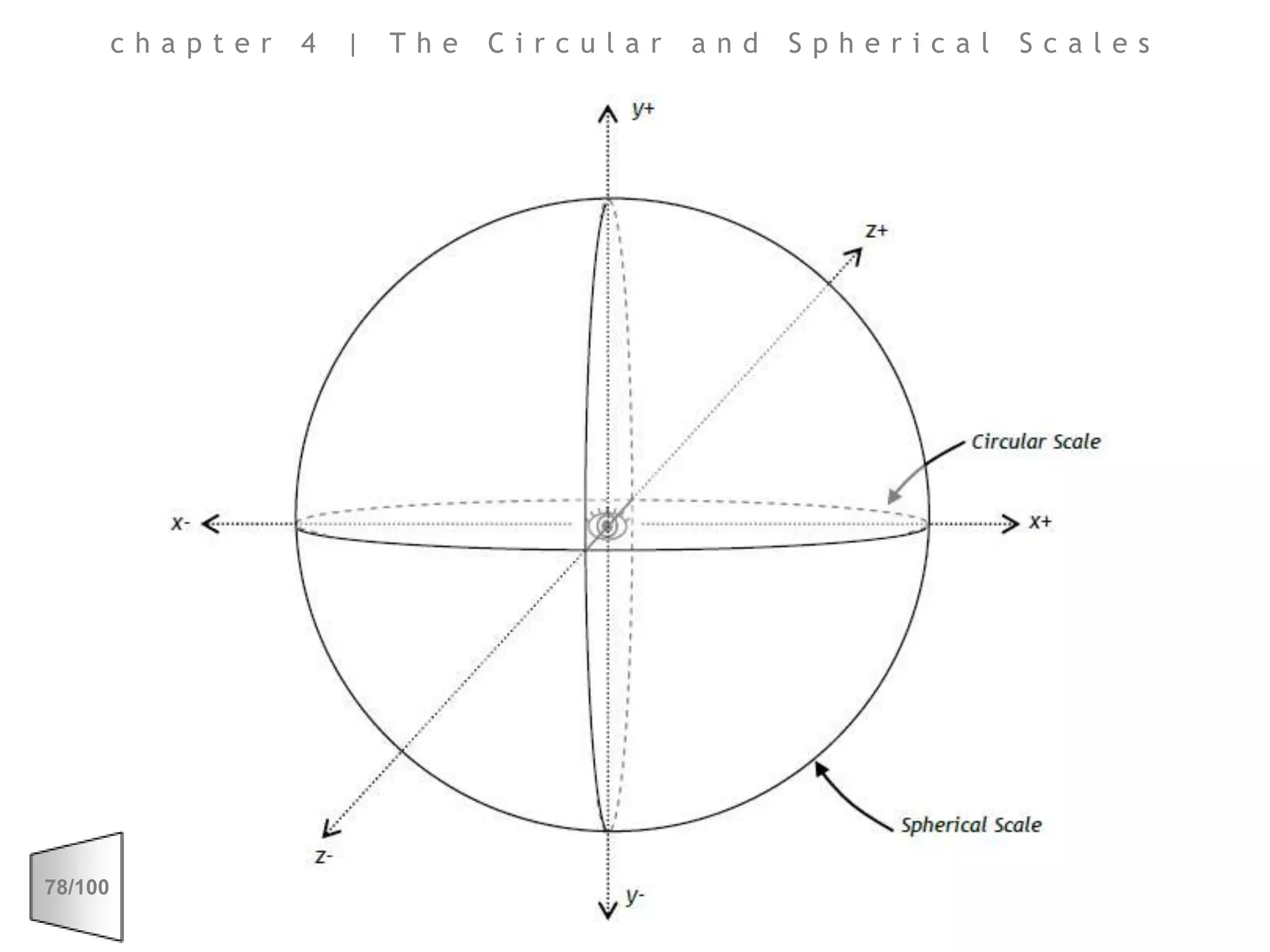
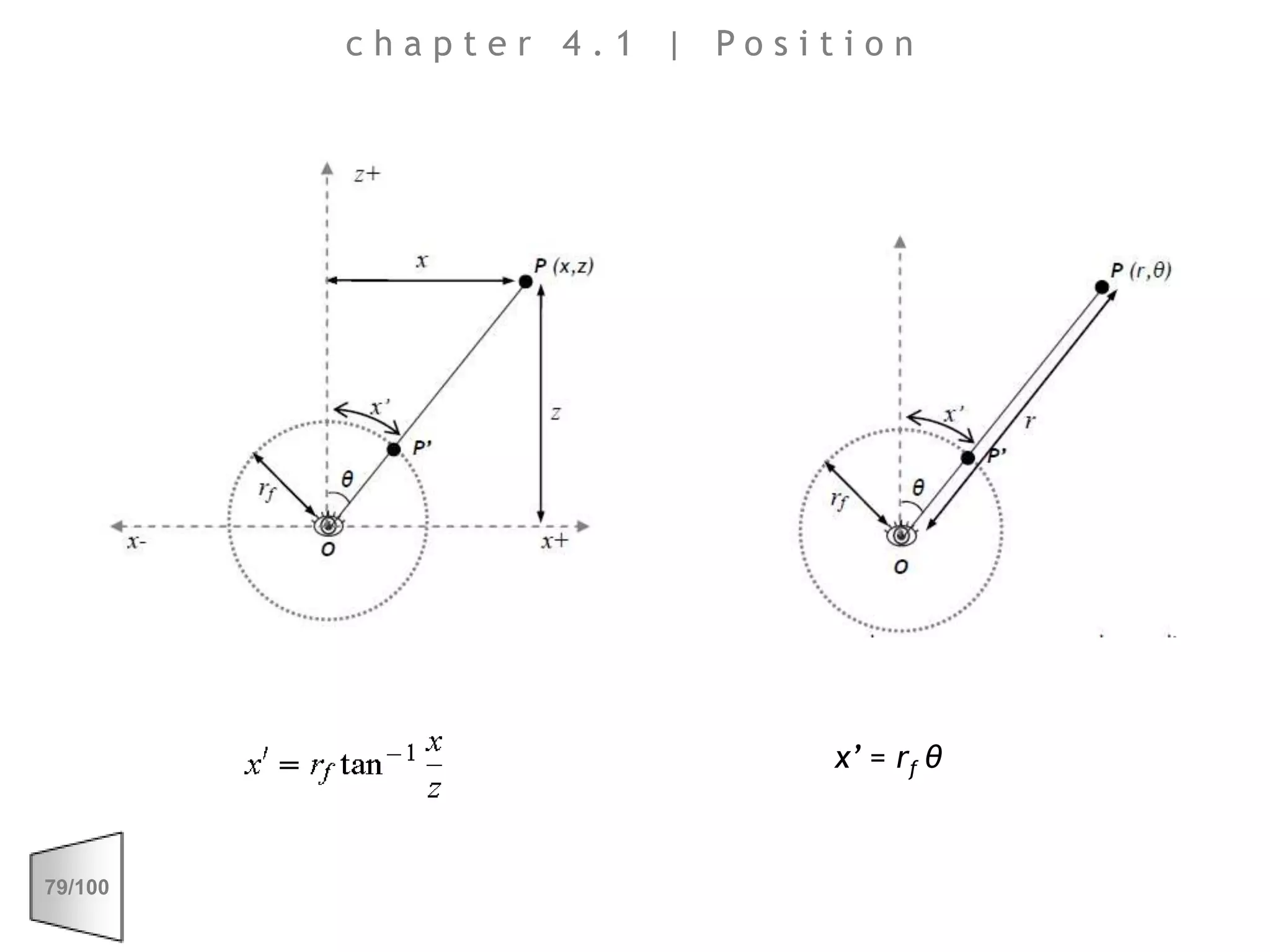
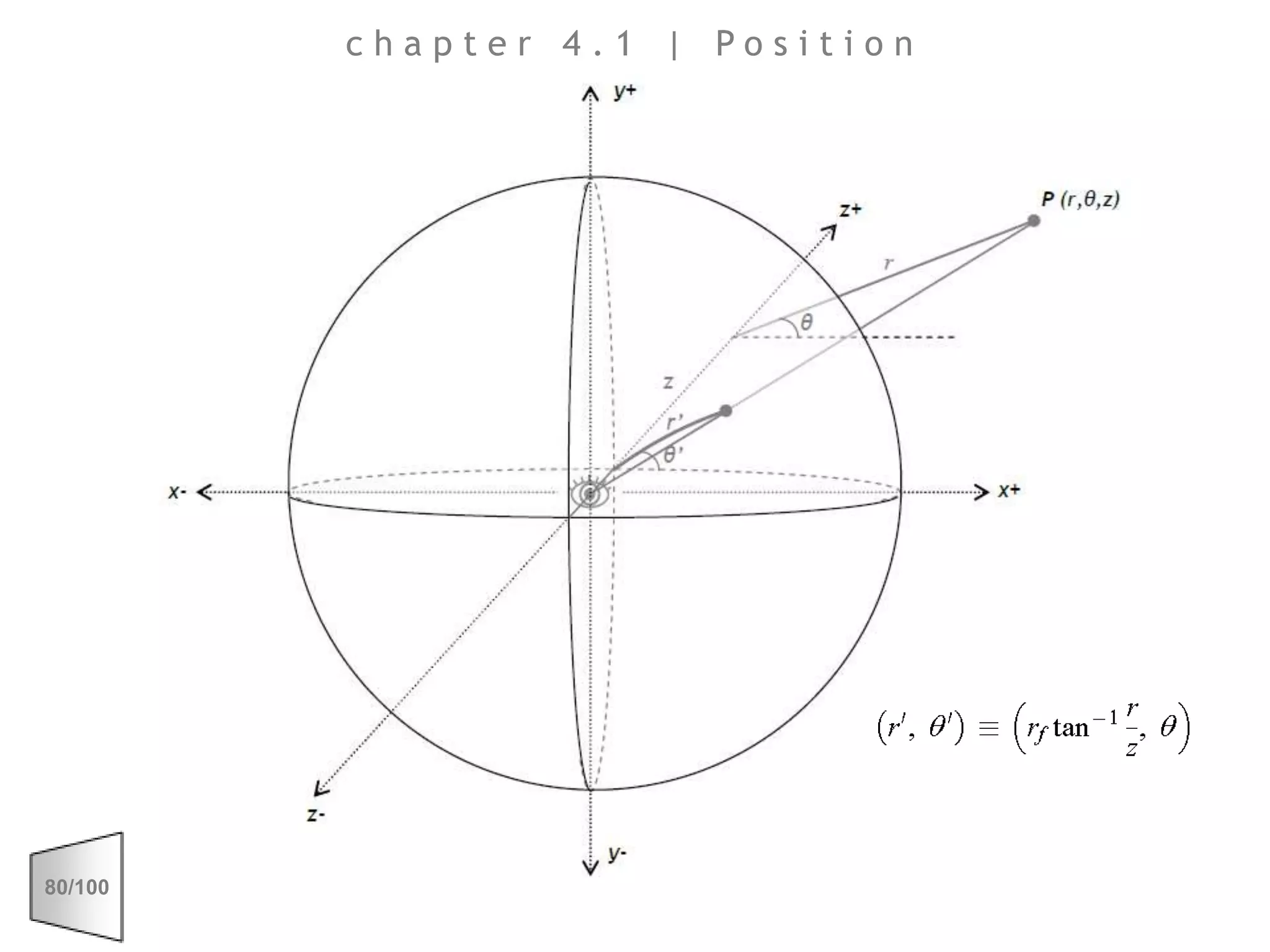
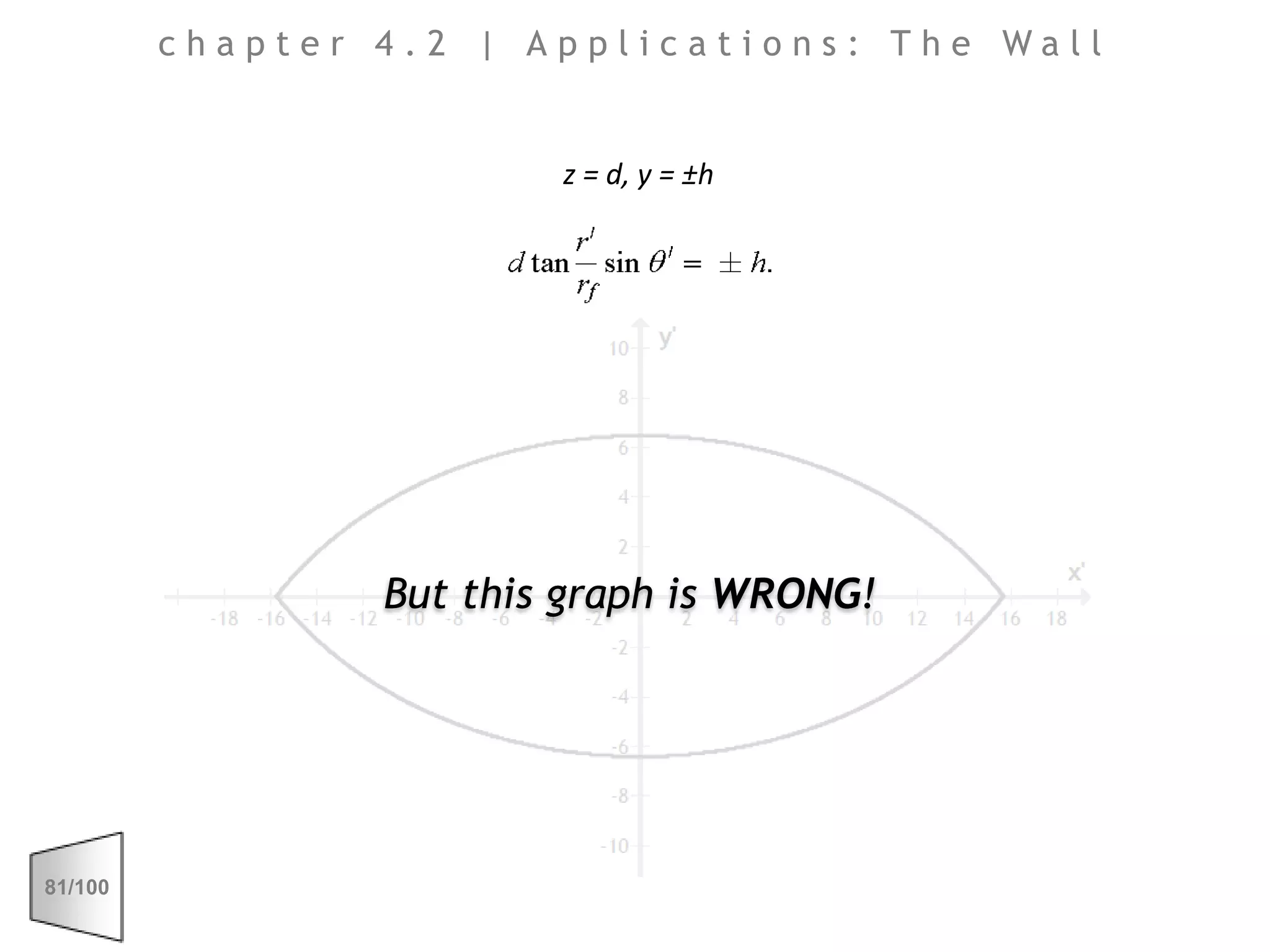
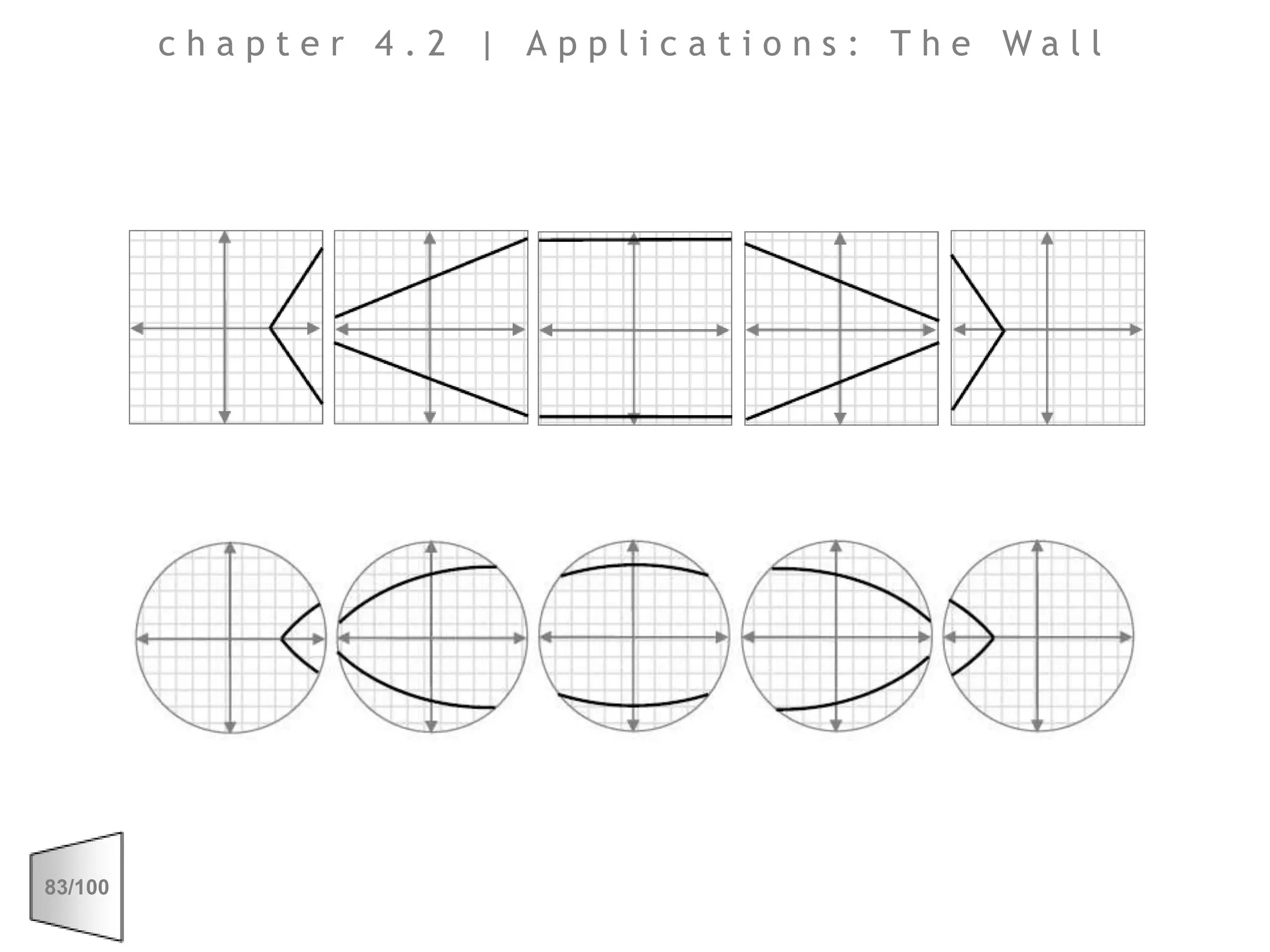
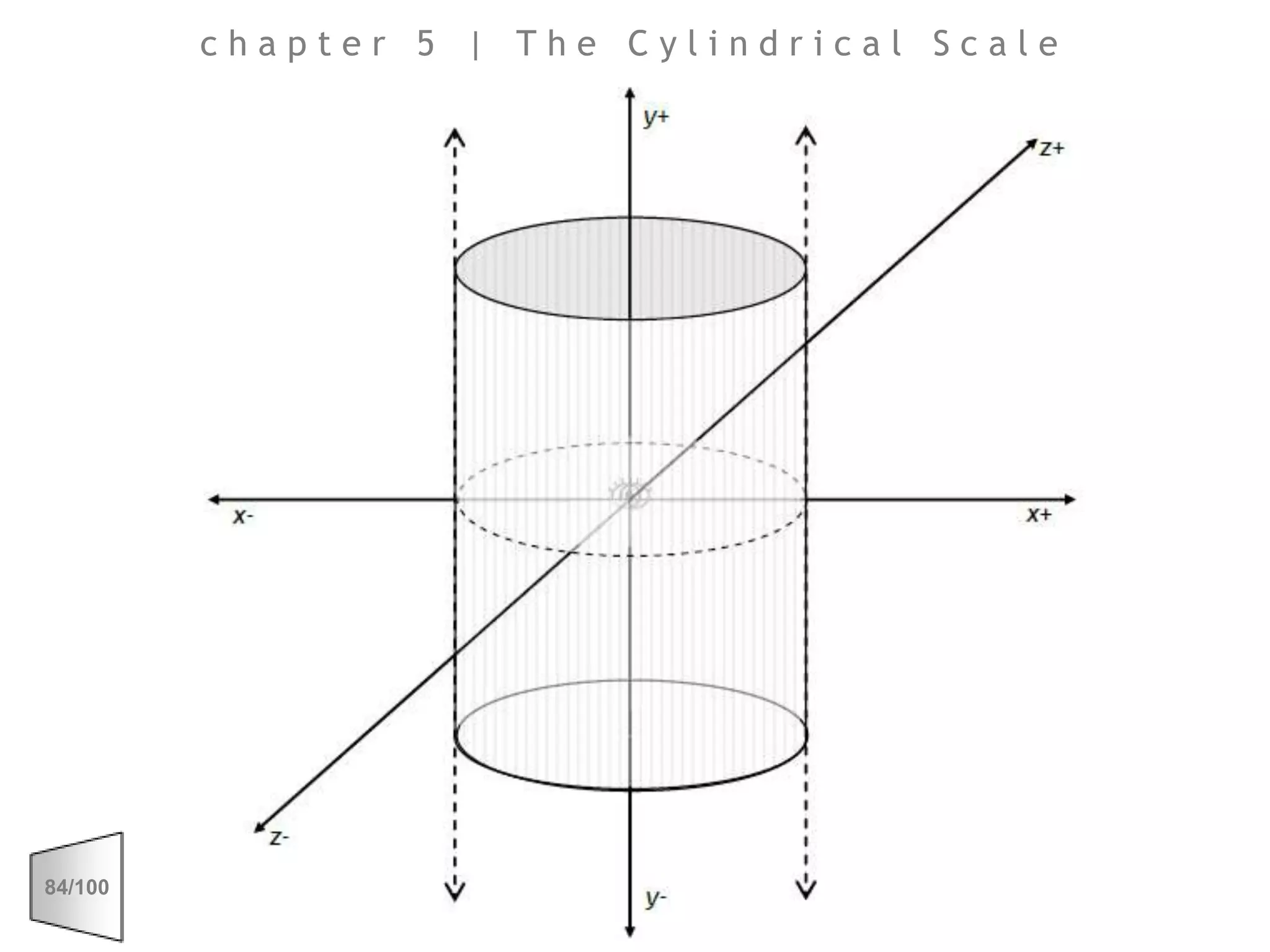
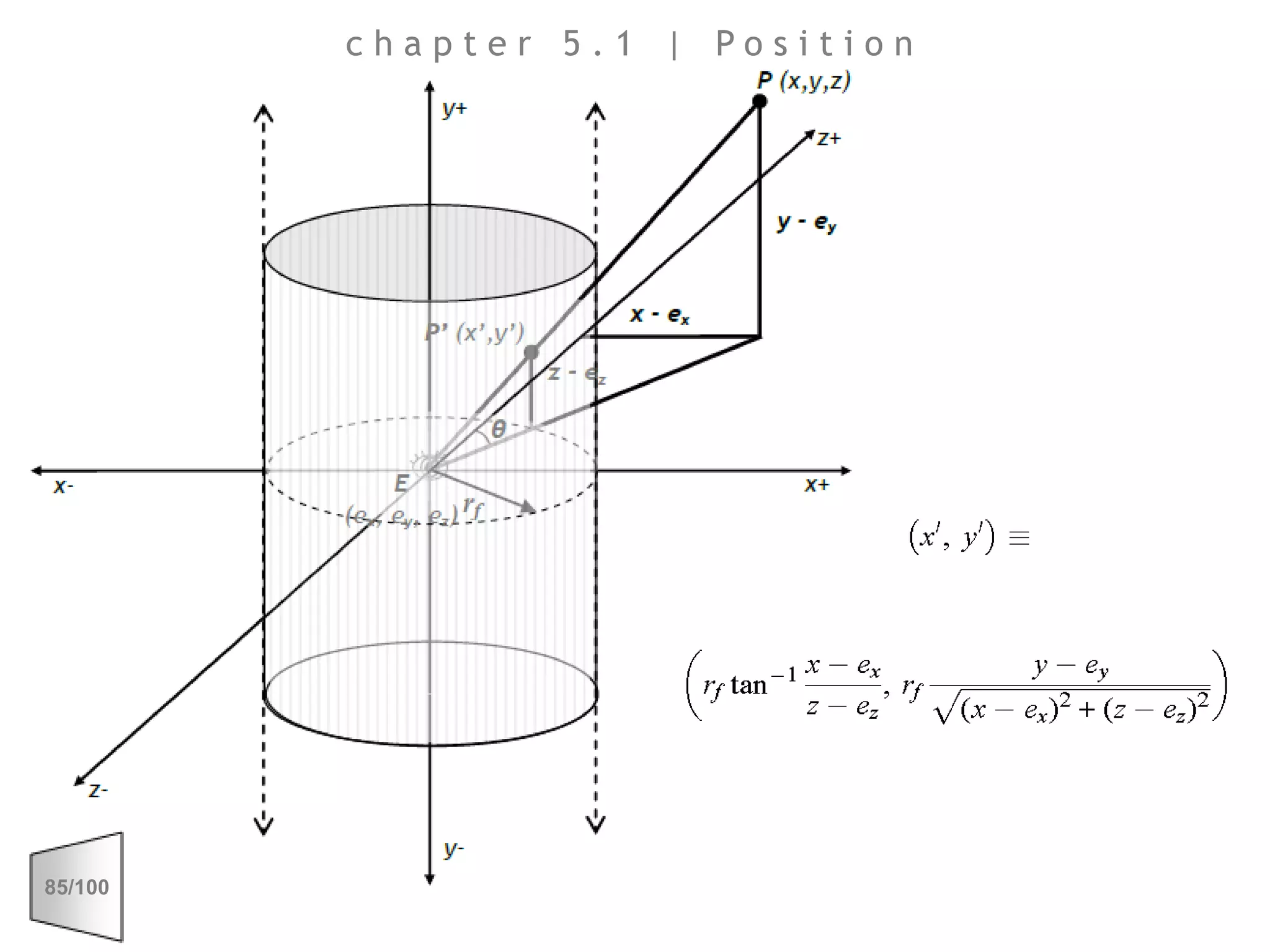
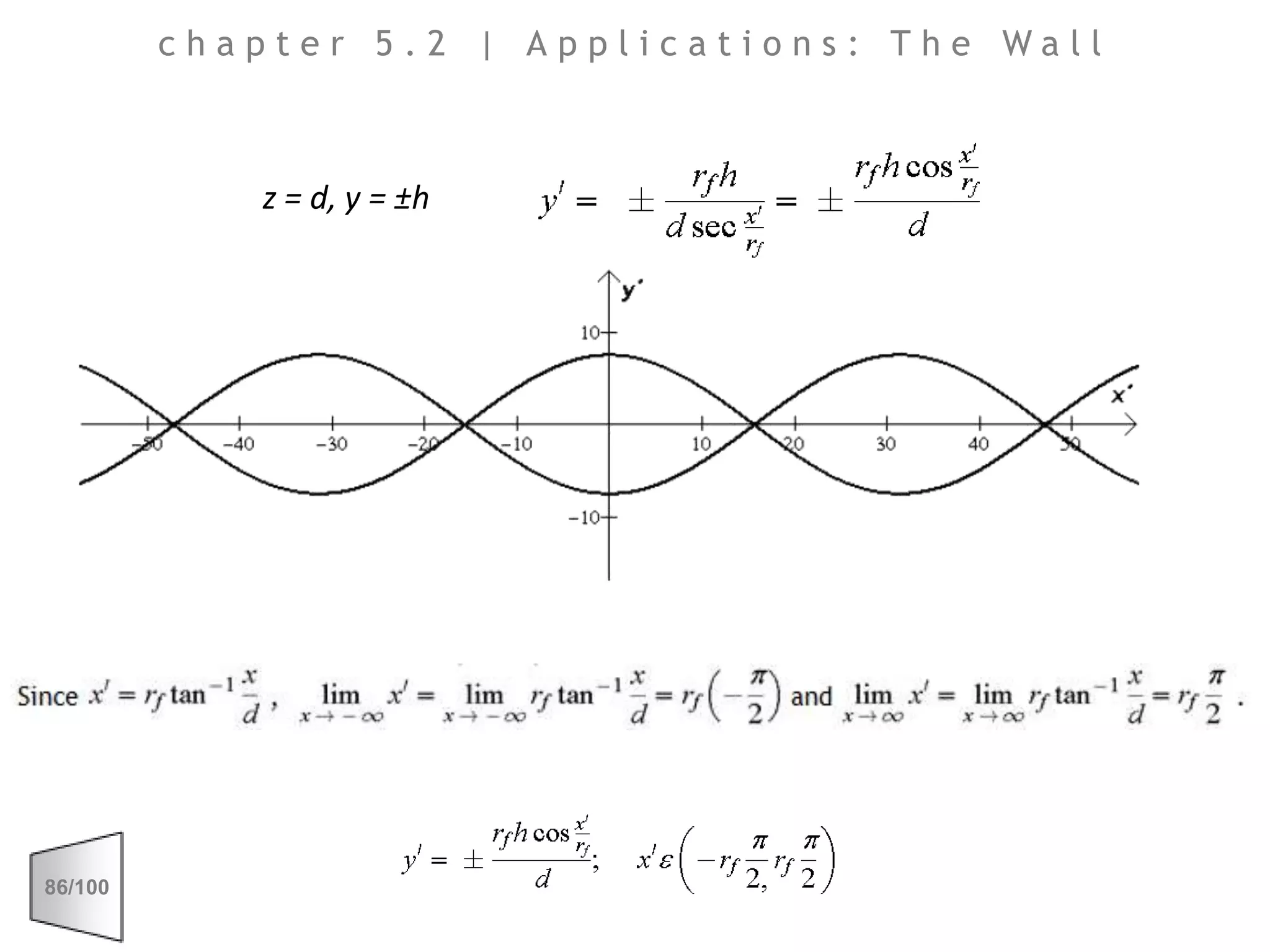
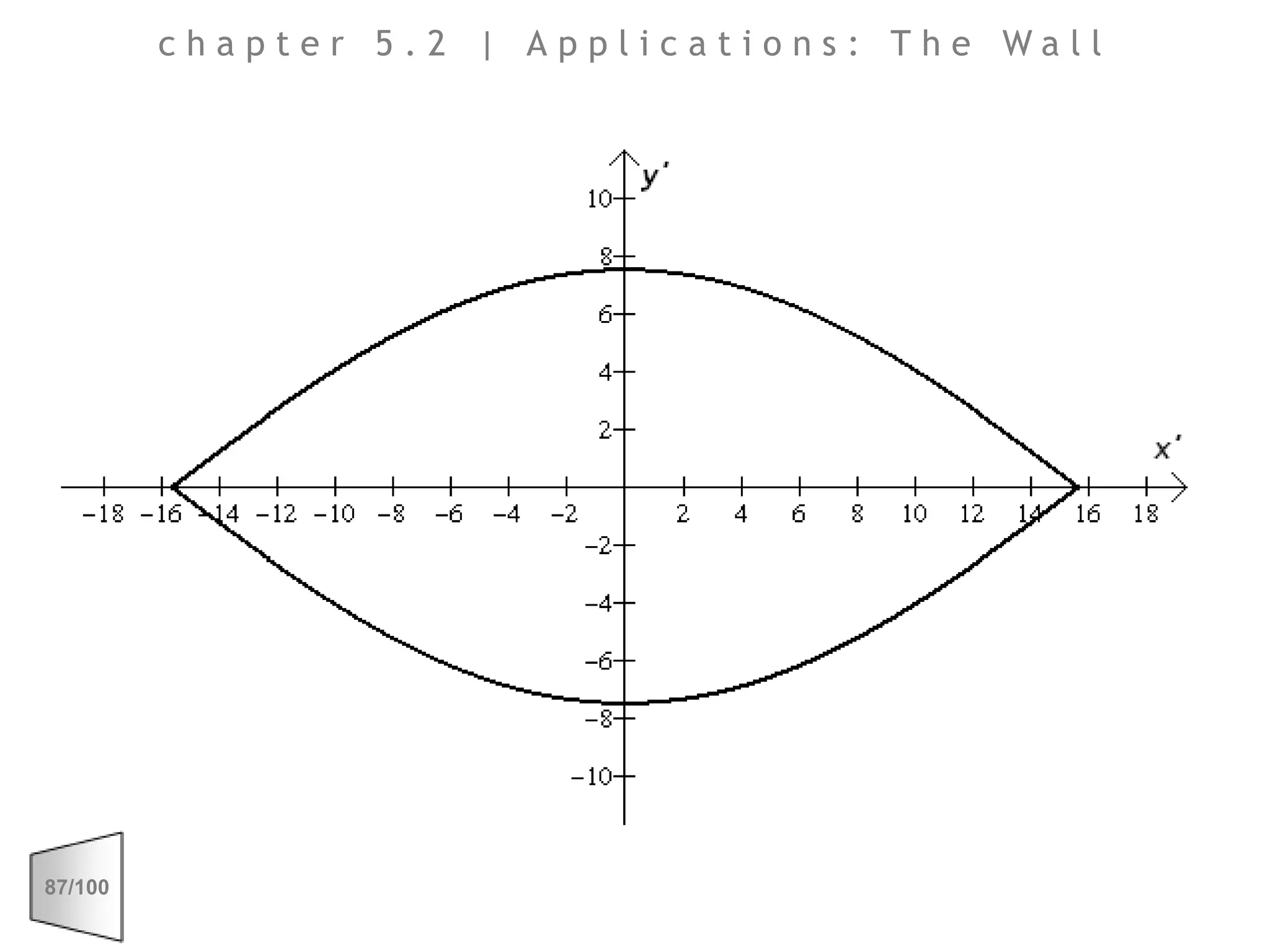
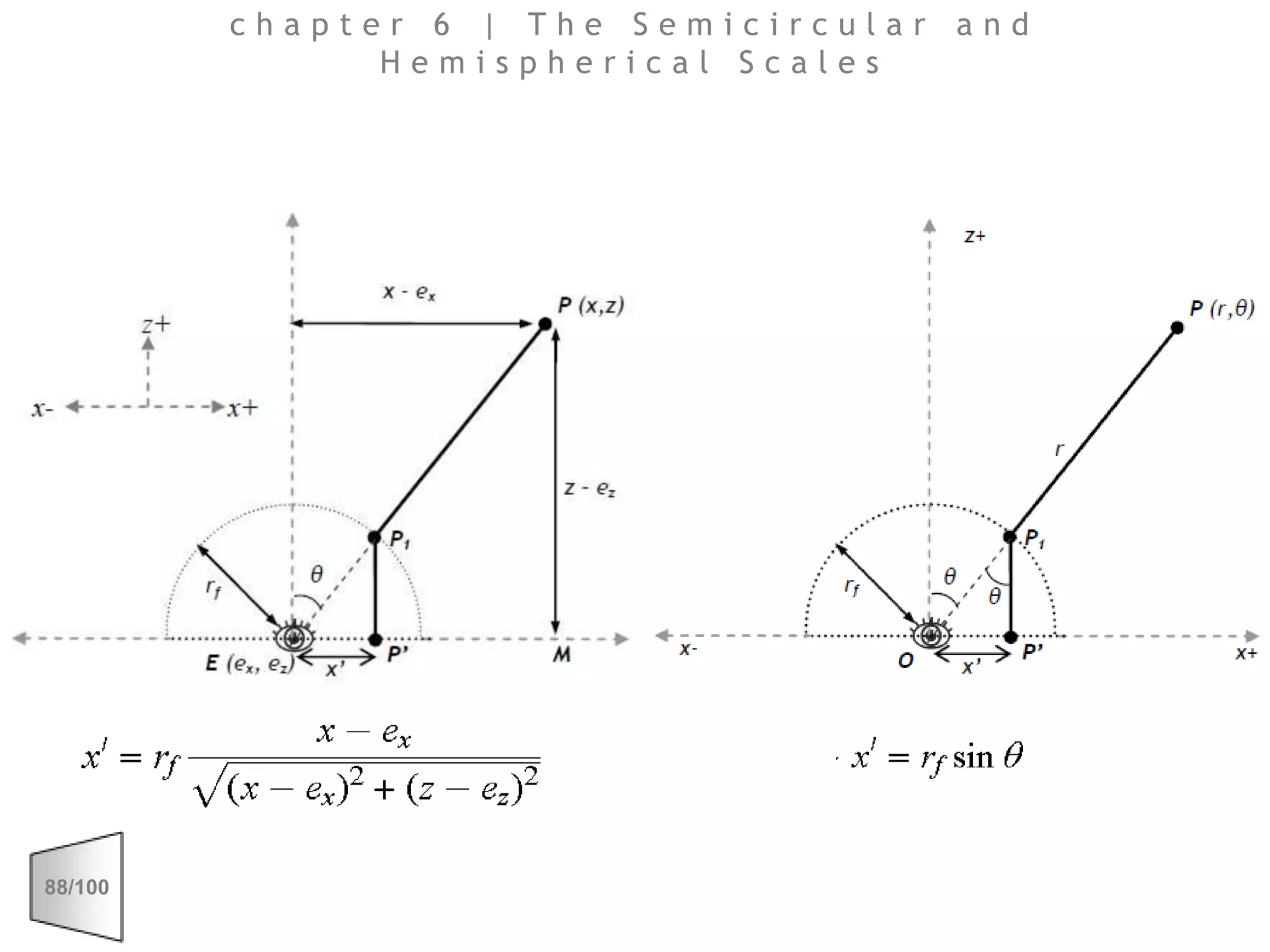
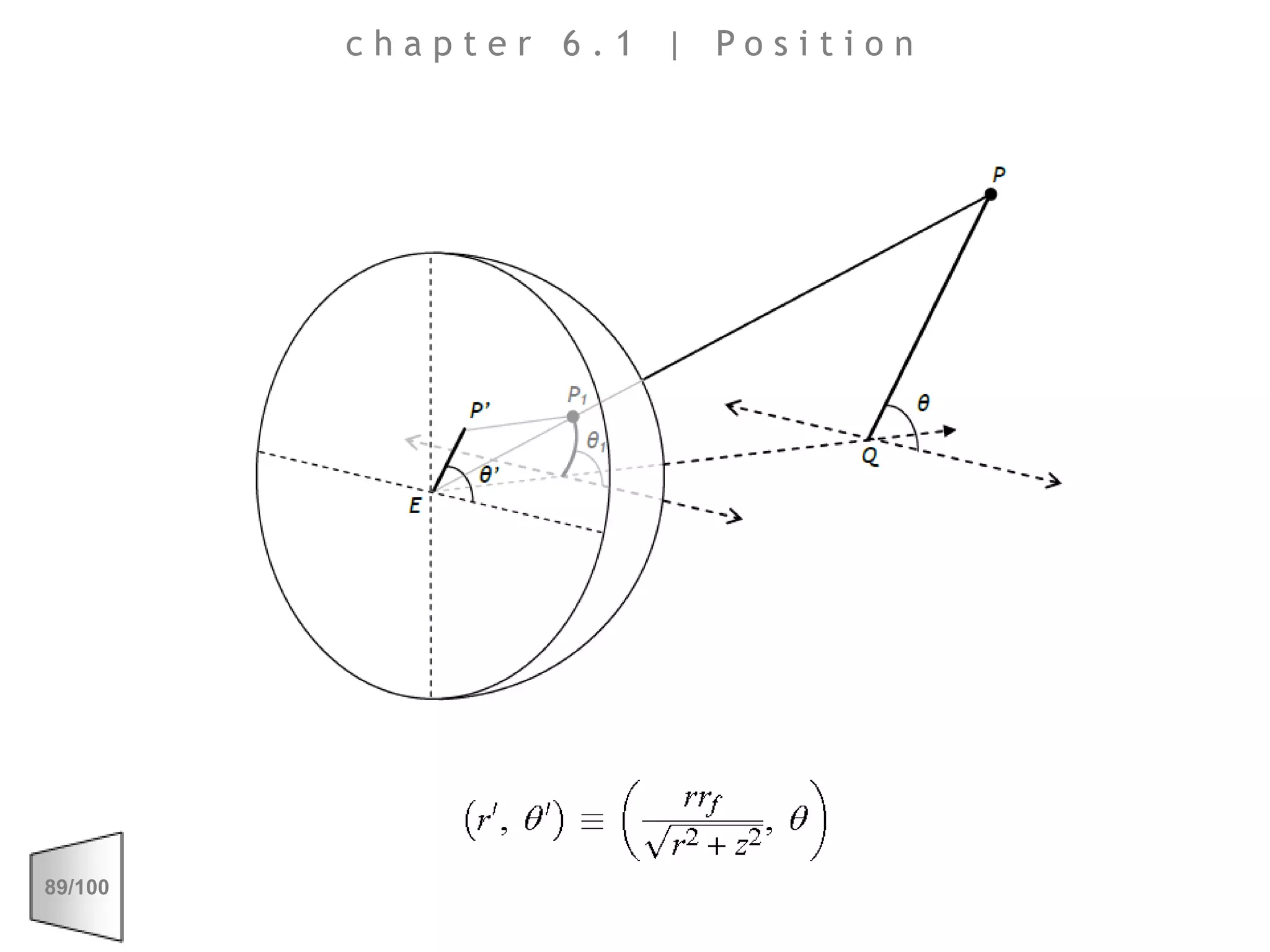
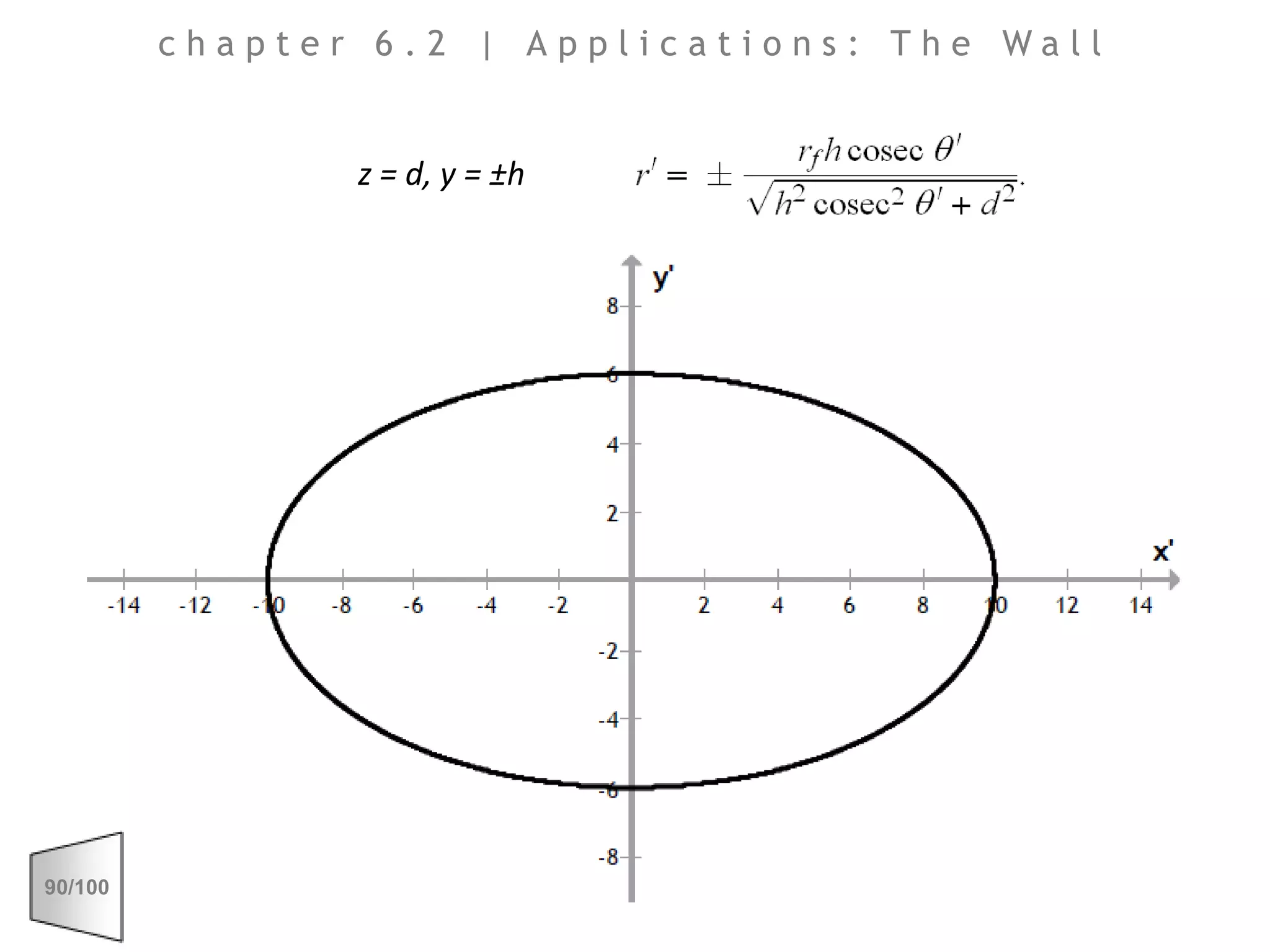
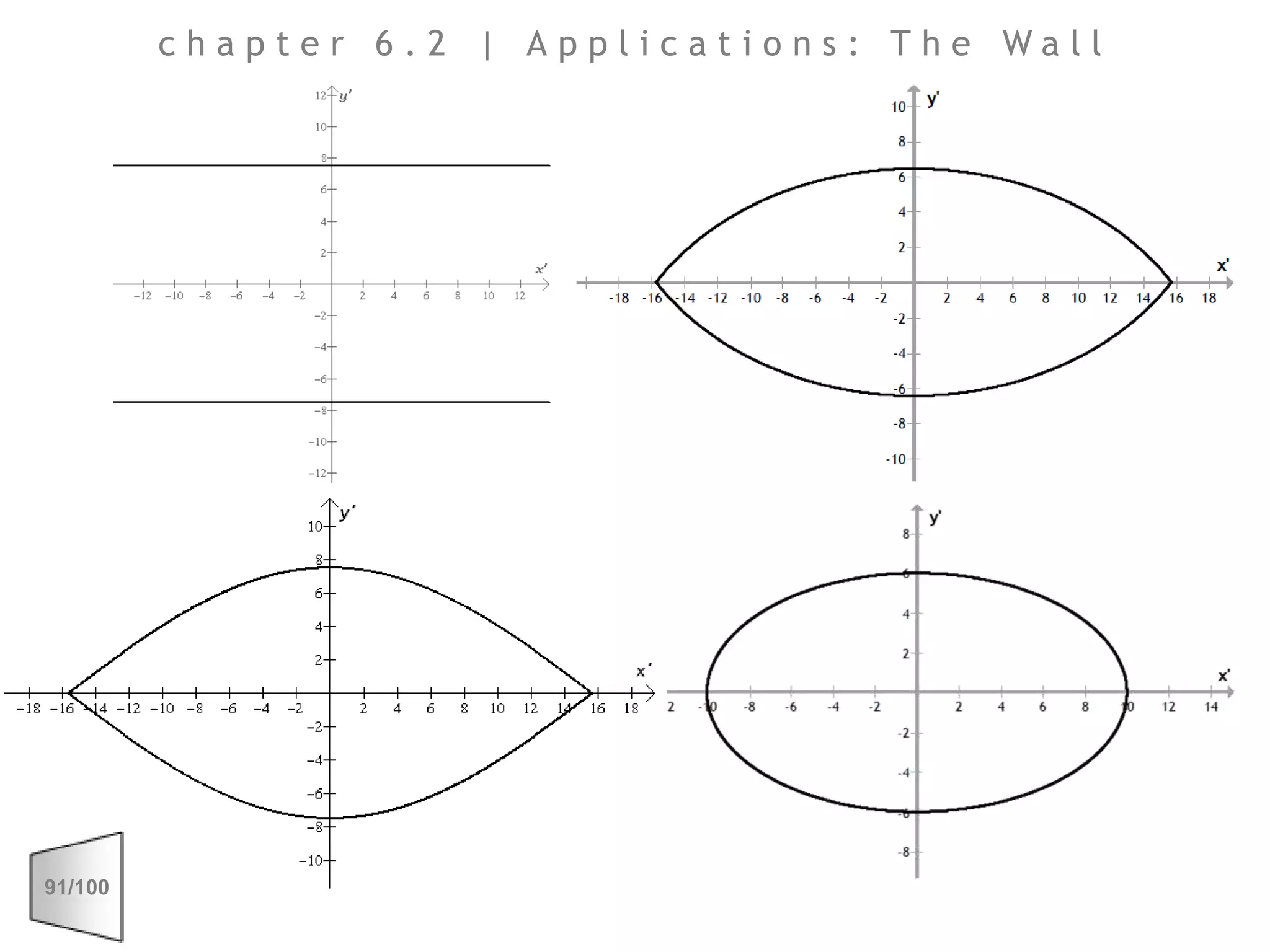
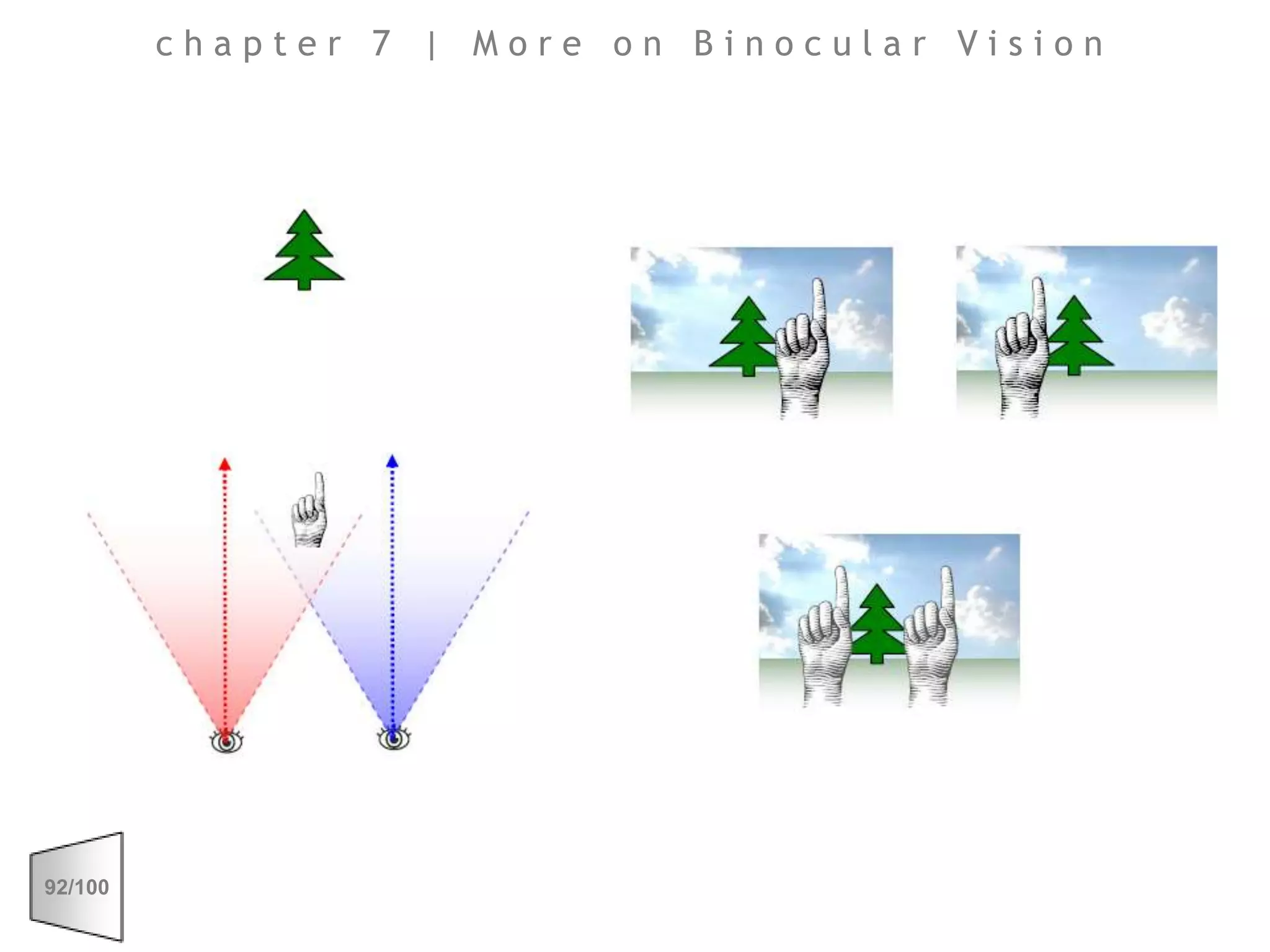
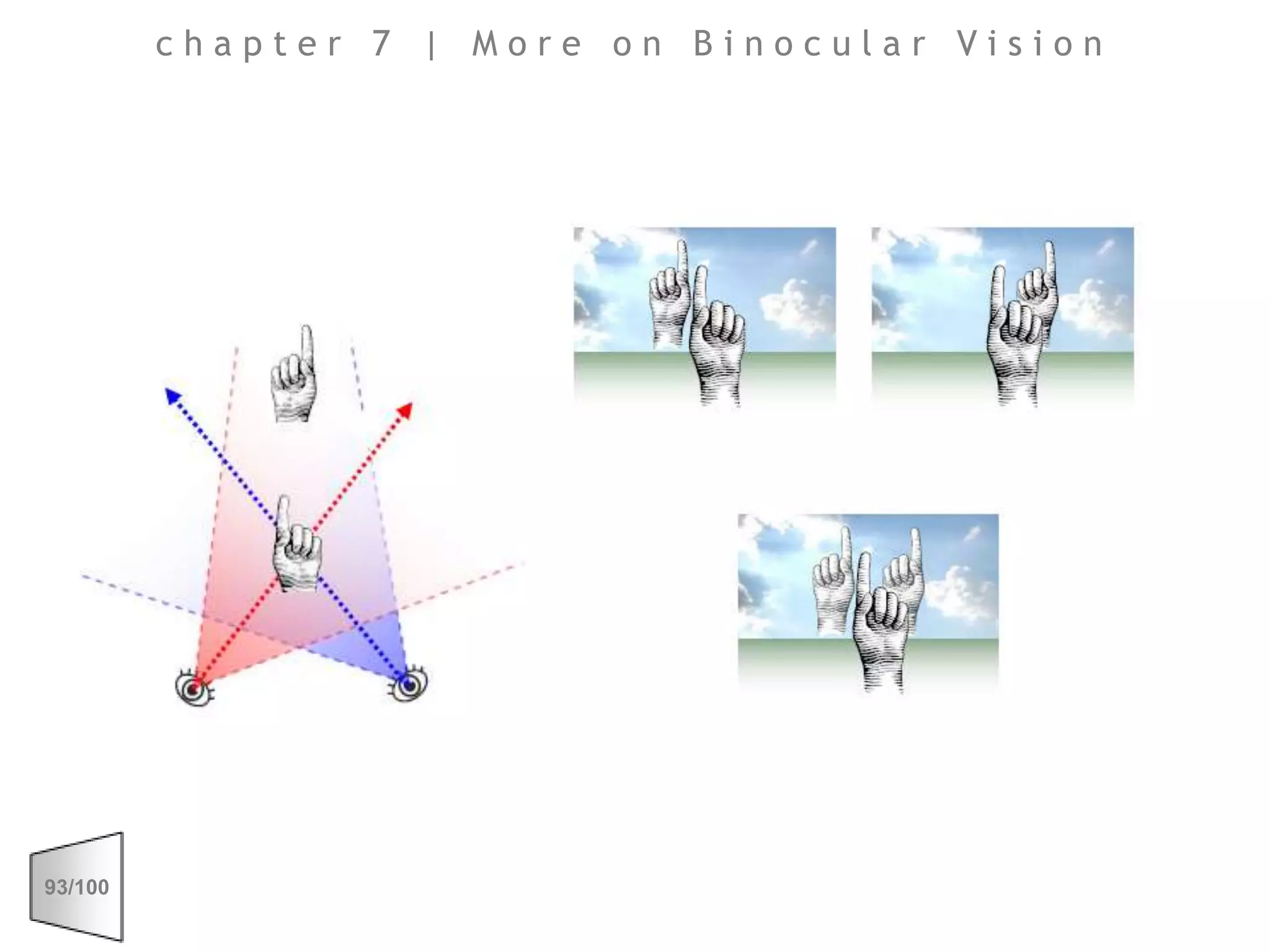
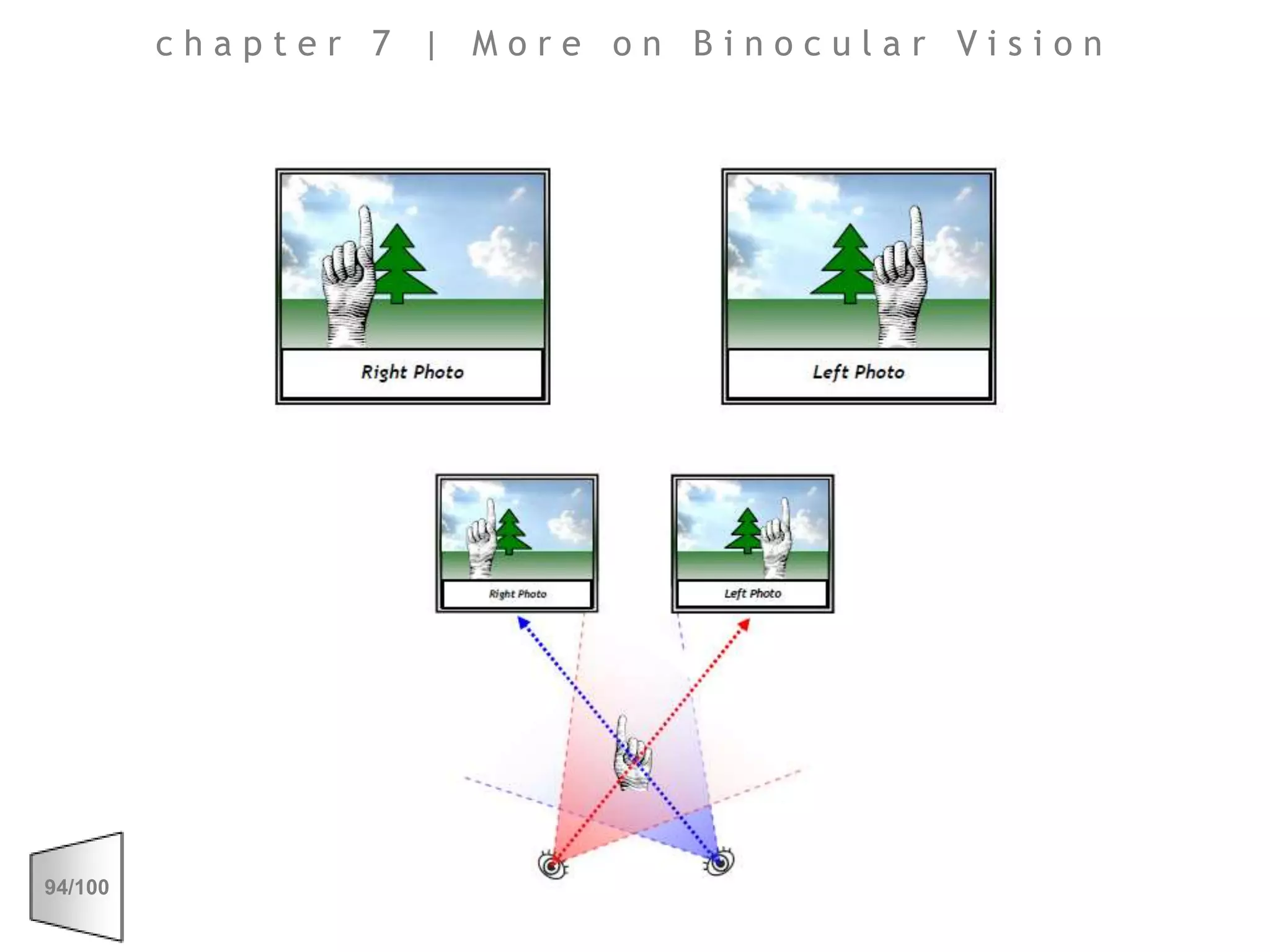
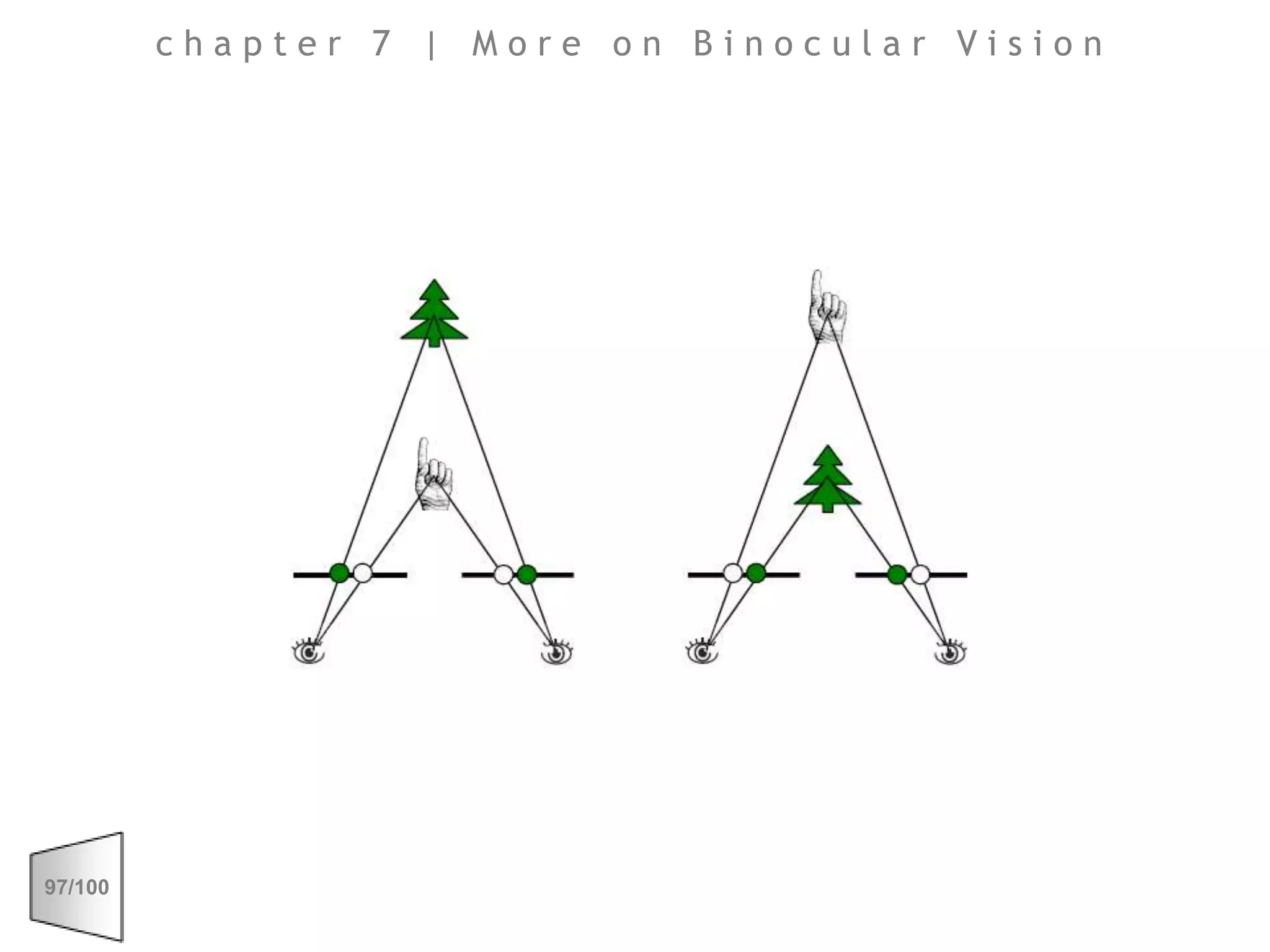
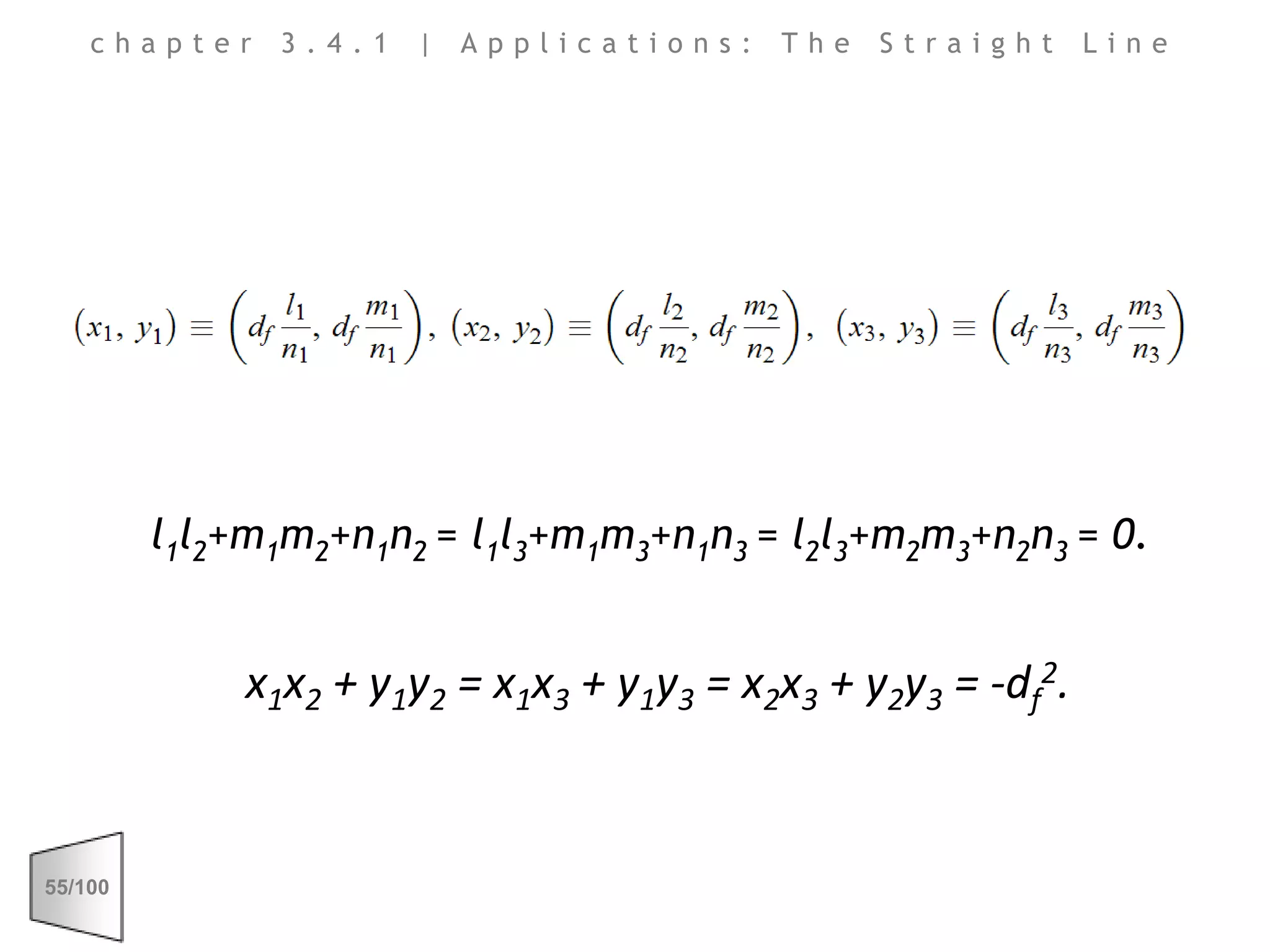This document discusses the principles of perspective and visual perception, emphasizing how the perceived size and position of objects depend on the angles subtended at the eye rather than their actual dimensions or distances. It covers various geometric applications, including linear, circular, and spherical scales, and explores concepts like collinearity, motion, and binocular vision. The text also addresses practical applications of these principles in contexts such as projecting objects and visualizing geometrical shapes.

2. chapter 1 | The Necessity of Perspective

3. chapter 1 | The Necessity of Perspective

4. chapter 2 | Collinearity and Angle

5. chapter 2 | Collinearity and Angle

6. chapter 2 | Collinearity and Angle

7. chapter 2 | Collinearity and Angle

8. chapter 2 | Collinearity and Angle

9. chapter 2 | Collinearity and Angle

10. In a given plane, the perceived length of an object depends on the pair of light rays emanating from the two points of the object in that plane that subtend the greatest angle at the eye. chapter 2 | Collinearity and Angle

11. chapter 2 | Collinearity and AnglePoints that are collinear with the eye will appear to share the same position, and hence, appear to be the same point.

12. The apparent dimension of an object does not depend directly on what its actual dimension is, nor at what distance from the eye it is placed. It depends directly on one, and only one thing: the angle subtended by it at the eye. The larger this angle compared to the angles of other objects, the larger it will look compared to them.chapter 2 | Collinearity and Angle

13. chapter 3 | The Linear and Planar Scales

14. chapter 3 | The Linear and Planar Scales

15. chapter 3 | The Linear and Planar Scales

16. chapter 3 | The Linear and Planar Scales

17. chapter 3 | The Linear and Planar Scales

18. chapter 3 | The Linear and Planar Scales

19. chapter 3 | The Linear and Planar Scales

20. chapter 3 | The Linear and Planar Scales

21. chapter 3 | The Linear and Planar Scales

22. chapter 3 | The Linear and Planar Scales

23. chapter 3.1 | Size

24. chapter 3.1 | Size

25. There’s a car whose breadth is 2 meters, and you hold a scale about 10 cm from your eye. 100 m away, 1 m away,10,000 times!chapter 3.1 | Size

26. chapter 3.1 | Sizel’∝ df

27. chapter 3.1 | Size

28. chapter 3.1 | Size5.1 mm, 1 m away

29. chapter 3.1 | Sizen∆l, n∆l’

30. chapter 3.1 | Size

31. chapter 3.1 | Size

32. chapter 3.2 | Position

33. chapter 3.2 | PositionIn ΔOP’N’, tanθ = x’/df⇒x’ =dftanθ.

34. chapter 3.2 | Position

35. chapter 3.2 | Position

36. chapter 3.2 | Positionθ’ = θ.

37. ?chapter 3.2 | Position(r’, θ’) ≡But the vanishing point is not always at the centre, along our line of sight.

38. chapter 3.2 | PositionUse this with functions f(x,y,z,t) to project objects at a single go.E = E(t)

39. chapter 3.2 | Position

40. chapter 3.2 | Position

41. chapter 3.3 | MotionFor non-planar displacements, project end-points, then join.

42. chapter 3.3 | Motion

43. chapter 3.3 | Motion

44. chapter 3.3 | Motion

45. Review of Part 1

46. Review of Part 1

47. chapter 3.4.1 | Applications: The CubeA cube of side-length 50cmdx = 20cmdy = 30cmdz = 1mThe reference frame is at a distance df = 10cm, and graduated in meters.

48. chapter 3.4.1 | Applications: The Cube

49. chapter 3.4.1 | Applications: The Cube

50. ?chapter 3.4.1 | Applications: The CubeBut is it correct to just join the projected corners?

51. chapter 3.4.1 | Applications: The Straight Linex’ {m (ez- z1) – n (ey- y1)} – df m (ex - x1) = y’ {l (ez- z1) – n (ex - x1)} - df l (ey- y1).

52. chapter 3.4.1 | Applications: The Straight Line,

53. chapter 3.4.1 | Applications: The Straight Line(x’, y’) ≡ (x’, y’, df)= (x’ n/df, y’ n/df, n) = (l, m, n)

54. chapter 3.4.1 | Applications: The Straight Line

55. chapter 3.4.1 | Applications: The Straight Linel1l2+m1m2+n1n2 = l1l3+m1m3+n1n3 = l2l3+m2m3+n2n3 = 0.x1x2 + y1y2 = x1x3 + y1y3 = x2x3 + y2y3 = -df2.

56. chapter 3.4.1 | Applications: The Straight Linev1 (x1, y1)v2 (x2, y2)v3 (x3, y3)v1.v2 = v1.v3 ⇒ v1.(v2-v3) = 0.

57. chapter 3.4.1 | Applications: The Straight Linev1v2v3

58. chapter 3.4.2 | Applications: The Wallz = mx + d, y = ±h.

59. chapter 3.4.2 | Applications: The Walld = 2mh = 1.5mdf = 10cmθ = 60°

60. chapter 3.4.3 | Applications: The Staircase20 steps

61. chapter 3.4.3 | Applications: The Staircase10 steps above eye level7 steps below

62. chapter 3.4.3 | Applications: The StaircaseTill the 9th step below

63. chapter 3.4.3 | Applications: The StaircaseThe 10th step

64. chapter 3.4.3 | Applications: The Staircase

65. chapter 3.4.4 | Applications: The Circler = R, z= do

66. chapter 3.4.4 | Applications: The Circlex2 + y2 + (z-d)2 = r2, z = mx + d

67. chapter 3.4.4 | Applications: The Circle

68. chapter 3.4.4 | Applications: The Circle

69. chapter 3.4.5 | Applications: The Spherex2 + y2 + (z-d)2 = r2The perceived size of an object depends on the pairs of light rays emanating from it that subtend the greatest angle at the eye.

70. chapter 3.4.5 | Applications: The Sphere

71. chapter 3.4.5 | Applications: The Sphere

72. P’: (x’, y’)chapter 3.5 | Working Backwards: From Image to Object

73. chapter 3.5 | Working Backwards: From Image to Objectr’ = R

74. chapter 3.4.5 | Binocular Vision

75. ?chapter 3.4.5 | Binocular Vision(x, y, z) ≡ But does your brain know this formula?

76. chapter 3.4.5 | Binocular Vision

77. chapter 4 | The Circular and Spherical Scales

78. chapter 4 | The Circular and Spherical Scales

79. chapter 4.1 | Positionx’ =rfθ

80. chapter 4.1 | Position

81. chapter 4.2 | Applications: The Wallz = d, y = ±hBut this graph is WRONG!

82. chapter 4.2 | Applications: The Wall

83. chapter 4.2 | Applications: The Wall

84. chapter 5 | The Cylindrical Scale

85. chapter 5.1 | Position

86. chapter 5.2 | Applications: The Wallz = d, y = ±h

87. chapter 5.2 | Applications: The Wall

88. chapter 6| The Semicircular and Hemispherical Scales

89. chapter 6.1 | Position

90. chapter 6.2 | Applications: The Wallz = d, y = ±h

91. chapter 6.2 | Applications: The Wall

92. chapter 7| More on Binocular Vision

93. chapter 7 | More on Binocular Vision

94. chapter 7 | More on Binocular Vision

95. chapter 7 | More on Binocular Vision

96. chapter 7 | More on Binocular Vision

97. chapter 7 | More on Binocular Vision

98. chapter 7 | More on Binocular Vision

99. chapter 7 | More on Binocular Vision

100. Microsoft© Word TM and PowerPoint TMMathCastCopyright © 2004-2007 Tom Chakam www.mathcast.sf.netMathGVGraph www.padowan.dkMetaCreations Bryce 4Adobe© Photoshop TMCredits