Downloaded 21 times
Uploaded byArash Pourdamghani
A short introduction to Network coding
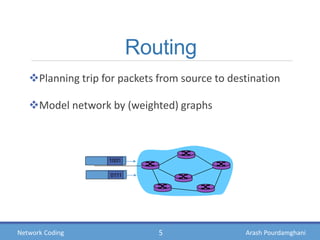
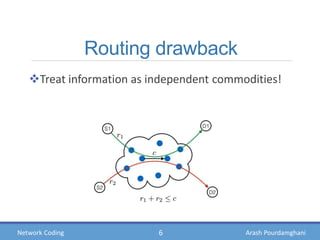
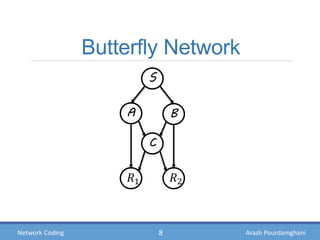
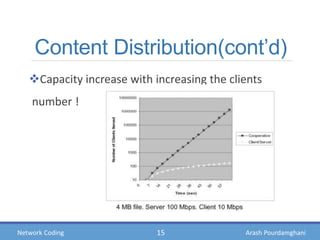
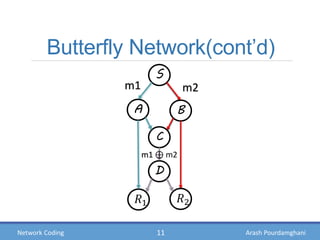
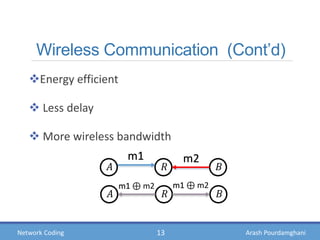
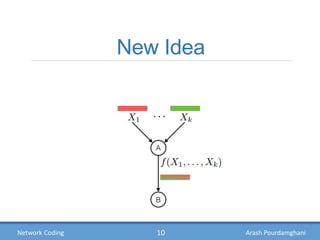
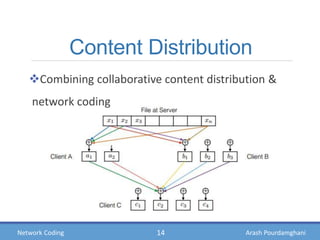
This document provides an introduction to network coding, including: - Examples of how network coding can increase throughput in butterfly networks and wireless communications - Theories showing how intermediate nodes can linearly combine information to deliver data at the maximum possible rate - Benefits of network coding like increased throughput and efficiency, but also challenges like integrating it into existing infrastructure
More Related Content
Similar to A short introduction to Network coding
A short introduction to Network coding
- 1. Network Coding Department ofComputer Engineering Sharif University of Technology Winter 2016 Arash Pourdamghani A Short Introduction to
- 2.
- 3.
- 4. Arash PourdamghaniNetwork Coding Networking Sharingresources Unify multiple devices Packet switching Through multiple layers 4
- 5. Arash PourdamghaniNetwork Coding Routing Planningtrip for packets from source to destination Model network by (weighted) graphs 0111 1001 5
- 6. Arash PourdamghaniNetwork Coding Routingdrawback Treat information as independent commodities! 6
- 7.
- 8. Arash PourdamghaniNetwork Coding ButterflyNetwork S A B C 𝑅1 𝑅2 8
- 9. Arash PourdamghaniNetwork Coding ButterflyNetwork(cont’d) S A B C 𝑅1 𝑅2 D S A B C 𝑅1 𝑅2 D S A B C 𝑅1 𝑅2 D 9
- 10.
- 11. Arash PourdamghaniNetwork Coding ButterflyNetwork(cont’d) S A B C 𝑅1 𝑅2 D m1 m2 m1 ⊕ m2 11
- 12. Arash PourdamghaniNetwork Coding WirelessCommunication A and B want to exchange 2 files by helping a relay node R (e.g. a satellite link) 𝐴 𝑅 𝐵 𝐴 𝑅 𝐵 𝐴 𝑅 𝐵 𝐴 𝑅 𝐵 m1 m1 m2 m2 12
- 13. Arash PourdamghaniNetwork Coding WirelessCommunication (Cont’d) Energy efficient Less delay More wireless bandwidth 𝐴 𝑅 𝐵 𝐴 𝑅 𝐵 m1 m2 m1 ⊕ m2 m1 ⊕ m2 13
- 14. Arash PourdamghaniNetwork Coding ContentDistribution Combining collaborative content distribution & network coding 14
- 15. Arash PourdamghaniNetwork Coding ContentDistribution(cont’d) Capacity increase with increasing the clients number ! 15
- 16.
- 17. Arash PourdamghaniNetwork Coding Otherdisciplines 17
- 18. Arash PourdamghaniNetwork Coding Overview 𝑆1,𝑆2, … 𝑆 𝑘 want to transmit to 𝑅1, 𝑅2, … 𝑅 𝑛 simulatencly 𝑆1 𝑆2 𝑆 𝑘 𝑅1 𝑅2 𝑅 𝑛 18 h
- 19. Arash PourdamghaniNetwork Coding Min-CutMax-Flow Acyclic graph G = (V,E) with unit capacity edges, a source vertex S, and a receiver vertex R. If the min-cut between S and R equals h, then the information can be send from S to R at a maximum rate of h. 19
- 20. Arash PourdamghaniNetwork Coding MainTheorem There exists a multicast transmission scheme over a large enough finite field 𝑭 𝒒, in which intermediate network nodes linearly combine their incoming information symbols over 𝐹𝑞, that delivers the information from the sources simultaneously to each receiver at a rate equal to h. 20
- 21. Arash PourdamghaniNetwork Coding MulticastTransmission One-to-many communication with specific receiver addresses 21
- 22. Arash PourdamghaniNetwork Coding FiniteFields Abelian Group -> Galois Field -> Extension Fields Closure, Associativity, Commutativity Identity & Inverse element Closed on ‘+’ and ‘.’ 22 + 0 1 0 0 1 1 1 0 . 0 1 0 0 0 1 0 1
- 23. Arash PourdamghaniNetwork Coding FiniteFields(cont’d) Prime Fields: 𝐺𝐹(𝑝) where 𝑝 is prime number Extension fields: 𝐺𝐹(𝑝 𝑚) where 𝑝 is prime number and 𝑚 > 1 23 + 0 1 A B 0 0 1 A B 1 1 0 B A A A B 0 1 B B A 1 0 . 0 1 A B 0 0 0 0 0 1 0 1 A B A 0 A B 1 B 0 B 1 A
- 24. Arash PourdamghaniNetwork Coding Proofmethods •Algebraic • There exist values in some large enough finite field 𝐹𝑞 for the components {𝛼 𝑘} of the local coding vectors, such that all matrices 𝑨𝒋,1 ≤ j ≤ N, defining the information that the receivers observe, are full rank . •Information Theoretic • For each vertex 𝑣 select |𝑂𝑢𝑡(𝑣)| functions 𝑓𝑖 𝑣 : 2ℎ 𝐼𝑛 𝑣 → 2ℎ chosen uniformly at random • Each receiver could decode all source packets if get sufficient input packets 24
- 25.
- 26. Arash PourdamghaniNetwork Coding Benefits Throughputincrement In place coding Efficiency of wireless resources Using current cables 26
- 27. Arash PourdamghaniNetwork Coding27 Coding Advantage DIRECTED GRAPHS Multicast : Ω( 𝑛) Multiple unicast: Ω(𝑛) UNDIRECTED GRAPHS Upper bound is 2 Lower bound is 8 7 27
- 28. Arash PourdamghaniNetwork Coding Challenges Dynamicchanges Complexity of computations Security of transmitted data Integration with existing infrastructure 28
- 29. Arash PourdamghaniNetwork Coding References J.Kurose, K. Ross, “Computer Networking: Top- Down Approach”,6th edition, Addison Wesley, 2013 M. Jafari Siavoshani, ”A Very Short Introduction to Network Coding”, Sharif University of Technology, Fall 2014 29
- 30. Arash PourdamghaniNetwork Coding References(cont’d) C.Fragouli, E. Soljanin, “Network coding fundamentals” Foundations and Trends in Networking, 2007 A. Sprintson, Theory and application of network coding, Texas A&M University, 2016 30
- 31.