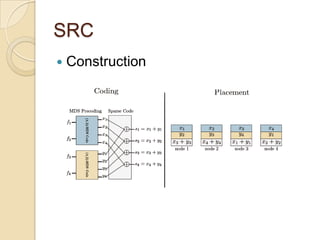
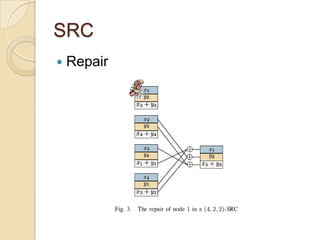
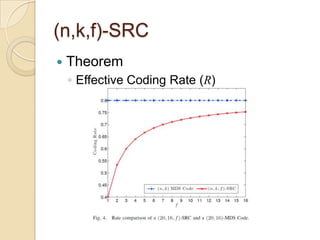
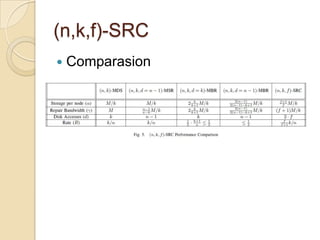
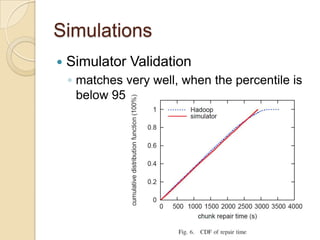
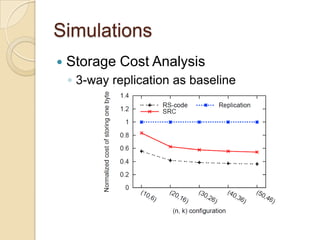
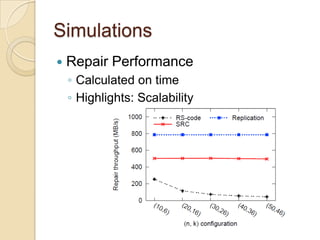
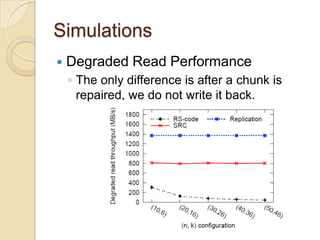
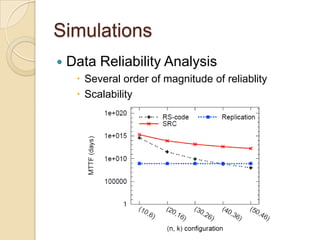
The document presents Simple Regenerating Codes (SRC) for efficient data repair in cloud storage systems. SRC combines MDS codes for reliability with XOR operations to allow repair using minimal bandwidth and disk I/O. Simulations show SRC reduces storage costs compared to replication and maintains high reliability while improving repair scalability through reduced repair bandwidth and disk accesses.

1. Simple Regenerating Codes:
Network Coding for Cloud
Storage
Dimitris S. Papailiopoulos, Jianqiang Luo,
Alexandros G. Dimakis, Cheng Huang, and Jin Li
INFOCOM 2012
Presented by Tangkai

2. Index
 About the author
 Introduction
 SRC
 Simulations
 Conclusion

3. About the author
 Jianqiang Luo
◦ Experience
 Senior Software Engineer @ EMC
 Received PhD, Wayne State University
 Intern @ Microsoft, Data Domain
 Team Leader @ Actuate
 Received MS, SJTU
◦ Specialties
 Working on distributed storage systems during
PhD
Performance profiling.

4. About the author
 Alexandros G. Dimakis
◦ Assistant Professor
Dept of EE – Systems, USC
◦ Research interests:
 Communications, signal processing and
networking.
◦ INFOCOM 2012 - 2
◦ Erasure code MDS MSR MBR etc

5. About the author
 Cheng Huang
◦ Education
 Microsoft Research
 Ph.D. Washington University
 B.S. and M.S. EE Dept, SJTU
◦ Research interest
 cloud services, internet measurements, erasure
correction codes, distributed storage systems, peer-to-
peer streaming, networking and multimedia
communications.
◦ INFOCOM 2011
 Public DNS System and Global Traffic Management
 Estimating the Performance of Hypothetical Cloud
Service Deployments: A Measurement-Based Approach

6. About the author
 Jin Li
◦ Experience
 Microsoft Research
 BS/MS/PhD THU (within 7 years)
 计算机普及要从娃娃抓起
◦ Title
 IEEE Fellow
 GLOBECOM/ICME/ACM MM Chair

7. Index
 About the author
 Introduction
 SRC
 Simulations
 Conclusion

8. Introduction
 Background
◦ We have come into BIG DATA ERA!
 Digital Universe 1.8 ZB (=1.8e9 TB)
 Several PBs photo stored on Facebook
 14.1PB data stored on Taobao (2010)
◦ Data security is IMPORTANT
 Free from unwanted actions of unauthorized
users.
 Free from data loss caused by destructive
forces

9. Introduction
 Background
◦ Recovery
 rare exception -> regular operation
 GFS[1]:
 Hundreds or even thousands of machines
 Inexpensive commodity parts
 High concurrency/IO
◦ High failure tolerance, both for
 High availability and to prevent data loss
[1] S. Ghemawat, H. Gobioff, and S.-T. Leung, “The Google file system,” in
SOSP ’03: Proc. of the 19th ACM Symposium on Operating Systems
Principles, 2003.

10. Introduction
 Background
◦ Erasure coding > replication
 1. redundancy level, reliability
 2. reliability, storage cost
◦ Some applications
 Cloud storage systems
 Archival storage
 Peer-to-peer storage systems

11. Introduction
 Erasure coding: MDS n=3 n=4
k=2
File or A A
data A
object
A B B B
B
A+B A+B
(3,2) MDS code,
(single parity) A+2B
used in RAID 5
(4,2) MDS
code. Tolerates
any 2 failures
Used in RAID 6

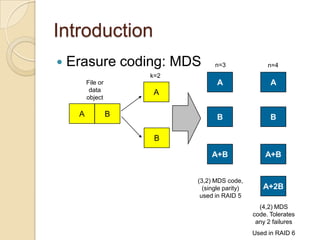
12. Introduction
 Erasure coding vs. Replica[3]erasure code
(4,2) MDS
Replication (any 2 suffice to recover)
File or A A
data A
object
A B
vs
B
B A+B
B A+2B
[3]A. G. Dimakis, P. G. Godfrey, Y. Wu, M. J. Wainwright, and K. Ramchandran,“Network
coding for distributed storage systems,” in IEEE Trans. on Inform. Theory, vol. 56, pp.

13. Introduction
 Erasure coding vs. Replica[3]erasure code
(4,2) MDS
Replication (any 2 suffice to recover)
File or A A
data A
object
A B
Erasure coding is introducing redundancy in an optimal way.
vs
B Very useful in practice
i.e. Reed-Solomon codes, Fountain Codes, (LT and Raptor)…
B A+B
B A+2B
[3]A. G. Dimakis, P. G. Godfrey, Y. Wu, M. J. Wainwright, and K. Ramchandran,“Network
coding for distributed storage systems,” in IEEE Trans. on Inform. Theory, vol. 56, pp.

14. Introduction
 Metrics
◦ Storage per node (α)
◦ Repair Bandwidth per single node repair
(γ)
◦ Disk Accesses per single node repair (d)
◦ Effective Coding Rate (R)
 Contribution
◦ High R, Small d
◦ Low repair computation complexity

15. Index
 About the author
 Introduction
 SRC
 Simulations
 Conclusion

16. SRC
 SRC: Simple Regenerating Codes
◦ Regenerating Codes
 address the issue of rebuilding (also called
repairing) lost encoded fragments from existing
encoded fragments. This issue arises in
distributed storage systems where
communication to maintain encoded
redundancy is a problem.

17. SRC
 Object
 Requirement I: (n, k) property
 MDS[2]
[2] Alexandros G. Dimakis, Kannan Ramchandran, Yunnan
Wu, Changho Suh:
A Survey on Network Codes for Distributed Storage. in Proceedings of the

18. SRC
◦ MDS

19. SRC
 Requirement II: efficient exact repair
◦ Efficient: Low complexity
◦ Exact repair (vs. functional repair)[3] :
 1. [demands]Data have to stay in systematic
form
 2. [complexity]Updating repairing-decoding
rules-> additional overhead
 3. [security] dynamic repairing-and-decoding
rules observed by eavesdroppers ->
information leakage
[2] Changho Suh, Kannan Ramchandran: Exact Regeneration Codes
for Distributed Storage Repair Using Interference Alignment. in IEEE
TRANSACTIONS ON INFORMATION THEORY, VOL. 57, NO. 3, MARCH

20. SRC
 Solution
◦ MDS codes are used to provide reliability
to meets Requirement I
◦ simple XORs applied over the MDS coded
packets provide efficient exact repair to
meets Requirement II

21. SRC
 Construction

22. SRC
 Repair

23. (n,k,2)-SRC
 Code Construction
◦ File f , of size M = 2k
◦ Split into 2 parts
◦ 1. 2 independent (n,k)-MDS encoding
◦ 2. Generating a parity sum vector using
XOR

24. (n,k,2)-SRC
 Distribution
◦ 3n chunks in n storage nodes

25. (n,k,2)-SRC
 Repair

26. (n,k,f)-SRC
 General Code Construction
◦ File f , of size M = fk
◦ Cut into f parts
◦ 1. f independent (n,k)-MDS encoding
◦ 2. Generating a parity sum vector using
XOR

27. (n,k,f)-SRC
 Distribution
◦ (f+1)n chunks in n storage nodes

28. (n,k,f)-SRC
 Repair

29. (n,k,f)-SRC
 Theorem
◦ Effective Coding Rate (R)
 SRC is a fraction f/f+1 of the coding rate of an
(n, k) MDS code, hence is upper bounded

30. (n,k,f)-SRC
 Theorem
◦ Effective Coding Rate (R)

31. (n,k,f)-SRC
 Theorem
◦ Storage per node (α)
◦ Repair Bandwidth per single node repair
(γ)
◦ Disk Accesses per single node repair (d)
 Seek time

32. (n,k,f)-SRC
 Theorem
◦ Disk Accesses per single node repair (d)
 Starting with f disk accesses for the first chunk
repair

33. (n,k,f)-SRC
 Theorem
◦ Disk Accesses per single node repair (d)
 each additional chunk repair requires an
additional disk access

34. (n,k,f)-SRC
 Comparasion

35. (n,k,f)-SRC
 Asymptotics of the SRC -> MDS
◦ let the degree of parities f grow as a
function of k
◦ Repair Bandwidth per single node repair
(γ)
◦ Effective Coding Rate (R)

36. Index
 About the author
 Introduction
 SRC
 Simulations
 Conclusion

37. Simulations
 Simulator Introduction
◦ One master, other storage server.
◦ Chunks form the smallest accessible data
units and in our system are set to be
64MB
 Simulator Validation
◦ 16 machines
◦ 1Gbps network.
◦ 410GB data per machine
◦ Approximately 6400 chunks

38. Simulations
 Simulator Validation
◦ matches very well, when the percentile is
below 95

39. Simulations
 Storage Cost Analysis
◦ 3-way replication as baseline

40. Simulations
 Repair Performance
◦ Calculated on time
◦ Highlights: Scalability

41. Simulations
 Degraded Read Performance
◦ The only difference is after a chunk is
repaired, we do not write it back.

42. Simulations
 Data Reliability Analysis
◦ simple Markov model to estimate the
reliability
◦ 5 years /1PB data /
◦ 30 min for replica / 15 min for SRC

43. Simulations
 Data Reliability Analysis
 Several order of magnitude of reliablity
 Scalability

44. Index
 About the author
 Introduction
 SRC
 Simulations
 Conclusion

45. Conclusions
 Highlight
◦ R-S
 Low IO/bandwidth -> scalability
◦ replica
 High reliability
 Decent repair/degraded read performance

46. Critical Thinking
 Simulation
 （n, k）as n grows, erasure
performance is weaker
 Compare
◦ MSR?
◦ Exact?
◦ Implementation - > Simulation