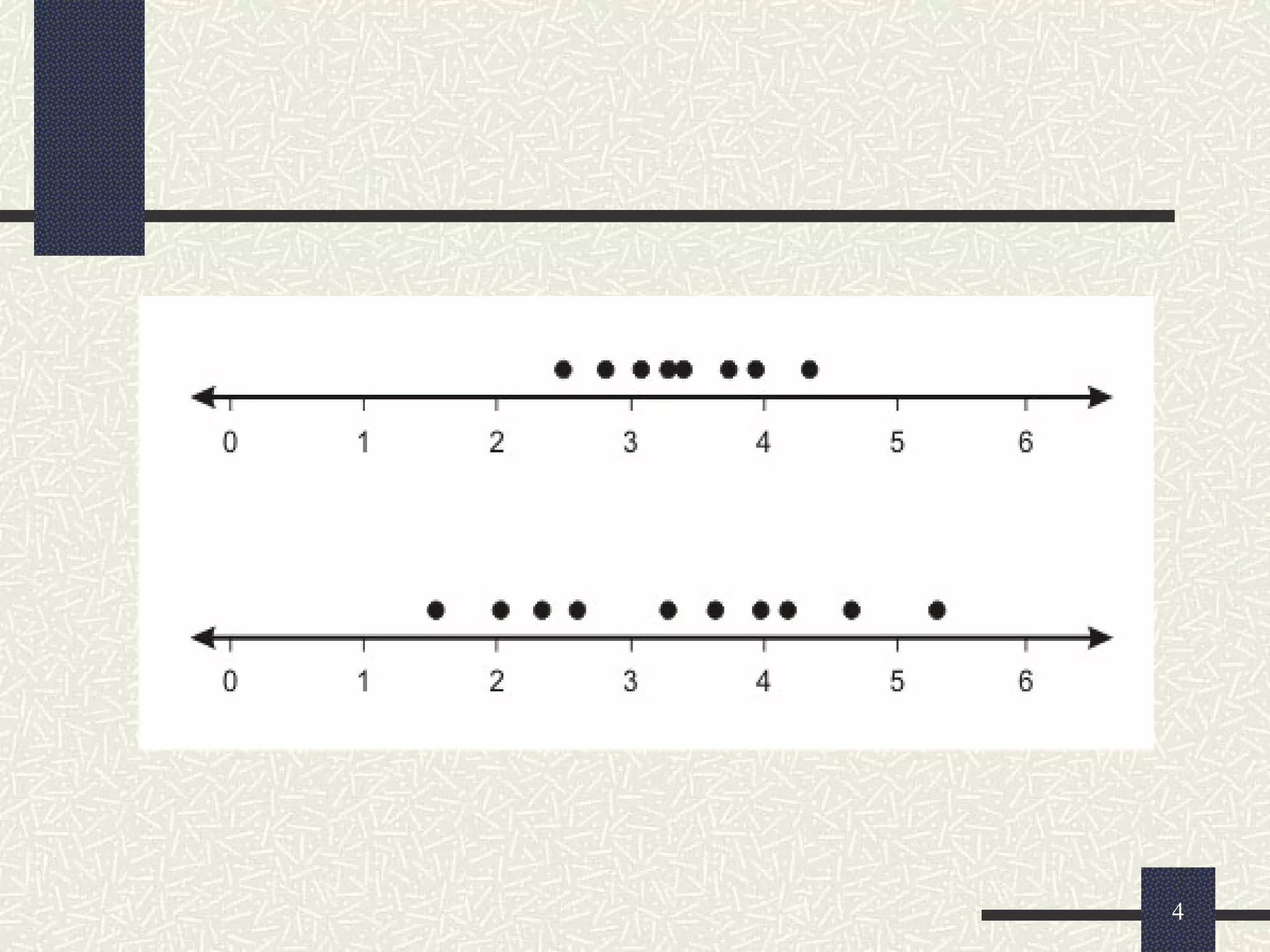
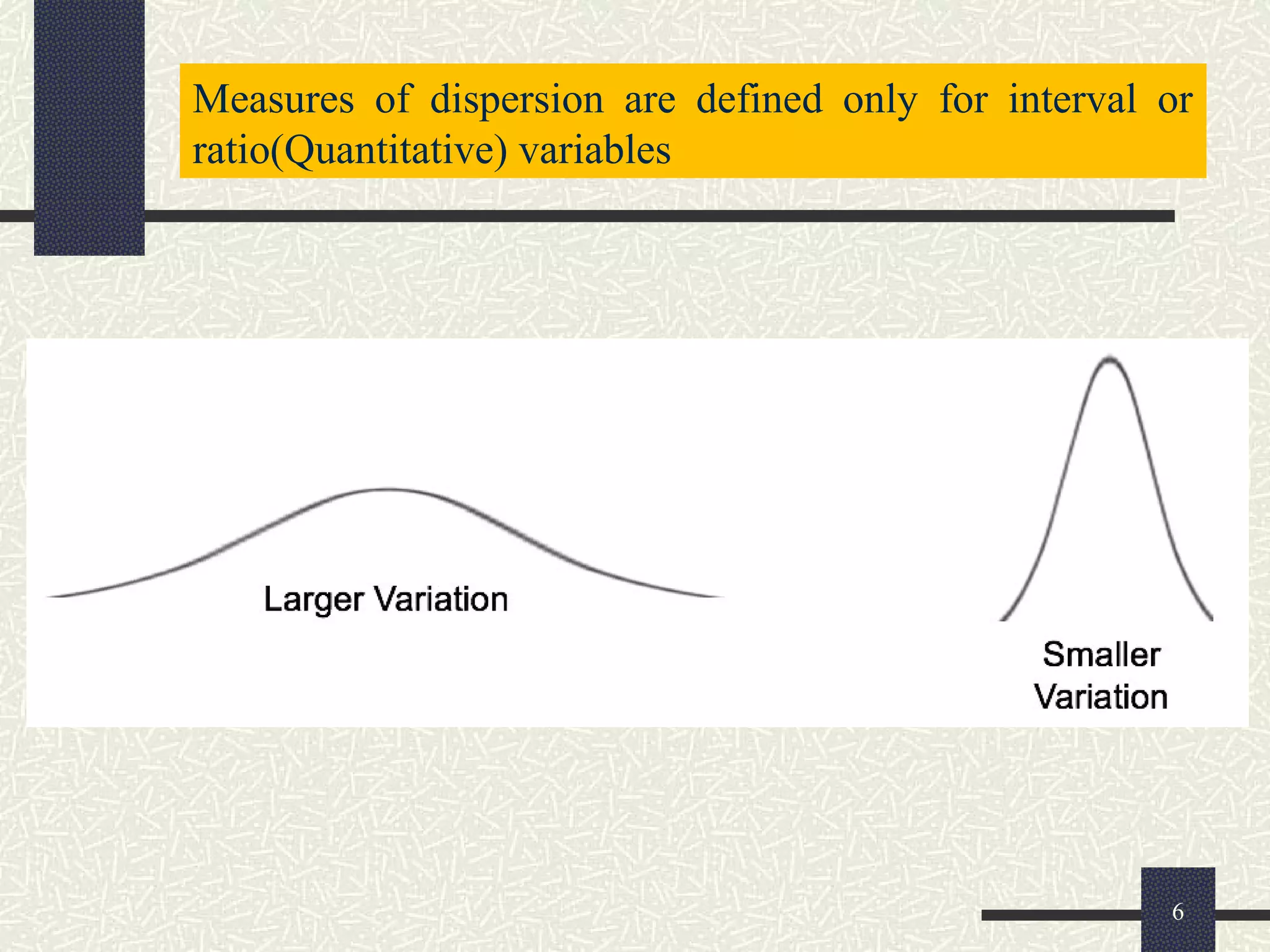
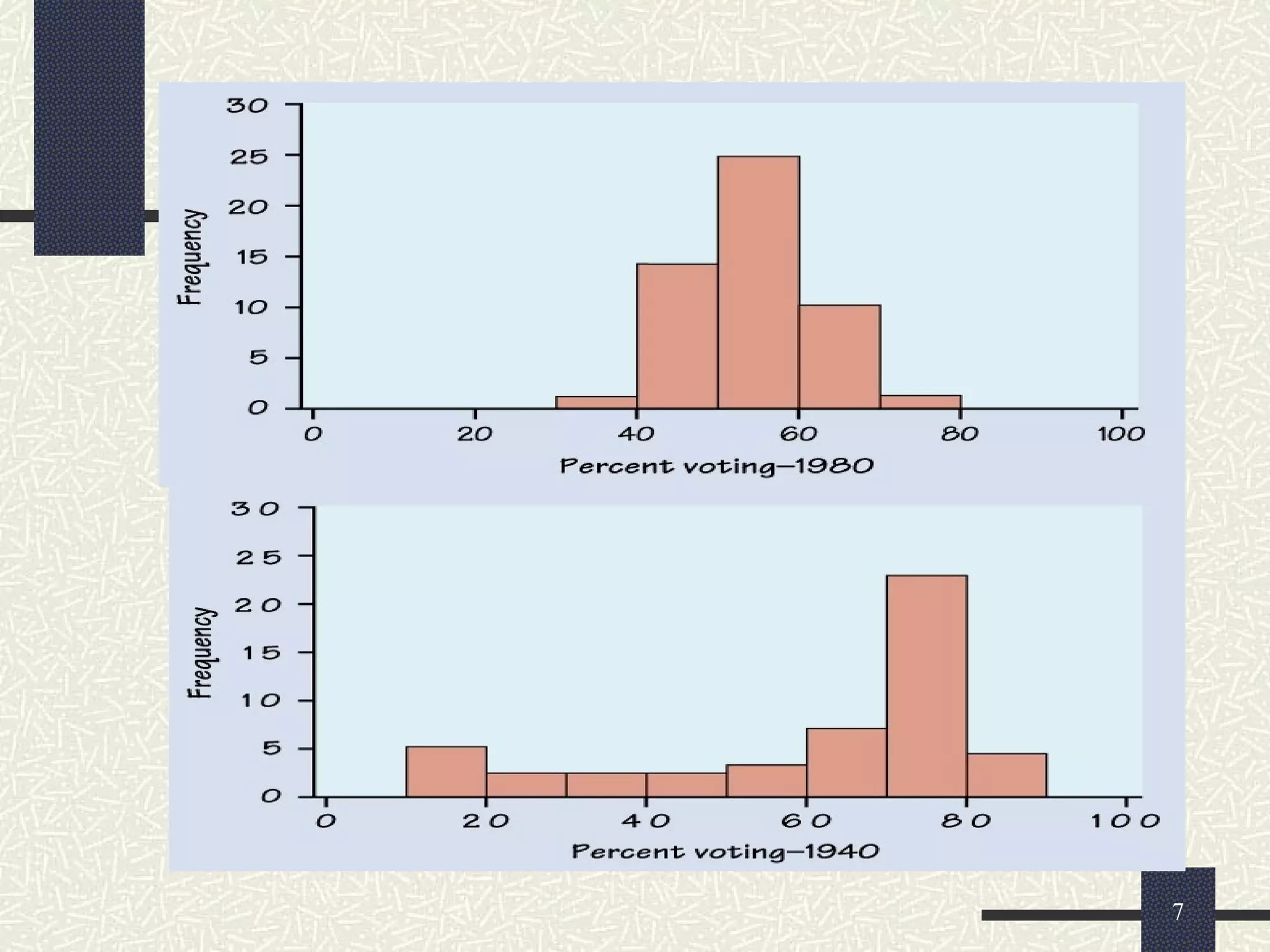
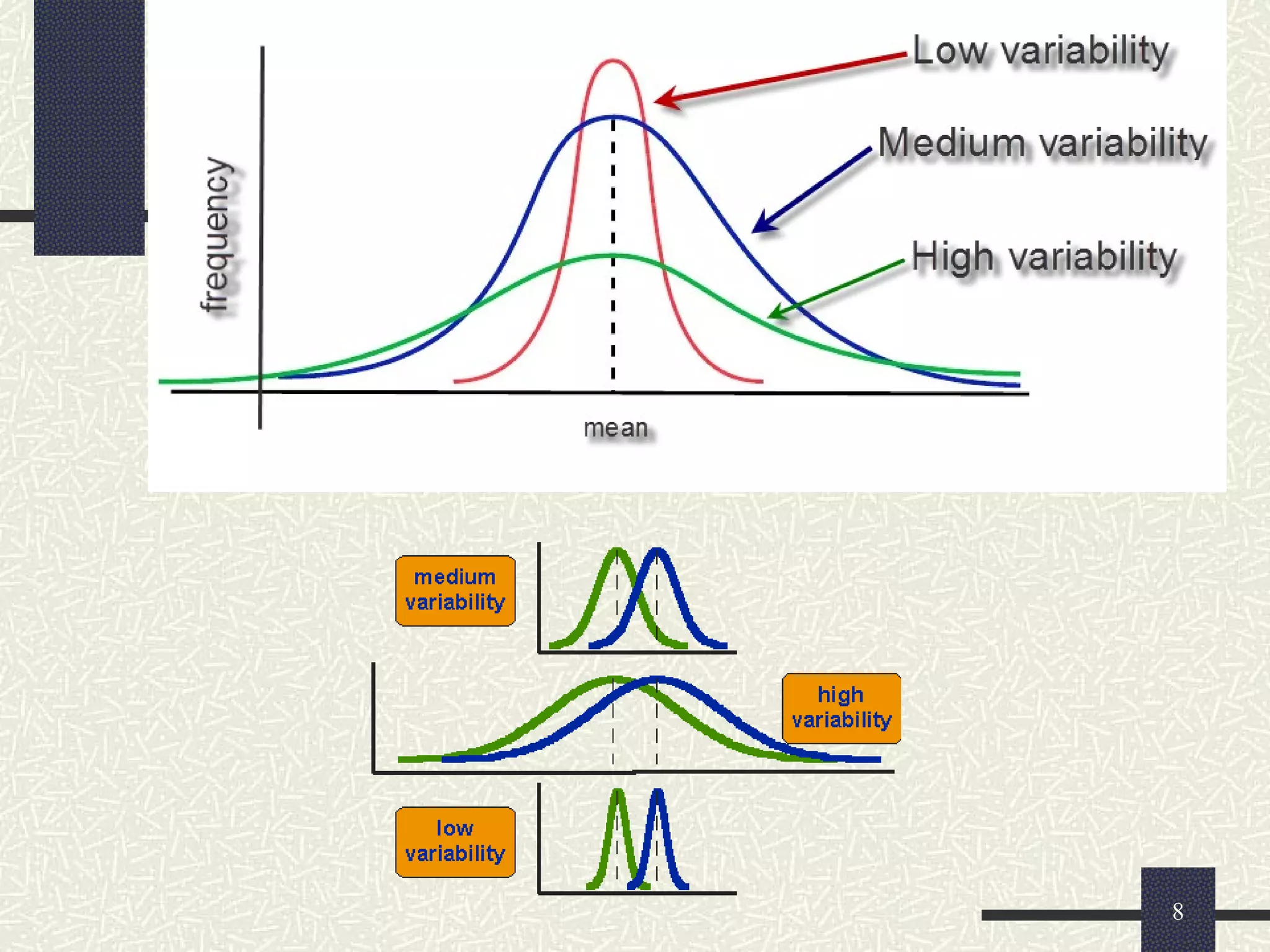
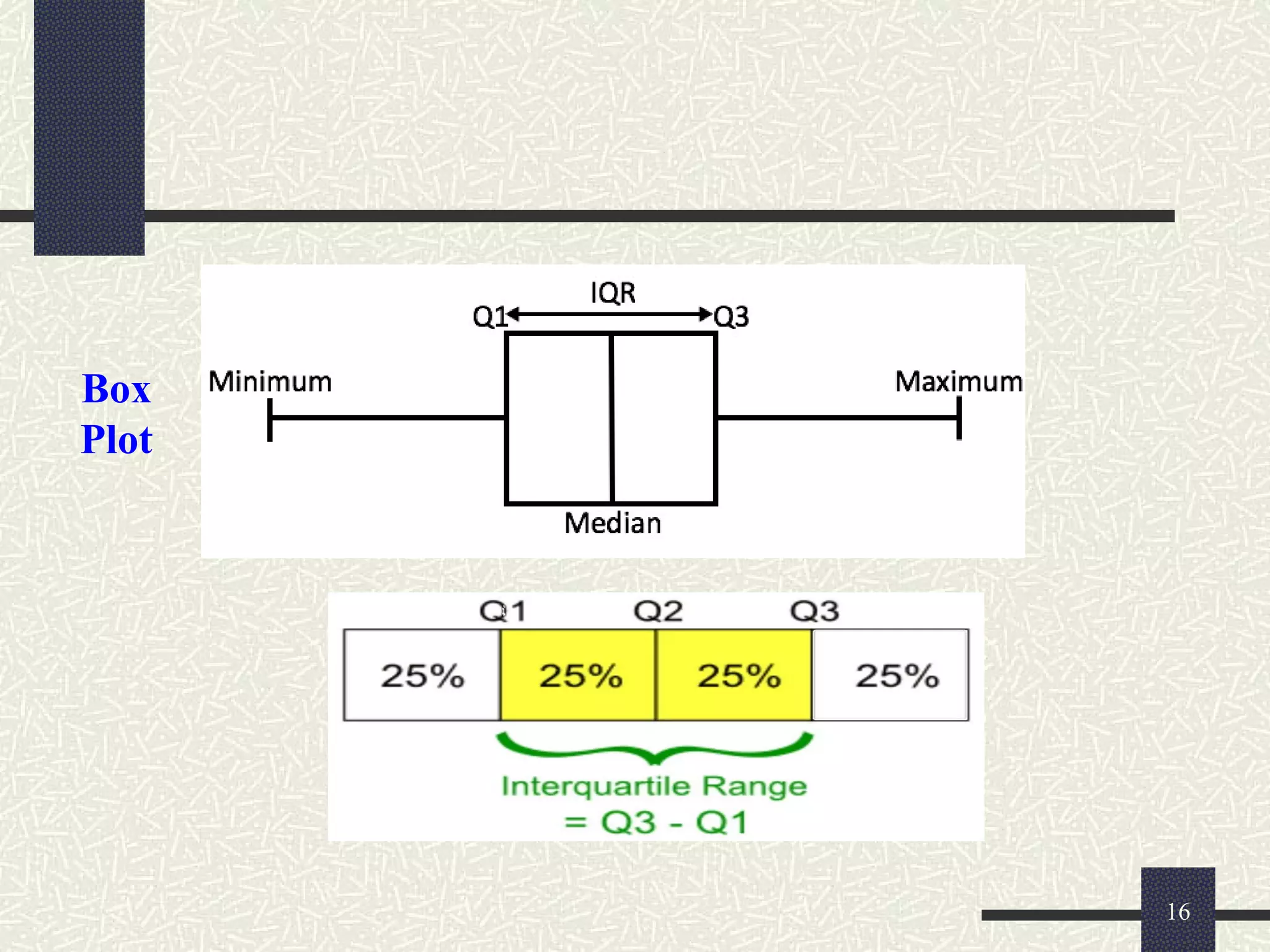
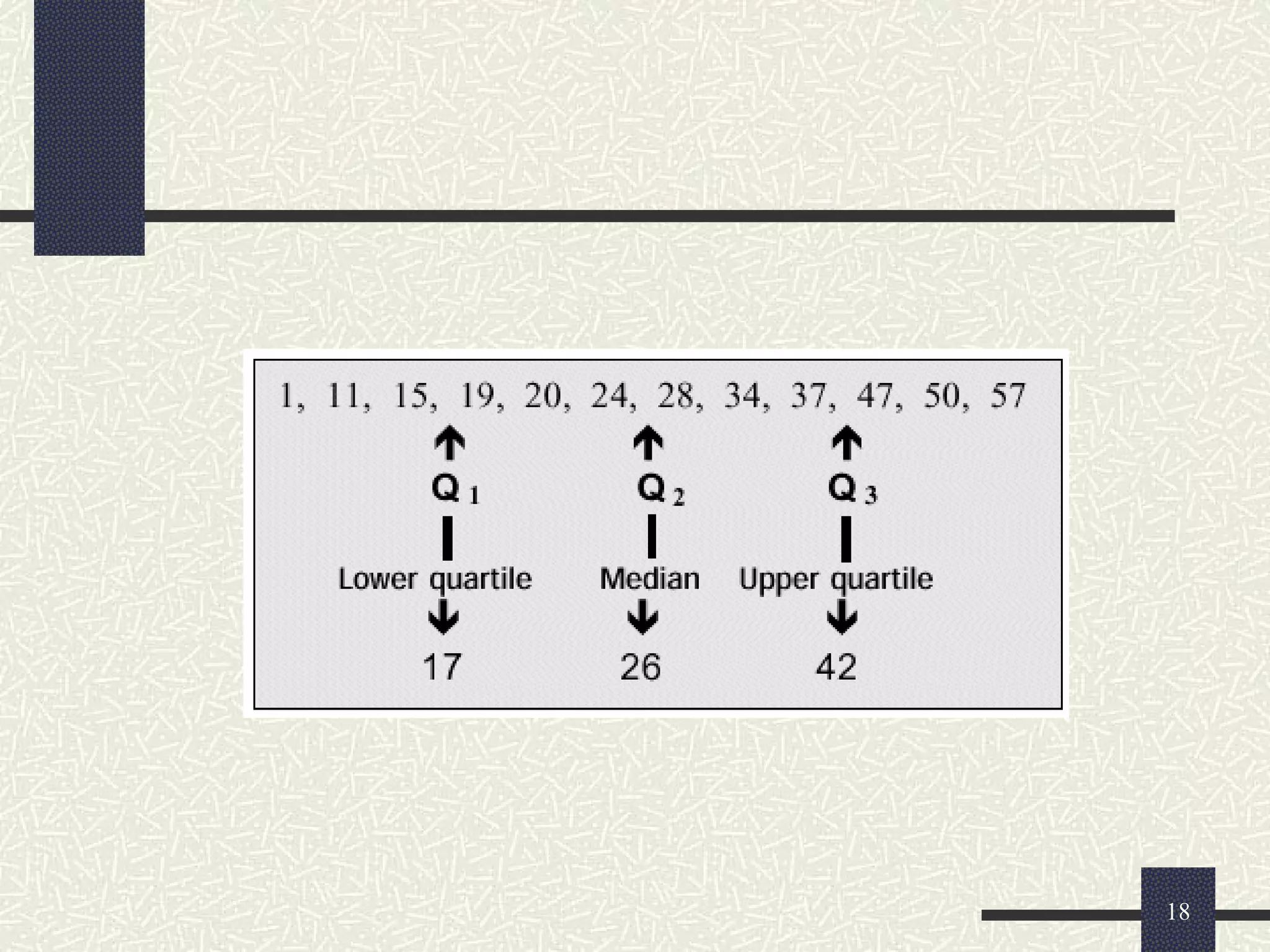
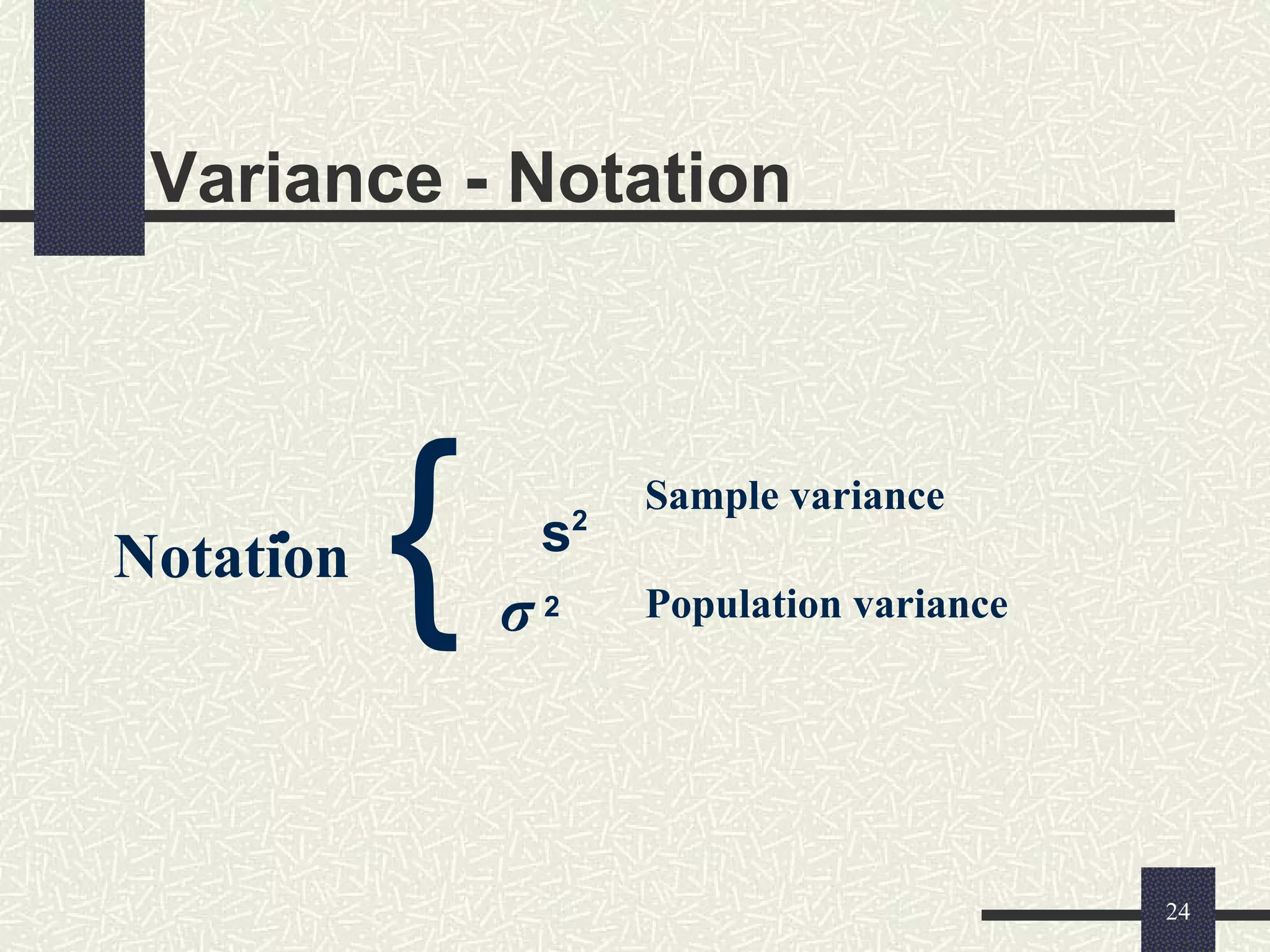
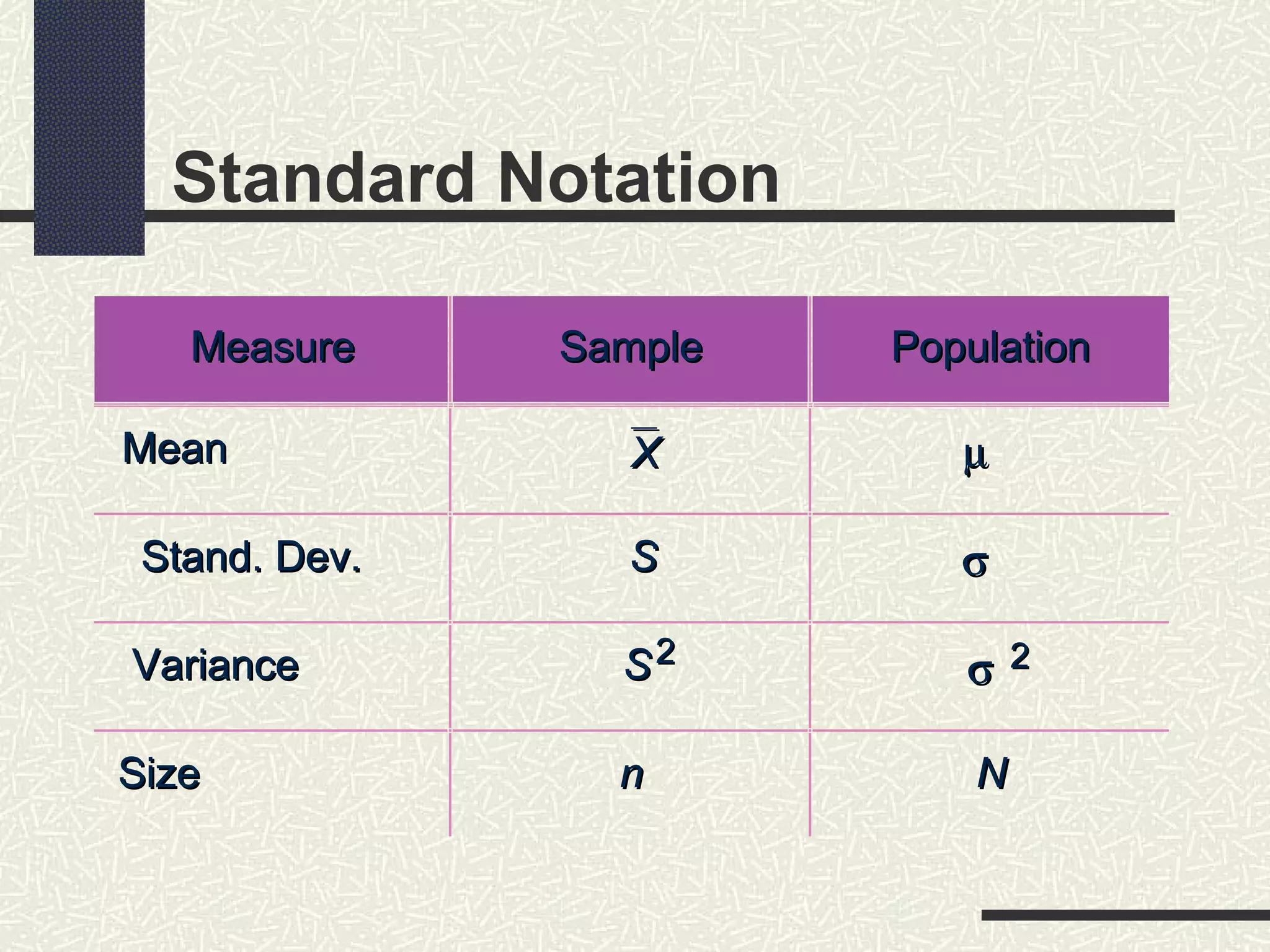
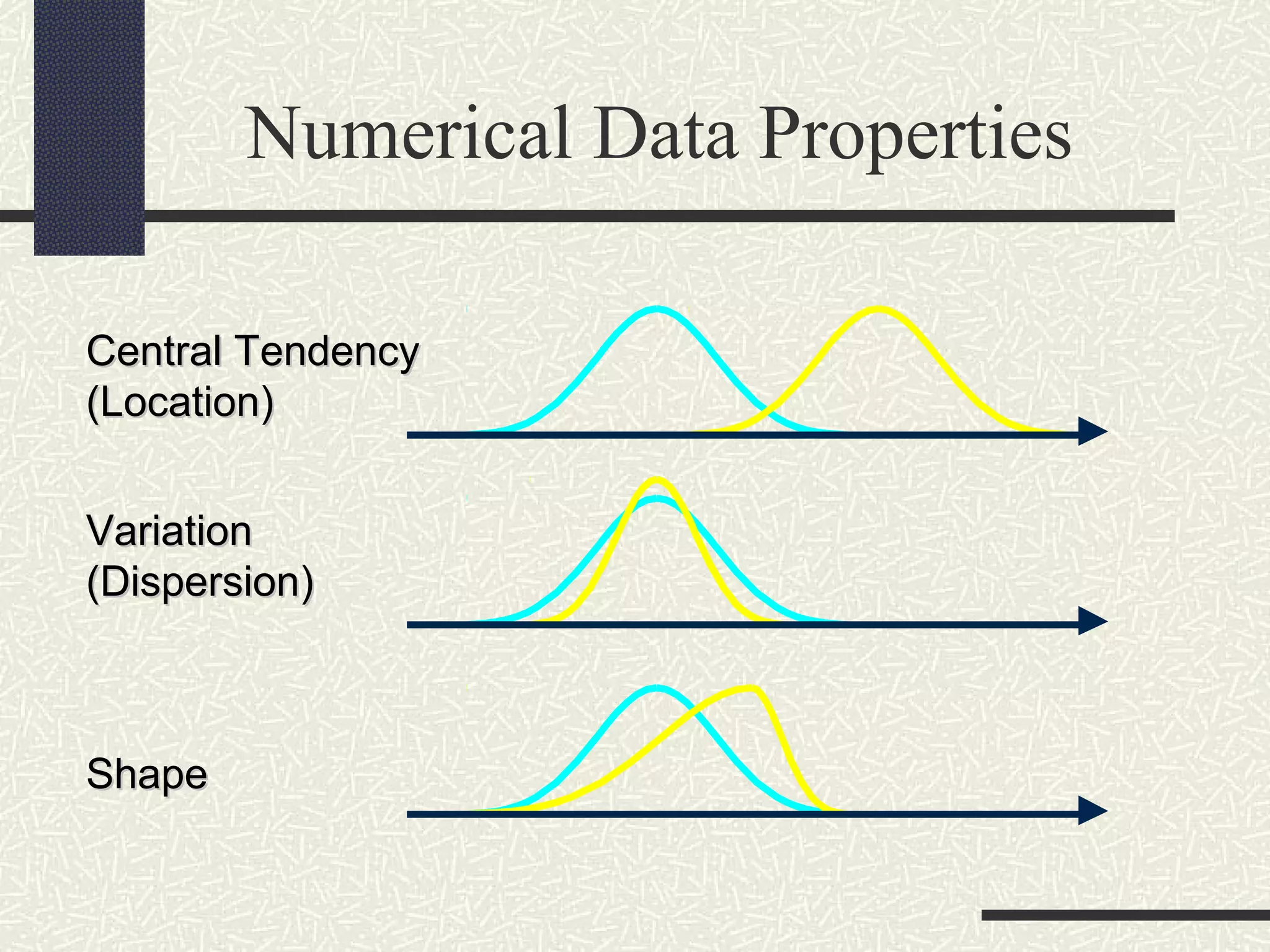
The document discusses measures of dispersion in statistics, which quantify variability in data sets. It outlines different types of dispersion measures, including range, interquartile range, variance, standard deviation, and coefficient of variation. Additionally, it explains how these measures help in understanding the spread of data points around the mean.

1. Measures of Dispersion/Variation/Spread
Dr. Athar KhanDr. Athar Khan
Associate ProfessorAssociate Professor
Department of Community MedicineDepartment of Community Medicine
Liaquat College of Medicine & DentistryLiaquat College of Medicine & Dentistry

2. Measures of Variation/Dispersion
2

3. Group A
10,20,30,40,50,60,70
MEAN = ?
Group B
25,30,40,40,45,50,50
MEAN = ?
3

4. 4

5. Measure of Dispersion/Variability/Spread
• A measure of dispersion conveys information regarding the amount
of variability (heterogeneity) present in a set of data.
• OR
• In statistics, a measure of how much the data in a certain collection
are scattered around the mean.
• OR
• Measures of dispersion (or variability or spread) indicate the extent
to which the observed values are “spread out” around that
center OR how “far apart” observed values typically are from
each other and from some average(mean) ------ JSMU
5

6. 6
Measures of dispersion are defined only for interval or
ratio(Quantitative) variables

7. 7

8. 8

9. Measure of Dispersion
There are two principal types of measures of
dispersion: RANGE measures and DEVIATION
measures.
Range measures are based on the distance between
pairs of (relatively) “extreme” values observed in the
data (MAXIMUM – MINIMUM).
Deviation measures are based on average deviations
from some average value.
9

10. Measure of Dispersion
• A measure of dispersion conveys information regarding the amount
of variability (heterogeneity) present in a set of data.
1. Range (R)
2. Inter Quartile Range (IQR)
3. Variance
4. Standard Deviation
5. Coefficient of variation (C.V)
 If all values different - Dispersion.
 If all values same No dispersion.
If values close to each other - Smaller
Dispersion.
 If values widely scattered - Greater
Dispersion. 10

11. Measures of Variation
11
• Range
•Variance
•Standard Deviation
•Mean or Average Deviation
•Coefficient of Variation

12. Range
 The difference in value between the
highest (maximum) and lowest
(minimum) observation
 Range =
 Quick measure of variability
 Greatly affected by extreme values
 Range is zero if all the values in a data set
are equal.
12
minmax xx −

13. Examples of Range
Distribution 1
32,35,36,36,37,38,40,42,42,43,43,45
Distribution 2
22,32,33,33,33,34,34,34,34,34,35,65
13

14. Inter Quartile Range (IQR)
• Distance between 1st
& 3rd
quartiles IQR
= Q3 - Q1
• Provides information about how much distance
is covered by middle 50% of the distribution.
14

15. INTERQUARTILE RANGE
The interquartile range is the value of the case that
stands at the 75th
percentile of the distribution
minus the value of the case that stands at the 25th
percentile (Q3 – Q1).
75th
percentile (Q3) - 25th
percentile (Q1)
15

16. 16
Box
Plot

17. 17

18. 18

19. Interdecile Range
The interdecile range is the value of the case
that stands at the 90th
percentile of the
distribution minus the value of the case that
stands at the 10th
percentile.
90th
percentile - 10th
percentile
19

20. Margin of Error
 Margin of error specifies the range between the
value of the sample statistic that stands at the
97.5th percentile minus the sample statistic that
stands at the 2.5th
percentile.
 97.5th
percentile – 2.5th
percentile
20

21. 21
Method
X X
X – X (X – X)2
Σ x =
X =Σ x /n Σ X - X= Σ (X – X)2 =
xxxxx

22. Mean Deviation
Defined as “average of the deviations from
the mean.”
M.D = Σ(x – x) (Ignoring+sign)
n
22

23. Variance
Defined as “squared difference of each
value from mean.” OR “the average of the
squared deviations from the mean”
s2
= Σ(x – x)2 SAMPLEVARIANCE
n-1 (n-1 is Degree of Freedom)
s2
= Σ(x – x)2 SAMPLEVARIANCE(Ifsample
n size is more than 30)
23

24. Variance - Notation
 s2
2
}Notation
Sample variance
Population variance
24
σ

25. Standard Deviation
•The standard deviation of a set of sample
values is a measure of variation of values
about the mean
•The square root of the variance is called the
standard deviation. ---- JSMU
• The SD is never less than the MD; the SD is
somewhat larger than the MD — typically
about 20-50%
25

26. Standard Deviation
 The value of the standard deviation is +
26
• Population standard deviation “σ” (sigma).
•Sample standard deviation “s”
• Sometimes written as SD

27. 27
Sample Population
Mean =Σ x /n µ =Σ x /N
Variance s2
= Σ(x – x )2
n-1
σ 2
= Σ(x –µ )2
N
Standard Deviation s = √ s2
σ = √ σ2
xx

28. Coefficient of Variation
 Ratio measure of dispersion/inequality is called
the coefficient of variation, which is simply
the standard deviation divided by the mean.
 CV = SD/Mean
 The lower the CV, the greater the reliability of a
variable
•100%
s
xCV =
Sample
28

29. Gini Index
Another measure of dispersion in ratio variables
is the Gini Index of Inequality. Gini Index is also
standardized, with values that range from a
minimum of 0 (perfect equality) to a maximum of
1 (perfect inequality).
29

30. Standard Notation
MeasureMeasure SampleSample PopulationPopulation
MeanMean XX µµ
Stand. Dev.Stand. Dev. SS σσ
VarianceVariance SS 22
σσ 22
SizeSize nn NN

31. Numerical Data Properties
Central TendencyCentral Tendency
(Location)(Location)
VariationVariation
(Dispersion)(Dispersion)
ShapeShape

32. THANKS