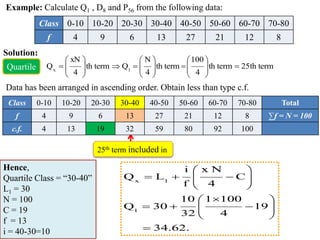
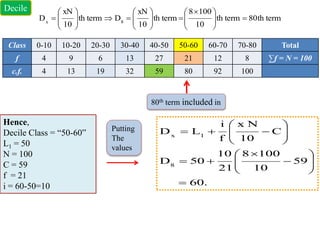
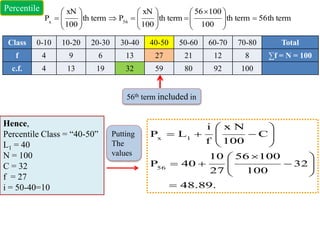
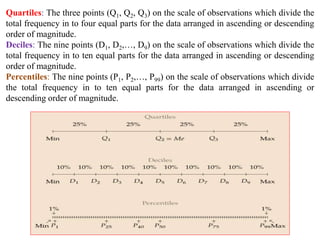
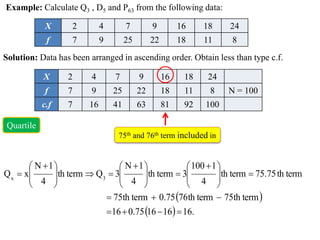
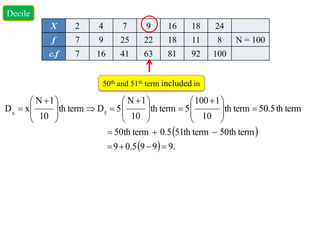
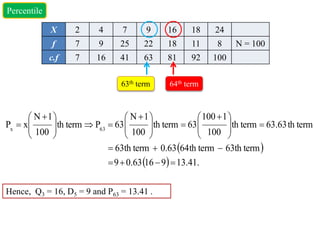
This document provides information about calculating quartiles, deciles, and percentiles from grouped and ungrouped data. It defines quartiles, deciles, and percentiles as points that divide the total frequency of data into four, ten, and one hundred equal parts, respectively. Formulas are provided to calculate the first, second, third, etc. quartile, decile, and percentile values based on the cumulative frequency of data arranged in ascending or descending order. An example calculation is shown for finding the first quartile, eighth decile, and 56th percentile from a grouped frequency distribution.

1. Title of the Course: Statistical Methods
Class: Second Year, First Semester
Teacher:
Dr. Ramkrishna Singh Solanki
Assistant Professor: Mathematics and Statistics
Contact: +919826026464
email: rsolankisolanki_stat@jnkvv.org
College of Agriculture Balaghat
Murjhad Farm, Waraseoni, M.P. 481331

2. “Quartiles, Deciles, Percentiles”
Partition Values

3. Quartiles: The three points (Q1, Q2, Q3) on the scale of observations which divide the
total frequency in to four equal parts for the data arranged in ascending or descending
order of magnitude.
Deciles: The nine points (D1, D2,…, D9) on the scale of observations which divide the
total frequency in to ten equal parts for the data arranged in ascending or descending
order of magnitude.
Percentiles: The nine points (P1, P2,…, P99) on the scale of observations which divide
the total frequency in to ten equal parts for the data arranged in ascending or
descending order of magnitude.

4. PARTITIONS VALUES FOR Raw Data: UNGROUPED DATA
term
or
value
th
4
1
N
x
Q
Quartitile x 






 


In the case of Ungrouped Data arranged the data in ascending order and let N be the
number of observation then partitions values is given by:
Where, x = 1, 2, 3
term
or
value
th
10
1
N
x
D
Decile x 






 


Where, x = 1, 2,…, 9
term
or
value
th
100
1
N
x
P
Percentile x 






 


Where, x = 1, 2,…, 99

5. Example: Calculate Q2 , D7 and P36 from the following data:
33, 22, 55, 47, 21, 68, 49, 40, 33, 70, 38, 42, 48, 52, 37.
Solution: Arrange the data in ascending order:
X: 21, 22, 33, 33, 37, 38, 40, 42, 47, 48, 49, 52, 55, 68, 70 Hence, N = 15
42
term
th
8
term
th
4
1
15
2
term
th
4
1
N
2
Q
term
th
4
1
N
x
Q 2
x









 








 









 

 
  .
60
.
49
49
52
20
.
0
49
term
th
11
term
th
12
20
.
0
term
th
11
term
th
20
.
11
term
th
10
1
15
7
term
th
10
1
N
7
D
term
th
10
1
N
x
D 7
x















 








 









 

 
  .
76
.
37
37
38
76
.
0
37
term
th
5
term
th
6
76
.
0
term
th
5
term
th
76
.
5
term
th
100
1
15
36
term
th
100
1
N
36
P
term
th
100
1
N
x
P 36
x















 








 









 

Hence, Q2 = 42, D7 = 49.60 and P36 = 37.76.
Quartile
Decile
Percentile

6. PARTITIONS VALUES FOR GROUPED DATA: Discrete frequency distribution
term
or
value
th
4
1
N
x
Q
Quartitile x 






 


In the case of Discrete frequency distribution the computation of partitions values
involves the following steps:
1. arranged the data in ascending order of magnitude (if not arranged).
2. Find the less than type cumulative frequencies (c.f.).
3. Calculate the partitions values using following formulae.
Where, x = 1, 2, 3
term
or
value
th
10
1
N
x
D
Decile x 






 

 Where, x = 1, 2,…, 9
term
or
value
th
100
1
N
x
P
Percentile x 






 

 Where, x = 1, 2,…, 99
Where N is the number of observations (i.e. total frequency ∑f ).

7. Example: Calculate Q3 , D5 and P63 from the following data:
 
  .
16
16
16
75
.
0
16
term
th
75
term
th
76
75
.
0
term
th
75
term
th
75
.
75
term
th
4
1
100
3
term
th
4
1
N
3
Q
term
th
4
1
N
x
Q 3
x















 








 









 

Quartile
X 2 4 7 9 16 18 24
f 7 9 25 22 18 11 8
Solution: Data has been arranged in ascending order. Obtain less than type c.f.
X 2 4 7 9 16 18 24
f 7 9 25 22 18 11 8 N = 100
c.f 7 16 41 63 81 92 100
75th and 76th term included in

8.  
  .
9
9
9
5
.
0
9
term
th
50
term
th
51
5
.
0
term
th
50
term
th
5
.
50
term
th
10
1
100
5
term
th
10
1
N
5
D
term
th
10
1
N
x
D 5
x















 








 









 

Decile
X 2 4 7 9 16 18 24
f 7 9 25 22 18 11 8 N = 100
c.f 7 16 41 63 81 92 100
50th and 51th term included in

9.  
  .
41
.
13
9
16
63
.
0
9
term
th
63
term
th
64
63
.
0
term
th
63
term
th
63
.
63
term
th
100
1
100
63
term
th
100
1
N
63
P
term
th
100
1
N
x
P 63
x















 








 









 

Percentile
X 2 4 7 9 16 18 24
f 7 9 25 22 18 11 8 N = 100
c.f 7 16 41 63 81 92 100
63th term 64th term
Hence, Q3 = 16, D5 = 9 and P63 = 13.41 .

10. PARTITIONS VALUES FOR GROUPED DATA: Continuous frequency distribution
In the case of Continuous frequency distribution the computation of partitions values
involves the following steps:
1. Arranged the data in ascending order of magnitude (if not arranged).
2. Find the less than type cumulative frequencies (c.f.).
3. Convert the classes into exclusive form if given otherwise
4. Calculate the partitions values using following formulae.
Where, x = 1, 2, 3











 C
4
N
x
f
i
L
Q
Quartile 1
x
Where
L1 = lower limit of quartile class
N = total number of observations i.e. sum of frequencies
C = cumulative frequency of the class previous the quartile class
f = frequency of quartile class
i = class width i.e. Magnitude of quartile class
Quartile class: The class which contains [( x N)/4 ]th term.

11. Where, x = 1, 2,…,9











 C
10
N
x
f
i
L
D
Decile 1
x
Where
L1 = lower limit of Decile class
N = total number of observations i.e. sum of frequencies
C = cumulative frequency of the class previous the Decile class
f = frequency of Decile class
i = class width i.e. Magnitude of Decile class
Decile class: The class which contains [( x N)/10 ]th term.
Where, x = 1, 2,…,99











 C
100
N
x
f
i
L
P
Percentile 1
x
Where
L1 = lower limit of Percentile class
N = total number of observations i.e. sum of frequencies
C = cumulative frequency of the class previous the Percentile class
f = frequency of Percentile class
i = class width i.e. Magnitude of Percentile class
Percentile class: The class which contains [( x N)/100 ]th term.

12. Example: Calculate Q1 , D8 and P56 from the following data:
term
th
25
term
th
4
100
term
th
4
N
Q
term
th
4
xN
Q 1
x





























Quartile
Class 0-10 10-20 20-30 30-40 40-50 50-60 60-70 70-80
f 4 9 6 13 27 21 12 8
Solution:
Class 0-10 10-20 20-30 30-40 40-50 50-60 60-70 70-80 Total
f 4 9 6 13 27 21 12 8 ∑f = N = 100
c.f. 4 13 19 32 59 80 92 100
Hence,
Quartile Class = “30-40”
L1 = 30
N = 100
C = 19
f = 13
i = 40-30=10
Data has been arranged in ascending order. Obtain less than type c.f.
25th term included in
.
62
.
34
19
4
100
1
32
10
30
Q
C
4
N
x
f
i
L
Q
1
1
x

























13. term
th
80
term
th
10
100
8
term
th
10
xN
D
term
th
10
xN
D 8
x








 




















Decile
Class 0-10 10-20 20-30 30-40 40-50 50-60 60-70 70-80 Total
f 4 9 6 13 27 21 12 8 ∑f = N = 100
c.f. 4 13 19 32 59 80 92 100
Hence,
Decile Class = “50-60”
L1 = 50
N = 100
C = 59
f = 21
i = 60-50=10
80th term included in
.
60
59
10
100
8
21
10
50
D
C
10
N
x
f
i
L
D
8
1
x
























Putting
The
values

14. term
th
56
term
th
100
100
56
term
th
100
xN
P
term
th
100
xN
P 56
x








 




















Percentile
Class 0-10 10-20 20-30 30-40 40-50 50-60 60-70 70-80 Total
f 4 9 6 13 27 21 12 8 ∑f = N = 100
c.f. 4 13 19 32 59 80 92 100
Hence,
Percentile Class = “40-50”
L1 = 40
N = 100
C = 32
f = 27
i = 50-40=10
56th term included in
.
89
.
48
32
100
100
56
27
10
40
P
C
100
N
x
f
i
L
P
56
1
x
























Putting
The
values