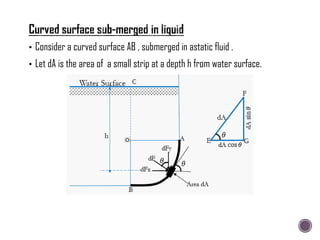
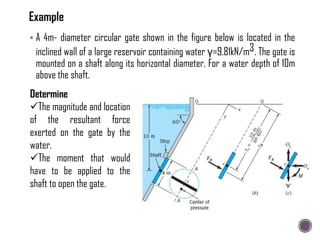
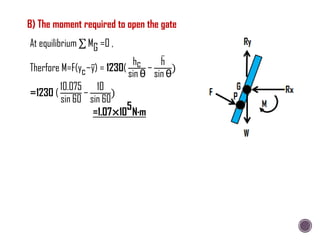
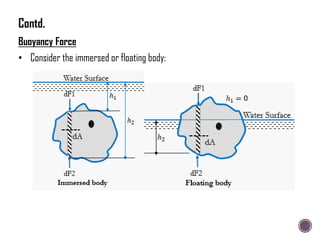
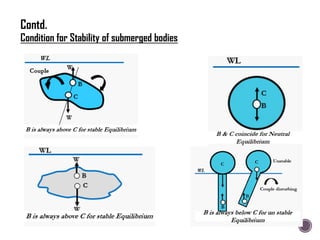
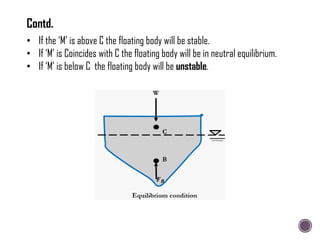
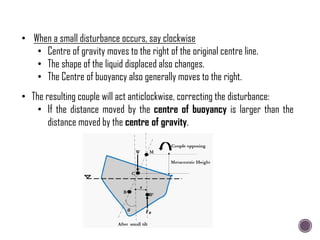
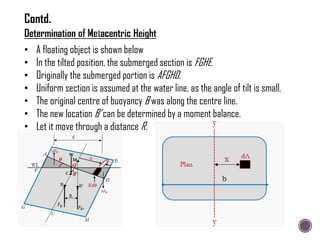
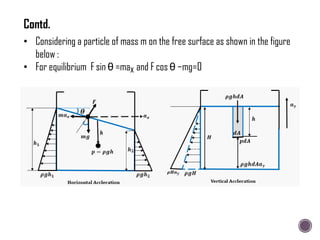
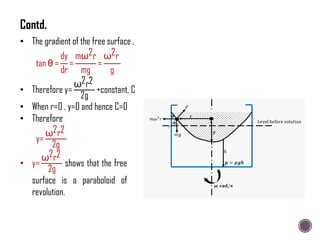
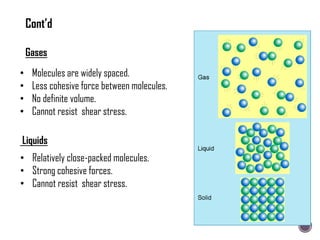
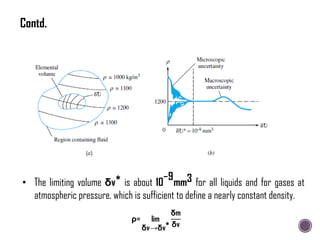
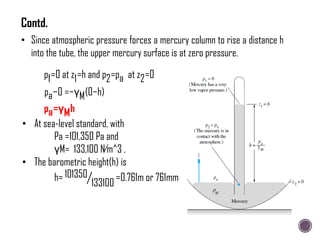
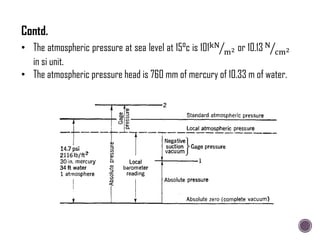
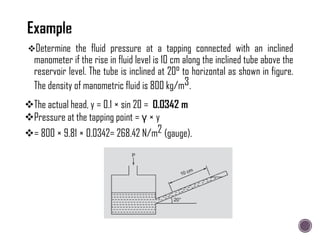
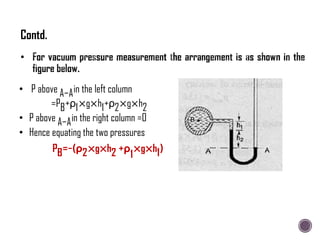
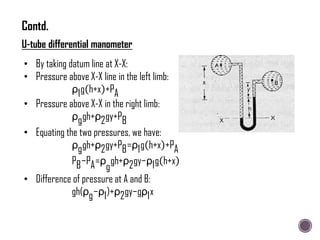
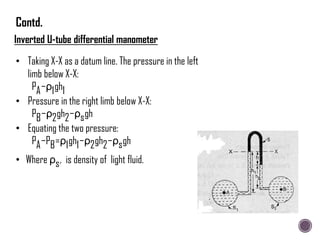
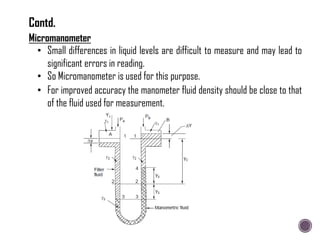
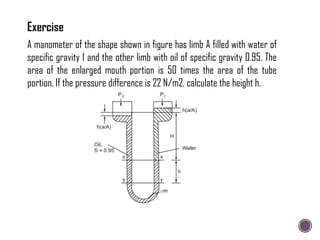
The document discusses the fundamental concepts of fluid mechanics, including the definitions and properties of fluids, including density, viscosity, and surface tension. It outlines the branches of fluid mechanics, specifically hydraulics, and describes the applications and significance of these properties in engineering, such as fluid flow, pressure variation, and hydrostatics. Key equations and principles like Pascal's Law and the relationship between shear stress and viscosity are also covered.

1. Department of Civil Engineering
CEng 2151
Getacher Teshome
Email: Abbiyteshome@gmail.com

2. • All matter consists of only two states, fluid and solid.
• There are two classes of fluids, liquids and gases.
• A Fluid is defined as a substance that deforms continuously when acted on by
a shearing stress of any magnitude.
• The existence of matter in these states is governed by the spacing between
different molecules and the intermolecular attractive forces.

3. Gases
• Molecules are widely spaced.
• Less cohesive force between molecules.
• No definite volume.
• Cannot resist shear stress.
• Relatively close-packed molecules.
• Strong cohesive forces.
• Cannot resist shear stress.
Liquids
Cont’d

4. • Any shear stress applied to a fluid, no matter how small, will result in motion of
that fluid.
• A fluid at rest must be in a state of zero shear stress.
A solid
• Resist a shear stress by a static deformation.
Contd.

5. • Fluid mechanics: is a branch of mechanics and studies about fluid(liquid +
Gasses).
• Hydraulics is a branch of fluid mechanics which studies about engineering
liquids i.e. most of the time water.
• It is the study of fluids either in motion (fluid dynamics) or at rest (fluid
statics).
• The principal concern of hydraulics is the study of fluids at rest and fluid flow
constrained by surrounding surfaces.
• It Studies about the kinematics, statics and dynamic aspects of fluids.
Contd.

6. Hydraulics studies flow in
• Open and closed channels
• Conduits
• Rivers
• Canals
• Flumes, as well as pipes, nozzles and hydraulic machines with internal
flow of fluids.
Contd.

7. Purposes of Hydraulics
• Design of wide range of Hydraulic structure (dams, canals weirs etc.) and
machinery (pumps, turbine etc.)
• Design of complex network of pumping and pipe lines for transporting liquids.
• Power generation.
• Flood protection.
• Surface and ground water studies.
• Flow metering like orifice meter.
• Pressure measurement.
Contd.

9.  Density
 Viscosity,
 Surface Tension
 Bulk Modulus
 and Vapor Pressure
The important properties are

10. The Fluid as a Continuum
• As far as we know, fluids are aggregations of molecules, widely spaced for
a gas, closely spaced for a liquid.
• Not practical/possible to treat fluid mechanics at the molecular level!.
• Instead, need to define a representative elementary volume (REV) to
average quantities like velocity, density, temperature, etc. within a
continuum.
• Continuum: smoothly varying and continuously distributed body of matter
– no holes or discontinuities.
• Simply means that its variation in properties is so smooth that the
differential calculus can be used to analyze the substance.
Contd.

11. What sets the scale of analysis?
• Too small: bad averaging
• Too big: smooth over relevant scales of variability
• For example fluid density, or mass per unit volume, has no precise meaning
because the number of molecules occupying a given volume continually changes.
• This effect becomes unimportant if the unit volume is large
• If the chosen unit volume is too large, there could be a noticeable variation in
the bulk aggregation of the particles.
• So that there is a limiting volume 𝛅𝐯∗
below which molecular variations may
be important and above which aggregate variations may be important.
Cont’d

12. • The limiting volume δv∗ is about 10
−9
mm3 for all liquids and for gases at
atmospheric pressure. which is sufficient to define a nearly constant density.
ρ= lim
δv→δv
∗
δm
δv
Contd.

13. • The density of a fluid is its mass
per unit volume.
• Density is highly variable in
gases and increases nearly
proportionally to the pressure
level.
Density or Mass Density( 𝝆)
Density(ρ)=
Mass of fluid(M)
Volume of fluid(V)
• Generally the density of a fluid is
dependent on temperature and
pressure.
Contd.

14. • For incompressible fluid density is nearly constant.
• liquids are about three orders of magnitude more dense than gases at
atmospheric pressure.
• The heaviest common liquid is mercury, and the lightest gas is hydrogen.
Fluid Density (𝑲𝒈
𝒎𝟑)
Water 998
Hydrogen 0.0838
Mercury 13580
Sea water 1030
Gasoline 660-690
Glycerin 1264
Table 1: Densities of common fluids at 20°C and 1 atm.
Contd.

15. • the weight of fluid per unit volume.
• Specific weight is very useful in the hydrostatic-pressure applications.
Specific Weight (or Unit Weight)(γ)
γ= W
V
,but W=mg, thus γ=ρg
Specific volume (Vs)
• Is the volume per unit mass.
• Not commonly used in fluid mechanics but it is used in
thermodynamics(Gas flow).
Vs= V
m = 1
ρ
Contd.

16. • Is the ratio of a fluid density to a standard reference fluid, water (for liquids), and
air (for gases)
• or the ratio of the mass of a fluid to the mass of an equal volume of pure water at
standard temperature and pressure.(normally at 4°C for water.
ρ=1000 Kg
m3
)
• Dimensionless.
SGgas=
ρgas
ρair
, ρair at 20°C
SGliquid=
ρliquid
ρwater
=
ρliquid
1000 Kg
m3
Specific Gravity(Relative density) (SG)
Contd.

17. Viscosity
• It is a measure of the resistance of a fluid to relative motion such as shear and
angular deformation within the fluid.
• plays a decisive role in laminar flow and fluid motion near solid boundaries.
• When a fluid is sheared, it begins to move at a strain rate inversely
proportional to a property called its coefficient of viscosity 𝛍.
• Viscosity of a fluid increases only
weakly with pressure. However,
Temperature has a strong effect.
• Viscosity increases as T increases
for gases.
• Viscosity decreases as T increases
for liquids.
Contd.

18. • The shear strain angle δθ will
continuously grow with time as long as
the stress τ is maintained.
• Fluids like water ,oil and air show a linear
relation between the applied shear and
the strain rate.
τ∝
δθ
δt
• From the figure Geometry ,tan δθ =
δuδt
δy
• Consider a fluid element sheared in one plane by a single shear stress τ.
• The relationship between viscous shear stress and viscosity is expressed by
Newton's law of viscosity.
Contd.

19. • In the limit of infinitesimal changes, tan δθ= dθ. this becomes a relation
between shear strain rate and velocity gradient.
dθ
dt
=
du
dy
• From τ∝
δθ
δt
, the applied shear is also proportional to the velocity gradient
for the common linear fluids.
• The constant of proportionality is the viscosity coefficient 𝛍.
• Then , τ=μ
dθ
dt
=μ
du
dy
• linear fluids which follows this equation called Newtonian fluids, after Sir
Isaac Newton (1687).
• Where, τ is the shear stress , μ is dynamic viscosity and
du
dy
is the velocity
gradient.
Contd.

20. • Gases and thin liquids (water, oil) tends to
be Newtonian fluids, while thick liquids like
mud, cream and cheese are Non-
Newtonian.
• Most fluids dealt in hydraulics are
Newtonian.
• In Newtonian fluid there is a linear relation between the magnitude of
applied shear stress and the resulting rate of deformation.
Contd.

21. • The shear stress is greatest at the wall. Further, at the wall, the velocity u is
zero relative to the wall: This is called the no-slip condition and is characteristic
of all viscous-fluid flows.
• After arranging the Newton‟s viscosity equation.
• du=
1
μ
τdy, by solving this differential equation
we can get the velocity distribution u(y).
• The graph representing velocity distribution is
shown below.
Contd.

22. Fluid 𝜇 (𝐾𝑔
𝒎𝒔) 𝜐(𝒎𝟐
𝒔)
Water 1×10
−3
1×10
−6
Hydrogen 8.8×10
−6
1.05×10
−4
Mercury 1.5×10
−3
1.16×10
−7
Gasoline 2.9×10
−4
4.22×10
−7
Glycerin 1.5×10
−1
1.18×10
−3
Table 2: Viscosity and Kinematic Viscosity of Fluids at 1 atm and 20°C
• The unit of dynamic viscosity μ is Ns
m2 or Kg
ms.
• A smaller unit of dynamic viscosity is called the poise.
1 poise = 1 g
cms= 0.1 Kg
ms .
• kinematics viscosity(𝛖): is the ratio of dynamic viscosity to density ( μ
ρ ).
• Unit of kinematic viscosity is Stoke, 1 Stoke= 0.0001m2
s
Contd.

23. Surface tension (𝛔)
• At the interface between a liquid and a gas, a film, or special layer, seems to
form on the liquid, apparently owing to the attraction of liquid molecules
below the surface.
• It is due to the cohesion b/n
molecules at the surface of a
liquid which adjoins another
immiscible liquid or gas.
• That property of the surface film to exert a tension is called the surface
tension.
• The magnitude of the tensile force per unit length of a line on the interface is
called surface tension σ, which has the unit N/m.
Contd.

24. • It is a simple experiment to place a
small needle on a quiet water surface
and observe that it will be supported
there by the film.
• Surface tension can be defined as the work in Nm
m2 or N/m required to
create unit surface of the liquid.
• The work is actually required for pulling up the molecules with lower energy
from below, to form the surface.
• When water molecules reach the surface they reach a dead end in the sense
that no molecules are present in great numbers above the surface to
attract or pull them out of the surface.
Contd.

25. • Surface tension is slight decrease with increasing temperature.
• Surface tension is only important where there is a free surface and the
boundary dimensions are small.
• surface tension effects are very pronounced in the case of tube of small bore
open to the atmosphere, capillary tubes, manometer tubes or open pores in
the soil.
Contd.

26. • Capillary attraction is caused by surface tension and by the relative value of
adhesion between liquid and solid to cohesion of the liquid.
• The action of surface tension in this case is to cause the liquid to rise within a
small vertical tube that is partially immersed in it. This phenomenon is called
capillarity.
Capillarity
Contd.

27. • Capillary attraction causes surface of mercury to depress down in the
capillary tubing when it is dipped in mercury. As shown in (ii)
Contd.

28. • Let D be the diameter of the tube and β is the contact angle.
• The surface tension forces acting around the circumference of the tube.
Surface tension force=σ×π×D
• The vertical component of this force =σ×π×D× cos β
• This is balanced by the fluid column of height, h.
• Taking the specific weight of liquid as γ. And then equating
h×γ×A=π×D×σ cos β, A= πD
2
4
h=
4σ cos β
ρgD
• Where ,h is the capillary rise in meter.
Contd.

29. • Pressure is a measure of force distribution over any
surface associated with the force.
• Pressure may be defined as the force acting along
the normal direction on unit area of the surface.
P= lim
A→a
∆F
∆A
= dF
dA
Vapor Pressure
• In the gaseous state the binding forces(Cohesive forces) are minimal.
• Due to this Molecules constantly escape out of a liquid surface and an equal
number constantly enter the surface when there is no energy addition.
Contd.

30. • Under equilibrium conditions these molecules above the free surface exert a
certain pressure.
• This pressure is known as vapor pressure corresponding to the temperature.
• The number of molecules escaping from the surface or re-entering will depend
upon the temperature
Cont’d
• Vapor pressure increases with temperature.
• Liquid will begin to boil if the pressure falls to
the level of vapor pressure corresponding
to that temperature.

31. Compressibility (1
K
) and Bulk Modulus (Evor K)
• It is the reciprocal of the bulk modules of elasticity (K).
• It is a measure of the instantaneous relative volume change of a fluid or
solid.
• The compressibility of a liquid is expressed by its bulk modulus of
elasticity.
• Bulk modulus, Ev is defined as the ratio of the change in pressure to the
rate of change of volume due to the change in pressure.
• It can also be expressed in terms of change of density.
Ev= (−dp)
(dv v)
= (−dp)
(dρ ρ)
Contd.

32. • With temperature the bulk modulus of liquids generally increases, reaches a
maximum and then decreases.
• In the case of gases the variation of volume, dv, with variation in pressure,
dp, will depend on the process( isothermal process and isentropic
process) used.
• The bulk modulus for liquids depends on both pressure and temperature.
• For water the maximum is at about
50°C.
• The bulk modulus is always positive
(N
m2
) why?
Bulk
modules
of
elasticity(Gpa)
Temprature °C
Contd.

33. Hydrostatics of Fluids

34. • Since there is no motion of a fluid layer relative to an adjacent layer, there are
no shear stresses in the fluid.
μ du
dy
=0
• Hydrostatics deals with the study of fluids that are at rest or are moving with
uniform velocity as a solid body so that there is no relative motion between
fluid elements
• Summation of forces must equal zero (no acceleration) in both the x and z
directions.
Engineering applications of hydrostatic principles
• the study of forces acting on submerged bodies such as gates, submarines,
dams etc.
• analysis of stability of floating bodies such as ships, pontoons etc.
Introduction

35. The force acting on the fluid particle is
• Due to the fluid normal to the surface
• Due to gravity( Self –weight of fluid particles)
• The pressure at a point is the limit of the ratio of normal force to area as the
area approaches zero size ,at the point
P= lim
A→a
∆F
∆A
= dF
dA

36. Pascal’s Law
• Pascal’s law which states that the pressure at a point in a fluid at rest is
equal in magnitude in all directions.
• According to Pascal, fluids under static conditions pressure is found to be
independent of the orientation of the area.
• So that, Tangential stress cannot exist if a fluid is to be at rest.
• To demonstrate pascal‟s law, a small wedge-shaped free body of unit length is
taken at the point (x, y) in a fluid at rest.
Contd.

37. • The only forces are the normal surface forces and gravity. So, the
equations of equilibrium in the x- and y-directions are, respectively.
pxδy−psδs sin θ =0
pyδx−psδs cos θ−γ
δxδy
2
=0
• In which ps, px, py are the average pressures on the three faces and γ is
the specific weight of the fluid.
• Allowing the inclined face to approach (x, y) means that reducing it to zero size
by maintaining the same angle θ, and using the geometric relations.
Weight of the wedge
δs cos θ =δx
δs sin θ =δy,
Contd.

38. The equations simplify to
pxδy−psδy=0
pyδx−psδx−γ
δxδy
2
=0
• The last term of the second equation is an infinitesimal of higher order of
smallness and may be neglected.
pxδy=psδy
Nearly Zero
pyδx=psδx
px=ps=py
• Since θ is any arbitrary angle, this equation proves that the pressure is the
same in all directions at a point in a static fluid.
Contd.

39. Pressure Variation In Static Fluid (Hydrostatic Law)
• It is necessary to determine the pressure at various locations in a
stationary fluid to solve engineering problems involving these situations.
• Pressure forces are called surface forces. Gravitational force is called
body force as it acts on the whole body of the fluid.
• Consider a small parallelepiped fluid element of size dx.dy.dz at any point in a
static mass of fluid as shown in the figure below.
Mid point (dx
2)

40. Fx=PAdz−PCdz =0
Equilibrium condition
Fz=PBdx−PDdx−dw =0
PA=P−
∂P
∂x
dx
2
PB=P−
∂P
∂z
dz
2
PC=P +
∂P
∂x
dx
2
PD=P +
∂P
∂z
dz
2
• Upon substitution the above equations becomes.
Fx= P−
∂P
∂x
dx
2
dz− P+
∂P
∂x
dx
2
dz =0 ⇒
∂P
∂x
=0
• Similarly
∂p
∂y
=0
• This means that there is no change in pressure with the horizontal(x) and (y)
direction.
Contd.

41. Fz= P−
∂P
∂z
dz
2
dx−γdzdx− P+
∂P
∂z
dz
2
dx =0
P−
∂P
∂z
dz
2
dx−γdzdx− P+
∂P
∂z
dz
2
dx =0
∂P
∂z
dzdx-γdzdx=0⇒
∂P
∂z
=−γ
∂P=−γ∂z
• After taking integral both side, P=−γZ+C
• Where C is a constant of integration and is equal to the pressure at z = 0.
Contd.

42. • In hydrostatics the law of variation of pressure with depth is usually written as;
P=γh+Po
• Where, h is measured vertically downward (i .e. h =-z) from a free surface, p is
the pressure at a depth h below the free surface and Po is the pressure at the
free surface.
• As we learned from the above equation the pressure at any point in a static
mass of liquid depends only up on the vertical depth of the point below the free
surface and the specific weight of the liquid.
• And it does not depend up on the shape & size of the bounding container.
Contd.

43. From the figure below
• Points a, b, c, and d are at equal depth in a horizontal plane and are
interconnected by the same fluid, water; therefore all points have the same
pressure.
• The same is true of points A, B, and C on the bottom.
• Pressure at points A,B,C and D is greater than from pressure at points a, b, c,
and d.
Contd.

44. By neglecting air pressure, calculate the pressure, in kPa ( gauge) , at A, B, C
and D in the figure bellow.
Patm

45. • There are two systems of pressure measurement.
• Absolute pressure
• Gauge pressure
• Absolute pressure: is the pressure which is measured with reference to
absolute vacuum pressure.
Pabs=Patm+Pgauge
• Gauge pressure: is defined as the pressure which is measured with the help of
pressure measuring device.
• Measured with reference to atmospheric pressure.
• Vacuum pressure( Absolute Zero pressure) is defined as the pressure below
the atmospheric pressure.
Pressure Measurement Systems

46. • Atmospheric pressure is the pressure exerted by an envelope of air
surrounding the earth's surface.
• The measurement of atmospheric pressure is usually accomplished
with a mercury barometer.
• A tube is filled with mercury and inverted while submerged in a
reservoir.
Mercury barometer
• This causes a near vacuum in the closed upper end because mercury
has an extremely small vapor pressure at room temperatures (0.16 Pa
at 20°C).
Contd.

47. • Since atmospheric pressure forces a mercury column to rise a distance h
into the tube, the upper mercury surface is at zero pressure.
p1=0 at z1=h and p2=pa at z2=0
pa−0 =−γM(0−h)
pa=γMh
• At sea-level standard, with
Pa =101,350 Pa and
γM= 133,100 N∕m^3 .
• The barometric height(h) is
h= 101350
133100
=0.761m or 761mm
Contd.

48. • The atmospheric pressure at sea level at 15°c is 101kN
m2 or 10.13 N
cm2
in si unit.
• The atmospheric pressure head is 760 mm of mercury of 10.33 m of water.
Contd.

49. • Liquid pressures are normally expressed with respect to the prevailing
atmospheric pressure and are called gage pressures.
• The pressure of a fluid is measured by:-
• Manometer
• Mechanical Gauge
Manometers
• Used to measure pressure in a fluid by balancing a column of fluid.
• They are suitable for measuring high pressure differences both positive and
negative, in liquids and gases.

50. Simple Manometer
Common types of Simple manometer
• Piezometer
• U-tube Manometer
• Single Column Manometer
Contd.

51. • A piezometer may be used to measure moderate positive pressures of liquids.
• One end of manometer is connected to the point where the pressure is to be
measured and other end is open to the atmosphere.
Glass Tube
Pipe
PA=γFluid in the glass×h (N
m2)
• The rise of liquid gives the pressure head at
that point.
Contd.

52. Determine the fluid pressure at a tapping connected with an inclined
manometer if the rise in fluid level is 10 cm along the inclined tube above the
reservoir level. The tube is inclined at 20° to horizontal as shown in figure.
The density of manometric fluid is 800 kg/m3.
The actual head, y = 0.1 × sin 20 = 0.0342 m
Pressure at the tapping point = γ × y
= 800 × 9.81 × 0.0342= 268.42 N/m2 (gauge).

53. • It consists of glass tube bent in u-shaped , one end of which is connected to a
point at which pressure is to be measured and other end remain open to the
atmosphere.
• The fluid in the glass tube has specific gravity grater than the liquid whose
pressure is to be determined.
• The most frequently used manometer liquids are mercury (specific gravity
13.6) and Alcohol (specific gravity 0.9).
• As the pressure the same for horizontal surface hence the pressure above the
datum line A-A in the left and the right column are the same.
Contd.

54. • P above A−Ain the left column =PB+ρ1×g×h1
• P above A−Ain the right column =ρ2×g×h2
• Hence equating the two pressures
PB=ρ2×g×h2 −ρ
1
×g×h1
Contd.

55. • P above A−Ain the left column
=PB+ρ1×g×h1+ρ2×g×h2
• P above A−Ain the right column =0
• Hence equating the two pressures
PB=−(ρ2×g×h2 +ρ
1
×g×h1)
Contd.

56. • Is a modified form of U-tube Manometer.
• A reservoir is connected to the one limb having a cross-section area
100times of the area of a tube.
• For heavy liquid in the reservoir will cause a rise of heavy liquid level in the
right limb
A×∆h=a×h2
∆h=
a×h2
A
Contd.

57. • After Substituting ∆h,
PA=
a×h2
A
ρ2g−ρ1g +h2ρ2g−h1ρ1g
ρ2×g×(∆h+h2)
• pressure in the left limb will be
ρ1×g×(∆h+h1)+PA
ρ1×g×(∆h+h1)+PA=ρ
2
×g×(∆h+h2)
• Equating these pressures, We have
But, ∆h=
a×h2
A
• Considering datum Y-Y, the pressure in the right limb will be
Contd.

58. • Differential manometer are devices used for measuring the difference
between two points in a pipe or in two different pipes. .
• It consists of a U-tube , containing a heavy liquid. Whose two ends are
connected to the points. Whose difference of pressure is to be
measured.
• Most common types are:
• U-tube differential manometer
• Inverted U-tube differential manometer
Contd.

59. U-tube differential manometer
• By taking datum line at X-X:
• Pressure above X-X line in the left limb:
ρ1g h+x +PA
• Pressure above X-X in the right limb:
ρggh+ρ2gy+PB
• Equating the two pressures, we have:
ρggh+ρ2gy+PB=ρ1g h+x +PA
PB−PA=ρ
g
gh+ρ2gy−ρ1g h+x
• Difference of pressure at A and B:
gh(ρg−ρ1)+ρ2gy−gρ1x
Contd.

60. Inverted U-tube differential manometer
• Taking X-X as a datum line. The pressure in the left
limb below X-X:
PA−ρ1gh1
• Pressure in the right limb below X-X:
PB−ρ2gh2−ρsgh
• Equating the two pressure:
PA−PB=ρ1gh1−ρ2gh2−ρsgh
• Where ρs, is density of light fluid.
Contd.

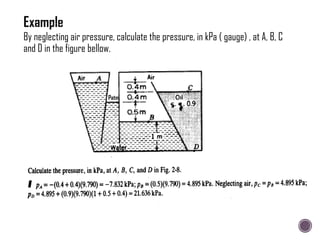
61.  An inverted U-tube manometer is fitted between two pipes as shown in
Figure. Determine the pressure at E if PA = 0.4 bar or 40kPa (gauge).
 PB = PA – [(0.9 × 1000) × 9.81 × 1.2]
= 40000 – [(0.9 × 1000) × 9.81 × 1.2]
= 29,405.2 N/m2
 PC = PB – [(0.9 × 1000) × 9.81 ×
0.8] = 22342 N/m2
 PD =PC = 22342 N/m2
 PE = PD + [1000 × 9.81 × 0.8] =
30190 N/m2 = 30.19 kPa (gauge)

62. Micromanometer
• Small differences in liquid levels are difficult to measure and may lead to
significant errors in reading.
• So Micromanometer is used for this purpose.
• For improved accuracy the manometer fluid density should be close to that
of the fluid used for measurement.
Contd.

63. Starting from level in chamber A and level 3 as datum
PB=PA+ y1+∆y γ1 + y2+y3−∆y ×y2 − 2y3×γ3 − y2−y3+∆y ×γ2 −{(y1−∆y)×γ1}
PB =PA −{ 2×y3× γ3−γ2 +2∆y×(γ2−γ1)}
• Let pressure PA>PB and let it cause a depression of ∆y in chamber A. The
fluid displaced goes into the U tube limb of area a.
• The displacement in the limb will therefore by (y × A/a) which becomes
better readable.
• There fore the displaced volume of fluid:
ay3=∆yA
∆y= (a A)y3
PA−PB=2×y3×[γ3−γ2×{1−( a A)}]
• Very often γ1 is small (because gas is generally the medium) and the last
term is negligible. So
Contd.

64. A manometer of the shape shown in figure has limb A filled with water of
specific gravity 1 and the other limb with oil of specific gravity 0.95. The
area of the enlarged mouth portion is 50 times the area of the tube
portion. If the pressure difference is 22 N/m2, calculate the height h.

65. Hydrostatic Forces on Plane and Curved
Surfaces

66. • When a fluid is in contact with a surface it exerts always a normal force
on the surface.
• The walls of reservoirs, sluice gates, flood gates, oil and water tanks
and the hulls of ships are exposed to the forces exerted by fluids in
contact with them.
• For the design of such structures it is necessary to determine
• the total force on them.
• the point of action of this force.
• The point of action of the total force is known as Centre of pressure or
pressure Centre.
• Centre of pressure is defined as the point of application of the total
pressure on the surface .
Introduction

67. Centroid and Moment of Inertia of Areas
• In the process of obtaining the resultant force and Centre of pressure, the
determination of first and second moment of areas is found necessary and
hence this discussion.
NB:
• Centre of gravity of a body is the point through which the resultant
gravitational force (Weight) of the body acts for any orientation of the
body.
• Centroid is the point in a plane area such that the moment of the area ,
about any axis through that point is zero.
Contd.

68. • Moment about y axis= xdA
• Moment about x axis= ydA
• The moment of the area with respect to the y axis can be obtained by:
• Summing up the moments of elementary areas(dA) all over the surface
with respect to this axis as shown in Figure below.
• Moment about the new axis
= (x−k)dA
• Moment about the new axis
= x dA− kdA
Contd.

69. • When k=x , the moment will be about the centroidal y axis. so it is zero since
summation of moment throug the center of gravity is always zero.
0= x dA− xdA
x=
xdA
A
• Similarly the centroidal x axis passing at y can be located using:
y=
ydA
A
• The point of intersection of these centroidal axes is known as the centroid
(x, y) of the area.
Contd.

70. • Considering an axis parallel to both x and y axis through the centroid.
and its moment of inertia represented by IG:
• Second moment or moment of inertia of an area with respect to the x and
y axis.
Ix= y2dA
Iy= x2dA
• Parallel Axis Theorem
Contd.

71. IG= (y−y)
2
dA
IG= y2dA− 2y ydA + y2dA
By definition y2dA =Ix, ydA =yA,
Since y2is constant, y2dA =y2A therefore
IG=Ix−2y
2
A+y2A
Ix=IG+y2A
Similarly Iy=IG+x2A
• Similarly the product of inertia is defined as:
Ixy= xydA =IGxy+xyA
If any one of the axes is an axis of
symmetry for the area, Ixy = 0.
Contd.

72. Table 3: The moment of inertia and center of gravity for some important plane surface
Descripti
on
C.G. from the
base
Area IG MI about
base (Io)
Rectangle
x=
b
2
A=ba ba
3
12
ba
3
3
Triangle
x=
h
3
A=
bh
2
bh
3
36
bh
3
12
Circle
x=
d
3 A=
πd
2
4
πd
4
64
-
--
Trapezium
x=(
2a+b
a+b
)
h
3
(
a+b
2
)×h
(
a2+4ab+b
2
36 a+b
)
____
Contd.

73. Hydrostatic Forces on Plane Surfaces
• The submerged surface may be:
• Vertical plane surface
• Horizontal plane surface
• Inclined plane surface

74. Total pressure (F): the total pressure on the surface may be determined by
dividing the entire surface in to a number of small parallel strips.
• Consider a strip of thickness dh and width b at a depth h from free surface
of liquid as shown in the figure.
Vertical plane surface submerged in a liquid

75. • Pressure intensity on the strip, ρgh
Area of strip, dA=b×dh
• Total pressure force on the strip, dF=p×Area
dF=ρgh×dh×b
• Total pressure force on the whole surface,
F= dF = ρgh×b×dh=ρg b×h×dh
• But b×h×dh = hdA
hdA =Ah
F=ρgAh
Contd.

76. • Centre of pressure(hc) is calculated by using “Principle of moments”
which states that the moment of force about an axis is equal to the sum of
moments of the components about the same axis.
• Means that Fhc= dFh
• Moment of force dF acting on a strip about the free surface liquid
=dF×h
=ρgh×b×dh×h
• Sum of moment of all such forces about free surface of liquid
= ρgh×b×dh×h =ρg b×h×hdh
=ρg b×h
2
dh=ρg h
2
dA
• But, h
2
dA= bh
2
dh =Moment of inertia about free surface(Io)
• Sum of moments about free surface =ρgI0
Contd.

77. Fhc=ρgI0
• But F=ρgAh
• Therefore, ρgAh×hc=ρgI0
hc=
ρgIo
ρgAh
=
Io
Ah
• From parallel axis theorem Io=IG+A×h
2
• Substituting in to Io,
hc=
IG
Ah
+h
Contd.

78. • In case of horizontal surface as every point of the surface is at the same
depth from the free surface of the liquid , the pressure intensity will be
equal on the entire surface.
p=ρgh
• The total force F=p×A
F=ρgh×A=ρghA
• Similarly h=hc
F=ρghA

79. • Consider a small strip of area dA at a depth ‘h’ from free surface and at a
distance y from the axis O-O.

80. h=y sin θ
F= ρg×y sin θ×dA =ρg× sin θ ydA
• But ydA =Ay
• Where y=distance of C.G. from axis O-O
F=ρg× sin θAy
F=ρg×Ah
• Total pressure force on the whole area, F= dF = ρghdA
• But from the figure ,Trigonometry ,
h
y
=
h
y
=
hc
yc
=sin θ
• Pressure intensity on the strip p=ρgh
• Therefore pressure force, dF , on the strip, dF=p×Area of strip
dF= ρgh×dA
Contd.

81. • Presuure force on the strip, dF=ρg×y sin θ×dA
• Moment of the force ,dF , about axis O-O
• Moment=dFy=ρg×y2 sin θ×dA
• Sum of moments of all such forces about O-O
• Sum of moments= ρg×y2 sin θ×dA =ρg× sin θ y2dA
y2dA=M.O.I. of the surface about O-O =I0
• Sum of moments= ρg sin θ I0
• Moment of the total force , F, about O-O=F×yc
• Equating the two moments, ρg sin θ I0 =F×yc
yc=
ρg sin θ I0
F
• then driving a relation for center of pressure (hc) using parallel axis
theorem: Io=IG+Ay2
Contd.

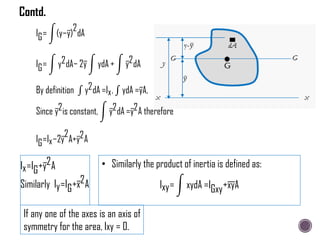
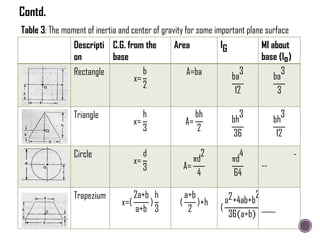
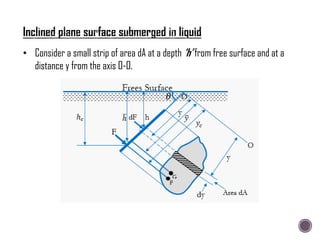
82. hc
sin θ
=
ρg sin θ
ρgAh
[IG+Ay
2
]
hc=
sin2 θ
Ah
[IG+Ay
2
]
But
h
y
= sin θ
hc=
sin2 θ
Ah
[IG+
Ah
2
sin2 θ
]
hc=
IG sin2 θ
Ah
+h
Contd.

83. • Consider a curved surface AB , submerged in astatic fluid .
• Let dA is the area of a small strip at a depth h from water surface.

84. •Then the pressure intensity on the area dA is ρgh.
•And the pressure force dF=p×Area=ρgh×dA
•This force dF acts normal to the surface.
•Hence the total pressure force on the curved surface should be
F= ρghdA
• BY Resolving the force dF in to dFx and dFy and integrating, Fx and Fy will be
obtained.
• The total force on the curved surface:
F= Fy
2
+Fx
2
• And The inclination of the resultant from the horizontal:
tan ϕ =
Fy
Fx
Contd.

85. • Resolving the force dF in x and y directions.
dFx=dF sin θ =ρghdA sin θ
dFy=dF cos θ =ρghdA cos θ
• And The forces in x and y directions are:
Fx= dFx = ρghdA sin θ =ρg hdA sin θ
Fy= dFy = ρghdA cos θ =ρg hdA cos θ
• Both, Fx and Fy are acts on the projected
area of dA:
Contd.

86. • Projected areas are dA cos θ and dA sin θ.
• So, hdA cos θ will be the volume of liquid contained in the elementary area dA
up to the free surface of the liquid.
• Thus hdA cos θ is the total volume contained between the curved surface
extended up to free surface.
• Hence ρg hdA cos θ is the total weight supported by the curved surface.
Thus:
Fy=ρg hdA cos θ , Fy=ρg dV =γV, Fx=ρg hdA sin θ =γhAv
Point of application of Fx, hc=
IG
Ah
+h
Contd.

87.  A 4m- diameter circular gate shown in the figure below is located in the
inclined wall of a large reservoir containing water γ=9.81kN/m3. The gate is
mounted on a shaft along its horizontal diameter. For a water depth of 10m
above the shaft.
Determine
The magnitude and location
of the resultant force
exerted on the gate by the
water.
The moment that would
have to be applied to the
shaft to open the gate.

88. F=γhA
h = 10m which is given
Then F=γhA=(9.81kN/m3)(10m)(
𝜋(4)2
4
m2)
F=1230kN
Center of pressure
hc=
IG sin2 θ
Ah
+h
IG =
πd
4
64
=
π(4)
4
64
= 12.57m4
hc=
IG sin2 θ
Ah
+h
hc=
IG sin2 θ
Ah
+h =
12.57 (sin 60)
2
(12.57)(10)
+10=10.075m
A) Magnitude of hydrostatic pressure force on the circular area:

89. B) The moment required to open the gate
At equilibrium MG =0 ,
Therfore M=F(yc−y) = 1230(
hc
sin θ
−
h
sin θ
)
=1230 (
10.075
sin 60
−
10
sin 60
)
=1.07×10
5
N∙m

90. • Studying forces due to fluid on floating and submerged bodies is important in the
design of boats, ships, balloons and submersibles and also hydrometers.
• If an object is immersed in or floated on the surface of fluid under static
conditions a force acts on it due to the fluid pressure. This force is called buoyant
force.
• Buoyant force:
• Resultant pressure force acting on the surface of a volume partially or
completely surrounded by one or more fluids under non flow conditions.
• Acts vertically on the volume.
• Equal to the weight of the displaced fluid and acts upwards through the centre
of gravity of the displaced fluid.
• Acts at a point called center of buoyancy.
Buoyancy Forces and Stability of Floating Bodies

91. •Buoyant force calculation is based on Archimedes principle.
•Archimedes principle can be stated as:
(i) a body immersed in a fluid is buoyed up by a force equal to the weight of
the fluid displaced and
(ii) a floating body displaces its own weight of the liquid in which it floats.
Contd.

92. Buoyancy Force
• Consider the immersed or floating body:
Contd.

93. • Net force on the element
(dF2−dF1)=γdA(h2−h1)=γdV.
• Where dV is the volume of the element . This force acts upwards. As (h2>h_1 ).
• Summing up over the volume , F=γV (or)the weight of the volume of liquid
displaced.
• Incase of floating body:
dF2−dF1=γdAh2=γdV
Contd.

94. • Three possible situations for a body when immersed in a fluid
Let W= weight of immersed body
w = weight of the liquid of equal volume
I. If W>w the body will sink into the liquid.
• To keep it floating additional upward force is required).
II. If W=w the body will submerge and may stay at any location below the
surface.
III. If W<w then the body will be partly submerged and will float in the liquid.
Practical examples:
• A submarine (W=w)
• ship (W<w)
Contd.

95. • Equilibrium of a body exists when there is no resultant force or moment on the
body.
• A body can stay in three states of equilibrium.
I. Stable equilibrium: Small disturbances will create a correcting couple and
the body will go back to its original position prior to the disturbance.
II. Neutral equilibrium: Small disturbances do not create any additional
force and so the body remains in the disturbed position. No further change
in position occurs in this case.
III. Unstable equilibrium: A small disturbance creates a couple which acts to
increase the disturbance and the body may tilt over completely.
Contd.

96. • Exists when two forces of equal magnitude acting along the same line of action,
but in the opposite directions exist on a floating/submerged body.
• Equilibrium exists when gravitational force and buoyant force are equal and
opposite and act along the same line.
Contd.

97. Condition for Stability of submerged bodies
Contd.

98. Conditions for The Stability of Floating Bodies
• When B is above C the floating body is always stable.
• When B coincides with C, the two forces acts at the same point . the body
just remain in the disturbed position.
• When B is below C additional analysis is required to establish stable
condition. Which is Metacentric height.
• NB: For a floating body, the center of buoyancy need not be located
above the center of gravity for stability.
• Metacenter :The location „M‟ at which the line of action of buoyant force
meets the centroidal axis of the body, when disturbed.
• Metacentric height: The distance of metacenter from the centroid of the
body.
Contd.

99. • If the „M‟ is above C the floating body will be stable.
• If „M‟ is Coincides with C the floating body will be in neutral equilibrium.
• If „M‟ is below C the floating body will be unstable.
Contd.

100. • When a small disturbance occurs, say clockwise
• Centre of gravity moves to the right of the original centre line.
• The shape of the liquid displaced also changes.
• The Centre of buoyancy also generally moves to the right.
• The resulting couple will act anticlockwise, correcting the disturbance:
• If the distance moved by the centre of buoyancy is larger than the
distance moved by the centre of gravity.

101. • If the distance moved by the centre of gravity is larger, the couple will be
clockwise and it will tend to increase the disturbance or tilting.
Contd.

102. • A floating object is shown below
• In the tilted position, the submerged section is FGHE.
• Originally the submerged portion is AFGHD.
• Uniform section is assumed at the water line, as the angle of tilt is small.
• The original centre of buoyancy B was along the centre line.
• The new location B‟ can be determined by a moment balance.
• Let it move through a distance R.
Contd.

103. • The force system consists of the original buoyant force acting at B and the
forces due to the wedges and the resultant is at B’ due to the new location of
the buoyant force.
• Taking moments about B, ∆FB × S = W × R.
• The moment ∆FB × S can be determined by taking moment of elements
displaced about O, the intersection of water surface and centre line.
• Consider a small element at x with area dA.
• The height of the element = xtanθ. For small angle θ it can be expressed by
xθ. (θ is expressed in radian).
• The mass of the element= γxθ dA and moment distance is x.
∆FB × S= γx2θ dA
∆FB × S= γθ x2 dA
Contd.

104. ∆FB × S= γx2θ dA
∆FB × S=γθIy
W × R=γθIy
γV × R=γθIy, but W = γV where V is the displaced volume.
• From the triangle MBB′, R = MB sinθ or R= MB θ.
MB=
R
θ
=
Iy
V
=
(1
12
)Lb
3
V
• Both Iy and V are known. As V = W/γ, the metacentric height is given by,
(Metacentric height) MC=MB±CB
• CB is originally specified. So the metacentric
height can be determined.
• If C is above B –ve sign is used. If C is below B
+ve sign is to be used.
• Hence the righting couple
Contd.
γVMCθ=WMC sin θ

105. Relative Equilibrium of Liquids states that:
• If a liquid is contained in a vessel which is at rest, or moving with constant linear
velocity.
• It is not affected by the motion of the vessel.
• the pressure distribution is hydrostatic.
• If the container is given a continuous and constant linear acceleration or is
rotated about a vertical axis with uniform angular velocity.
• The liquid will eventually reach an equilibrium situation.
• The liquid move as a solid body with no relative motion between the fluid
particles and the container.
• shear stress does not exist and the laws of fluid statics still apply .

106. • The two cases of practical interest are:
1) Uniform linear acceleration
2) Uniform rotation about a vertical axis.
Contd.

107. 1) Uniform linear acceleration
• A liquid in an open vessel subjected to a uniform acceleration adjusts to the
acceleration after some time so that it moves as a solid and the whole mass
of liquid will be in relative equilibrium.
• A horizontal ax causes the free liquid surface to slope upward in a direction
opposite to ax and the entire mass of liquid is then under the action of:
• gravity force
• hydrostatic forces
• and the accelerating or inertial force max.
• m being the liquid mass.

108. • Considering a particle of mass m on the free surface as shown in the figure
below :
• For equilibrium F sin θ =max and F cos θ −mg=0
Contd.

109. • Therefore slope of free surface ,
tan θ =
max
mg =
ax
g
• And the lines of constant pressure will be parallel to the free liquid surface.
• A vertical acceleration which is positive upward 𝐚𝐲 causes no disturbance to
the free surface and the fluid mass is in equilibrium.
• For equilibrium of a small column of liquid of area dA:
PdA=ρhdAg+ρhdAay
•Therefore P, pressure intensity at adept h below the free surface.
P=ρgh(1+
ay
g )
Contd.

110. • Fluid particle moving in a curved path experience a radial acceleration .
• When a cylindrical container partly filled with a liquid is rotated at a constant
angular velocity 𝝎 about a vertical axis the rotational motion is transmitted
to different parts of the liquid and after some time the hole fluid mass.
• Assume the same angular velocity as a solid and the fluid particles
experience no relative motion.
• A particle of mass, m, on the free surface is in equilibrium under the action
of:
• Gravity
• Hydrostatic force
• The centrifugal acceleration due to rotation.
Contd.

111. • The gradient of the free surface ,
tan θ =
dy
dr
=
mω2r
mg
=
ω2r
g
• Therefore y=
ω2r2
2g
+constant, C
• When r=0 , y=0 and hence C=0
• Therefore
y=
ω2r2
2g
• y=
ω2r2
2g
shows that the free
surface is a paraboloid of
revolution.
Contd.