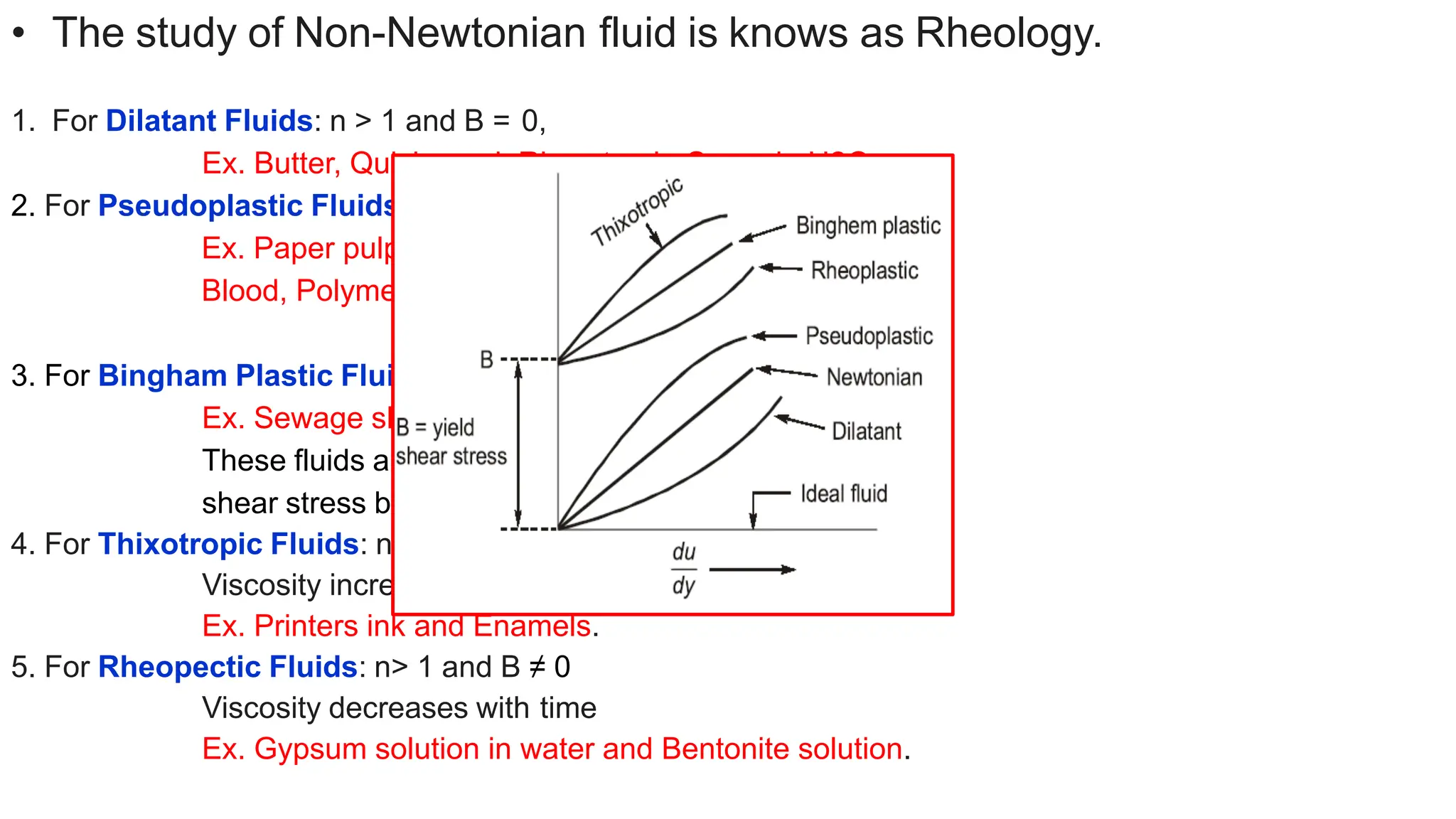
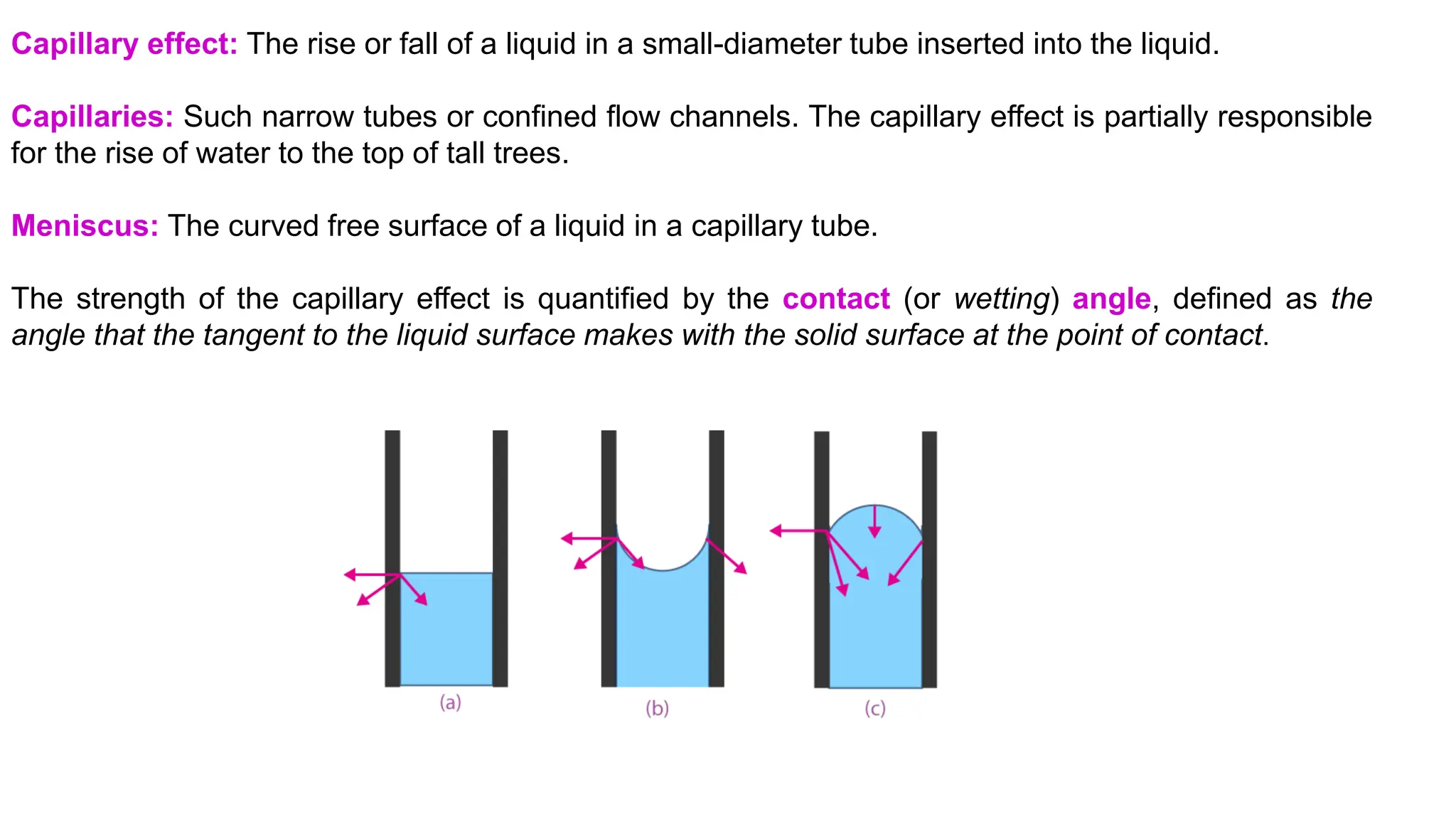
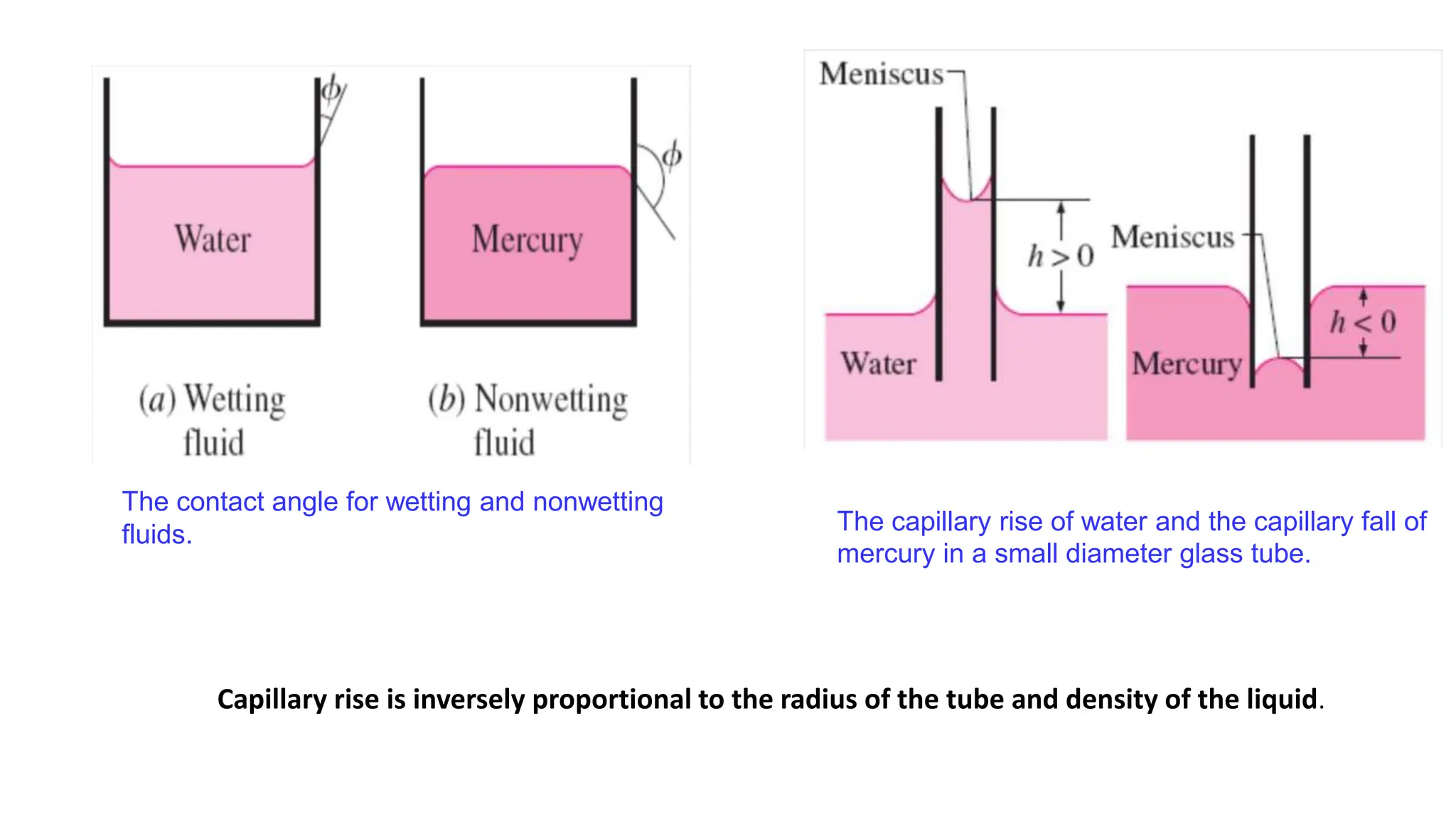
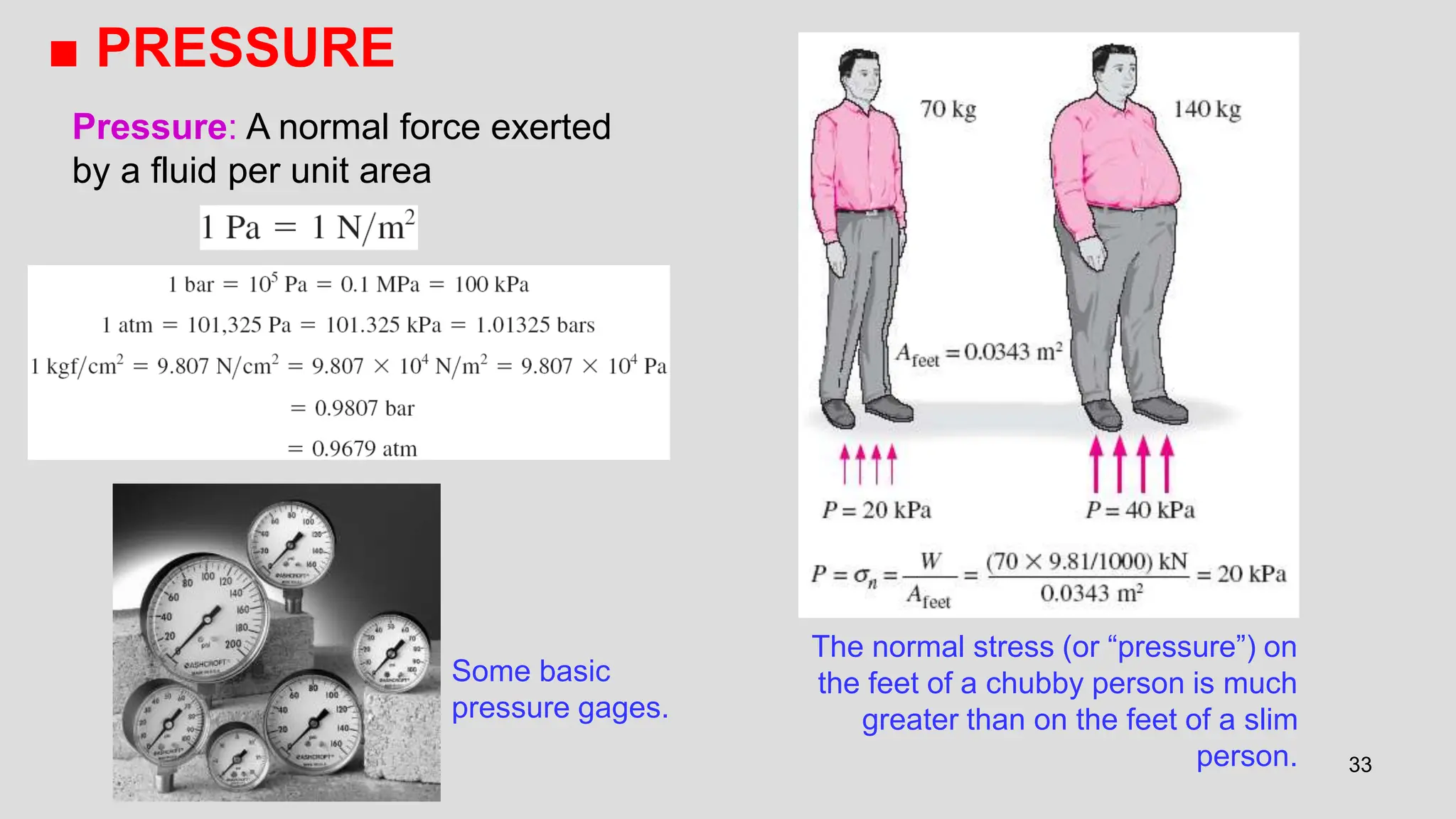
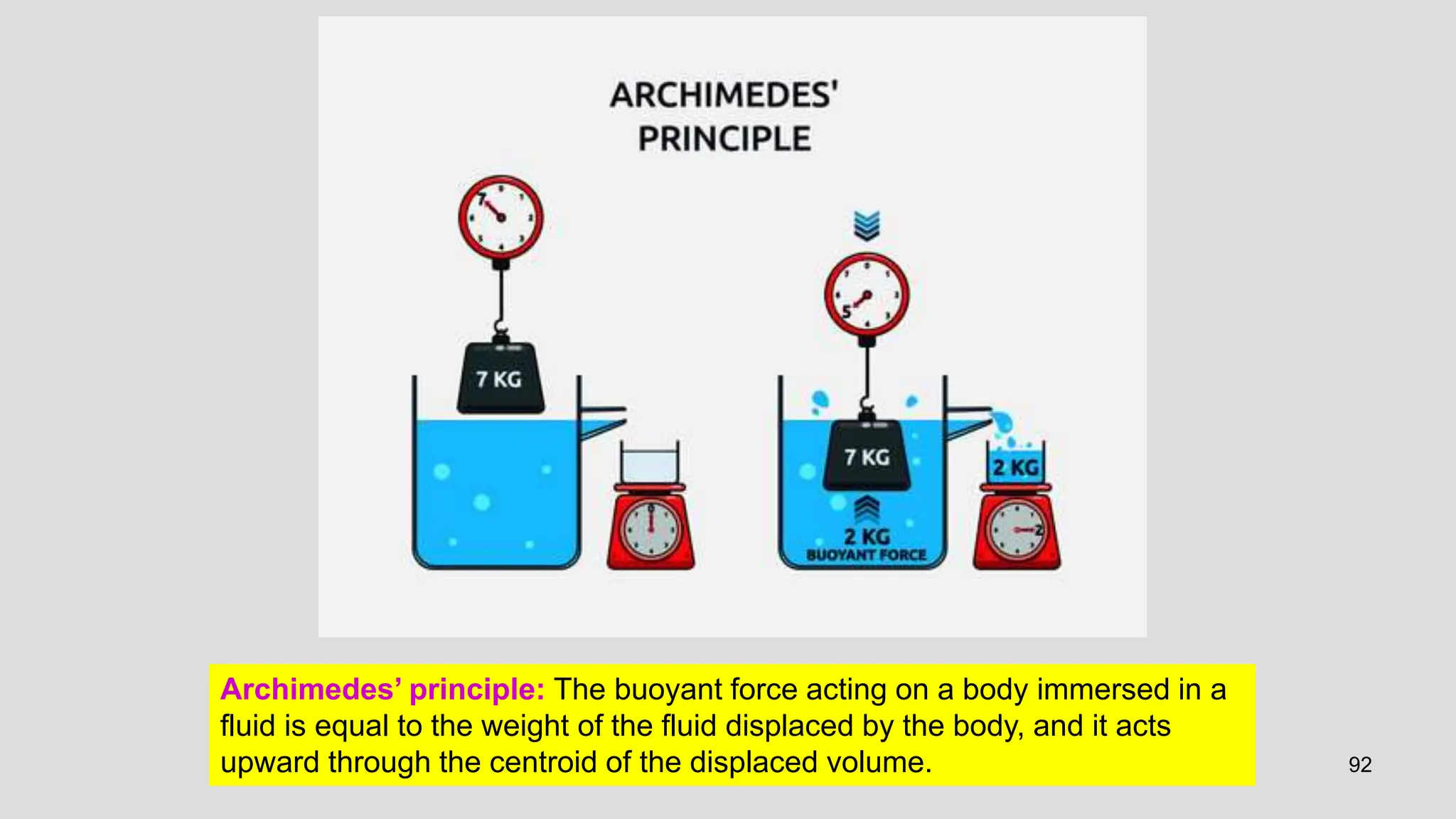
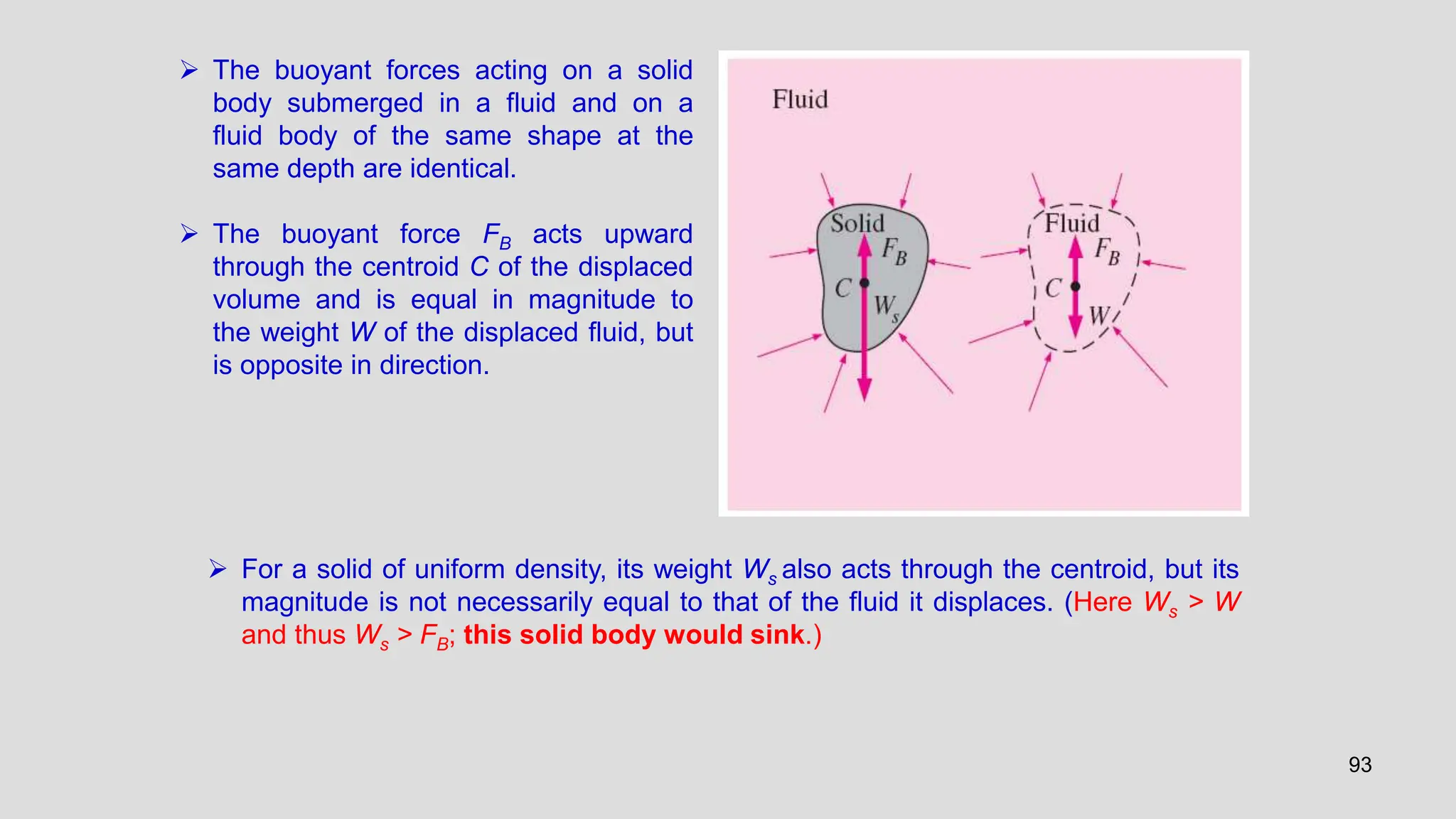
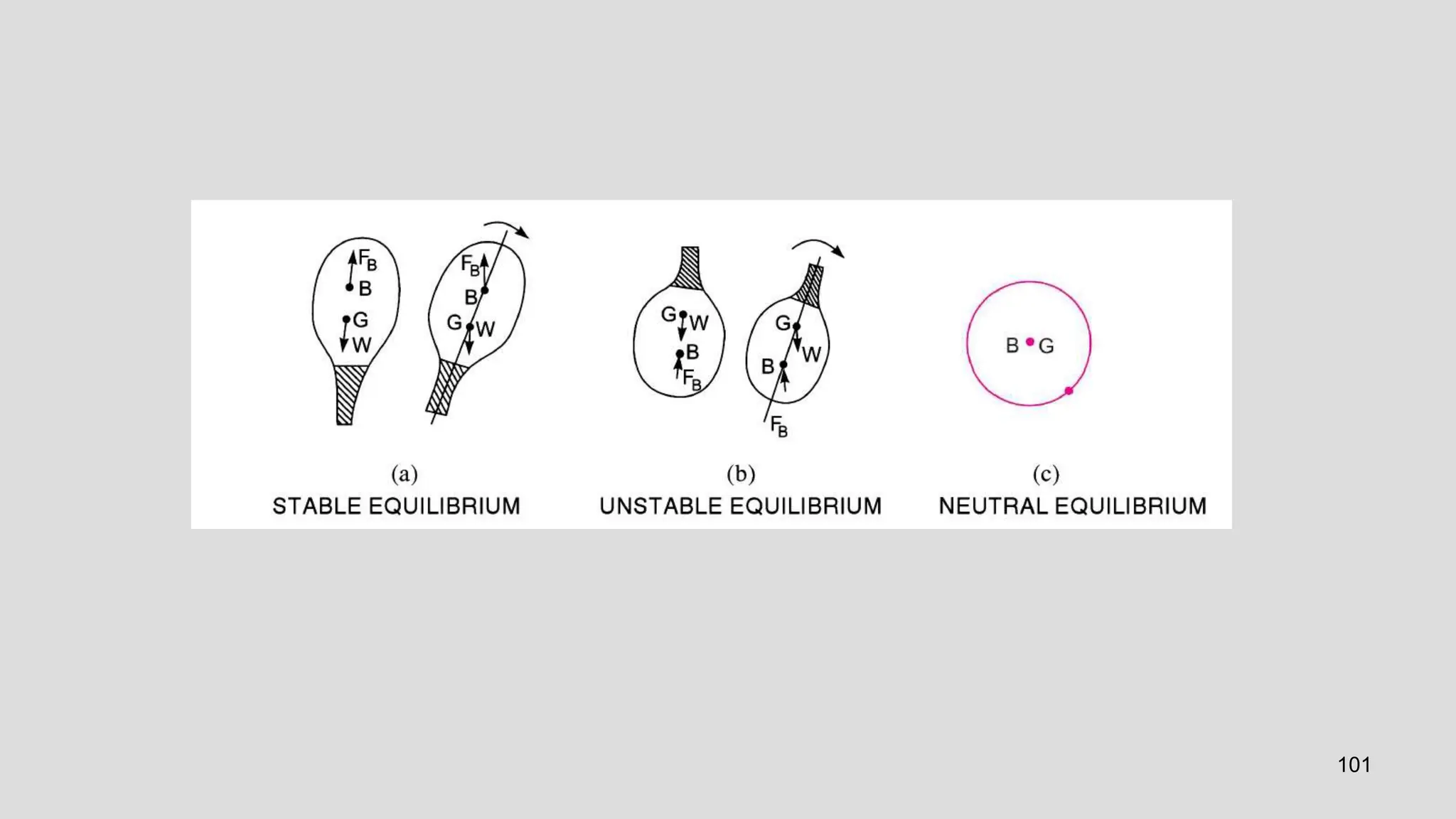
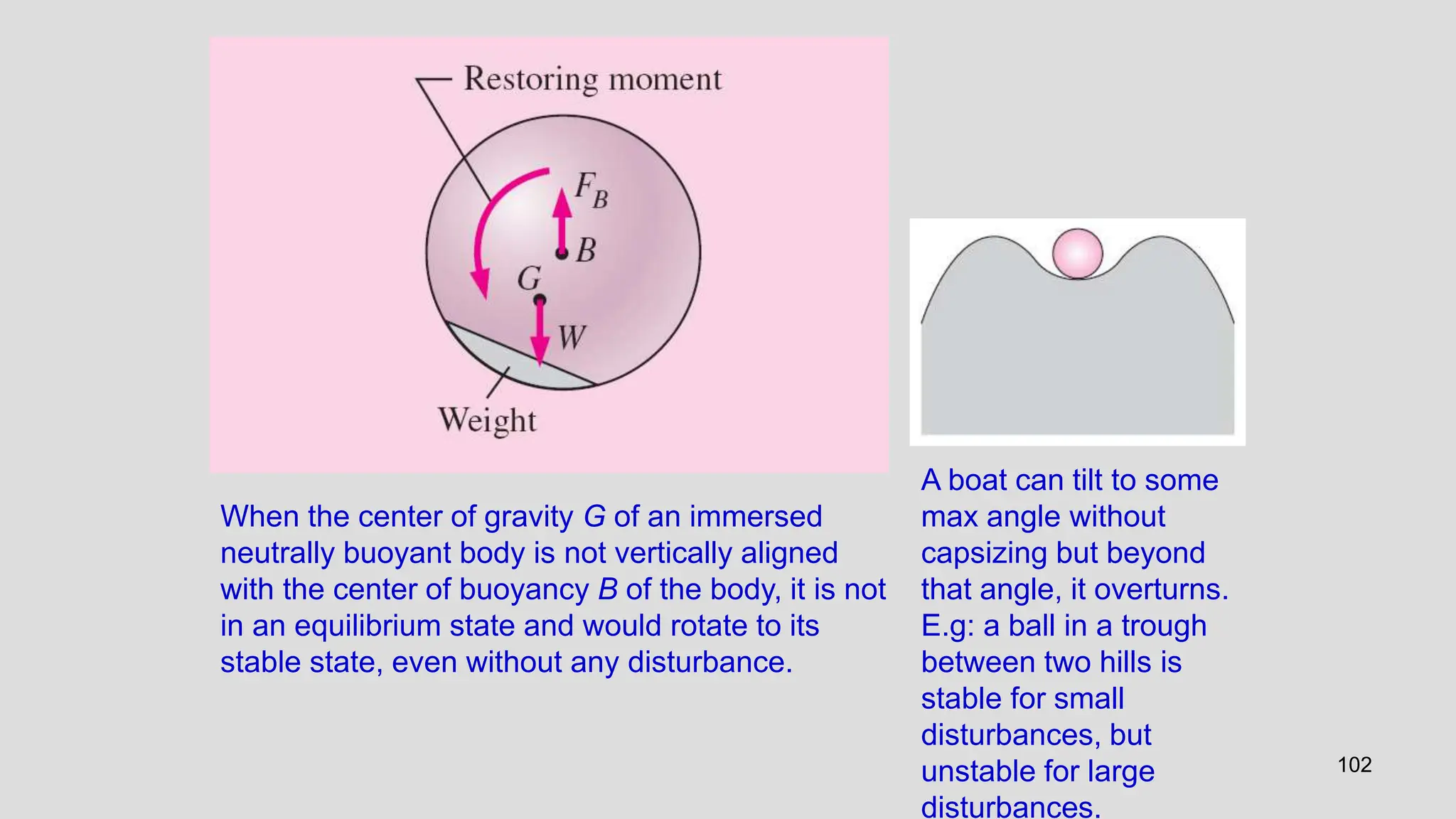
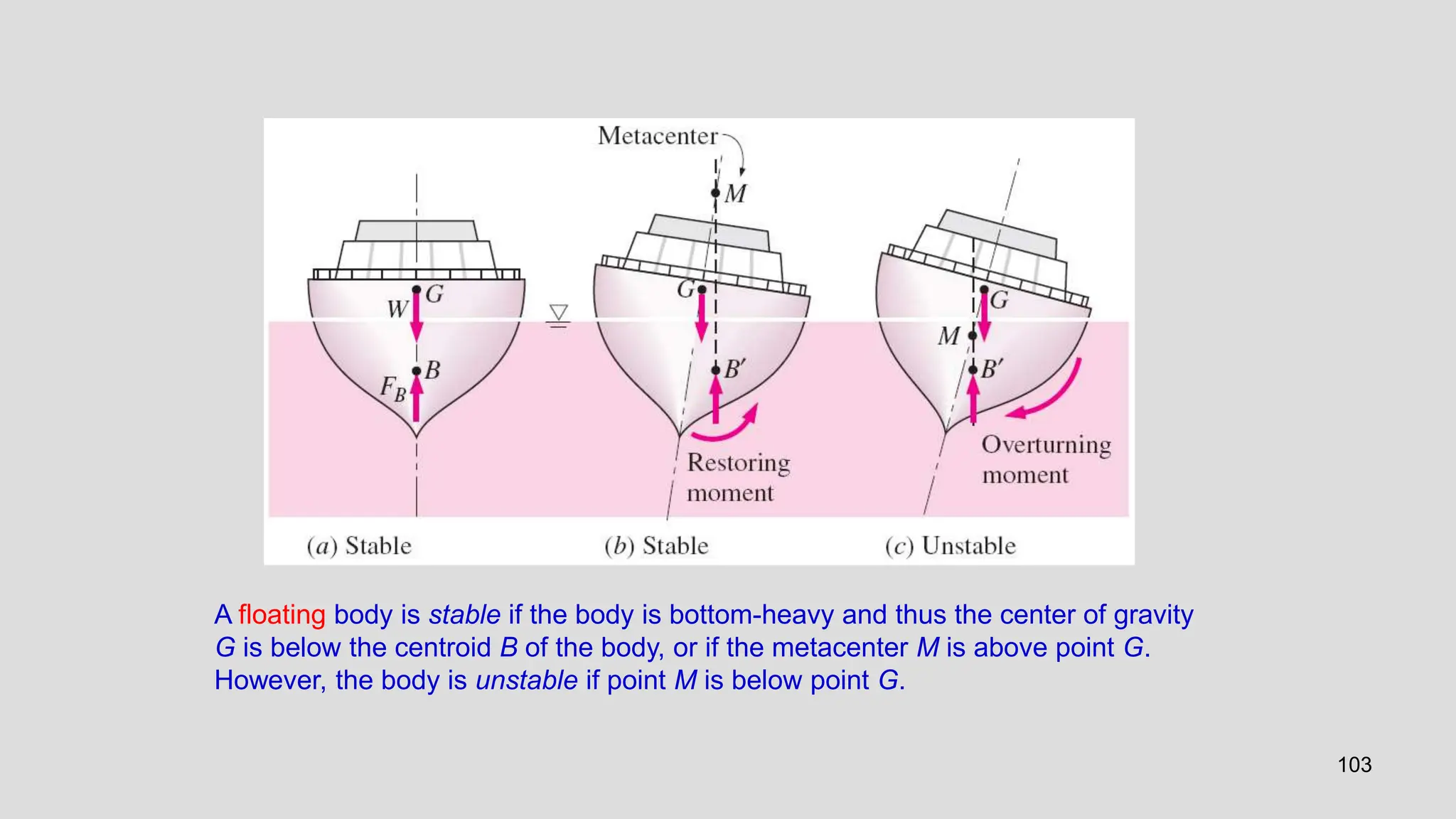
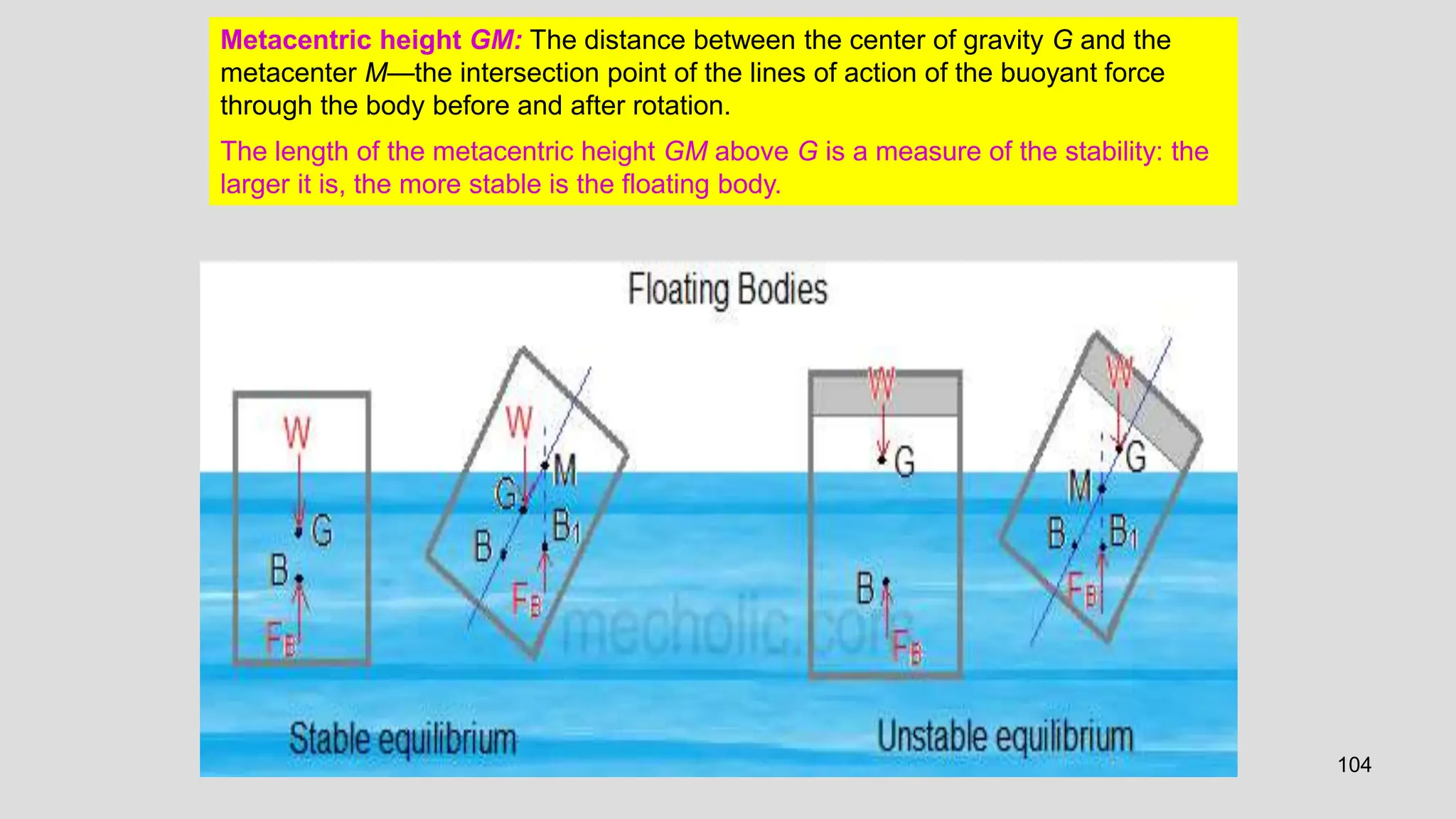
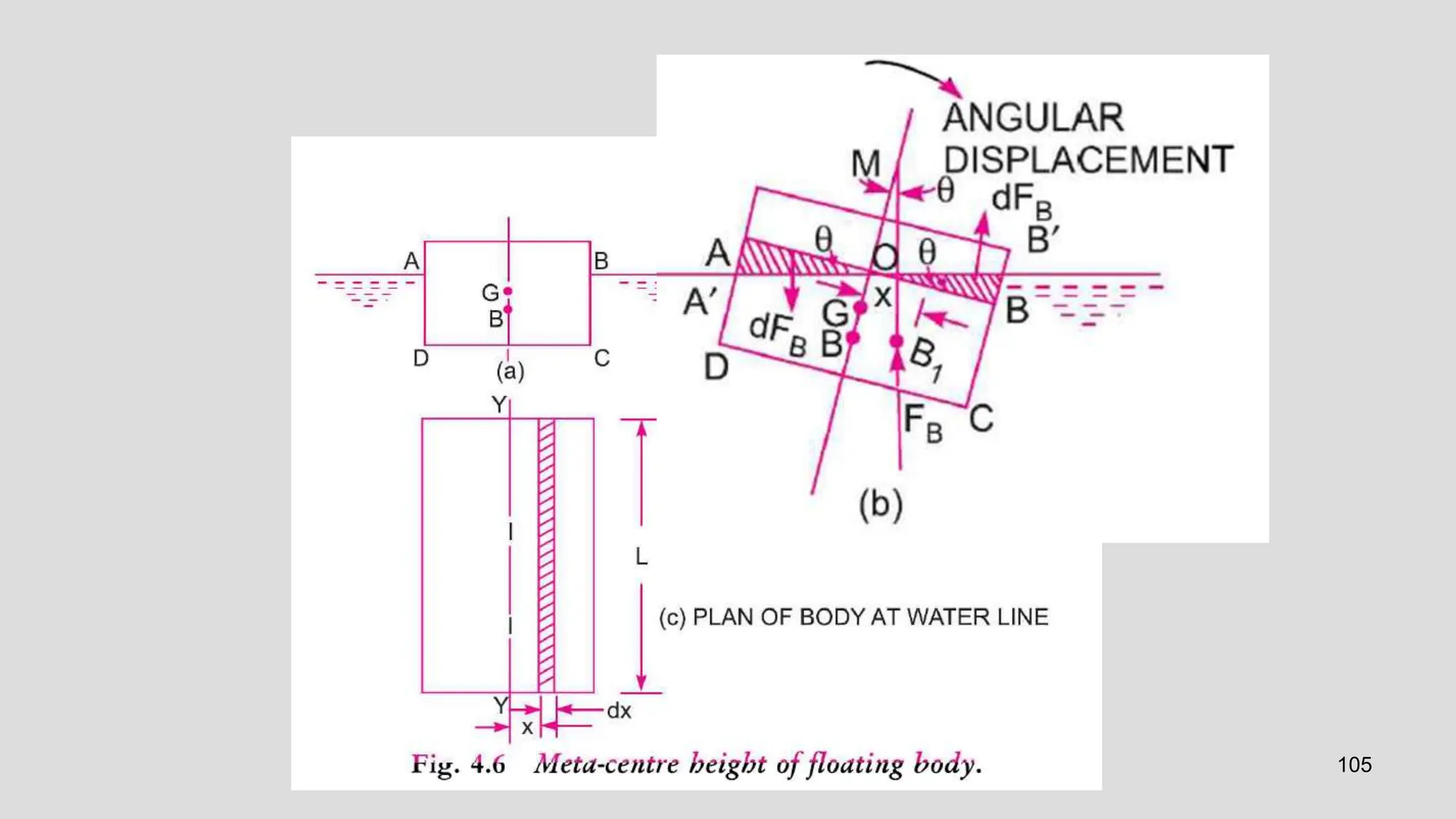
This document covers the properties of fluids, focusing on fluid statics, pressure measurement, density, viscosity, and surface tension. It discusses intensive vs extensive properties, the continuum assumption, drag force, and fluid behavior under shear stress, detailing Newtonian and non-Newtonian fluids. Additionally, it explains buoyancy, Archimedes' principle, hydrostatic forces on submerged surfaces, and stability analysis of floating bodies.

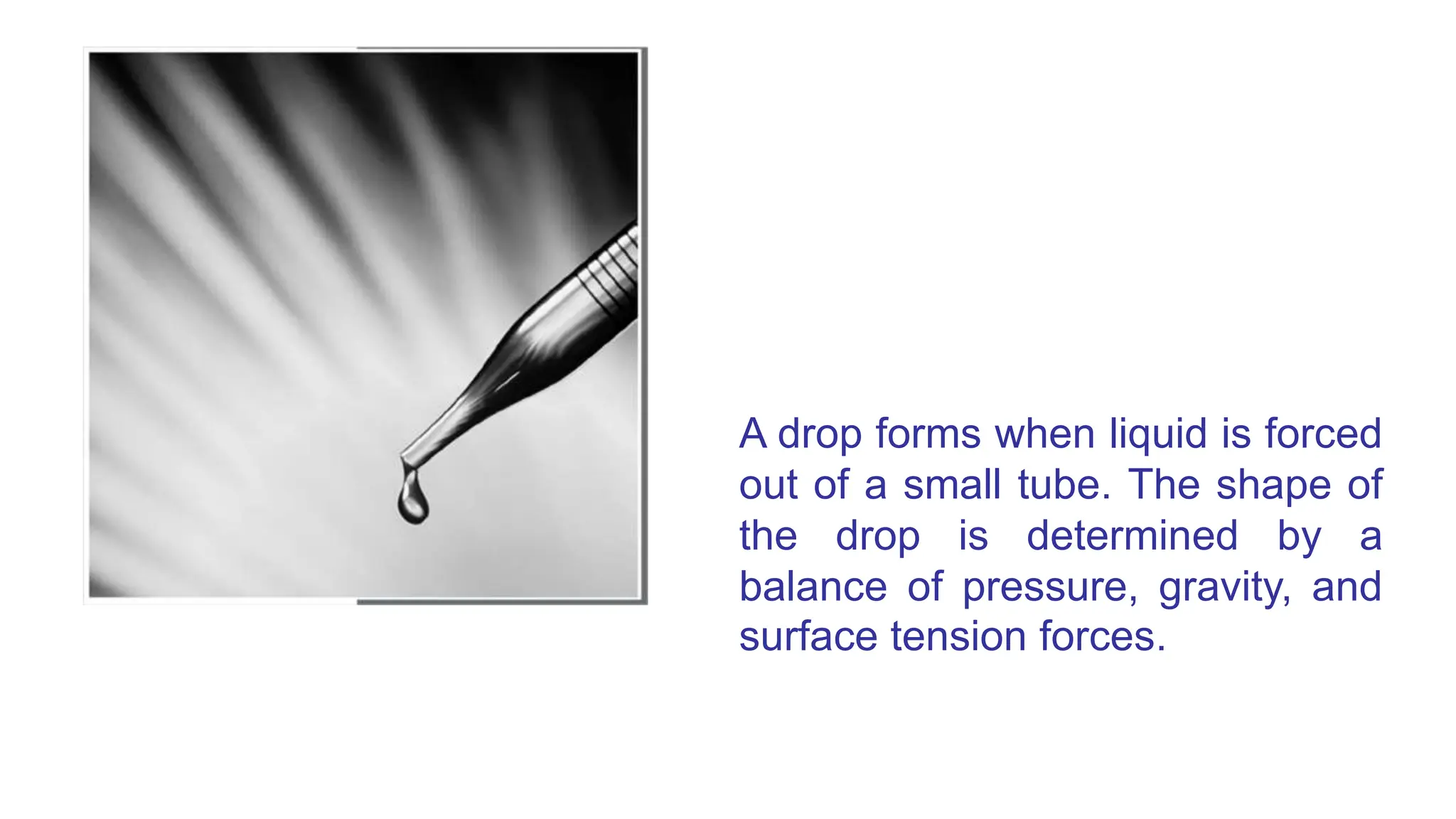











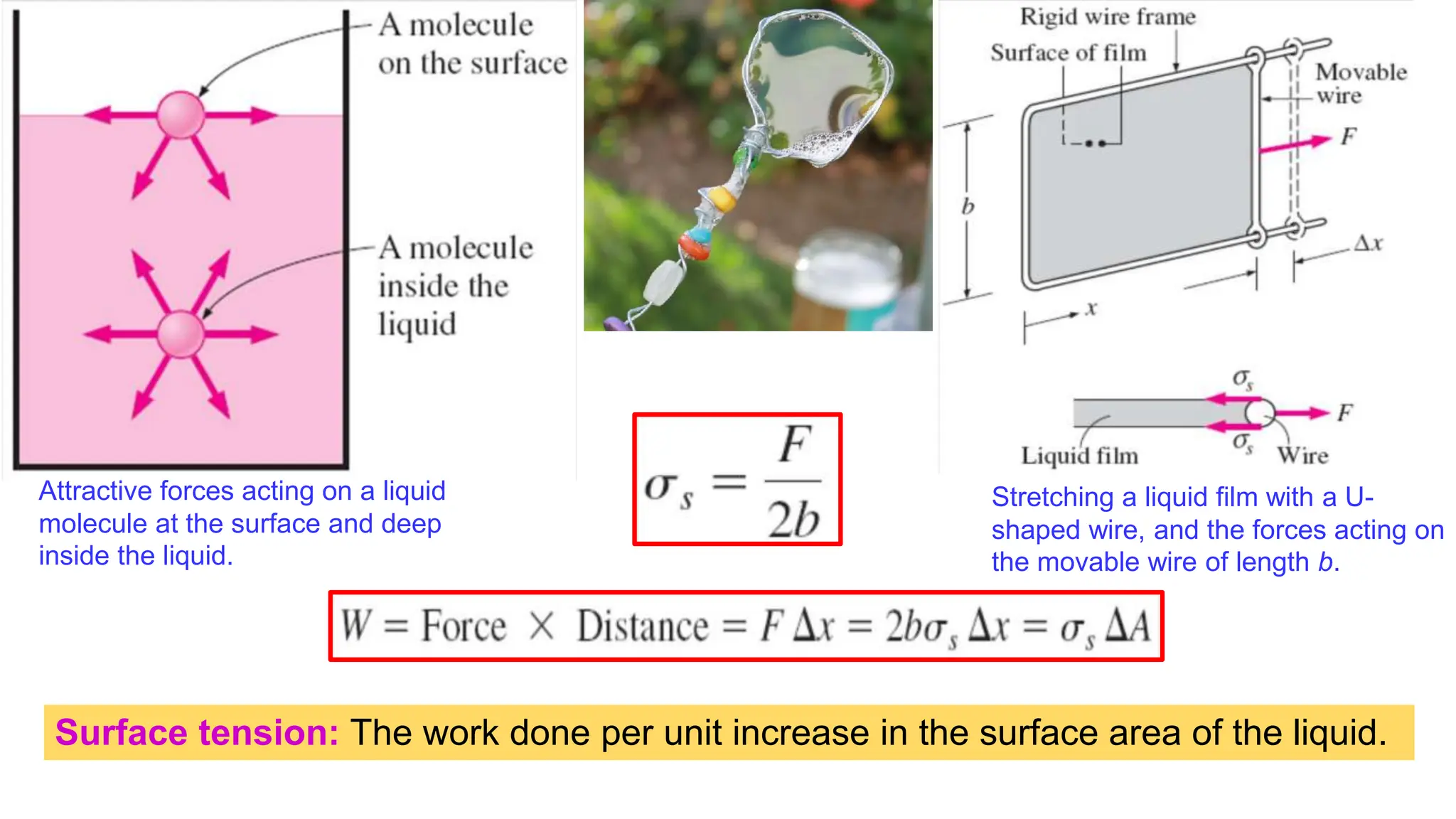
![SURFACE TENSION
• Liquid droplets behave like small balloons filled
with the liquid on a solid surface, and the surface
of the liquid acts like a stretched elastic
membrane under tension.
• The pulling force that causes this tension acts
parallel to the surface and is due to the attractive
forces between the molecules of the liquid.
• The magnitude of this force per unit length is
called surface tension (or coefficient of surface
tension) and is usually expressed in the unit N/m.
• This effect is also called surface energy [per unit
area] and is expressed in the equivalent unit of
N.m/m2.](https://image.slidesharecdn.com/unit1fm-240617160839-927f971f/75/Properties-of-Fluids-Fluid-Statics-Pressure-Measurement-19-2048.jpg)














































![108
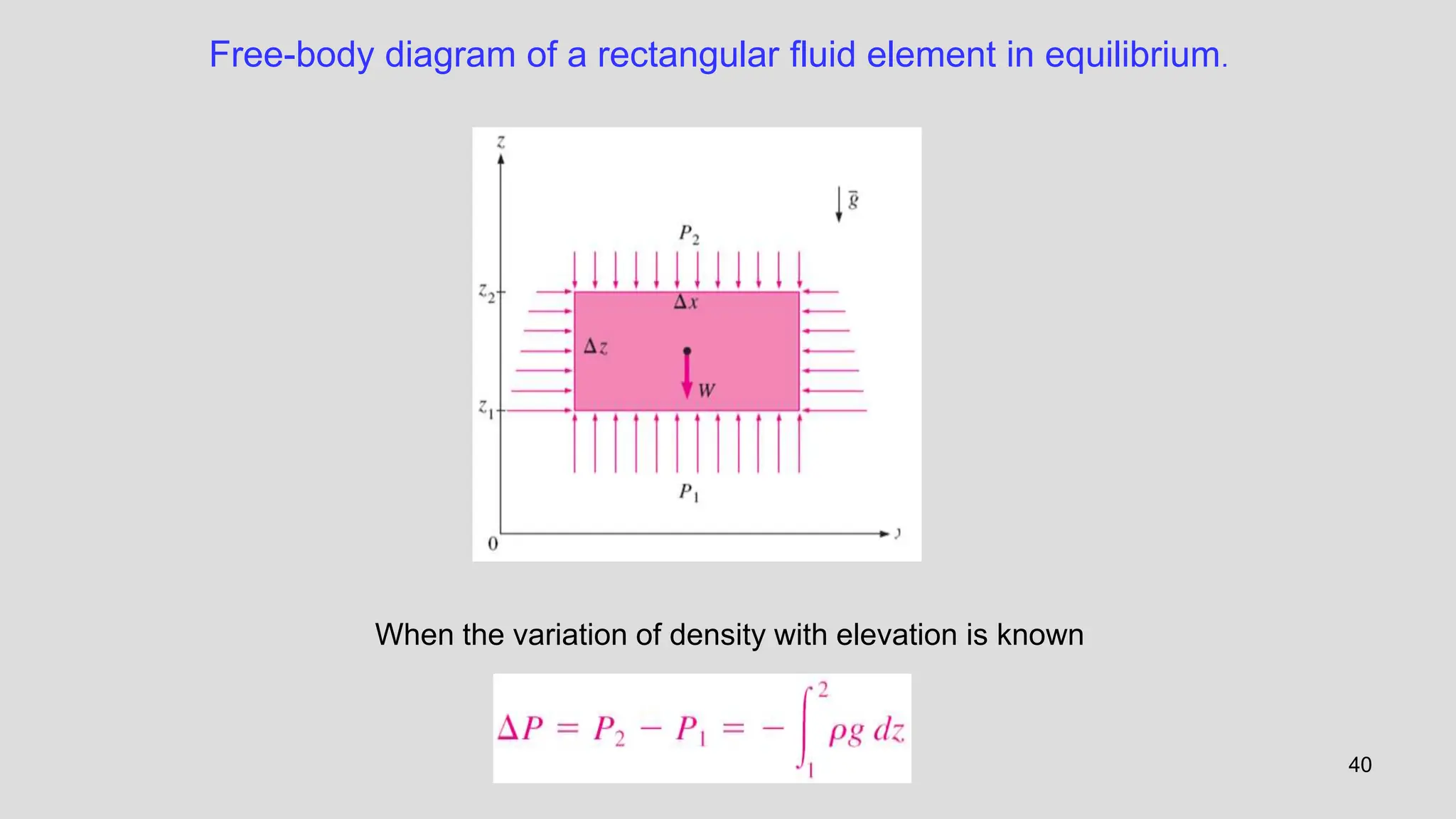
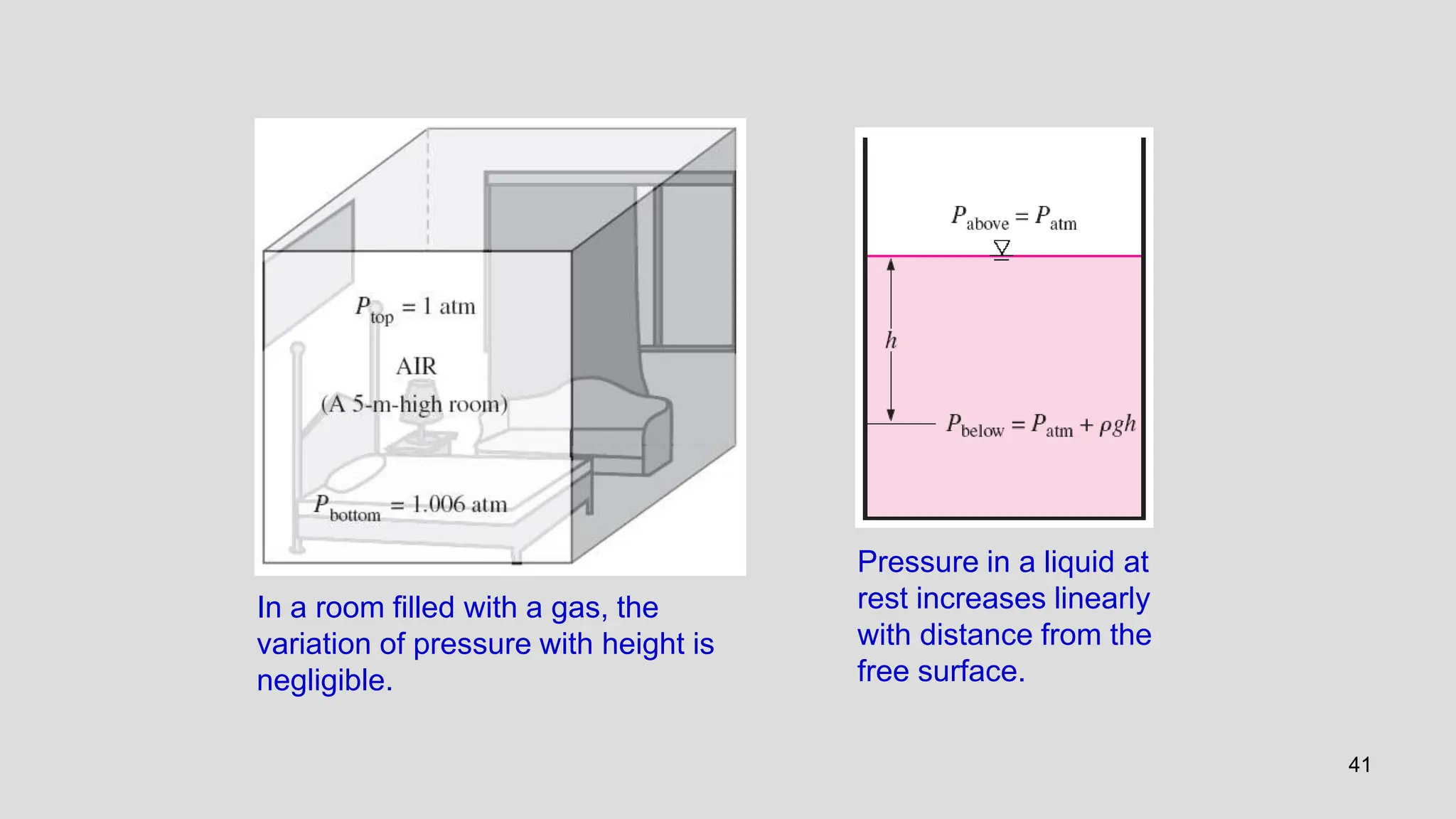
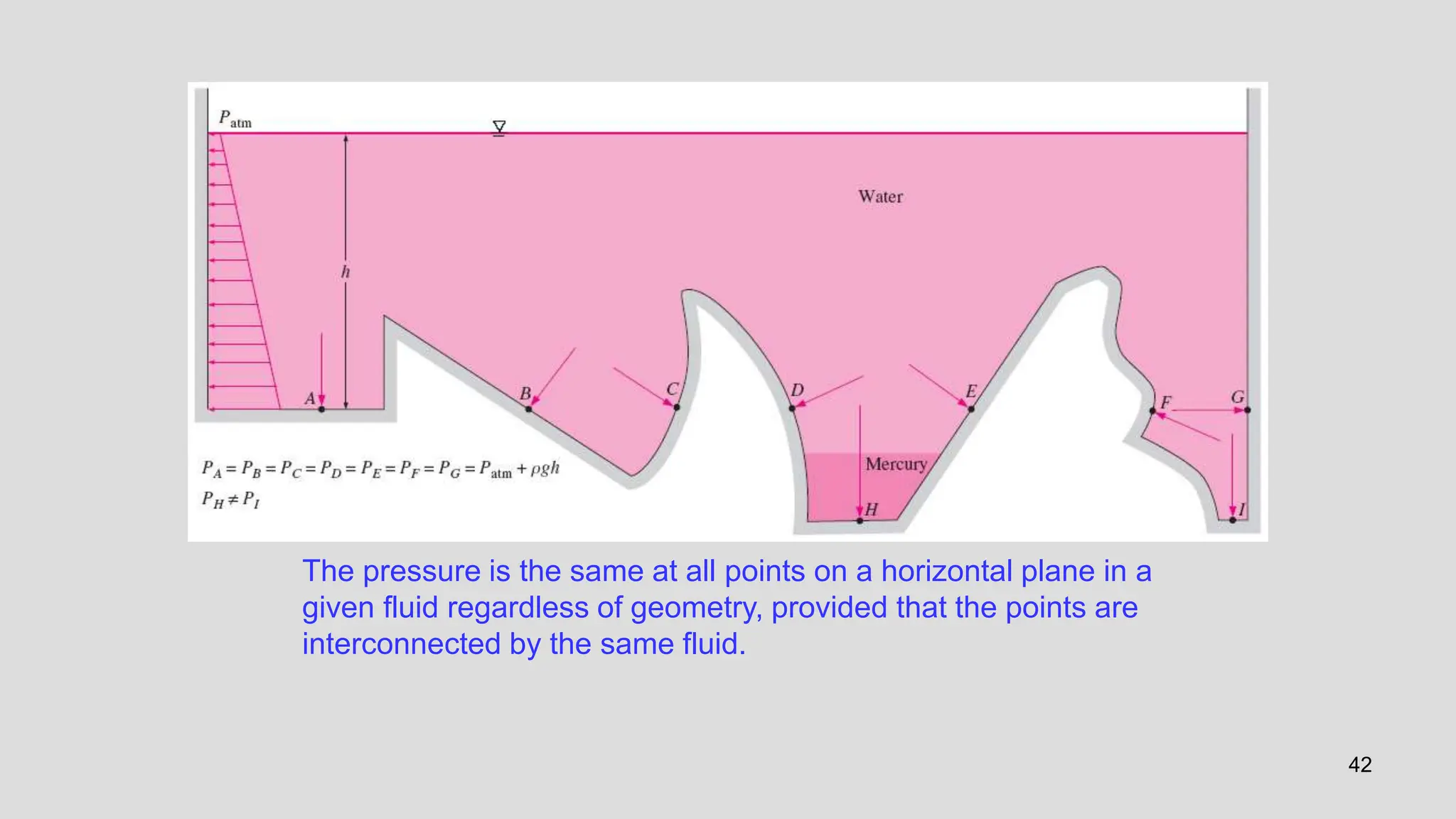
Special Case 1: Fluids at Rest
For fluids at rest or moving on a straight path at constant velocity, all
components of acceleration are zero, and the relations reduce to
The pressure remains constant in any horizontal direction (P is
independent of x and y) and varies only in the vertical direction as
a result of gravity [and thus P = P(z)]. These relations are
applicable for both compressible and incompressible fluids.](https://image.slidesharecdn.com/unit1fm-240617160839-927f971f/75/Properties-of-Fluids-Fluid-Statics-Pressure-Measurement-92-2048.jpg)