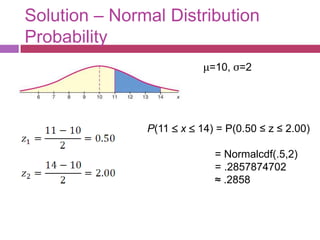
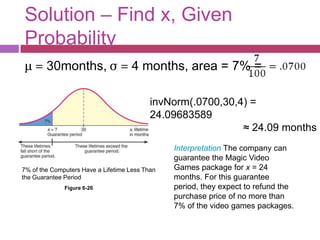
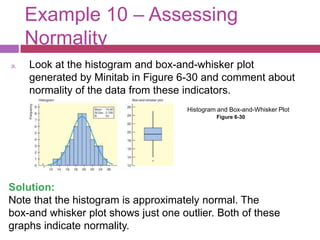
The document discusses how to work with normal distributions when the variable is not standardized. It provides examples of finding probabilities and inverse probabilities for both standardized and unstandardized normal distributions. It also discusses how to assess whether a data set comes from a normal distribution based on the shape of the histogram and presence of outliers.

1. 6.3 AREA UNDER ANY
NORMAL CURVE
Chapter 6:
Normal Curves and Sampling Distributions

2. Page
276
Normal Distribution Areas
 In many applied situations, the original normal
curve is not the standard normal curve.
 How to Work with Normal Distributions
 To find areas and probabilities for a random
variable x that follows a normal distribution with a
mean μ and standard deviation σ, convert x
values to z values using the formula
Then use Table 5 (or calculator) to find
corresponding areas and probabilities.

3. Page
Example 7 – Normal Distribution 277
Probability
Let x have a normal distribution with  = 10
and
 = 2. Find the probability that an x value
selected at random from this distribution is
between 11 and 14. In symbols, find P(11  x 
14).

4. Solution – Normal Distribution
Probability
μ=10, σ=2
P(11  x  14) = P(0.50 ≤ z ≤ 2.00)
= Normalcdf(.5,2)
= .2857874702
≈ .2858

5. Using the Calculator
(without converting to z scores)
Normalcdf (lower bound, upper bound, μ , σ)
-E99 and E99 are used for left tail and right tail
bounds

6. Page
279
Inverse Normal Distribution
 The inverse normal probability distribution
is used when we need to find z or x values that
correspond to a given area under the curve.
 When using Table 5:
Locate the area in the body of the table
 If an exact area is not in the table, use the nearest area
rather than using between values.
 The area you use will depend on which case you have

7. Page
Different Cases of Inverse Normal 279
Distributions
 Left Tail Case: A
Use the shaded area, A
 Right Tail Case:
Use 1 – A (non shaded area) 1–A
 Center Case:
Use the left tail

8. Using the Calculator
 To find x:
 Hit2nd VARS, choose 3:invNorm
 Enter area, μ, σ) ENTER
 To find z:
 Hit2nd VARS, choose 3:invNorm
 Enter area) ENTER
Note: The “area” you use depends on which case
you have!

9. Page
Example 8 – Find x, Given 279
Probability
 Magic Video Games, Inc., sells an expensive
video games package. Because the package is so
expensive, the company wants to advertise an
impressive guarantee for the life expectancy of its
computer control system. The guarantee policy
will refund the full purchase price if the computer
fails during the guarantee period. The research
department has done tests that show that the
mean life for the computer is 30 months, with
standard deviation of 4 months. The computer life
is normally distributed. How long can the
guarantee period be if management does not
want to refund the purchase price on more than
7% of the Magic Video packages?

10. Solution – Find x, Given
Probability
μ = 30months, σ = 4 months, area = 7% =
invNorm(.0700,30,4) =
24.09683589
≈ 24.09 months
Interpretation The company can
guarantee the Magic Video
7% of the Computers Have a Lifetime Less Than Games package for x = 24
the Guarantee Period months. For this guarantee
Figure 6-26 period, they expect to refund the
purchase price of no more than
7% of the video games packages.

11. Page
Example 9 – Find z 281
Find the z value such that 90% of the area
under the standard normal curve lies between
–z and z.
.05
.90
invNorm(.05) = -1.644853626
z = ±1.65

12. Page
How to Determine Whether Data 283
Have a Normal Distribution
 If you are not told in some why that a data set
is normal or approximately normal, then you
need to determine this
 The following guidelines represent useful
devices for determining whether or not data
follow a normal distribution.
1. Histogram: should be roughly bell-shaped
2. Outliers: there should not be more than 1

13. Example 10 – Assessing Page
283
Normality
 Consider the following data, which are
rounded to the nearest integer.

14. Example 10 – Assessing
Normality
a. Look at the histogram and box-and-whisker plot
generated by Minitab in Figure 6-30 and comment about
normality of the data from these indicators.
Histogram and Box-and-Whisker Plot
Figure 6-30
Solution:
Note that the histogram is approximately normal. The
box-and whisker plot shows just one outlier. Both of these
graphs indicate normality.

15. Assignment
 Page 286
 #1 – 3, 4a, 5, 11, 13,15, 19, 23, 27, 29