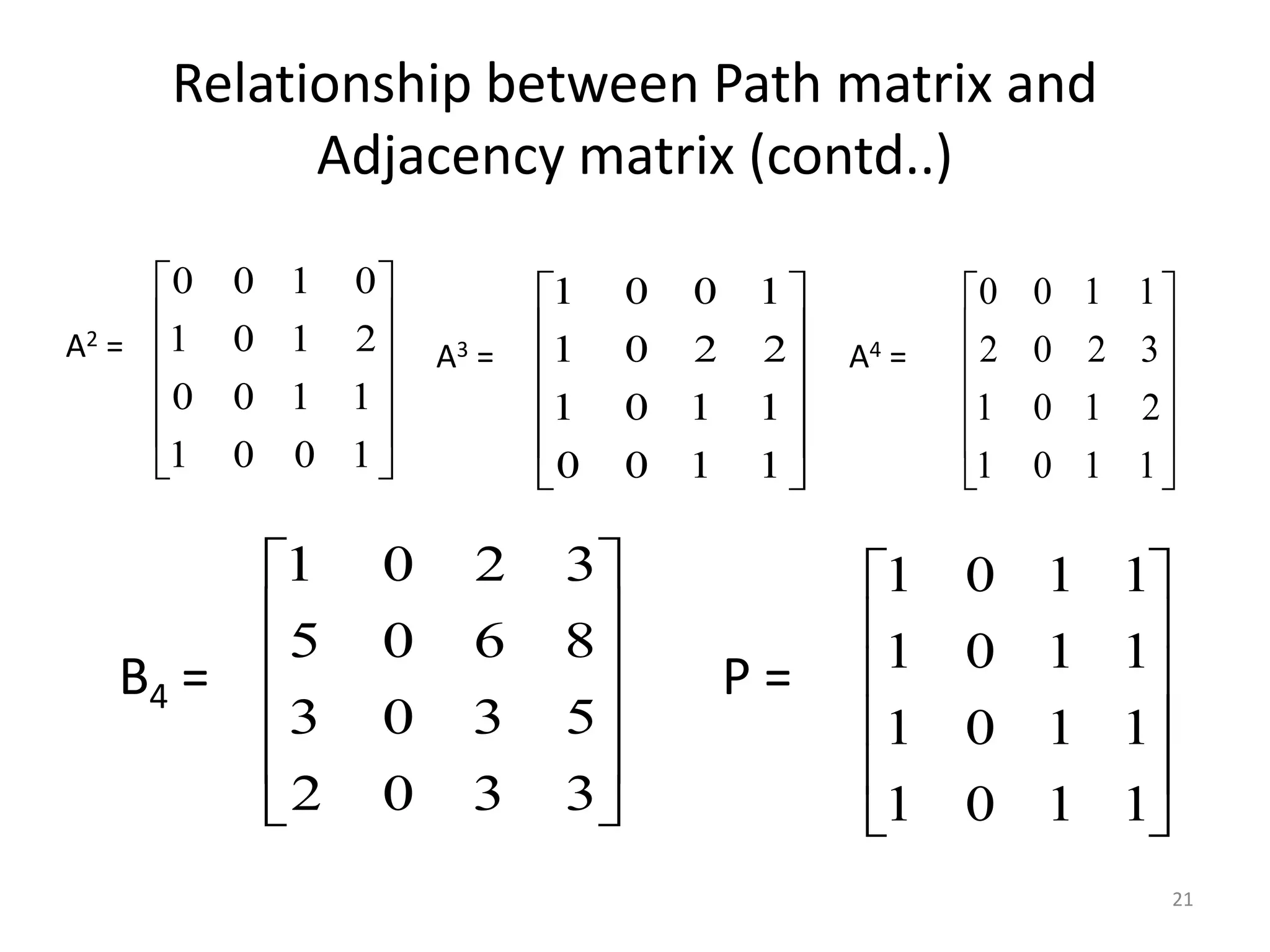
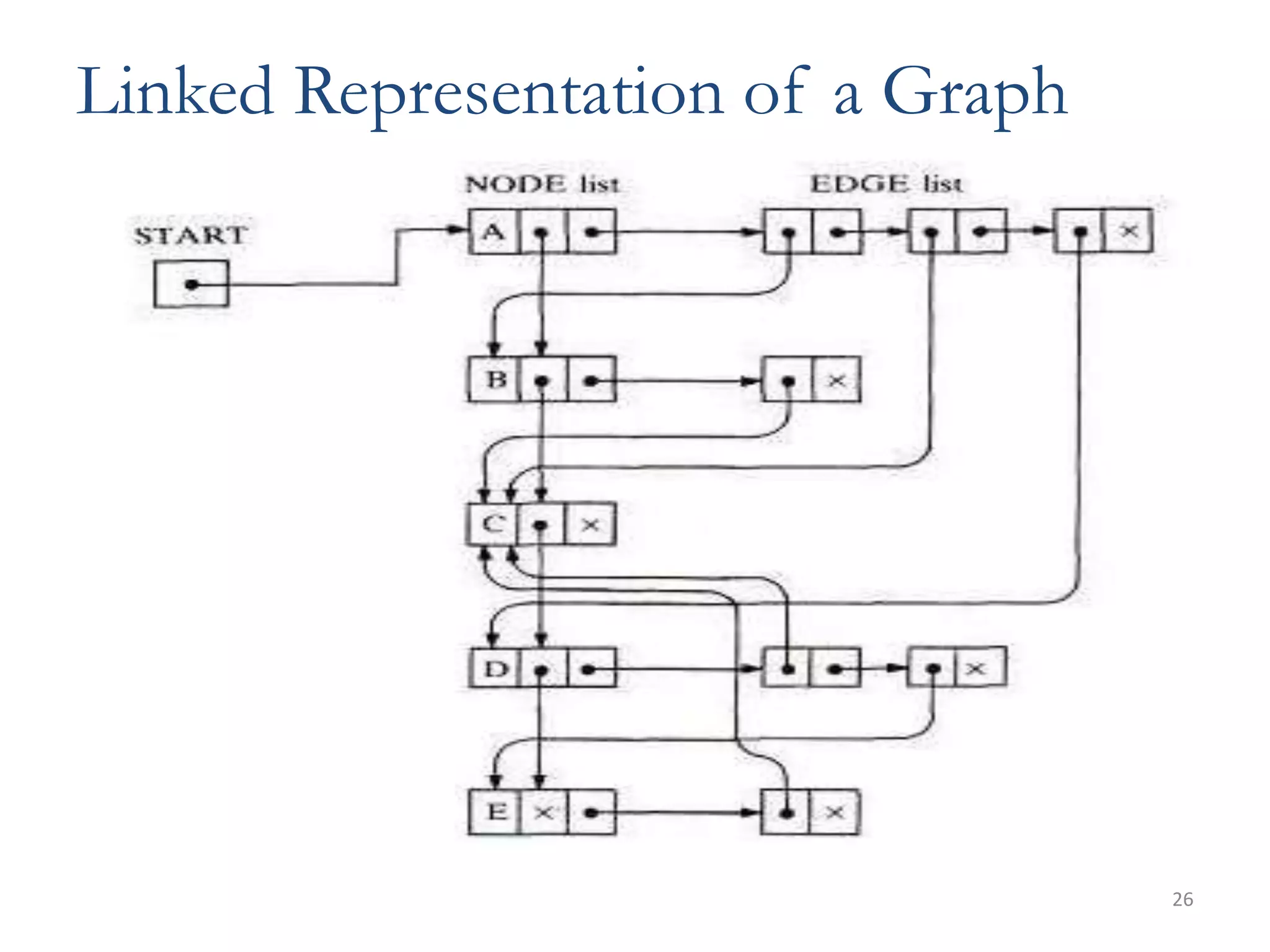
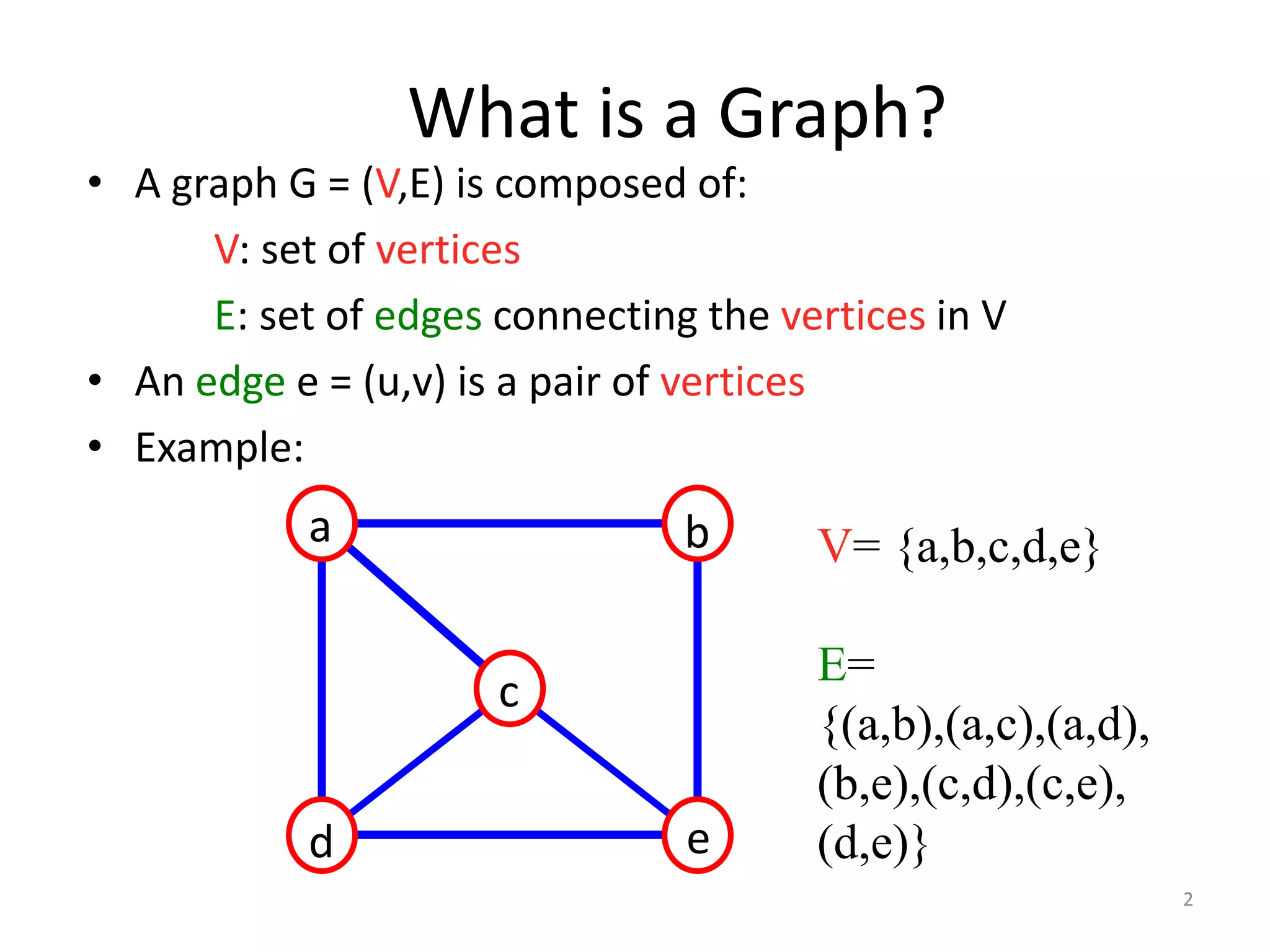
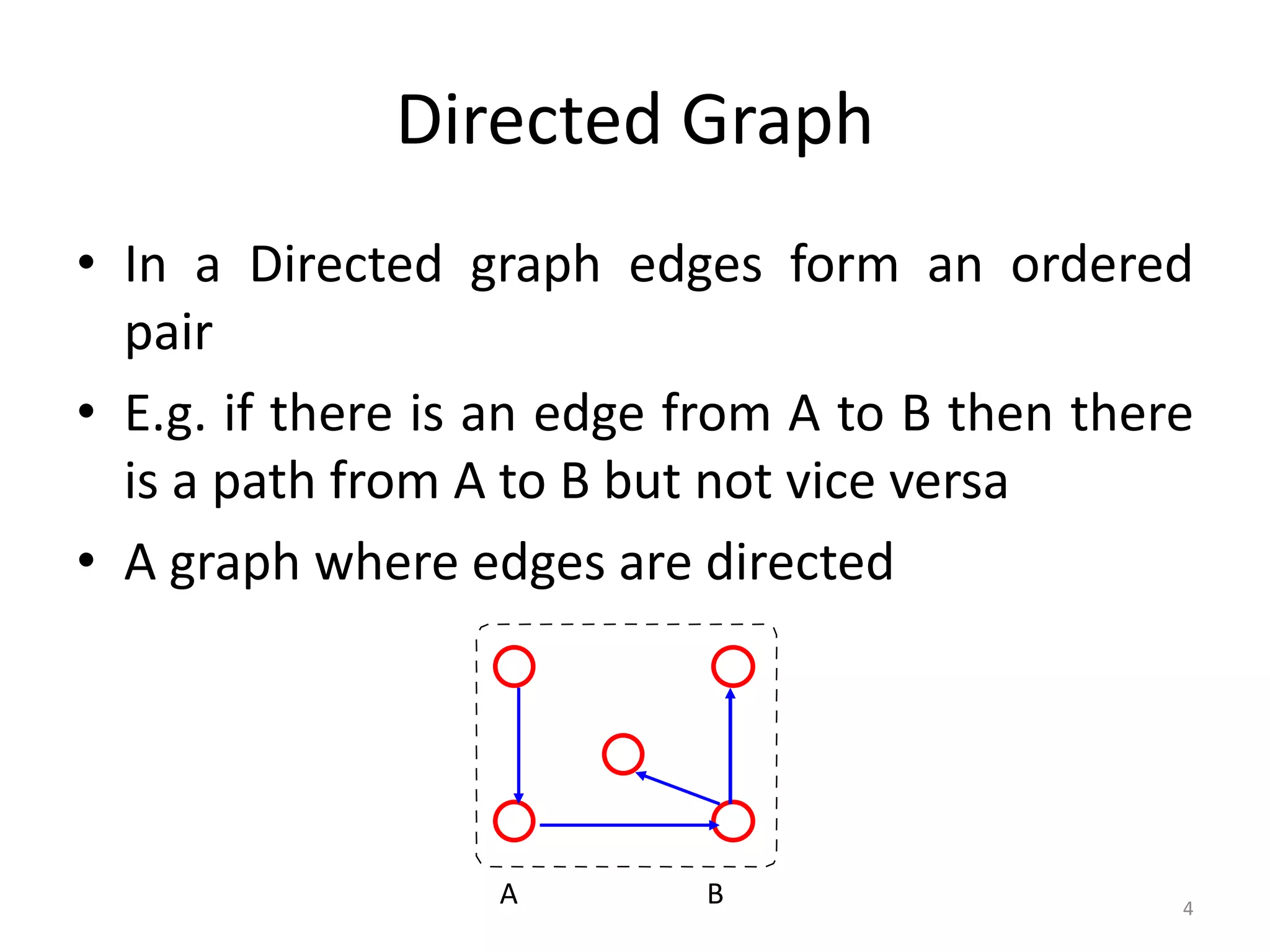
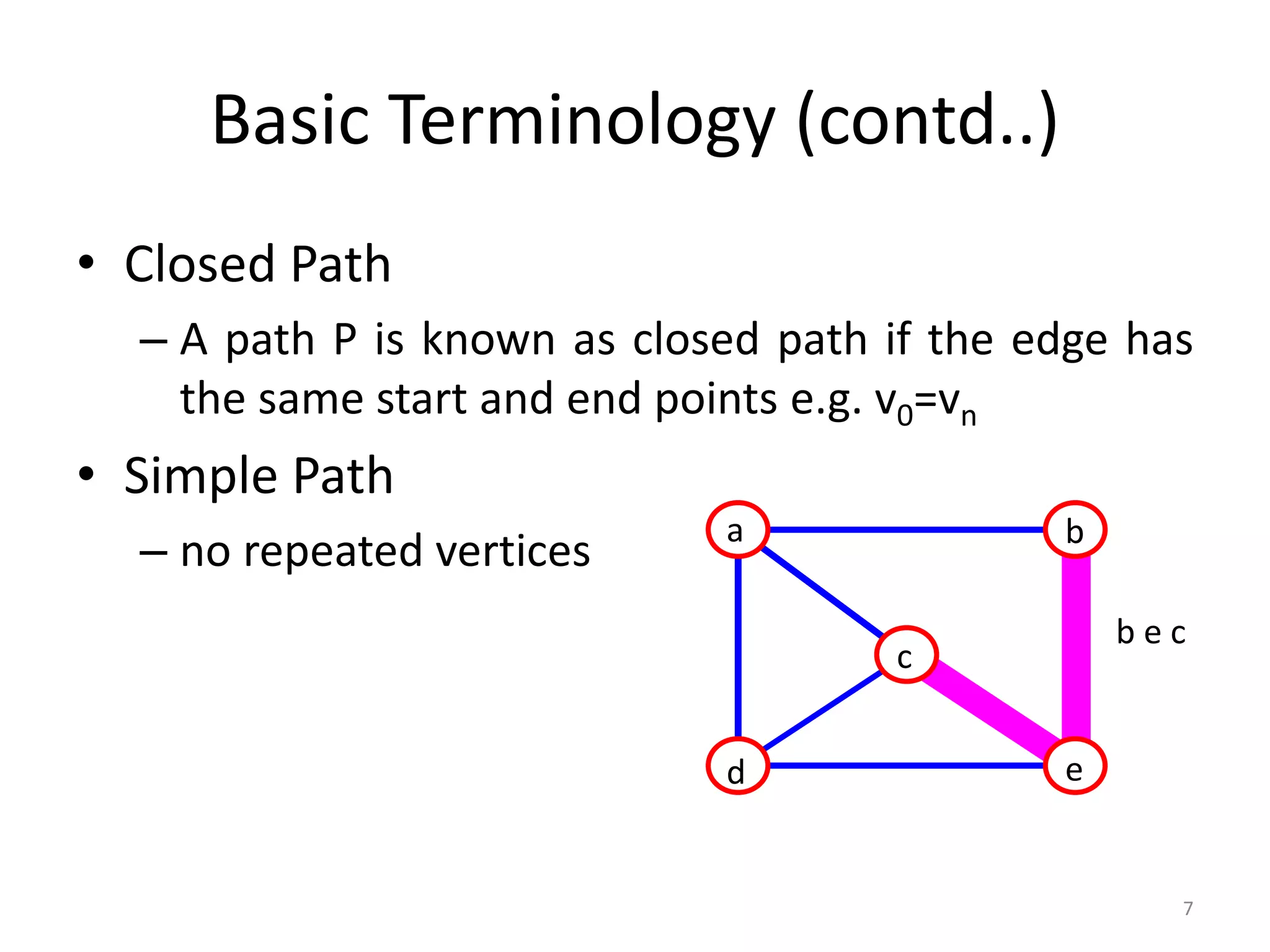
The document defines and explains basic graph terminology and representations. It begins by defining what a graph is composed of, including vertices and edges. It then discusses directed vs undirected graphs and provides examples. It also covers basic graph terminology such as adjacent nodes, degree, paths, cycles, and more. Finally, it discusses different ways of representing graphs, including adjacency matrices, adjacency lists, and traversing graphs using breadth-first and depth-first search algorithms.

1. 1
Graphs

2. 2
What is a Graph?
• A graph G = (V,E) is composed of:
V: set of vertices
E: set of edges connecting the vertices in V
• An edge e = (u,v) is a pair of vertices
• Example:
a b
c
d e
V= {a,b,c,d,e}
E=
{(a,b),(a,c),(a,d),
(b,e),(c,d),(c,e),
(d,e)}

3. 3
• A graph can be Directed or Undirected
• In an undirected graph, the edges do not have
any direction associated with them
• E.g. if there is an edge between A and B then
the nodes can be traversed from A to B as well
as from B to A
• The graph shown in the previous slide is
undirected

4. 4
Directed Graph
• In a Directed graph edges form an ordered
pair
• E.g. if there is an edge from A to B then there
is a path from A to B but not vice versa
• A graph where edges are directed
A B

5. 5
Basic Terminology
• Adjacent Nodes
– If (v0, v1) is an edge in an undirected graph, then v0
and v1 are Adjacent or Neighbours
– If <v0, v1> is an edge in a directed graph, then v0 is
adjacent to v1, and v1 is adjacent from v0
• Degree of a node
– The degree of a vertex is
the total number of edges
containing the vertex
– If a vertex has degree 0,
then it means it is an
Isolated node
3
3 3
3
2

6. 6
Basic Terminology (contd..)
• Regular Graph
– It is a graph where each vertex has the same
number of neighbours
– i.e. Every node has a same degree
– A regular graph with vertices of degree k is called
k-regular graph
• Path
– sequence of vertices v1,v2,. . .vk
such that consecutive vertices
vi and vi+1 are adjacent.
a b
c
d e
b e d c

7. 7
Basic Terminology (contd..)
• Closed Path
– A path P is known as closed path if the edge has
the same start and end points e.g. v0=vn
• Simple Path
– no repeated vertices a b
c
d e
b e c

8. 8
Basic Terminology (contd..)
• Cycle
– A Closed Simple path,
with length 3 or more
• Connected graph
– Any two vertices are connected by some path
a
a b
c
d e
connected not connected

9. 9
Basic Terminology (contd..)
• Complete Graph
– A Graph G is said to be complete if all its nodes are
fully connected
– A complete Graph has n(n-1)/2 edges, where n is the
number of nodes in G
• Labeled / Weighted Graph
– Every edge in the Graph is
assigned some data
– The edges of the Graph
are assigned some weight
or length

10. 10
Basic Terminology (contd..)
• Multiple Edges
– Distinct edges which connect the same end points
are called multiple edges
• Loop
– An edge that has Identical end points
• Multigraph
– With multiple edges and / or
a loop is called Multigraph
• Size of a Graph
– Total number of edges in G

11. 11
Directed Graph
• In a Directed graph edges form an ordered
pair (u, v) of nodes in G
• The edge begins at u and terminates at v
• u as the origin point of e and v as the
destination point of e
• u is the predecessor of v and v is the successor
of u

12. 12
Terminology of a Directed Graph
• Out degree of a node
– Total number of edges that originate at a node
• In degree of a node
– Total number of edges that terminate at a node
• Degree of a node
– Sum of In-degree and Out-degree
• Source
– If it has a positive out-degree but a zero in-degree
• Sink
– If it has a positive in-degree but a zero out-degree

13. 13
Directed Graph
0
1
2
G
in:1, out: 1
in: 1, out: 2
in: 1, out: 0
s: Source
t: Sink

14. 14
Graph Representations
• Adjacency Matrix
• Path Matrix
• Adjacency Lists

15. 15
Adjacency Matrix
• Let G=(V,E) be a graph with n vertices.
• The adjacency matrix of G is a two-dimensional
n by n array, say adj_mat
• If the edge (vi, vj ) is in E(G), adj_mat[i][j]=1
• If there is no such edge in E(G), adj_mat[i][j]=0
• The adjacency matrix for an undirected graph is
symmetric
• The adjacency matrix for a digraph
need not be symmetric

16. 16
Examples for Adjacency Matrix












0
1
1
1
1
0
1
1
1
1
0
1
1
1
1
0 0
1
0
1
0
0
0
1
0










0
1
1
0
0
0
0
0
1
0
0
1
0
0
0
0
1
0
0
1
0
0
0
0
0
1
1
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
1
0
1
0
0
0
0
0
0
1
0
1
0
0
0
0
0
0
1
0


























G1
G2
G4
0
1 2
3
0
1
2
1
0
2
3
4
5
6
7
symmetric

17. 17
Merits of Adjacency Matrix
 From the adjacency matrix, to determine the
connection of vertices is easy
 The degree of a vertex is
 For a digraph (= directed graph), the row sum is
the out_degree, while the column sum is the
in_degree
adj mat i j
j
n
_ [ ][ ]


0
1
ind vi A j i
j
n
( ) [ , ]



0
1
outd vi A i j
j
n
( ) [ , ]



0
1

18. 18
Path Matrix
• Let G be a simple directed graph with m nodes, v1,v2,. .
.vm The path matrix or reachability matrix of G is the m-
square matrix P=(Pij) defined as follows:
Pij =1 if there is a path from vi to vj
= 0 Otherwise
• Suppose there is a path from vi to vj. Then there must be
a simple path from vi to vj when vi != vj or there must be a
cycle from vi to vj when vi = vj.
• Since G has only m nodes, such a simple path must have
length m-1 or less, or such a cycle must have length m or
less

19. 19
Relationship between Path matrix and
Adjacency matrix
• Let A be the adjacency matrix of a graph G. Then Ak(i,j),
the ij entry in the matrix Ak, gives the number of paths of
length K from vi to vj.
• Likewise, we can calculate A2, A3, A4 ,……
• Let A be the adjacency matrix and let P=(Pij) be the Path
matrix of a digraph G. Then Pij= 1 if and only if there is a
nonzero number in the ij entry of the matrix
Bm = A + A2 + A3+……….+ Am
• The main goal to define matrix B is to obtain the Path
matrix P. P can be obtain by replacing the non-zero
entries in B by 1.

20. 20
Relationship between Path matrix and
Adjacency matrix (contd..)
Y X
WZ












0
1
1
1
1
0
1
0
0
0
0
0
0
1
1
0
A =
Here, v1 = X, v2 = Y, v3 = Z, v4 = W

21. 21
Relationship between Path matrix and
Adjacency matrix (contd..)












1
2
3
1
1
1
2
1
0
0
0
0
1
1
2
0












3
5
8
3
3
3
6
2
0
0
0
0
2
3
5
1












1
1
1
1
1
1
1
1
0
0
0
0
1
1
1
1












1
1
2
1
1
1
2
0
0
0
0
0
0
1
1
1
A2 = A3 = A4 =
B4 = P =












1
1
2
0
0
1
1
1
0
0
0
0
1
0
1
0

22. 22
Linked Representation of a Graph
• The sequential representation of G in memory
i.e. the representation of G by its adjacency
matrix A – has a number of major drawbacks.
• First of all, it may be difficult to insert and
delete nodes in G.
• Size of A may need to be changed and the
nodes may need to be recorded.
22

23. 23
0
1
2
3
0
1
2
0
1
2
3
4
5
6
7
1 2 3
0 2 3
0 1 3
0 1 2
G1
1
0 2
G3
1 2
0 3
0 3
1 2
5
4 6
5 7
6
G4
0
1 2
3
0
1
2
1
0
2
3
4
5
6
7
An undirected graph with n vertices and e edges ==> n head nodes and 2e list nodes
Adjacency
Lists

24. 24
Example

25. 25
NODE NEXT ADJ Other Information (e.g. indeg,
outdeg, status)
Node Structure
DEST LINK Other Information (e.g. weight)
Edge Structure

26. 26
Linked Representation of a Graph

27. 27
Graph Traversals
1. Breadth First Search
2. Depth First Search

28. 28
Algorithm for Breadth First Search
1. Initialize all nodes to the ready State (STATUS=1)
2. Put the starting node A in QUEUE and change its status to
the waiting state (STATUS=2)
3. Repeat Steps 4 & 5 until QUEUE is empty :
4. Remove the front node N of QUEUE. Process N and
change the status of N to the processed state (STATUS=3)
5. Add to the rear of QUEUE all the neighbours of N that are
in the ready state (STATUS=1) and change their status to
the waiting state (STATUS=2)
6. Exit
28

29. 29
Example for Breadth First Search
The Adjacent List is
11 -> 12,18,13
12-> 11,14,15
13-> 11,16,17
14-> 12,18
15-> 12,18
16-> 13,18
17-> 13,18
18-> 14,15,11,16,17

30. 30
Description of Example
• Let us suppose that starting node is 11, The steps to
traverse graph using Breadth First Search Is
• Step 1: Add 11 to queue
Front: 1 Queue: 11
Rear:1
• Step 2: Delete element at Front position (11) and add all
the adjacent nodes of deleted node that are not visited.
Front: 2 Queue: X,12, 18, 13
Rear:4

31. 31
• Step 3: Delete element at Front position (12) and add all
the adjacent nodes of deleted node that are not visited.
Front: 3 Queue: X,X,18, 13, 14, 15
Rear:6
11 already visited; i.e. in Queue or deleted
• Step 4: Delete element at Front position (18) and add all
the adjacent nodes of deleted node that are not visited.
Front: 4 Queue: X,X,X,13, 14, 15, 16,17
Rear:8
11,14,15 already visited; i.e. in Queue or deleted

32. 32
• Step 5: Delete element at Front position (13) and add all
the adjacent nodes of deleted node that are not visited.
Front: 5 Queue: X,X,X,X, 14, 15, 16,17
Rear:8
No vertex added because 11,16,17 already visited; i.e. in
Queue or deleted
• Step 6: Delete element at Front position (14) and add all
the adjacent nodes of deleted node that are not visited.
Front: 6 Queue: X,X,X,X, X, 15, 16,17
Rear:8
No vertex added because 12 and 18 already visited; i.e. in
Queue or deleted

33. 33
• Step 7: Delete element at Front position (15) and add all
the adjacent nodes of deleted node that are not visited.
Front: 7 Queue: X,X,X,X, X,X,16,17
Rear:8
No vertex added because 12 and 18 already visited; i.e. in
Queue or deleted
• Step 8: Delete element at Front position (16) and add all
the adjacent nodes of deleted node that are not visited.
Front: 8 Queue: X,X,X,X, X,X,X,17
Rear:8
No vertex added because 13 and 18 already visited; i.e. in
Queue or deleted

34. 34
• Step 9: Delete element at Front position (17) and add all
the adjacent nodes of deleted node that are not visited.
Front: 8 Queue: X,X,X,X, X,X,X,X
Rear:8
No vertex added because 13 and 18 already visited; i.e. in
Queue or deleted
Queue EMPTY. Therefore Breadth First Search is
11,12,18,13,14,15,16,17

35. 35
Algorithm for Depth First Search
1. Initialize all nodes to the ready State (STATUS=1)
2. Put the starting node A onto STACK and change its
status to the waiting state (STATUS=2)
3. Repeat Steps 4 & 5 until STACK is empty :
4. POP the top node N of STACK. Process N and change the
status of N to the processed state (STATUS=3)
5. PUSH onto STACK all the neighbours of N that are in the
ready state (STATUS=1) and change their status to the
waiting state (STATUS=2)
6. Exit
35

36. 36
Example for Depth First Search
The Adjacent List is
11 -> 12,18,13
12-> 11,14,15
13-> 11,16,17
14-> 12,18
15-> 12,18
16-> 13,18
17-> 13,18
18-> 14,15,11,16,17

37. 37
Description of Example
• Let us suppose that starting node is 11, The steps to
traverse graph using Depth First Search is
• Step 1: Push 11 onto the Stack
Stack: 11
• Step 2: Pop the top element i.e. last added (11) from the
stack and push all adjacent vertex of popped vertex onto
the stack that are not visited.
Stack: 12,18,13

38. 38
• Step 3: Pop the top element i.e. last added (13) from the
stack and push all adjacent vertex of popped vertex onto
the stack that are not visited.
Stack: 12,18,16,17
11 not added because already visited; i.e. onto stack or
deleted
• Step 4: Pop the top element i.e. last added (17) from the
stack and push all adjacent vertex of popped vertex onto
the stack that are not visited.
Stack: 12,18,16
13 and 18 not added because already visited; i.e. onto
stack or deleted

39. 39
• Step 5: Pop the top element i.e. last added (16) from the
stack and push all adjacent vertex of popped vertex onto
the stack that are not visited.
Stack: 12,18
13 and 18 not added because already visited; i.e. onto
stack or deleted
• Step 6: Pop the top element i.e. last added (18) from the
stack and push all adjacent vertex of popped vertex onto
the stack that are not visited.
Stack: 12,14,15
11,16 and 17 not added because already visited; i.e. onto
stack or deleted

40. 40
• Step 7: Pop the top element i.e. last added (15) from the
stack and push all adjacent vertex of popped vertex onto
the stack that are not visited.
Stack: 12,14
12 and 18 not added because already visited; i.e. onto
stack or deleted
• Step 8: Pop the top element i.e. last added (14) from the
stack and push all adjacent vertex of popped vertex onto
the stack that are not visited.
Stack: 12
12 and 18 not added because already visited; i.e. onto
stack or deleted

41. 41
• Step 9: Pop the top element i.e. last
added (12) from the stack and push all
adjacent vertex of popped vertex onto the
stack that are not visited.
• Stack: ----
• 11, 14 and 15 not added because already
visited; i.e. onto stack or deleted
• Stack Empty. Therefore the Depth First Search
is 11,13,17,16,18, 15,14,12