1. A queue is a collection of items that are inserted at one end and removed from the other, following a first-in first-out (FIFO) order. Common queue operations are enqueue to insert and dequeue to remove. 2. Queues can be implemented using arrays or linked lists. Array implementation uses a front and rear pointer to track the first and last elements. Linked list implementation uses front and rear pointers to point to the first and last nodes. 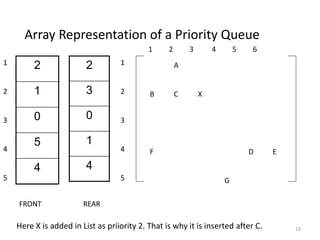3. A priority queue is like a regular queue but allows extracting elements based on priority rather than strictly FIFO order. Higher priority elements are processed before lower priority ones.

1. 1
Queues
• A queue is an ordered collection of items from which items may
be deleted at one end(front) and into which items are inserted at
the other end(rear).
• queue – similar to a supermarket checkout line
– first-in, first-out (FIFO)
– nodes are removed only from the head (front)
– nodes are inserted only at the tail(rear)
• The insert and remove operations are known as enqueue and
dequeue
Useful in computing
– Print spooling, packets in networks, file server requests
Three operations in the queue are
Insert(q,x) x=remove(q) empty(q)

2. 2
Implementation of Queue
• Array implementation
#define MAXQUEUE 100
struct queue{
int items[MAXQUEUE];
int front,rear;
}q;
0
1
2
3
4
q.front=-1
q.rear=-1
q.items
0
1
2
3
4
q.items
A
B
C
q.front=0
q.rear=2
0
1
2
3
4
q.items
C q.front=q.rear=2
Queue is empty whenever q.rear<q.front
The number of elements in a queue is q.rear-q.front+1

3. 3
Insert operation
QINSERT [ QUEUE, MAXSIZE, ITEM]
1. Initialization
Set Front = -1
Set Rear = -1
2. If Rear = = MAXSIZE-1 then Queue Overflow and Return
3. If Front = = -1 then
Front = 0
Rear = 0
Else
Rear = Rear + 1
4. Set Queue [Rear] = Item and Return

4. 4
Delete Operation
QDELETE [ QUEUE, MAXSIZE, ITEM]
1. If Front = = -1 then Queue Underflow and Return
2. Set Item = Queue [ Front]
3. If Front = = Rear then
Set Front = -1
Set Rear = -1
Else
Front = Front + 1
4. Print, Deleted Item is “ITEM” and Return

5. 5
Circular Queue
• A circular queue is one in which the insertion
of a new element is done at the very first
location of the queue if the last location of the
queue is full
• In other words, if we have a queue Q of say n
elements, then after inserting an element last
(i.e. in the n-1th) location of the array the next
element will be inserted at the very first
location (i.e. 0th location) of the array

6. 6

7. 7
Insertion operation in Circular queue
QINSERT [ QUEUE, N, Front, Rear, ITEM]
1. If Front ==0 and Rear == N-1
OR
Front == Rear+1, then Write Overflow queue and Return
2. If Front = = -1 then
Front = 0
Rear = 0
Else if Rear ==N-1 then
Set Rear = 0
Else
Rear = Rear + 1
3. Set Queue [Rear] = Item and Return

8. 8
Deletion operation in circular queue
QDELETE [ QUEUE, N, Front, Rear, ITEM]
1. If Front = = -1 then Queue Underflow and Return
2. Set Item = Queue [ Front]
3. If Front = = Rear then
Set Front = -1
Set Rear = -1
Else if Front ==N-1 then
Set Front = 0
Else
Front = Front + 1
4. Print, Deleted Item is “ITEM” and Return

9. 9
Advantage of Circular Queue over Linear
Queue
• A circular queue overcomes the problem of
unutilized space in linear queue implemented
as arrays.

10. 10
Linked Representation of Queue
• A linked queue is queue implemented as a
linked list with two pointer variables FRONT
and REAR pointing to the nodes which is in the
FRONT and REAR of the queue
• The INFO fields of the list hold the elements of
the queue
• The LINK fields hold pointers to the
neighboring elements in the queue

11. 11
Linked representation of Queue
Front Rear
Q
A B C D
In the case of insertion into a linked queue ,a
node borrowed from AVAIL list and carrying the
item is to be inserted added as the last node in
the linked representation of queue.

12. 12
Rear
A B C D F
Rear
Q
Front
Inserting a node F in this linked Q

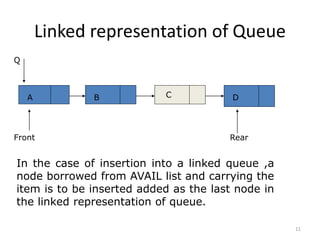
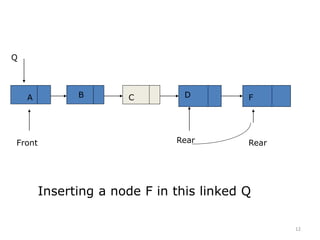
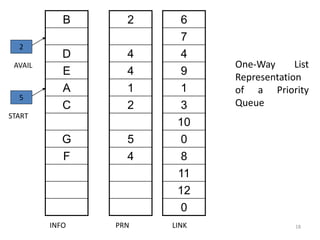
13. 13
Insertion in Linked Representation of Queue
LINKQ_INSERT (INFO,LINK,FRONT,REAR,AVAIL,ITEM)
1. If AVAIL == NULL then write OVERFLOW and Exit
2. Set NEW = AVAIL and AVAIL = LINK[AVAIL]
3. Set INFO[NEW] = ITEM and LINK[NEW] = NULL
4. If (FRONT==NULL) then FRONT = REAR= NEW
Else Set LINK[REAR] = NEW and REAR = NEW
5. Exit

14. 14
A B C D F
Rear
Front
Deleting a node A from this linked Q
Front
Q

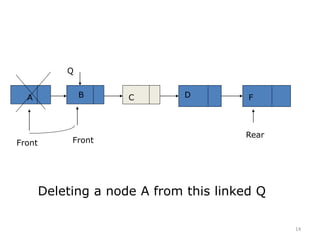
15. 15
Deletion in Linked Representation of Queue
LINKQ_DELETE
(INFO,LINK,FRONT,REAR,AVAIL,ITEM)
1. If FRONT == NULL then Write UNDERFLOW
and Exit
2. Set TEMP = FRONT
3. ITEM = INFO[TEMP]
4. FRONT = LINK[TEMP]
5. LINK[TEMP] = AVAIL and AVAIL = TEMP
6. Exit

16. 16
Priority queues
• It is a collection of elements such that each
element has been assigned a priority such
that
-an element of higher priority
processed before any element of lower
priority
-two elements of equal priority are
processed according to the order in which
they were added to the queue.

17. 17
Priority Queue
• FIFO rules of a queue are relaxed
• Customers or jobs with higher priority are
pushed to front (not rear) of queue
• To implement:
– use an ordinary linked list, which keeps the
items in order from the highest to lowest
priority
– use a treelike structure (heap)

18. 18
B
D
E
A
C
G
F
2
4
4
1
2
5
4
6
7
4
9
1
3
10
0
8
11
12
0
INFO PRN LINK
2
AVAIL
5
START
One-Way List
Representation
of a Priority
Queue

19. 19
Array Representation of a Priority Queue
2
1
0
5
4
2
3
0
1
4
FRONT REAR
1
2
3
4
5
1
2
3
4
5
B
F
A
C X
G
D E
1 2 3 4 5 6
Here X is added in List as priiority 2. That is why it is inserted after C.

20. 20
Application of priority queue
• Application: Scheduling jobs on a workstation
• Priority Queue holds jobs to be performed
and their priorities
• When a job is finished or interrupted, highest-
priority job is chosen using Extract-Max
• New jobs can be added using Insert