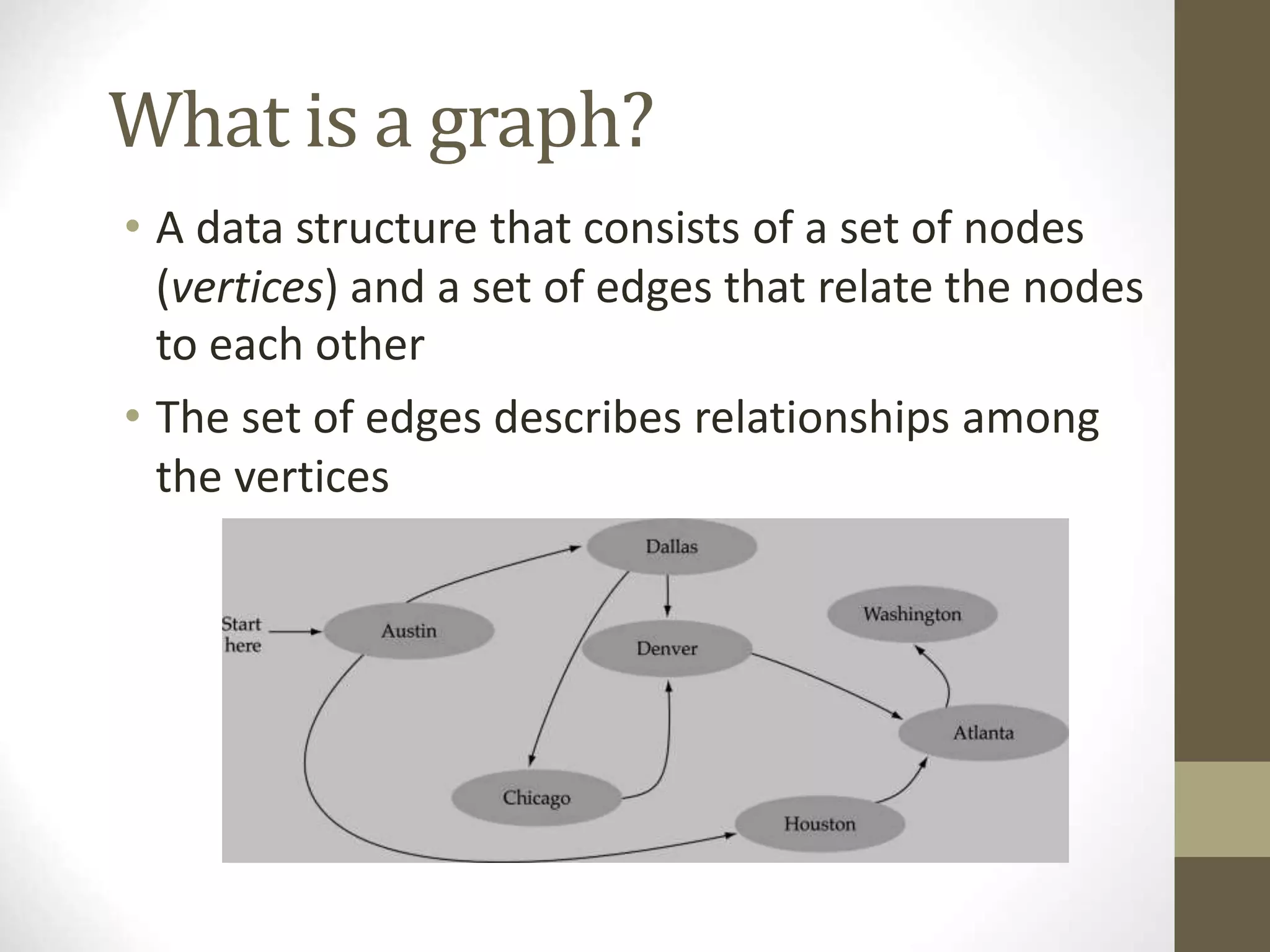
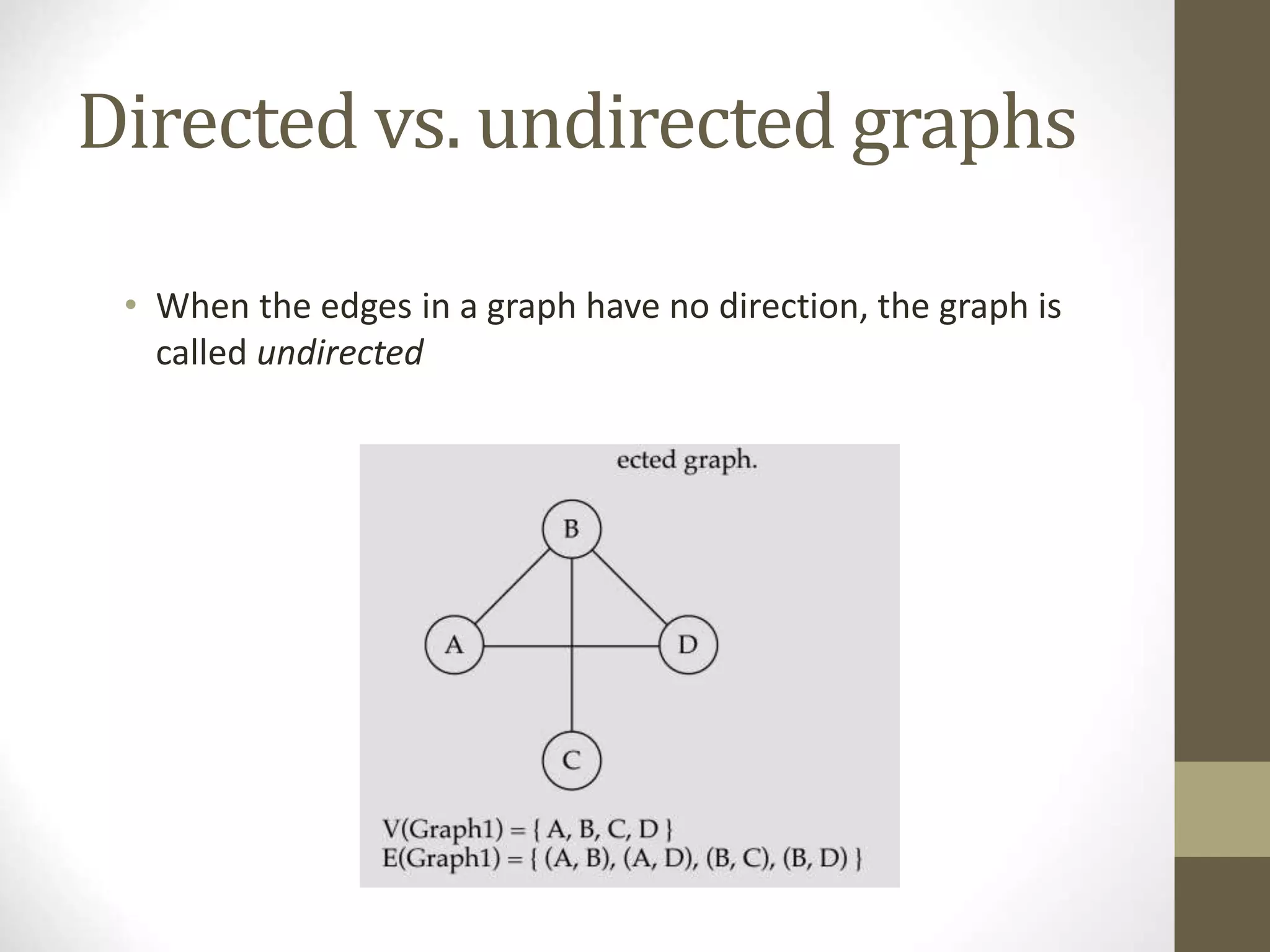
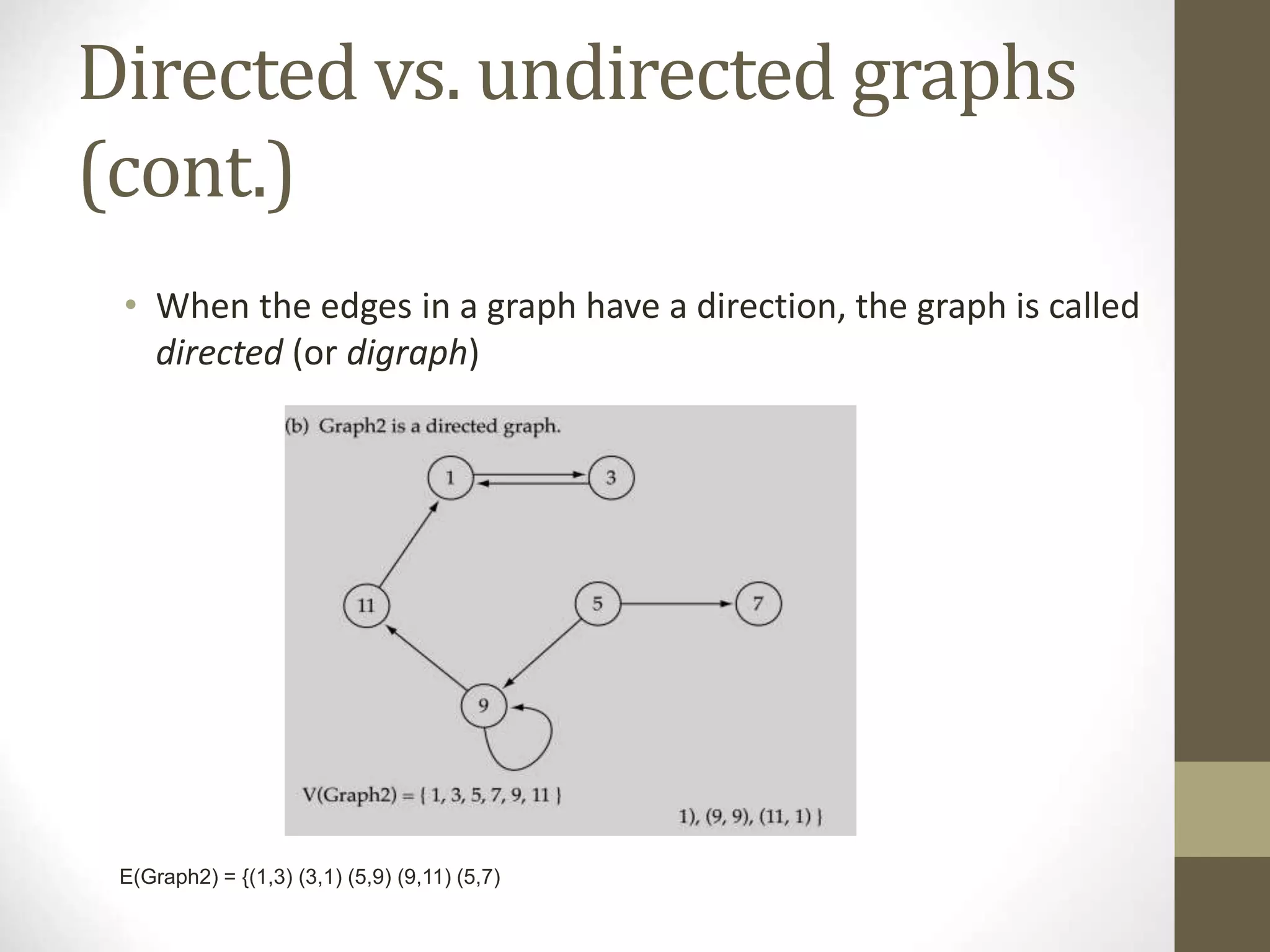
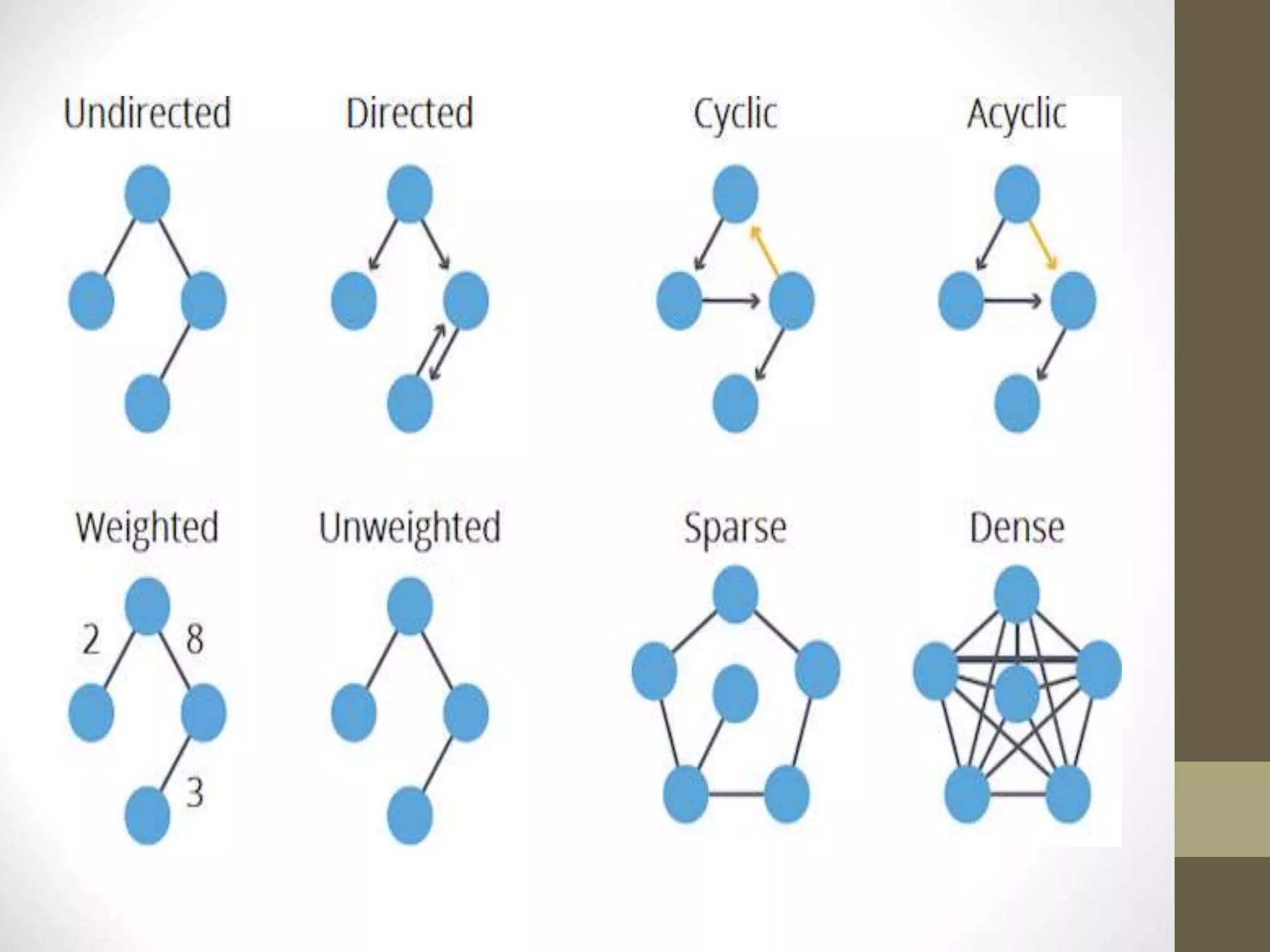
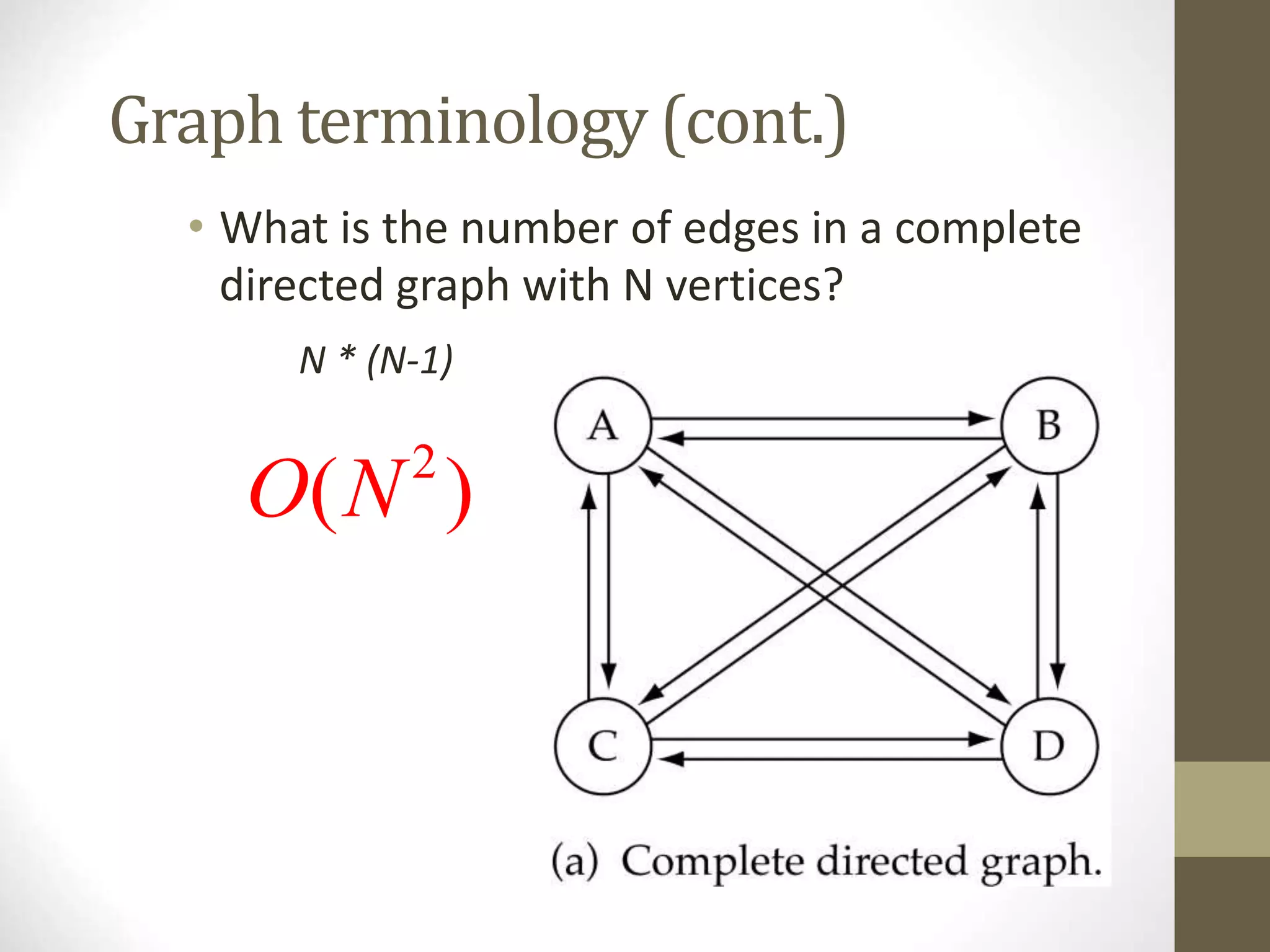
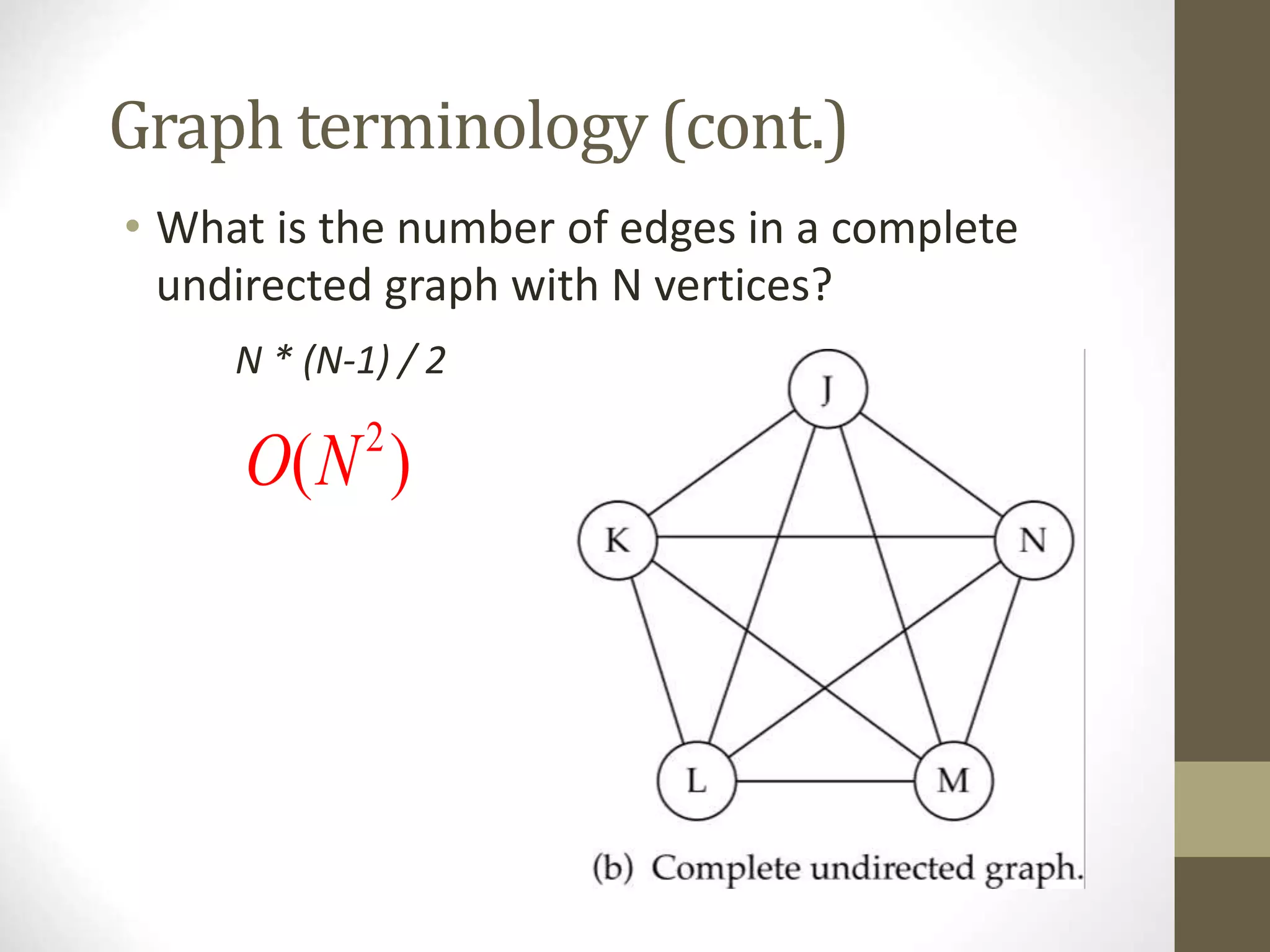
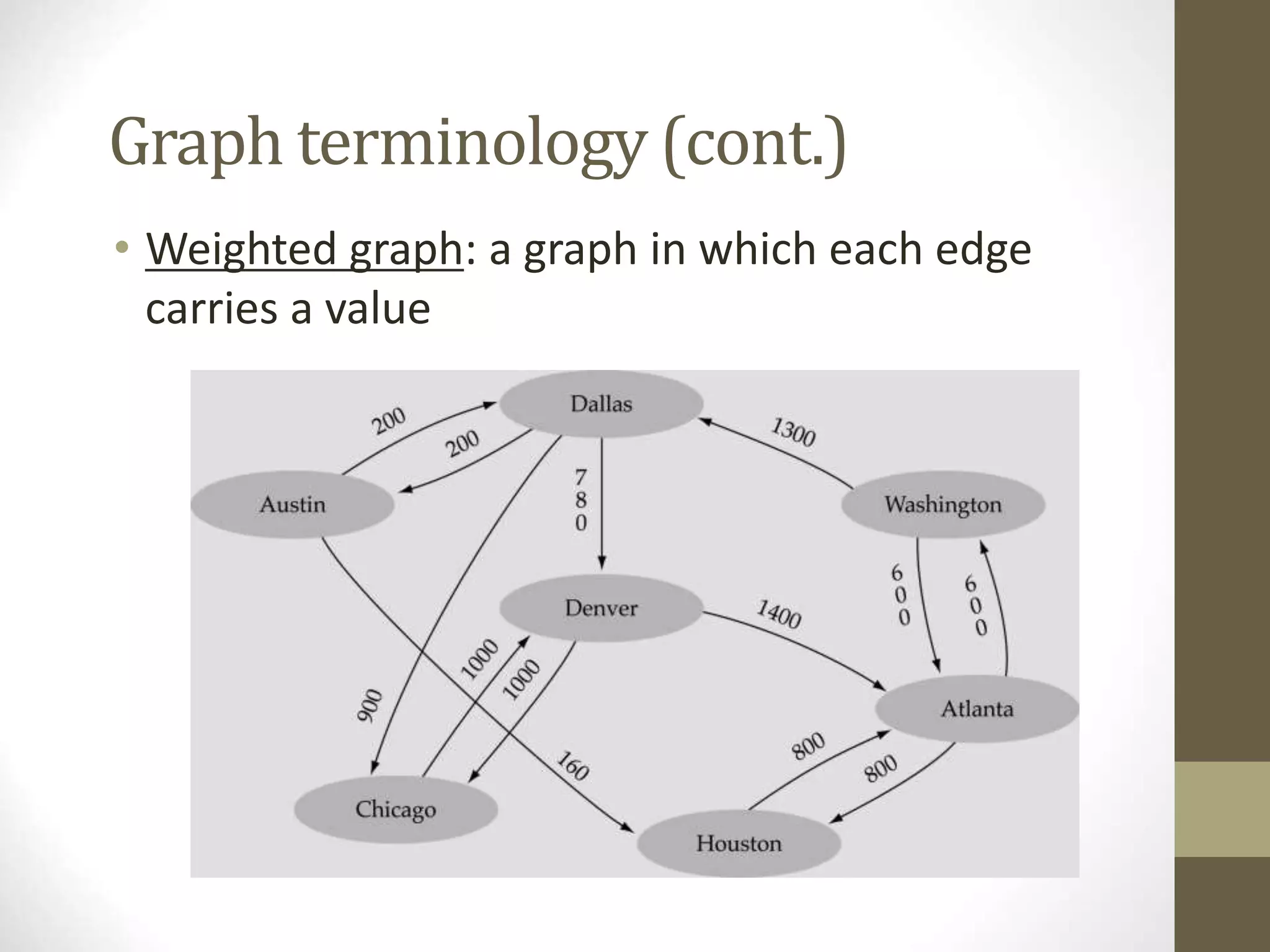
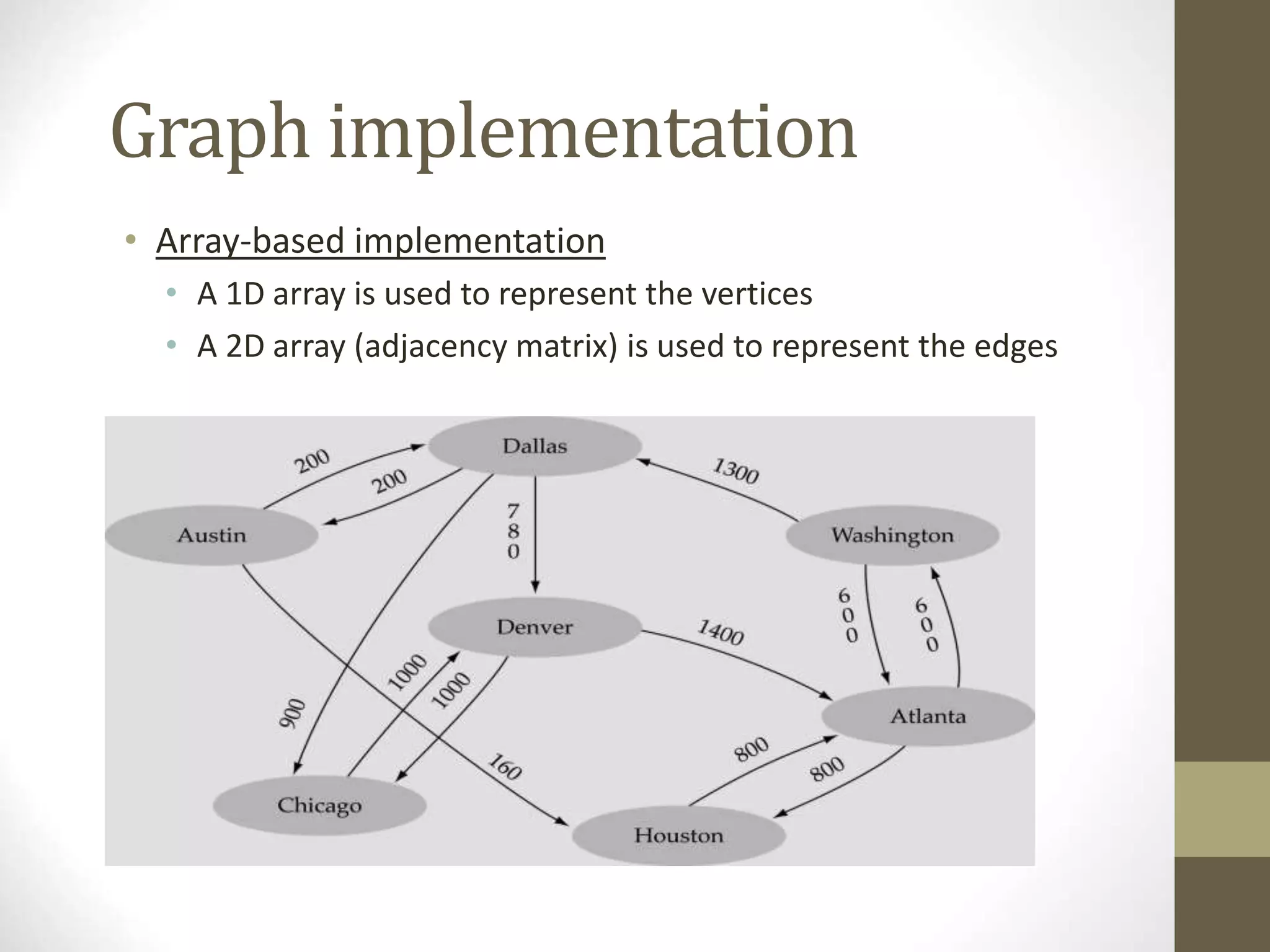
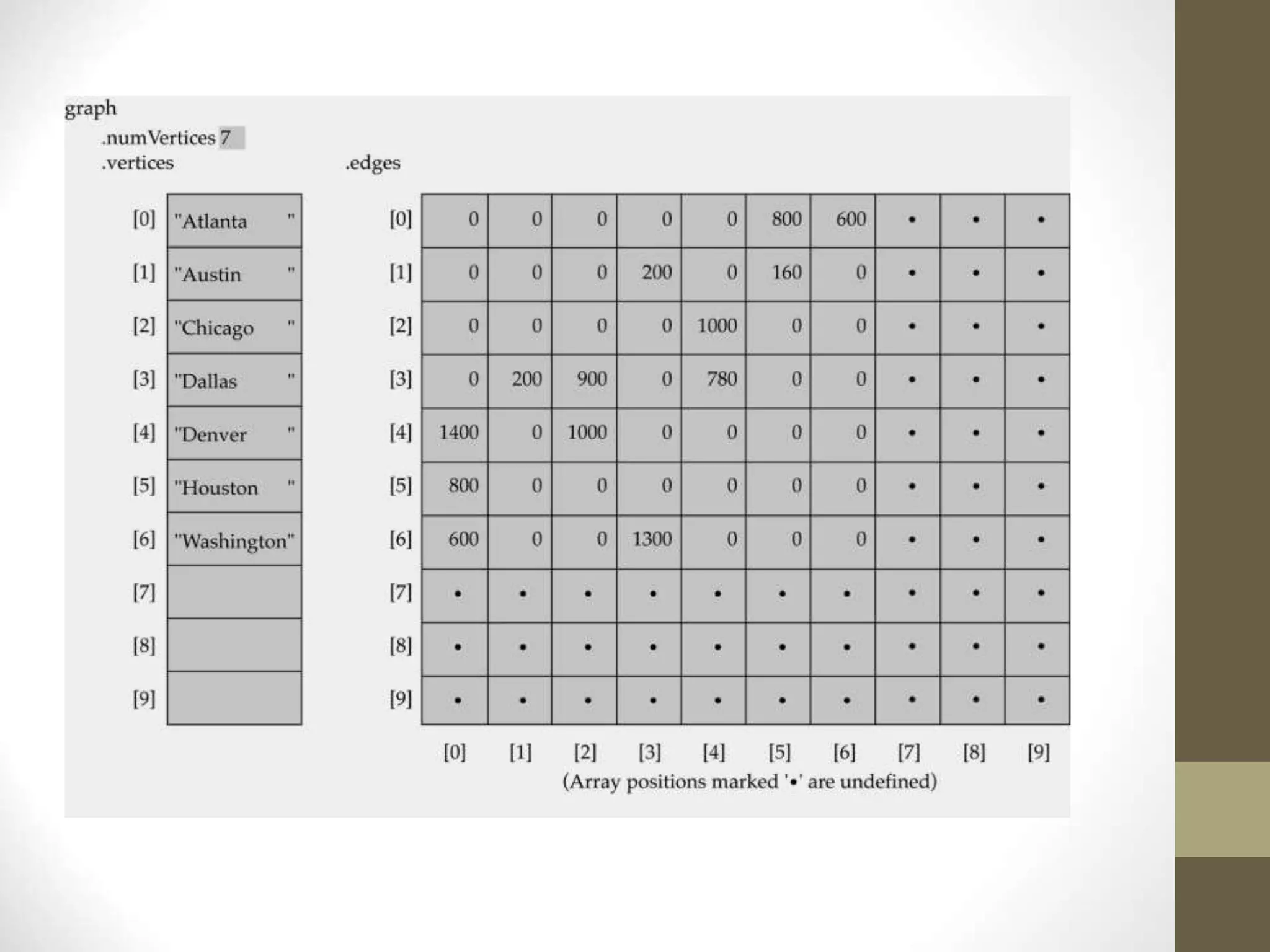
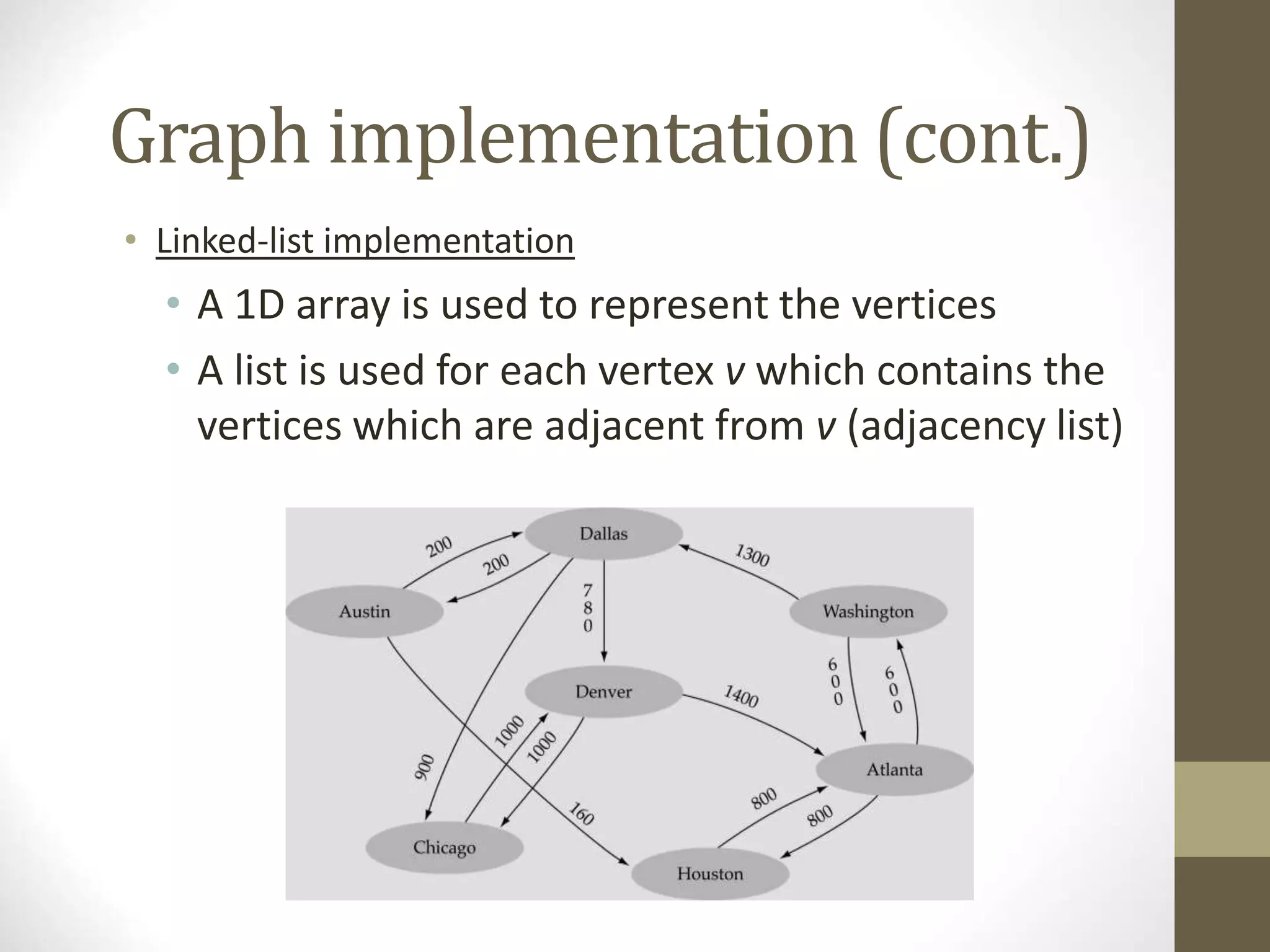
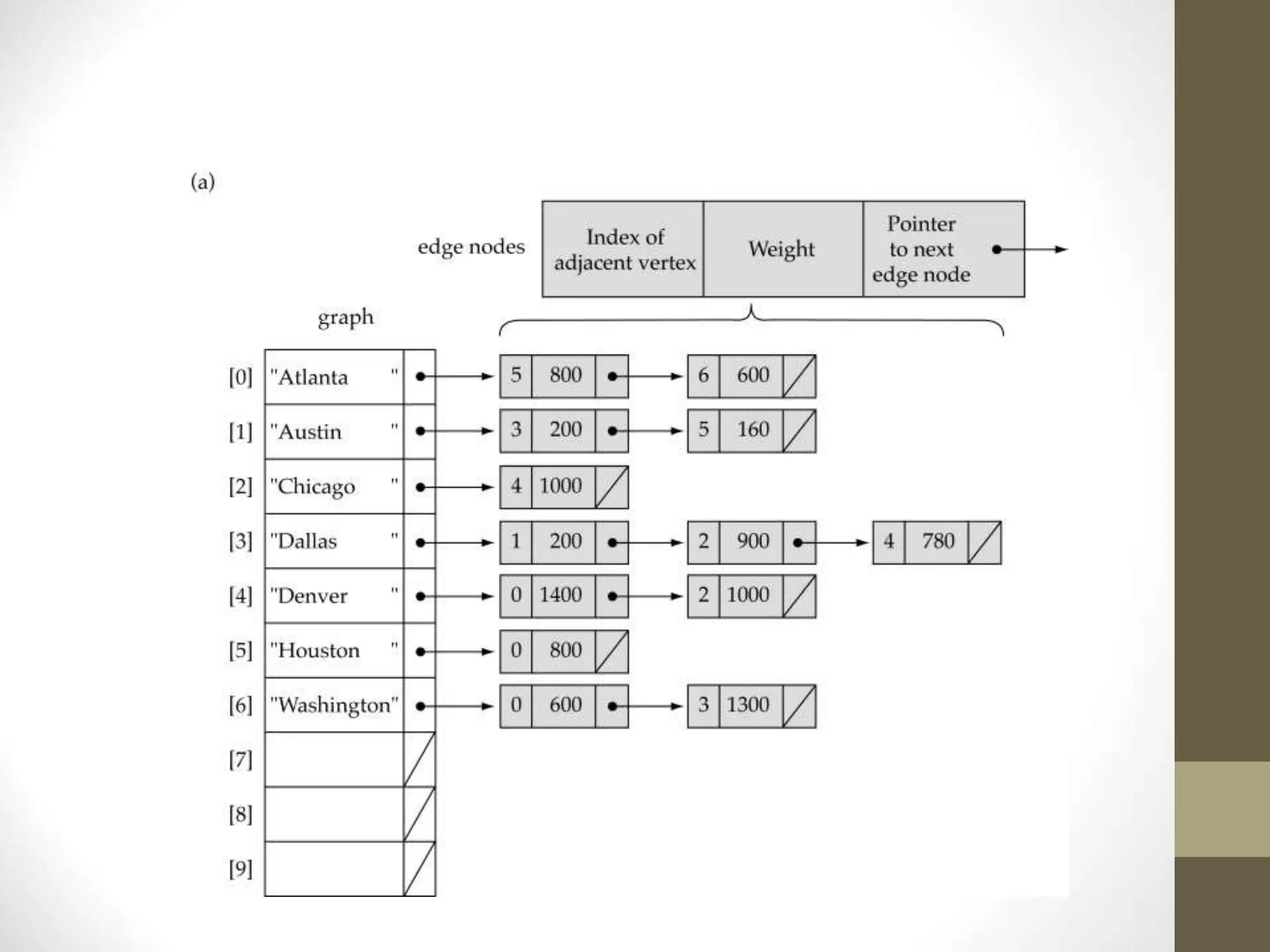
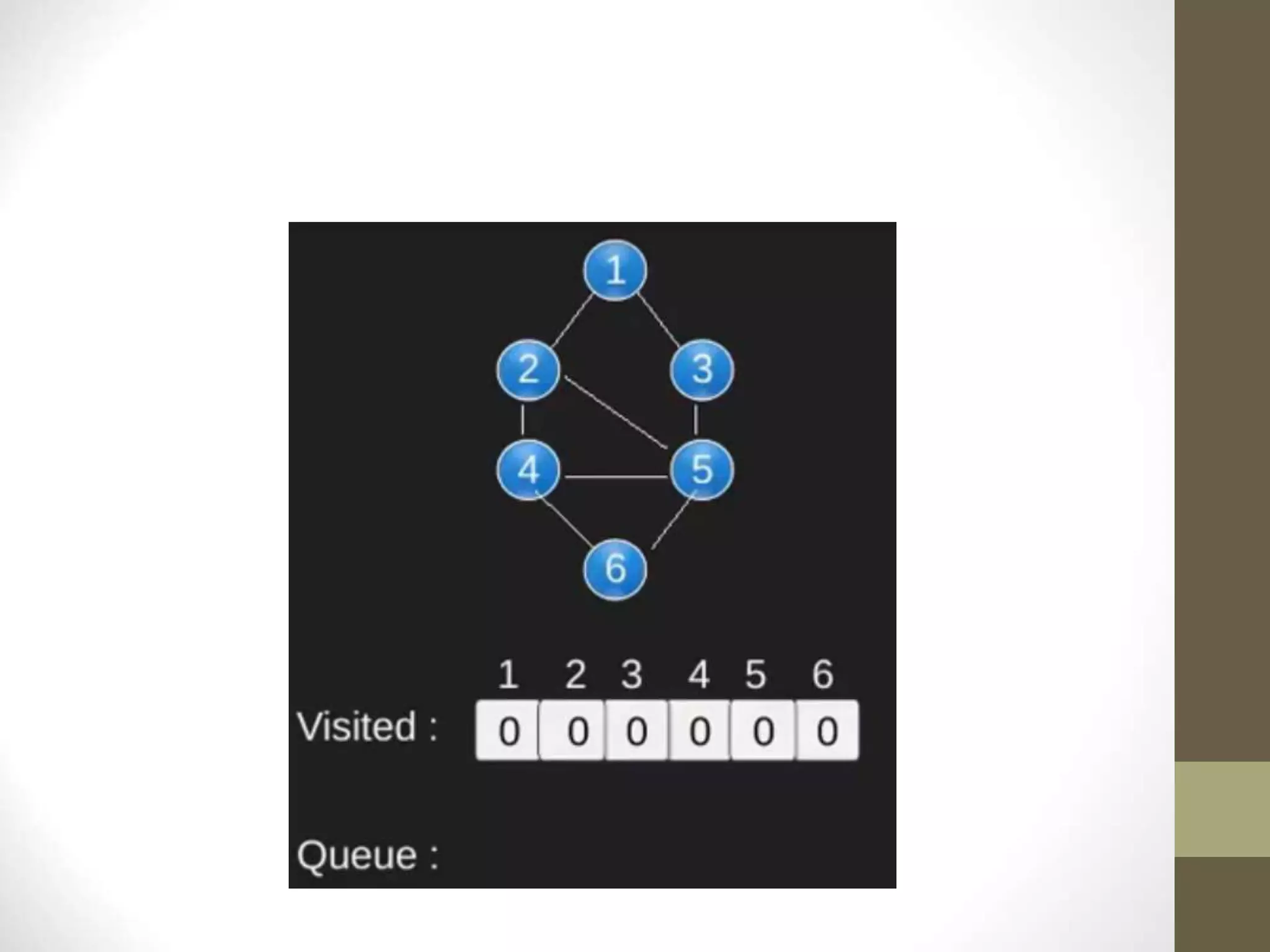
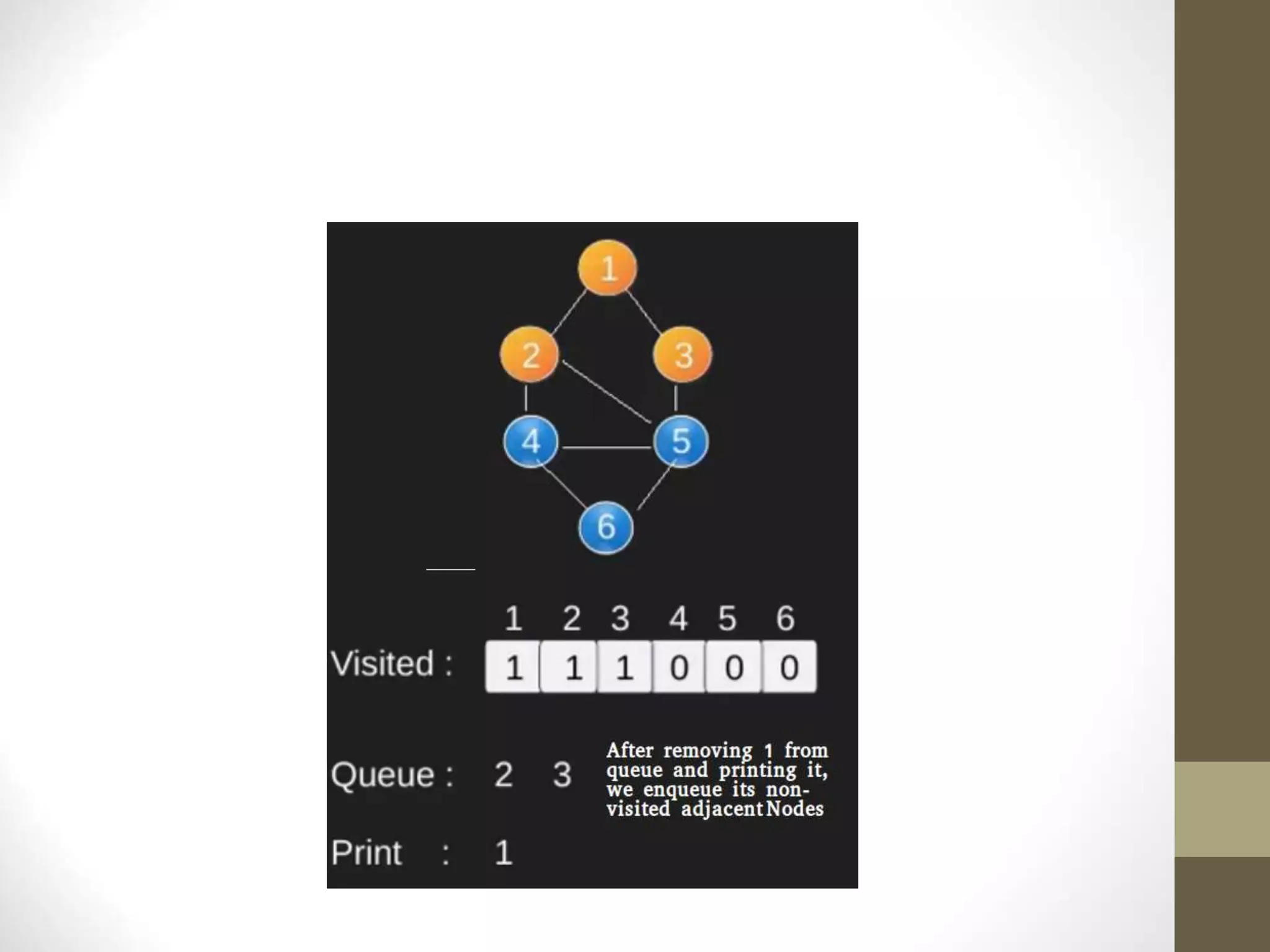
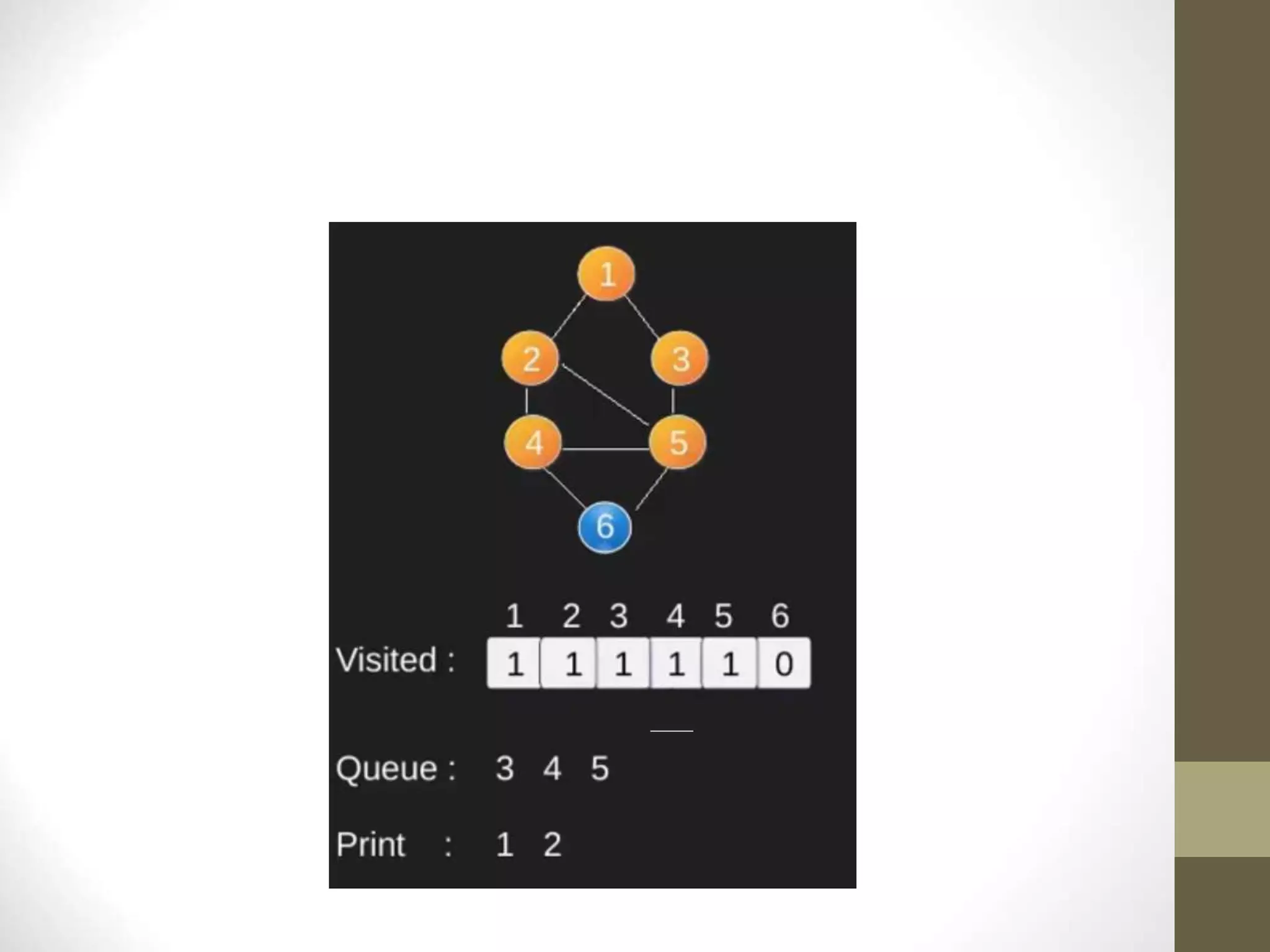
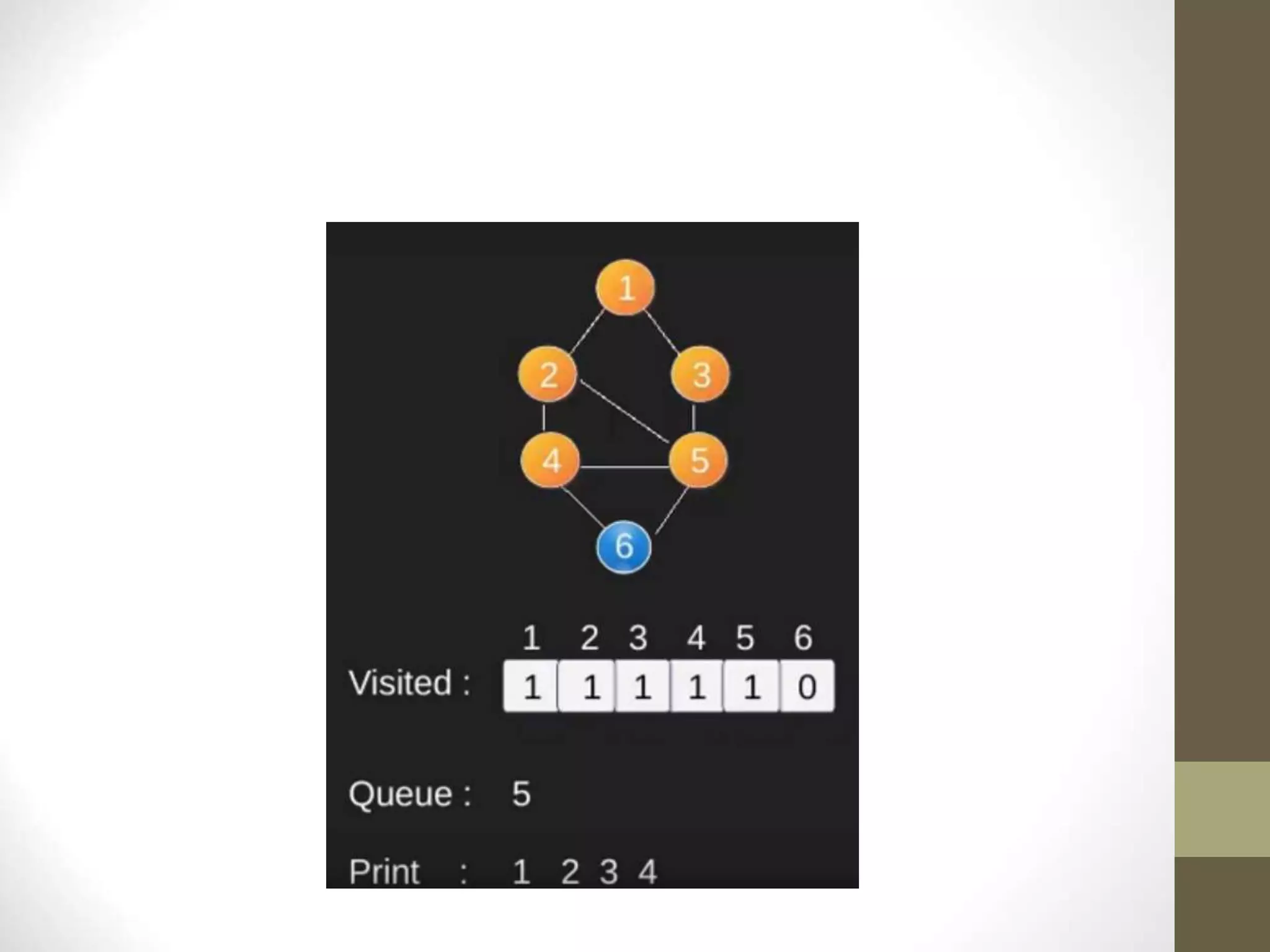
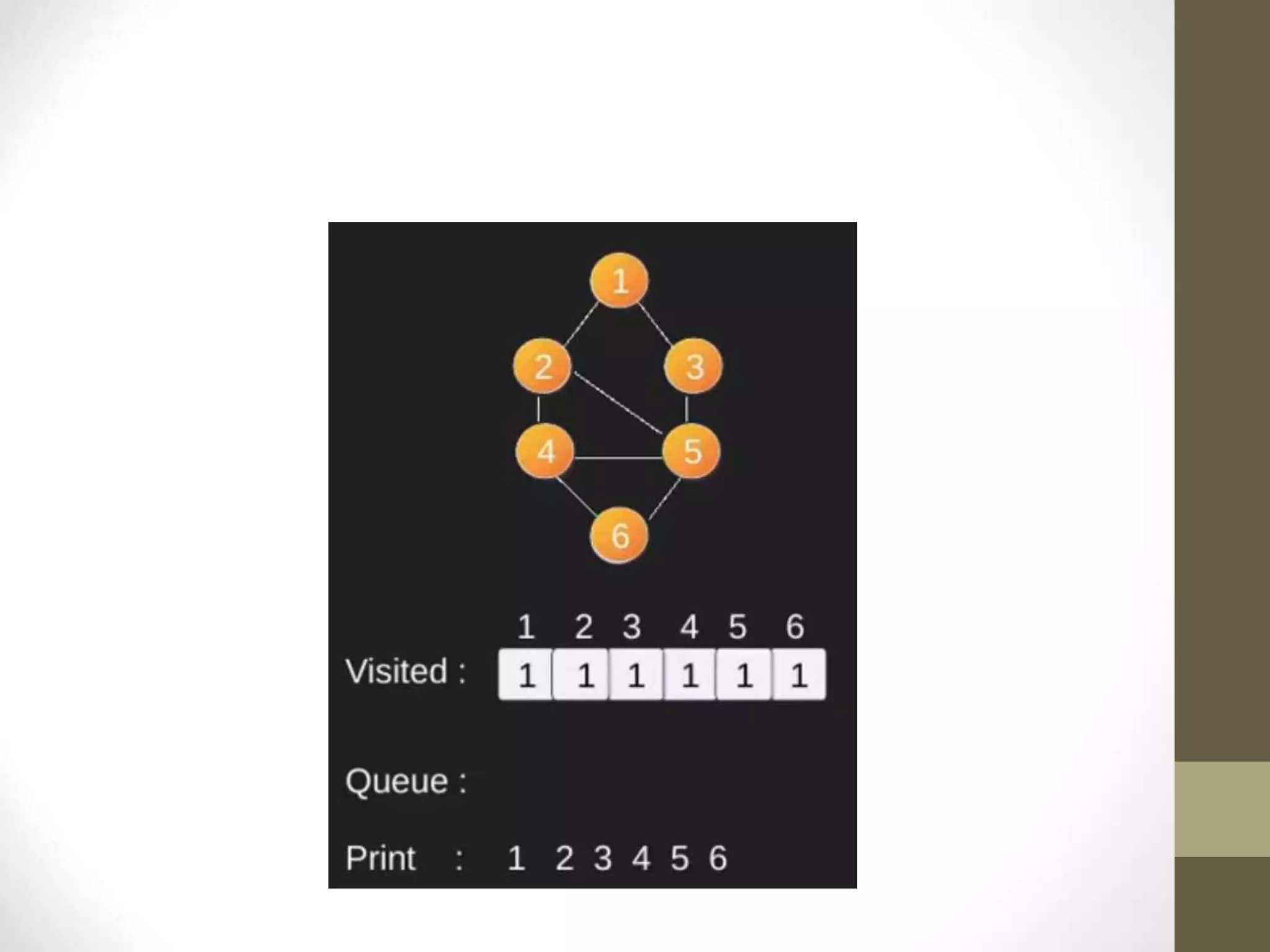
This document defines and explains various graph concepts: - A graph consists of vertices and edges connecting the vertices. Graphs can be directed or undirected. - Common graph terminology includes adjacent vertices, paths, complete graphs, weighted graphs, and representations using adjacency matrices and lists. - Graph searching algorithms like depth-first search (DFS) and breadth-first search (BFS) are used to find paths between vertices. 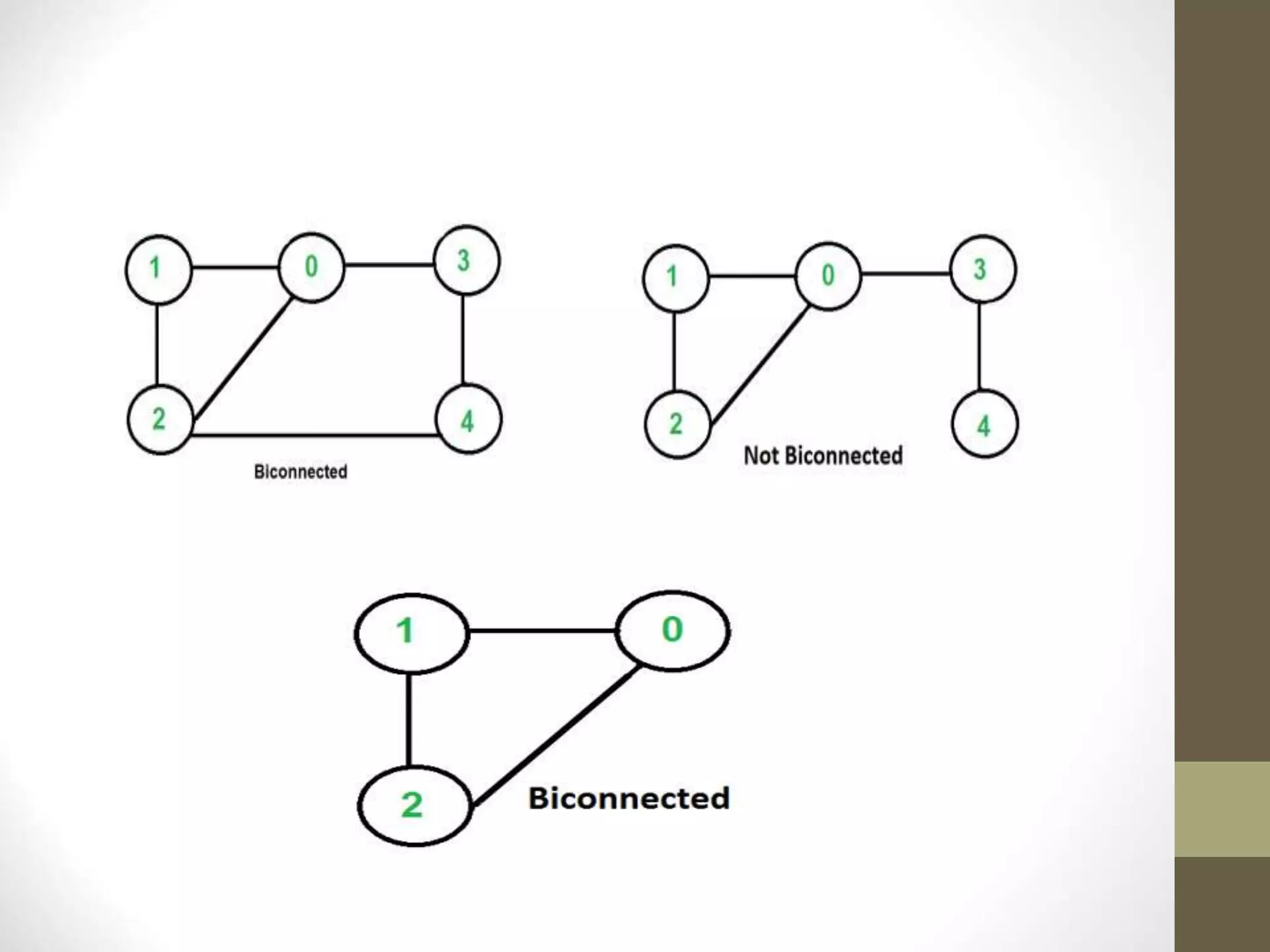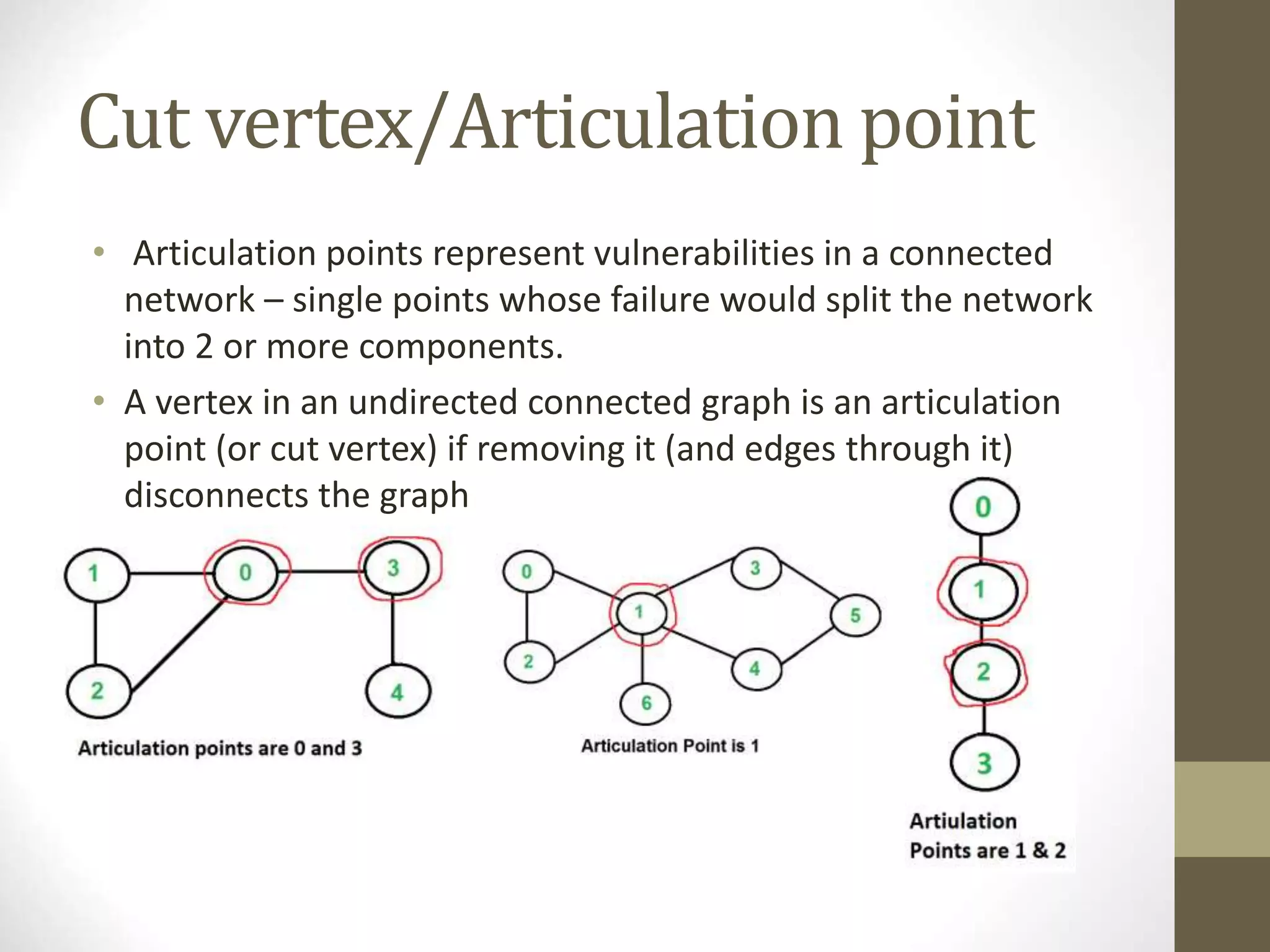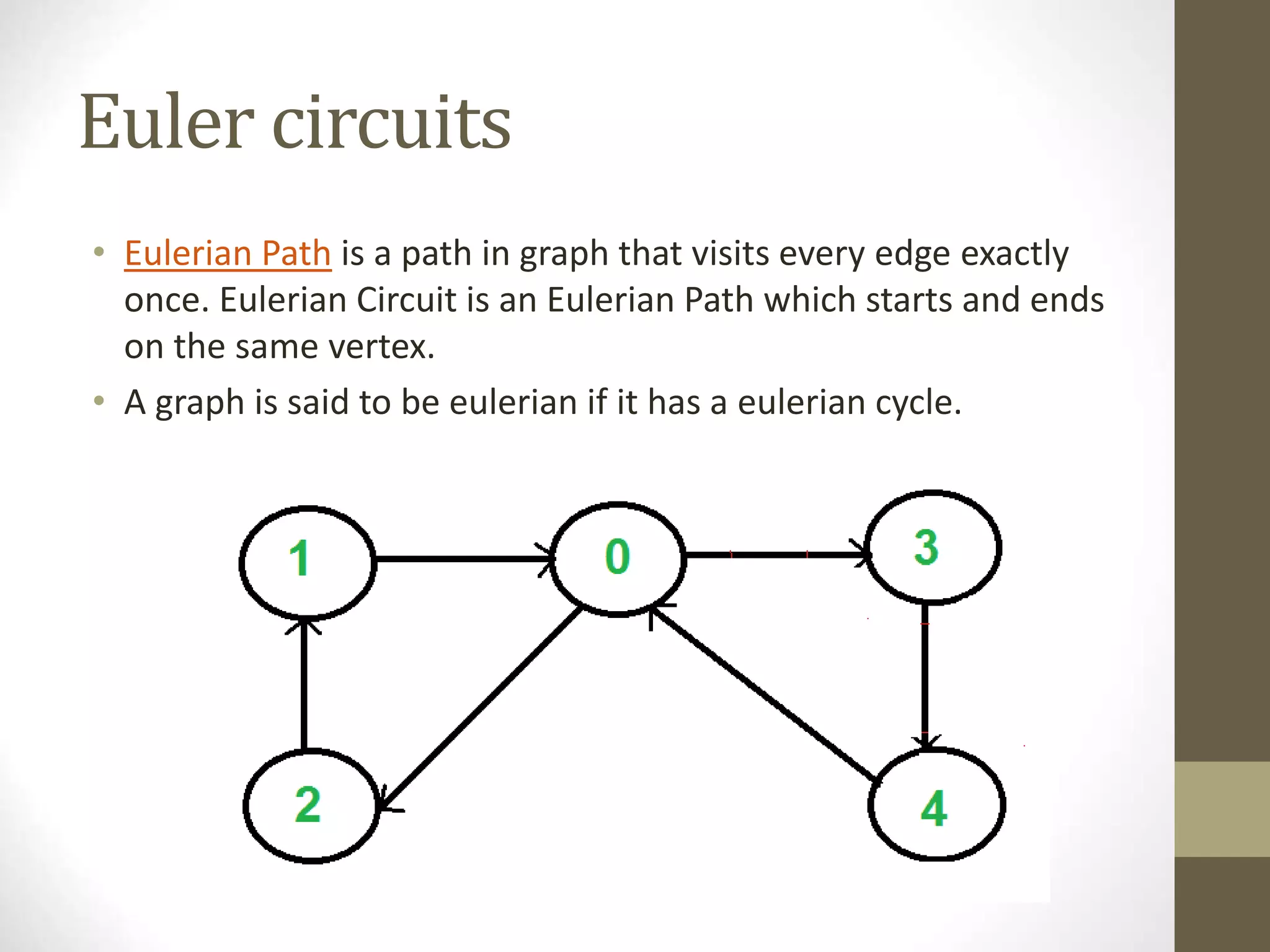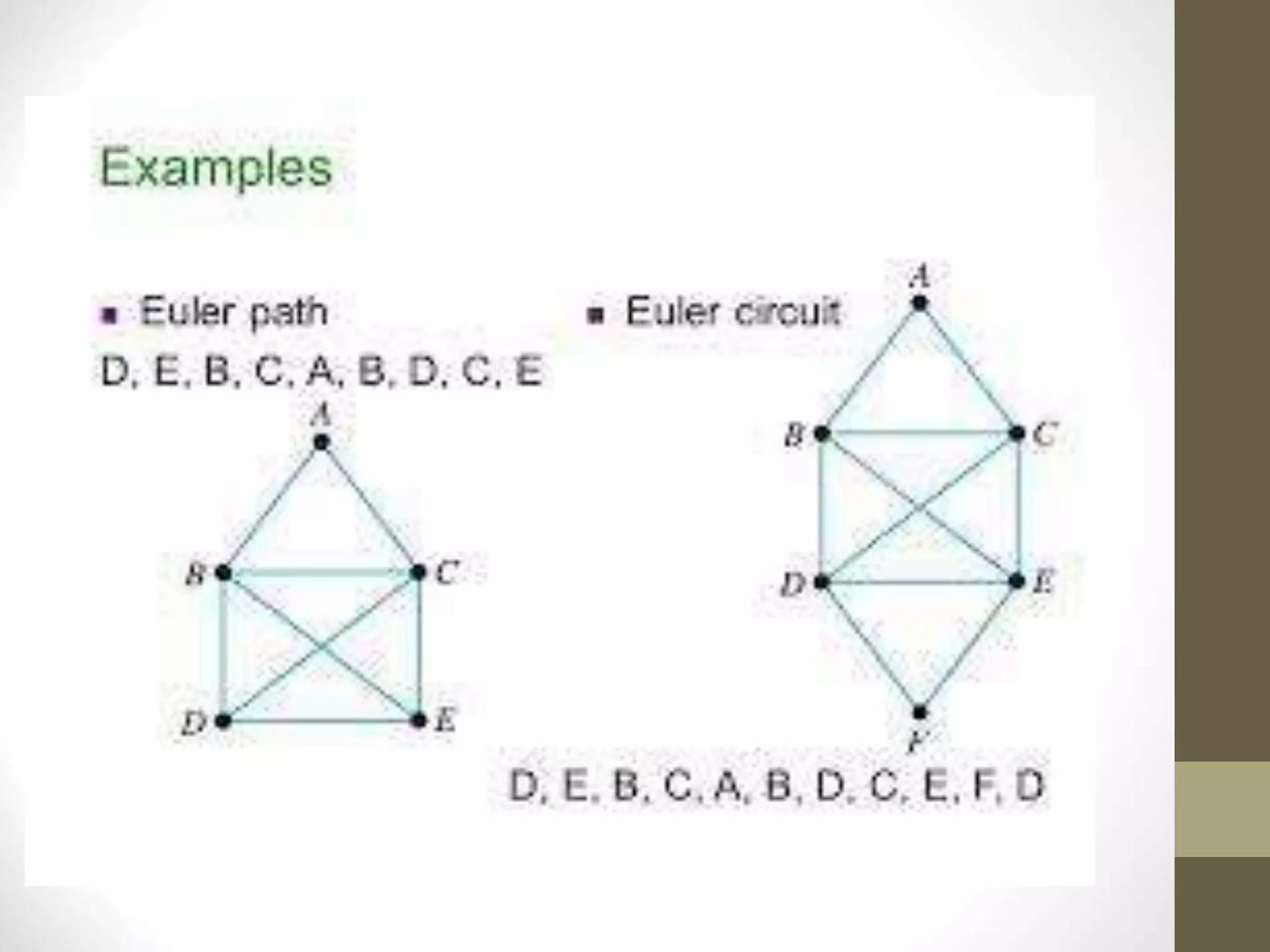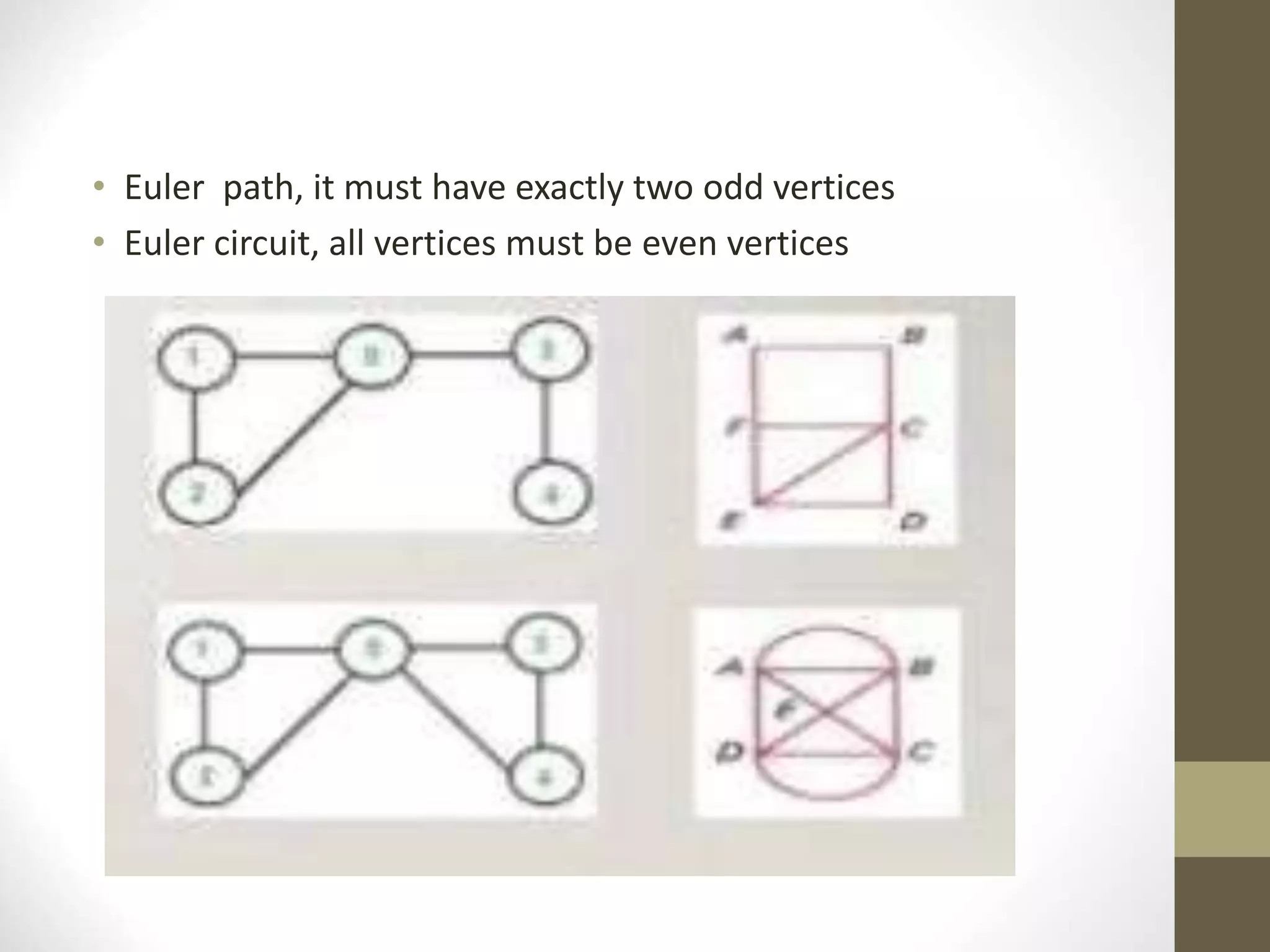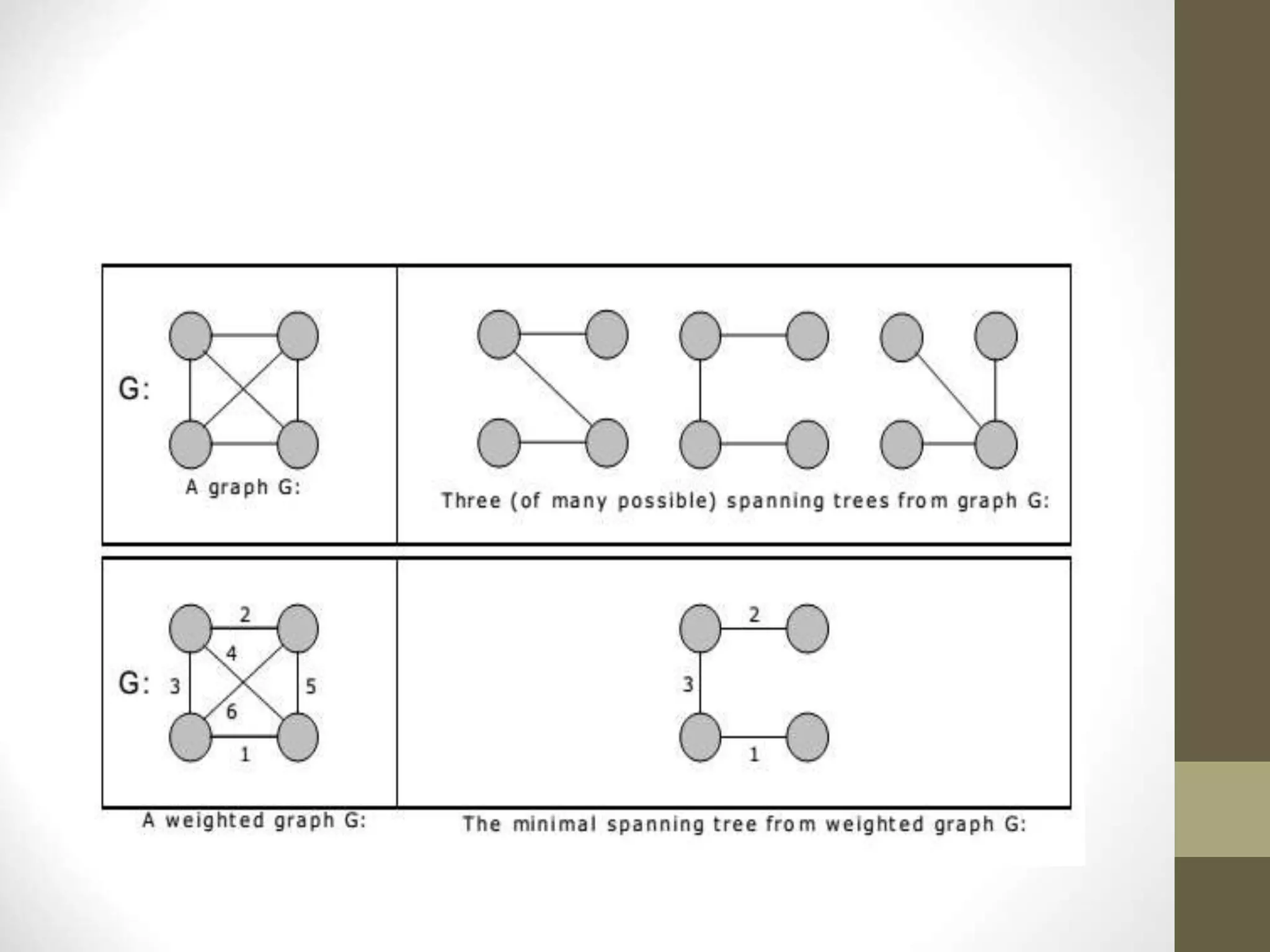- Graphs have applications in areas like maps, networks, and computational systems. Other graph topics covered include topological sorting, biconnectivity, cut vertices, Euler circuits, and minimum spanning trees.

1. Unit 4 - Graphs

2. What is a graph?
• A data structure that consists of a set of nodes
(vertices) and a set of edges that relate the nodes
to each other
• The set of edges describes relationships among
the vertices

3. Definition of graphs
• A graph G is defined as follows:
G=(V,E)
V(G): a finite, nonempty set of vertices
E(G): a set of edges (pairs of vertices)

4. Directed vs. undirected graphs
• When the edges in a graph have no direction, the graph is
called undirected

5. Directed vs. undirected graphs
(cont.)
• When the edges in a graph have a direction, the graph is called
directed (or digraph)
E(Graph2) = {(1,3) (3,1) (5,9) (9,11) (5,7)

6. Trees vs graphs
• Trees are special cases of graphs!!

7. Graph terminology
• Adjacent nodes: two nodes are adjacent if they are connected
by an edge
• Path: a sequence of vertices that connect two nodes in a graph
• Complete graph: a graph in which every vertex is directly
connected to every other vertex
5

9. Graph terminology (cont.)
• What is the number of edges in a complete
directed graph with N vertices?
N * (N-1)
2
( )
O N

10. Graph terminology (cont.)
• What is the number of edges in a complete
undirected graph with N vertices?
N * (N-1) / 2
2
( )
O N

11. Graph terminology (cont.)
• Weighted graph: a graph in which each edge
carries a value

12. Graph implementation
• Array-based implementation
• A 1D array is used to represent the vertices
• A 2D array (adjacency matrix) is used to represent the edges

13. Array-based implementation

14. Graph implementation (cont.)
• Linked-list implementation
• A 1D array is used to represent the vertices
• A list is used for each vertex v which contains the
vertices which are adjacent from v (adjacency list)

15. Linked-list implementation

16. Adjacency matrix vs. adjacency list
representation
• Adjacency matrix
• Good for dense graphs(maximal no of edges) --|E|~O(|V|2)
• Memory requirements: O(|V| + |E|) = O(|V|2 )
• Connectivity between two vertices can be tested quickly
• Adjacency list
• Good for sparse graphs(minimal no of edges) -- |E|~O(|V|)
• Memory requirements: O(|V| + |E|)=O(|V|)
• Vertices adjacent to another vertex can be found quickly

17. Graph searching
• Problem: find a path between two nodes of the graph (e.g.,
Austin and Washington)
• Methods: Depth-First-Search (DFS) or Breadth-First-Search (BFS)

18. Depth-First-Search (DFS)
• What is the idea behind DFS?
• Travel as far as you can down a path
• Back up as little as possible when you reach a "dead end" (i.e.,
next vertex has been "marked" or there is no next vertex)
• DFS can be implemented efficiently using a stack

19. Rules to be followed for DFS
• Rule 1 − Visit the adjacent unvisited vertex. Mark it as visited.
Display it. Push it in a stack.
• Rule 2 − If no adjacent vertex is found, pop up a vertex from
the stack. (It will pop up all the vertices from the stack, which
do not have adjacent vertices.)
• Rule 3 − Repeat Rule 1 and Rule 2 until the stack is empty

20. • https://www.programiz.com/dsa/graph-dfs

21. Breadth-First-Searching (BFS)
• What is the idea behind BFS?
• Look at all possible paths at the same depth before you go at a
deeper level
• Back up as far as possible when you reach a "dead end" (i.e., next
vertex has been "marked" or there is no next vertex)

22. Breadth-First-Searching (BFS) (cont.)
• BFS can be implemented efficiently using a queue
Set found to false
queue.Enqueue(startVertex)
DO
queue.Dequeue(vertex)
IF vertex == endVertex
Set found to true
ELSE
Enqueue all adjacent vertices onto queue
WHILE !queue.IsEmpty() AND !found
• Should we mark a vertex when it is enqueued or
when it is dequeued ?
IF(!found)
Write "Path does not exist"

28. Applications of Graph
• Google maps uses graphs for building transportation
systems
• graph is used to represent networks of communication, data
organization, computational devices etc.
• graphs are used to represent the flow of computation

29. Topological sort
• The topological sort algorithm takes a directed graph and
returns an array of the nodes where each node appears
before all the nodes it points to.
• The ordering of the nodes in the array is called a topological
ordering.
• Topological sorting for Directed Acyclic Graph (DAG) is a linear
ordering of vertices such that for every directed edge u v,
vertex u comes before v in the ordering.
• Topological Sorting for a graph is not possible if the graph is
not a DAG.
• https://www.gatevidyalay.com/topological-sort-topological-
sorting/

30. Bi-connectivity
• An undirected graph is called Biconnected if there are two
vertex-disjoint paths between any two vertices. In a
Biconnected Graph, there is a simple cycle through any two
vertices.
• A graph is said to be Biconnected if:
1) It is connected, i.e. it is possible to reach every vertex from
every other vertex, by a simple path.
2) Even after removing any vertex the graph remains
connected.

32. Cut vertex/Articulation point
• Articulation points represent vulnerabilities in a connected
network – single points whose failure would split the network
into 2 or more components.
• A vertex in an undirected connected graph is an articulation
point (or cut vertex) if removing it (and edges through it)
disconnects the graph

33. Euler circuits
• Eulerian Path is a path in graph that visits every edge exactly
once. Eulerian Circuit is an Eulerian Path which starts and ends
on the same vertex.
• A graph is said to be eulerian if it has a eulerian cycle.

35. • Euler path, it must have exactly two odd vertices
• Euler circuit, all vertices must be even vertices

36. Minimum spanning tree
• A Minimum Spanning Tree(MST) or minimum weight spanning
tree for a weighted, connected, undirected graph is
a spanning tree having a weight less than or equal to the
weight of every other possible spanning tree.
• The weight of a spanning tree is the sum of weights given to
each edge of the spanning tree.

38. Prim’s Algorithm
• Prim's algorithm to find minimum cost spanning tree (as
Kruskal's algorithm) uses the greedy approach. Prim's
algorithm shares a similarity with the shortest path
first algorithms.
• https://www.tutorialspoint.com/data_structures_algorithms/
prims_spanning_tree_algorithm.htm
• https://www.youtube.com/watch?v=4ZlRH0eK-qQ
• https://www.geeksforgeeks.org/difference-between-prims-
and-kruskals-algorithm-for-mst/

39. Kruskal’s algorithm
• Kruskal's Algorithm is used to find the minimum spanning
tree for a connected weighted graph.
• The main target of the algorithm is to find the subset of edges
by using which, we can traverse every vertex of the graph.
• https://www.geeksforgeeks.org/kruskals-minimum-spanning-
tree-algorithm-greedy-algo-2/