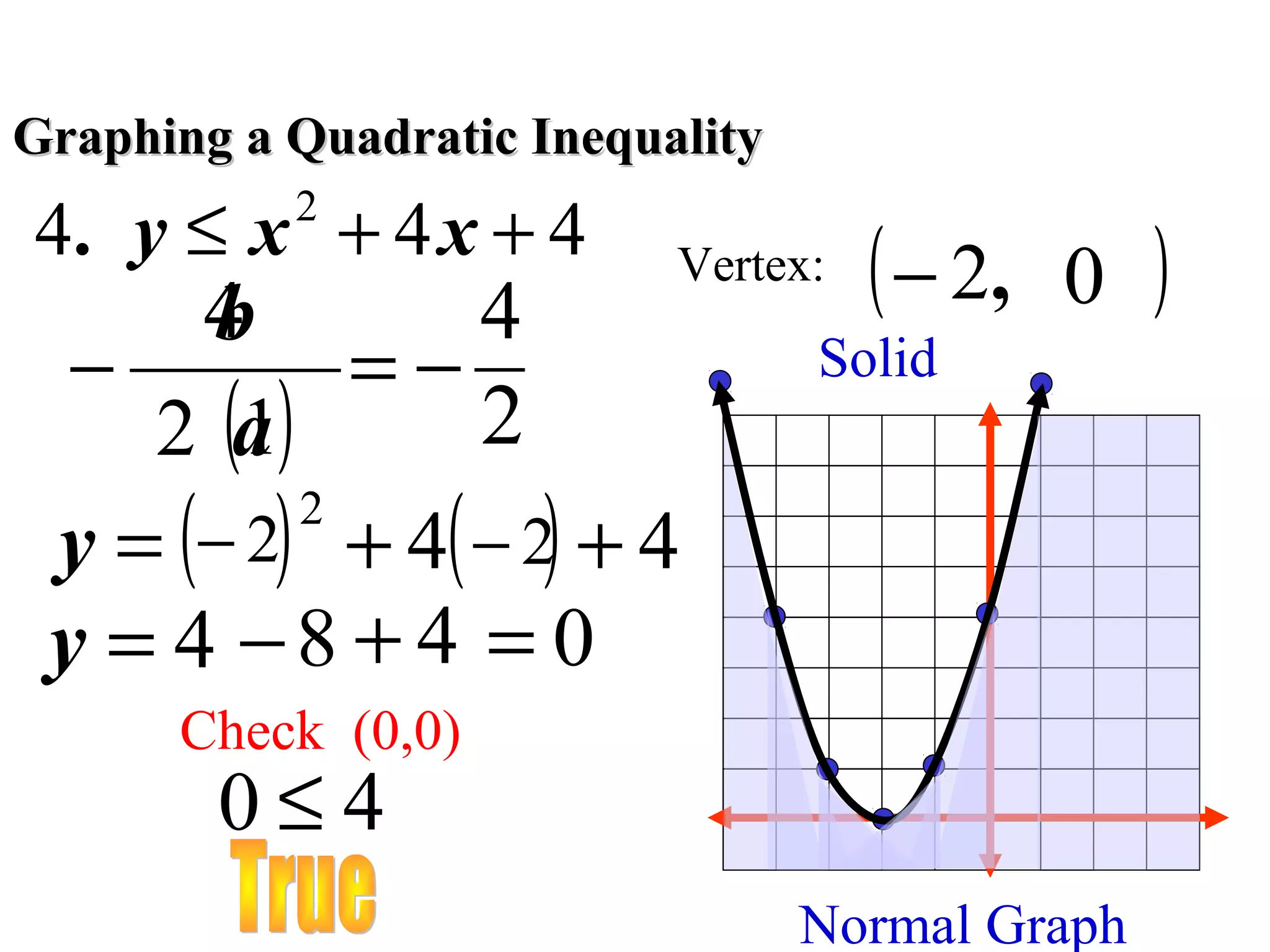
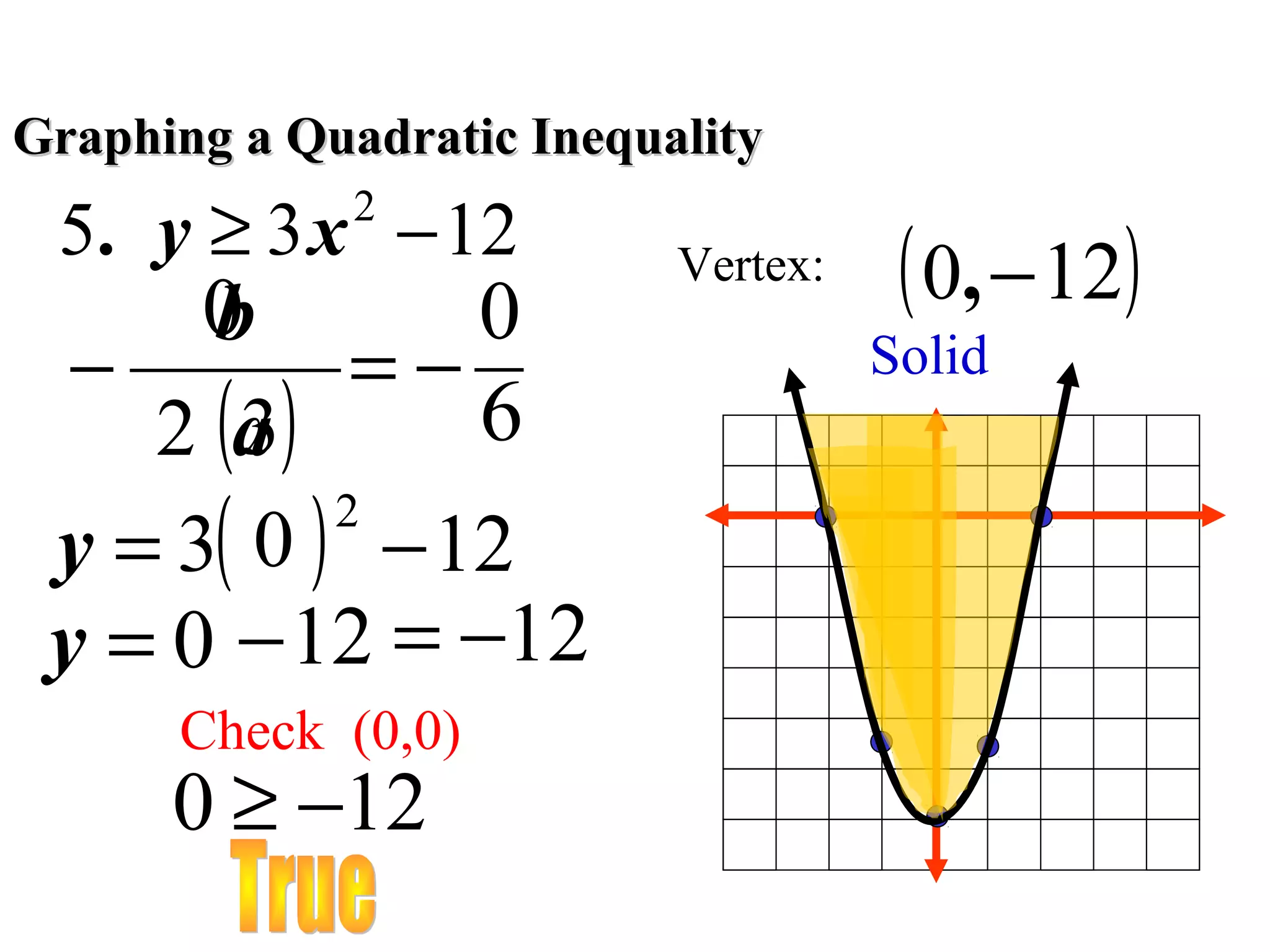
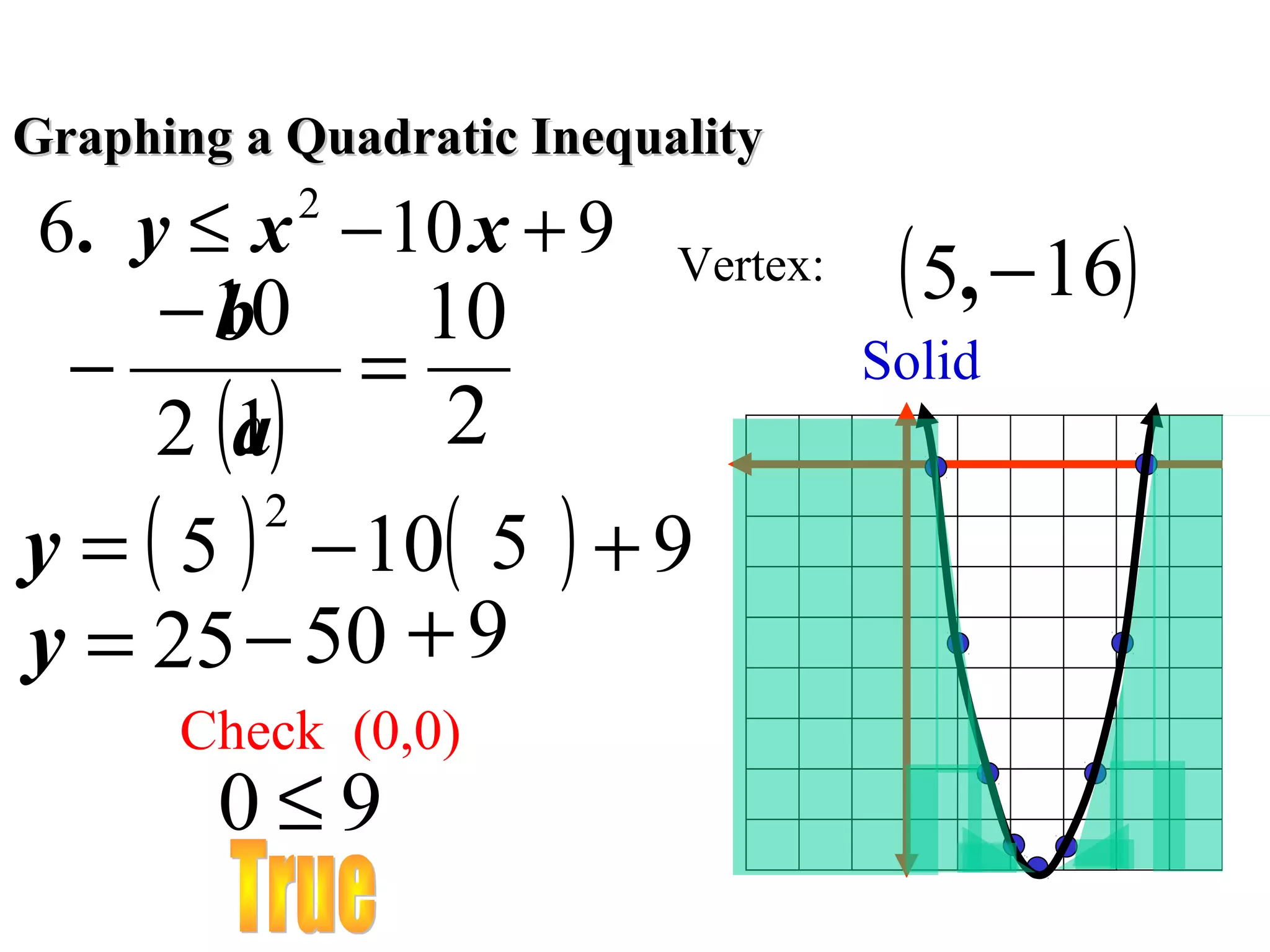
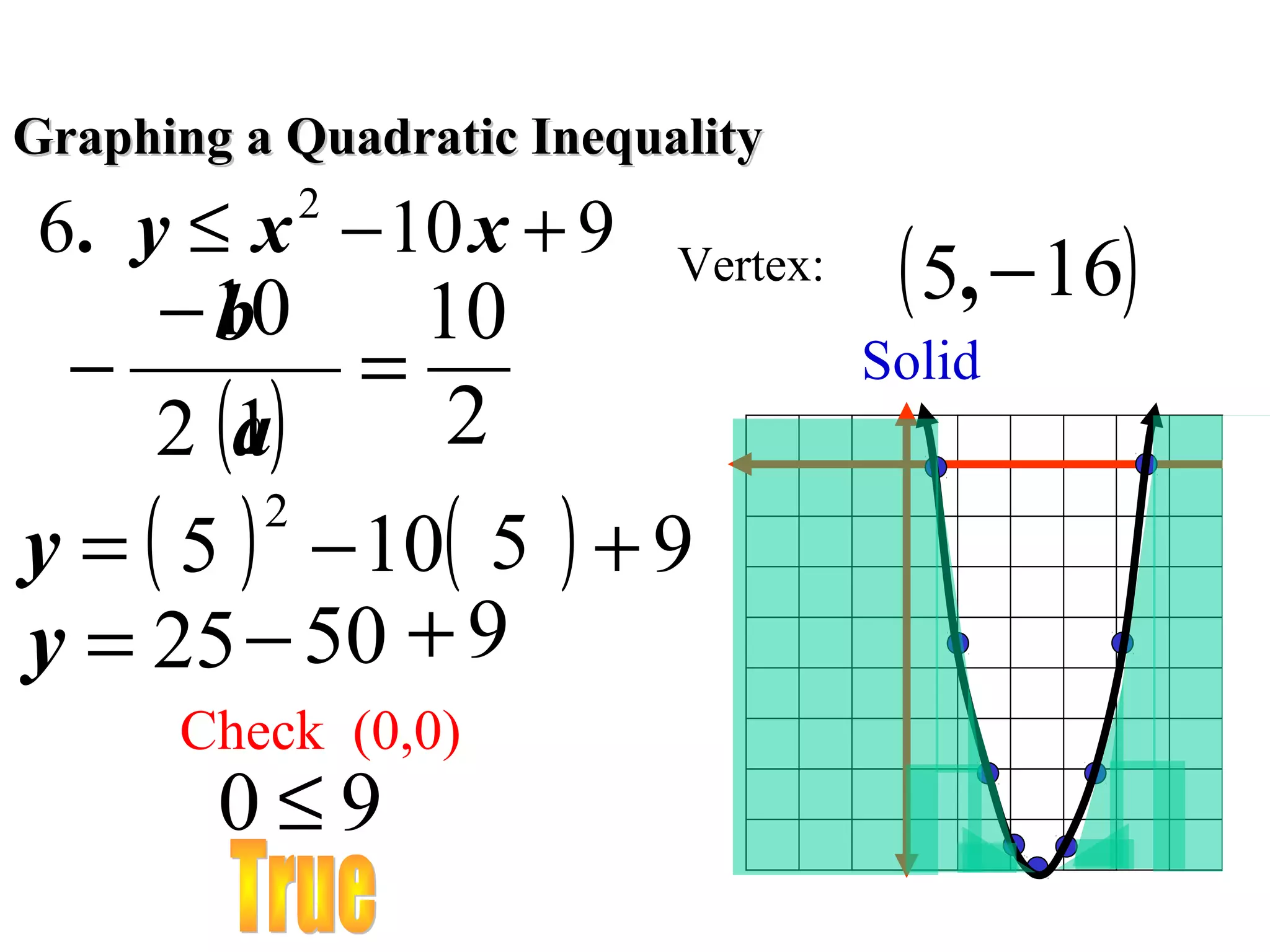
This document discusses checking solutions to quadratic inequalities and graphing quadratic inequalities. It provides examples of checking if an ordered pair is a solution to an inequality and finding the vertex of a quadratic function to graph it as a solid curve below or above the vertex based on whether the inequality is ≤ or ≥.

1. 5.8 Quadratic Inequalities
Checking Solutions
Decide whether the ordered pair is a solution, of the
inequality.
) x
1
2.− y < 2 (1x + 1 ,
2
−1 < 2 + 1
−1 < 3
(1,−1)

2. Checking Solutions
Decide whether the ordered pair is a solution, of the
inequality.
(,
3 x
3.− y > 2 − 3 x2 ) ( 2,−3)
2
−3 > 4 −6
− 3 > −2

3. Graphing a Quadratic Inequality
4. y ≤ x + 4 x + 4
2
Vertex:
4
4
b
=−
−
2
1
2 (a )
2
y = (− 2) + 4( − 2) + 4
y = 4 −8 + 4 = 0
( − 2,
0
Solid
Check (0,0)
0≤4
Normal Graph
)

4. Graphing a Quadratic Inequality
5. y ≥ 3 x − 12
2
0
0
b
=−
−
6
3
2 (a )
2
y = 3( 0 ) − 12
y = 0 − 12 = −12
Check (0,0)
0 ≥ −12
Vertex:
( 0, − 12)
Solid

5. Graphing a Quadratic Inequality
6. y ≤ x − 10 x + 9
2
Vertex:
− 10
10
b
=
−
2
1
2 (a)
2
y = ( 5 ) − 10( 5 ) + 9
y = 25 − 50 + 9
Check (0,0)
0≤9
( 5, − 16)
Solid

6. Graphing a Quadratic Inequality
6. y ≤ x − 10 x + 9
2
Vertex:
− 10
10
b
=
−
2
1
2 (a)
2
y = ( 5 ) − 10( 5 ) + 9
y = 25 − 50 + 9
Check (0,0)
0≤9
( 5, − 16)
Solid