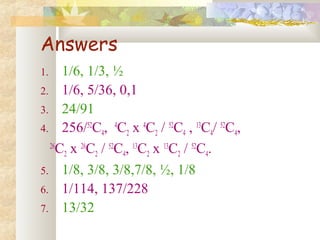
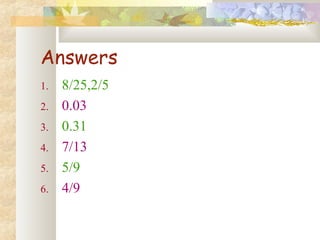
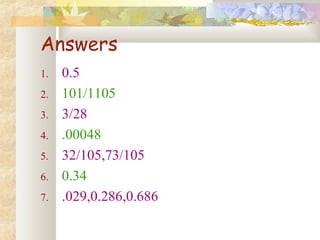
This document discusses probability and provides examples of calculating probabilities of events. Some key points covered include: - Probability allows quantifying the variability in outcomes of experiments with uncertain results. - Key concepts like sample space, events, outcomes, mutually exclusive events, independent events are defined. - Probability is calculated as the number of favorable outcomes divided by the total number of outcomes. - Examples of probability calculations involving dice rolls, card draws, and coin tosses are provided. - Theorems like addition rule, multiplication rule, and conditional probability are discussed.

1. Probability

2. Probability
 It allows us to quantify the
variability in the outcome of an
experiment whose exact result can’t
be predicted with certainty.

3. Definitions
 Random Experiment
A random experiment or trial is one which
when conducted successively under the
identical conditions, the result is not
unique but may be any one of the various
possible outcomes.
Example: Tossing a fair coin in an experiment.

4.  Sample space:
The set of all possible outcomes is a
sample space.
 Event:
Outcome or combination of outcomes
 Outcome:
The result of an event which we finally
achieved is called an outcome or a
sample point.

5. Types of Events
 Mutually exclusive events:
Two events are said to be mutually
exclusive or incompatible, when both
cannot happen simultaneously in a single
trial. AÇB=Æ
Example: Toss of a coin (either head will
occur or tail in a single throw)

6.  Independent and dependent events
Two or more events are independent when
the outcome of one does not affect, and is
not affected by the other.
Example: if a coin is tossed twice, the result
of the second throw would not be
affected by the result of the first throw
P(AÇB)=P(A).P(B)
• Dependent events: occurrence of one
event affects probability of happening of
other.

7.  Equally likely events: events are
called equally likely if they have the
same chance of occurrence.
Example: Throw of unbiased coin (both
head and tail have equal chance of
occurrence.)

8. Probability
Numerical measure (between 0 and 1
inclusively) of the likelihood or chance of
occurrence of an uncertain event
P(E) = (NO. OF FAVOURABLE OUTCOMES)
(NO. OF TOTAL OUTCOMES)
0£ P(E) £ 1

9. Questions for practice
 A uniform die is thrown. Find the probability
that the number on it is
(i) Five (ii) greater than 4 (iii)Even no.
2. In a single throw with two uniform dice, find the
probability of throwing
(i) Both the dice show the same number
(ii)A total of Eight (iii) a total of 13
(iv) Total of the numbers on the dice is any
number from 2 to 12, both inclusive.
3. A bag contains 4 white, 5 red and 6 green
balls.Three balls are drawn at random.What is
the chance that a white, a red and a green ball
is drawn?

10. 4. Four cards are drawn at random
from a pack of 52 cards.Find the
probability that
 They are a king, a queen , a jack or an
ace.
 Two are kings and two are aces.
 All are diamonds.
 Two are red and two are black.
 There are two cards of clubs and two
cards of diamonds.

11. 5. Three unbiased coins are
tossed.What is the probability of
obtaining:
 All heads
 Two heads
 One head
 At least one head
 At least two heads
 All tails

12. 6. Five men in a company of 20 are
graduates.If 3 men are picked out of the
20 are random, what is the probability
that they all are graduates?What is the
probability of at least one graduate?
7. Three groups of workers contain 3 men
and one women, 2 men and 2 women, and 1
man and 3 women respectively.One worker
is selected at random from each
group.What is the probability that the
group selected consists of 1 man and 2
women?

13. Answers
1. 1/6, 1/3, ½
2. 1/6, 5/36, 0,1
3. 24/91
4. 256/52C4, 4C2 x 4C2 / 52C4 , 13C4/ 52C4,
26C2 x 26C2 / 52C4, 13C2 x 13C2 / 52C4.
5. 1/8, 3/8, 3/8,7/8, ½, 1/8
6. 1/114, 137/228
7. 13/32

14. Some Important Results-
• 0 £ P(A) £ 1 for all A
• P(S) = 1
• P(Ac) = 1 – P(A) for all A
• P(A È B) = P(A) + P(B) – P(A Ç B)
for all A, B

15. Theorems Of Probability
Addition theorem:
For two disjoint or mutually exclusive events A&B
(i.e P(A Ç B) =0 Since A Ç B=Æ )
P(A È B) = P(A) + P(B)
OR
P(A OR B)=P(A)+P(B)
OR
P(A+B)=P(A)+P(B)

16. When events are not mutually exclusive i.e
P(A Ç B)≠0
P(A È B) = P(A) + P(B) – P(A Ç B)
OR
P(A OR B) = P(A) + P(B) – P(A AND B)
OR
P(A + B) = P(A) + P(B) – P(A.B)
For three events A,B & C,
P(A È B È C) = P(A)+P(B)+P( C )-P(A ÇB)-P(B ÇC)-P(A ÇC)
+P(A ÇB ÇC)

17. Questions for practice
1. From 25 tickets marked with first 25 numerals,
one is drawn at random.Find the chance that
(i) Multiple of 5 or 7.
(ii) Multiple of 3 or 7.
2. Of 1000 assembled components,10 has a working
defect and 20 have a structural defect.There is a
good reason to assume that no components has
both defects.What is the probability that
randomly chosen component will have either type
of defect?

18. 3. The probability that a contractor will get a
plumbing contract is 2/3 and the
probability that he will not get an
electrical contract is 5/9.If the
probability of getting at least one
contract is 4/5,what is the probability
that he will get both?
4. A card is drawn from a pack of 52 cards.
Find the prob. of getting a king or a heart
or a red card?

19. 5. Two dice are tossed.find the probability of
getting an ‘even number on first die or a
total of 8’.
6. The prob. That a student passes a Physics
test is 2/3 and the probability that he
passes both a Physics and English test is
14/45.The probability that he passes at
least one test is 4/5.What is the
probability he passes the English test?

20. Answers
1. 8/25,2/5
2. 0.03
3. 0.31
4. 7/13
5. 5/9
6. 4/9

21. Multiplication Theorem
If two Independent events occur simultaneously
P(A.B) = P(A).P(B)
OR
P(A Ç B)=P(A).P(B)
OR
P(A AND B)=P(A).P(B)
If A & B are Dependent events
P(A/B):Conditional
Prob. of event ‘A’
given that B has
already occurred.
P(A Ç B)= P(B).P(A/B) ; P(B)>0
P(A Ç B)= P(A).P(B/A) ; P(A)>0

22. More results
For two Independent events A&B
P(A Ç B)= P(A).P(B)
 For three Independent events A,B&C
P(A Ç B)= P(A).P(B)
P(A ÇC)= P(A).P(C)
P(B ÇC)= P(B).P(C)
P(A Ç B Ç C)= P(A).P(B).P(C)
 For two mutually exclusive events A&B,
A Ç B=Æ AND P(A Ç B) =0

23. Results contd..
 Probability of the complementary event Ac
of A is given by
P(Ac)=1-P(A)
 Demorgan’s Law
(AÇB)c = Ac È Bc
(AÈB)c = Ac Ç Bc

24. Questions for practice
1. An MBA applies for job in two firms X and
Y.The probability of his being selected in
firm X is 0.7 and being rejected at Y is
0.5. What is the probability that he will
selected in one of the firms?
2. Probability that A can solve a problem is
4/5, B can solve it is 2/3 and C can solve it
is 3/7.If all of them try independently,
find the probability that the problem is
solved.

25. 3. A bag contains 5 White and 3 Black
Balls.Two balls are drawn at random
one after the other without
replacement.Find the probability
that both balls drawn are black.
4. Find the probability of drawing a
queen,a king and a jack in that order
from a pack of cards in three
consecutive draws,the card drawn is
not been replaced?

26. 5. The odds against manager X settling
the wage dispute with the workers
are 8:6 and odds in favour of
Manager Y settling the same
dispute are 14:16.
(i) What is the chance that neither
settles the dispute, if they both
try,independently of each other?
(ii) What is the probability that dispute
will be settled?

27. 6. A box contains 3 red and 7 white balls.one
ball is drawn at random and in its place a
ball of other color is put in the box.Now
one ball is drawn at random from the
box.Find the probability that it is red.
7. A husband and wife appear in an
interview for two vacancies in the same
post. The probability of husband’s
selection is 1/7 and that of wife’s
selection is 1/5. What is the probability
that(i) both will be selected
ii) only one will be selected
iii)none be selected

28. Answers
1. 0.5
2. 101/1105
3. 3/28
4. .00048
5. 32/105,73/105
6. 0.34
7. .029,0.286,0.686