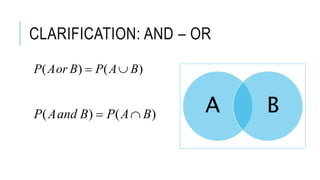
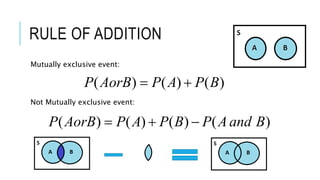
This document provides an overview of probability concepts including: - Basic terms like probability, sample space, events, mutually exclusive and independent events - How to calculate probability using the formula of number of favorable outcomes divided by total possible outcomes - Examples of calculating probability of events like rolling dice, drawing cards, balls from a bag - Rules of probability like addition, multiplication and Bayes' theorem - Examples of calculating probability of independent and dependent events using coins, balls from bags, light bulbs from machines - Concepts of permutations and combinations

1. PROBABILITY Presented by:
Savi Arora

2. BASIC TERMS
Probability: Measure if likeliness than an event will
occur.
Sample Space: Set of all possible outcomes.
Event: Any subset of any outcomes of any
experiment.
Mutually exclusive event: Event which cannot occur
together.
Dependent and Independent events.

3. PROBABILITY MANTRA
outcomepossibleofnoTotal
outcomefavourableofNo
EP )(

4. TODAY WE WILL PLAY WITH
Coins
Dice
Cards
&
A bag full of colorful balls.

5. PRACTICE – 1
A dice is thrown, find probability
P(even no) =
P(no less than 3) =
P(not 3) =
In a deck of 52 cards
P(ace) =
P(red card) =
P(face card) =

6. CLARIFICATION: AND – OR
)()( BAPBorAP 
)()( BAPBandAP  A B

7. RULE OF ADDITION
Mutually exclusive event:
Not Mutually exclusive event:
)()()( BPAPAorBP 
)()()()( BandAPBPAPAorBP 

8. PRACTICE – 2
A Dice is thrown once:
P( 2 or 3) =
P(multiple of 2 or multiple of 3) =
In Deck of 52 cards
P(red or face) =
One ball drawn: Bag contains – 10 Red, 15 Yellow, 25
Green
P( Yellow or Green) =

9. RULE OF MULTIPLICATION
Independent Events:
Dependent Event:
)()()( BPAPBandAP 
)|()()( ABPAPBandAP 
)|()()( BAPBPBandAP Or

10. PRACTICE – 3
Bag contains – 10 Red, 15 Yellow, 25 Green
Two balls drawn (with replacement):
P(1st Red, 2nd Yellow) =
P(Both Red) =
P(One Red, one Yellow) =
Two balls drawn (without replacement):
P(1st Red, 2nd Yellow) =
P(Both Red) =
P(One Red, one Yellow) =

11. COIN
Two unbiased coins are tossed simultaneously:
P(one head) =
P(atleast one head) =
P(No head) =
P(one Head one Tail) =

12. COIN
Three unbiased coins are tossed simultaneously:
P(two head) =
P(at least two head) =
P(at most two head) =
P(All head) =

13. COIN
Four or More Coins are tossed??
You need Binomial for that.

14. PERMUTATION & COMBINATION
Permutation: “one or more elements of a set where order does
matter”
Combination: “one or more elements of a set where order does not
matter”
For e.g.: Take 3 Letters – ABCPermutation of 2 of
these letter: 3P2 = 6
AB BA
AC CA
BC CB
Combination of 2 of
these letter: 3C2 = 3
AB
AC
BC
Now Take 4 : Letter – ABCD
And write Permutation & Combination of 3 of th

15. P&C
Permutation
Combination
3 𝐶2 =
3!
3 − 2 ! 2!
= 3n 𝐶 𝑟 =
𝑛!
𝑛 − 𝑟 ! 𝑟!
3 𝑃2 =
3!
3−2 !
= 6
n 𝑃 𝑟 =
𝑛!
𝑛 − 𝑟 !
*We will focus majorly on COMBINATIO

16. PRACTICE – 4
Bag is Back : 10 Red, 15 Yellow, 25 Green
Three bolls drawn at random, find:
P(each different color) =
P(2 red 1 green) =
P(exactly 2 green) =
P(at least 2 green) =
P(at most 2 green) =

17. PRACTICE – 4
Bag is Back : 10 Red, 15 Yellow, 25 Green
Two draws of three balls each are drawn at random (with
replacement)
P(1st three Red, 2nd three yellow) =
P(all different color, all different color) =
P(one draws three red, other draws three yellow) =
*Wanna try without replacement??

18. BAYES’ THEOREM
What is the probability of outcome A given that outcome B has
already occurred. i.e. P(A|B)
)'().'|()().|(
)().|(
)|(
APABPAPABP
APABP
BAP


n.,...2,1,=k,
)B|P(A×)P(B
)B|P(A×)P(B
=A)|P(B
1
ii
ik
k

n
i
Believe me! You don’t need to remember this, if you Still go with your Probability Mantra a

19. ILLUSTRATION
Late
BusCar Train
P(train)train)|P(lateP(bus)bus)|P(lateP(car)car)|P(late
P(car)car)|P(late
late)|P(car



P(Car) = P(Bus) = P(Train) = 1/3
P(late|car) = 1/6
P(late|bus) = 1/5
P(late|train) = 1/4
Given that You are Late, what is the probability that you travelled by car??

20. PRACTICE – 5
A bulb is manufactured in one of the three machines X,Y,Z.
The machines produce in capacity: X – 30%, Y – 30%, Z – 40%.
Probability of bulb found defective in machine X – 10%, Y – 15%,
Z – 20%.
A bulb is drawn at random and is found to be defective.
What is the probability that the bulb was produced in Machine
Y??

21. THANK YOU
Queries are welcomed.