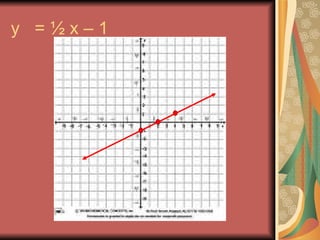
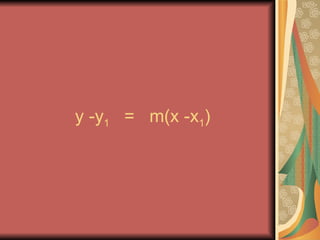This document summarizes how to write linear equations in standard form and point-slope form. It explains how to write an equation in standard form by moving the x term to the same side as the y term. It then explains how to use the point-slope form, which is y-y1=m(x-x1), to write an equation when given a point and the slope. It walks through examples of using point-slope form to write equations for lines with slopes of 3 and 1/2 when given a point.

1. Standard Form and Point Slope Form

5. Point Slope Form Find an equation with one set of coordinates and the slope.

7. If y = mx + b, and then y – y 1 =m(x-x 1 ) this is done algebraically by multiplying both sides by (x 2 -x 1 )

8. Related formula

9. y -y 1 = m(x -x 1 )

16. y = ½ x – 1

18. Copyright D Dahlberg