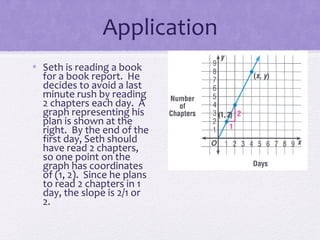
This document provides examples for writing linear equations in point-slope form and standard form. It defines point-slope form as y - y1 = m(x - x1) and standard form as Ax + By = C. Several examples are worked through, showing how to write an equation in point-slope form given a point and slope, and then how to convert it to standard form by multiplying terms to eliminate fractions and arranging the variables as x then y. The key steps of finding slope from two points, writing the equation in point-slope form, and then converting it to standard form without fractions are demonstrated.

1. 6.3 Write Linear Equations in
Point-Slope Form
6.4 Write Linear Equations in
Standard forms

2. Objective
• Write a linear equation in standard form given the
coordinates of a point on the line and the slope of the line.
• Write a linear equation in standard form given the
coordinates of two points on a line.

3. Application
• Seth is reading a book
for a book report. He
decides to avoid a last
minute rush by reading
2 chapters each day. A
graph representing his
plan is shown at the
right. By the end of the
first day, Seth should
have read 2 chapters,
so one point on the
graph has coordinates
of (1, 2). Since he plans
to read 2 chapters in 1
day, the slope is 2/1 or
2.

4. Application
y2 − y1
m=
x2 − x1
y−2
=2
x −1
Slope formula
Substitute values
y − 2 = 2( x − 1)
Multiply each side by x-1
This linear equation is said to be in point-slope form.

5. Point-Slope Form
• For a given point (x1, y1) on a non-vertical line with
slope m, the point-slope form of a linear equation
is as follows:
y – y1 = m(x – x1)
In general, you can write an equation in point-slope
form for the graph of any non-vertical line. If you
know the slope of a line and the coordinates of
one point on the line, you can write an equation of
the line.

6. Ex. 1: Write the point-slope form of an equation of the line
passing through (2, -4) and having a slope of 2/3.
y – y1 = m(x – x1)
Point-Slope form
2
y − (−4) = (x − 2) Substitute known values.
3
2
y + 4 = (x − 2) Simplify
3
An equation of the
line is:
2
y + 4 = ( x − 2)
3

7. Ex. 2: Write the point-slope form of an equation of the line
that passes through the points (7, 2) and (2,12)

8. Standard Form
• Any linear equation can be expressed in the form Ax +
By = C where A, B, and C are integers and A and B are
not both zero. This is called standard form. An
equation that is written in point-slope form can be
written in standard form.
• Rules for Standard Form:
• Standard form is Ax + By = C, with the following
conditions:
1) No fractions
2) A is not negative (it can be zero, but it can't be
negative).
By the way, "integer" means no fractions, no decimals.
Just clean whole numbers (or their negatives).

9. 3
)
Ex. 2: Write y + 4 = 4 ( x − 2in standard form.
3
y + 4 = ( x − 2)
4
Given
4(y + 4) = 3(x – 2)
Multiply by 4 to get rid of the fraction.
4y + 16 = 3x – 6
Distributive property
4y = 3x – 22
Subtract 16 from both sides
4y – 3x= – 22
Subtract 3x from both sides
– 3x + 4y = – 22
Format x before y

10. Ex. 3: Write the standard form of an equation of the
line passing through (5, 4), -2/3
2
y − 4 = − ( x − 5) Given
3
3(y - 4) = -2(x – 5)
Multiply by 3 to get rid of the fraction.
3y – 12 = -2x +10
Distributive property
3y = -2x +22
Add 12 to both sides
3y + 2x= 22
Add 2x to both sides
2x + 3y = 22
Format x before y

11. Ex. 4: Write the standard form of an equation of
the line passing through (-6, -3), -1/2
1
y +3 = − ( x + 6)
2
Given
2(y +3) = -1(x +6)
Multiply by 2 to get rid of the fraction.
2y + 6 = -1x – 6
Distributive property
2y = -1x – 12
Subtract 6 from both sides
2y + 1x= -12
Subtract 1x from both sides
x + 2y = -12
Format x before y

12. Ex. 6: Write the standard form of an equation of the
line passing through (5, 4), (6, 3)
y2 − y1
m=
First find slope of the line.
x2 − x1
m=
3 − 4 −1
=
= −1
6−5 1
y − 4 = −1( x − 5)
y – 4 = -1x + 5
y = -1x + 9
y+x=9
x+y=9
Substitute values and solve for m.
Put into point-slope form for conversion into
Standard Form Ax + By = C
Distributive property
Add 4 to both sides.
Add 1x to both sides
Standard form requires x come before y.

13. Ex. 7: Write the standard form of an equation of the
line passing through (-5, 1), (6, -2)
y2 − y1
m=
First find slope of the line.
x2 − x1
m=
− 2 −1
−3 −3
=
=
6 − (−5) 6 + 5 11 Substitute values and solve for m.
y −1 = −
3
( x + 5)
11
11(y
Put into point-slope form for conversion into
Standard Form Ax + By = C
– 1) = -3(x + 5)
11y – 11 = -3x – 15
11y
11y
= -3x – 4
Multiply by 11 to get rid of fraction
Distributive property
Add 4 to both sides.
+ 3x = -4
3x + 11y = -4
Add 1x to both sides
Standard form requires x come before y.