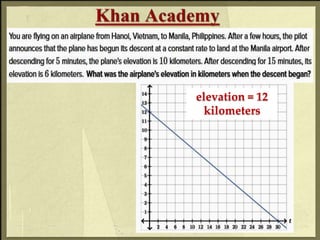
1. The document provides information on linear functions and how to determine if an equation represents a linear function. It discusses using standard form (Ax + By = C) to identify linear equations and determine intercepts. 2. The document contains examples of writing equations of lines given points and slopes in various forms. It discusses using point-slope form and converting between slope-intercept and standard form. 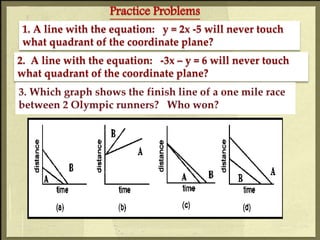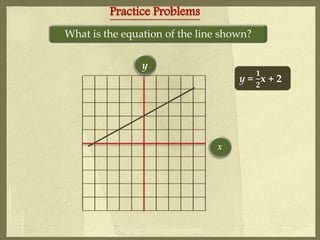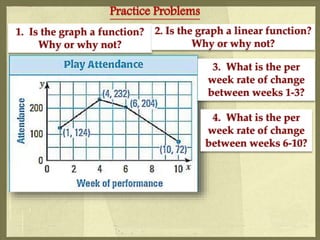3. The document provides practice problems determining if graphs are functions, whether equations represent lines, finding rates of change, intercepts, and writing equations in different forms. It aims to help students work with linear functions and equations.

1. 21
Today:

2. 1. - -3(8)
-2 + -(4)
3. Find the length & width:
2x + 10
x P = 68
2. Solve for x: rx + 9 = h
5
x = 5h -9
r
4. Solve: 2y + 2 < 11+ 3 < 8 + y

3. Interpreting Linear Functions
and Finding Intercepts

4. elevation = 12
kilometers

5. Draw a graph!
Draw a graph!
12 hours

6. • Linear Equations form straight lines. How do we
determine if an equation is linear?
It can be rewritten in the form: Ax + By = C
This is the Standard Form of a linear equation where:
a.) A and B are not both zero.
b.) The largest exponent is not greater than 1
Determine Whether the Equations are Linear:
1. 4 - 2y = 6x 2. -4/5x = -2 3. -6y + x = 5y - 2
Remember:
This is to determine whether an equation is linear
(forms a straight line) or not. The standard form is also
used to determine x and y intercepts.

7. Practice Questions:
1. From the table, determine the function, fill in the missing
values, and write the equation solving for y. f(x) =

8. Find the missing coordinate of a line with points (–2, R) and
(4, 6) and a slope of 3
2
Practice Questions:
If (a,2) is a point on the graph of 2x - 7y = 20, what is a?
R = -3
When to use the point-slope form of a line:
a. If all you have to work with is one point
on the line and the slope of the line
b. If all you have are two points on the line
Write the equation of a line passing through
the point (2,5) with a slope of -2

9. Practice Questions:
Write the standard form for the equation of the line
through the point (-2, 5) with a slope of 3.
Use the point-slope form, y – y1 = m(x – x1), with m = 3 and
(x1, y1) = (-2, 5). y – y1 = m(x – x1) Point-slope form
y – y1 = 3(x – x1) Let m = 3.
y – 5 = 3(x – (-2)) Let (x1, y1) = (-2, 5).
y – 5 = 3(x + 2) Simplify.
y = 3x + 11 Slope-intercept form
3x – y = - 11 Standard Form

10. Practice Questions:
Example: Write the equation of the line through the
points (4, 3) and (-2, 5).
y – y1 = m(x – x1) Point-slope form
Slope-intercept formy = - x + 13
3
1
3
2 15 – 3
-2 – 4
= -
6
= -
3
Calculate the slope.m =
Use m = - and the point (4, 3).y – 3 = - (x – 4)
1
3 3
1
Find the x-intercept of the line with slope of 2 and
passing through the points (-1, 2) and (0,4)

11. Find the equation of the line that has a slope of 𝟑 and a y-intercept of
-1. Graph the line and write the equation in both slope-intercept and
standard forms with integers only for the standard form.
The only information you have is the slope
𝟑
𝟒
, and a point on the
line, (1,2). Use the correct equation & graph the line. Then write
the equation in standard form with integers only.
You begin with the point-slope formula,
which becomes the slope-intercept form.
Use the slope-intercept to graph.
To put the equation in
standard form, you
can do this...
What if:

12. Practice Problems

13. Practice Problems
Standard Form,
No fractions

14. 1. A line with the equation: y = 2x -5 will never touch
what quadrant of the coordinate plane?
2. A line with the equation: -3x – y = 6 will never touch
what quadrant of the coordinate plane?
Practice Problems

15. x
y
What is the equation of the line shown?
Practice Problems
y =
𝟏
𝟐
x + 2

16. 1. Is the graph a function?
Why or why not?
2. Is the graph a linear function?
Why or why not?
3. What is the per
week rate of change
between weeks 1-3?
4. What is the per
week rate of change
between weeks 6-10?
Practice Problems

17. Class Work 2.12;
Show All Work

18. Practice Problems: