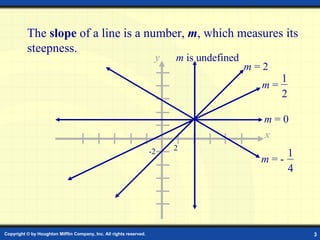
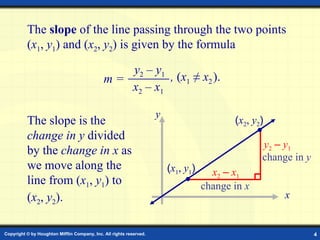
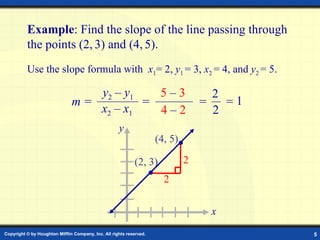
This document discusses key concepts related to linear equations in two variables including: 1. Linear equations can be written in the form ax + by = c and are graphed as lines. 2. The slope of a line measures its steepness and is calculated using the slope formula. 3. Linear equations can be written in slope-intercept form y = mx + b or point-slope form y - y1 = m(x - x1) to graph the line. 4. Parallel lines have the same slope while perpendicular lines have slopes that are negative reciprocals.

1. Linear Equations in Two Variables Digital Lesson

2. Linear Equations Equations of the form ax + by = c are called linear equations in two variables . The point (0,4) is the y -intercept . The point (6,0) is the x -intercept . x y 2 -2 This is the graph of the equation 2 x + 3 y = 12. (0,4) (6,0)

3. Slope of a Line The slope of a line is a number, m , which measures its steepness. m = 0 m = 2 m is undefined y x 2 -2 m = 1 2 m = - 1 4

4. Slope Formula The slope of the line passing through the two points ( x 1 , y 1 ) and ( x 2 , y 2 ) is given by the formula The slope is the change in y divided by the change in x as we move along the line from ( x 1 , y 1 ) to ( x 2 , y 2 ). x y x 2 – x 1 y 2 – y 1 change in y change in x y 2 – y 1 x 2 – x 1 m = , ( x 1 ≠ x 2 ). ( x 1 , y 1 ) ( x 2 , y 2 )

5. Example: Find Slope Example : Find the slope of the line passing through the points (2 , 3) and (4, 5). Use the slope formula with x 1 = 2 , y 1 = 3 , x 2 = 4 , and y 2 = 5 . 2 2 (2, 3) (4, 5) y 2 – y 1 x 2 – x 1 m = 5 – 3 4 – 2 = = 2 2 = 1 x y

6. Slope-Intercept Form A linear equation written in the form y = mx + b is in slope-intercept form . To graph an equation in slope-intercept form : 1. Write the equation in the form y = mx + b. Identify m and b . The slope is m and the y-intercept is (0, b ). 2. Plot the y -intercept (0, b ). 3. Starting at the y -intercept, find another point on the line using the slope. 4. Draw the line through (0, b ) and the point located using the slope.

7. Example: y = mx + b 1 Example : Graph the line y = 2 x – 4. 2. Plot the y -intercept, (0, - 4). The equation y = 2 x – 4 is in the slope-intercept form. So, m = 2 and b = - 4. 3. The slope is 2. The point (1, -2) is also on the line. 4. Start at the point (0, 4). Count 1 unit to the right and 2 units up to locate a second point on the line. 2 5. Draw the line through (0, 4) and (1, -2). 1 = change in y change in x m = 2 x y (0, - 4) (1, -2)

8. Point-Slope Form A linear equation written in the form y – y 1 = m ( x – x 1 ) is in point-slope form . The graph of this equation is a line with slope m passing through the point ( x 1 , y 1 ) . Example : The graph of the equation y – 3 = - ( x – 4) is a line of slope m = - passing through the point (4, 3). 1 2 1 2 (4, 3) m = - 1 2 x y 4 4 8 8

9. Example: Point-Slope Form Example : Write the slope-intercept form for the equation of the line through the point (-2, 5) with a slope of 3. Use the point-slope form, y – y 1 = m ( x – x 1 ) , with m = 3 and ( x 1 , y 1 ) = (-2, 5). y – y 1 = m ( x – x 1 ) Point-slope form y – y 1 = 3 ( x – x 1 ) Let m = 3. y – 5 = 3 ( x – ( -2 )) Let ( x 1 , y 1 ) = (-2, 5) . y – 5 = 3( x + 2) Simplify. y = 3 x + 11 Slope-intercept form

10. Example: Slope-Intercept Form Example : Write the slope-intercept form for the equation of the line through the points (4, 3) and (-2, 5). y – y 1 = m ( x – x 1 ) Point-slope form Slope-intercept form y = - x + 13 3 1 3 2 1 5 – 3 -2 – 4 = - 6 = - 3 Calculate the slope. m = Use m = - and the point (4, 3). y – 3 = - ( x – 4 ) 1 3

11. Example: Parallel Lines Two lines are parallel if they have the same slope. If the lines have slopes m 1 and m 2 , then the lines are parallel whenever m 1 = m 2 . Example : The lines y = 2 x – 3 and y = 2 x + 4 have slopes m 1 = 2 and m 2 = 2. The lines are parallel. x y y = 2 x + 4 (0, 4) y = 2 x – 3 (0, -3)

12. Example: Perpendicular Lines Two lines are perpendicular if their slopes are negative reciprocals of each other. If two lines have slopes m 1 and m 2 , then the lines are perpendicular whenever The lines are perpendicular. or m 1 m 2 = -1. y = 3 x – 1 (0, 4) (0, -1) 1 m 1 m 2 = - x y y = - x + 4 1 3 Example : The lines y = 3 x – 1 and y = - x + 4 have slopes m 1 = 3 and m 2 = - . 1 3 1 3