Downloaded 62 times
Uploaded byr3h1na
Relations and Functions
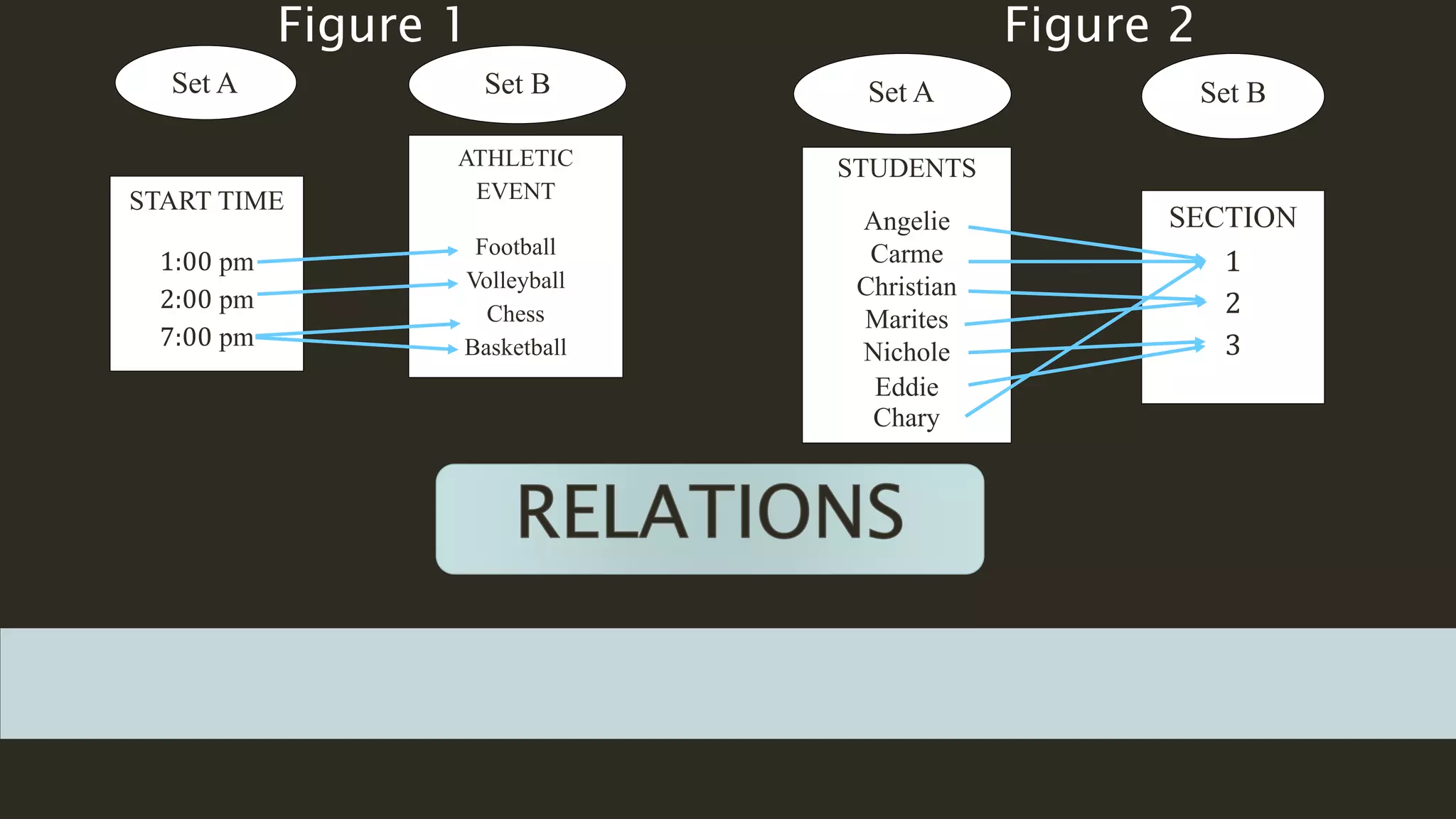
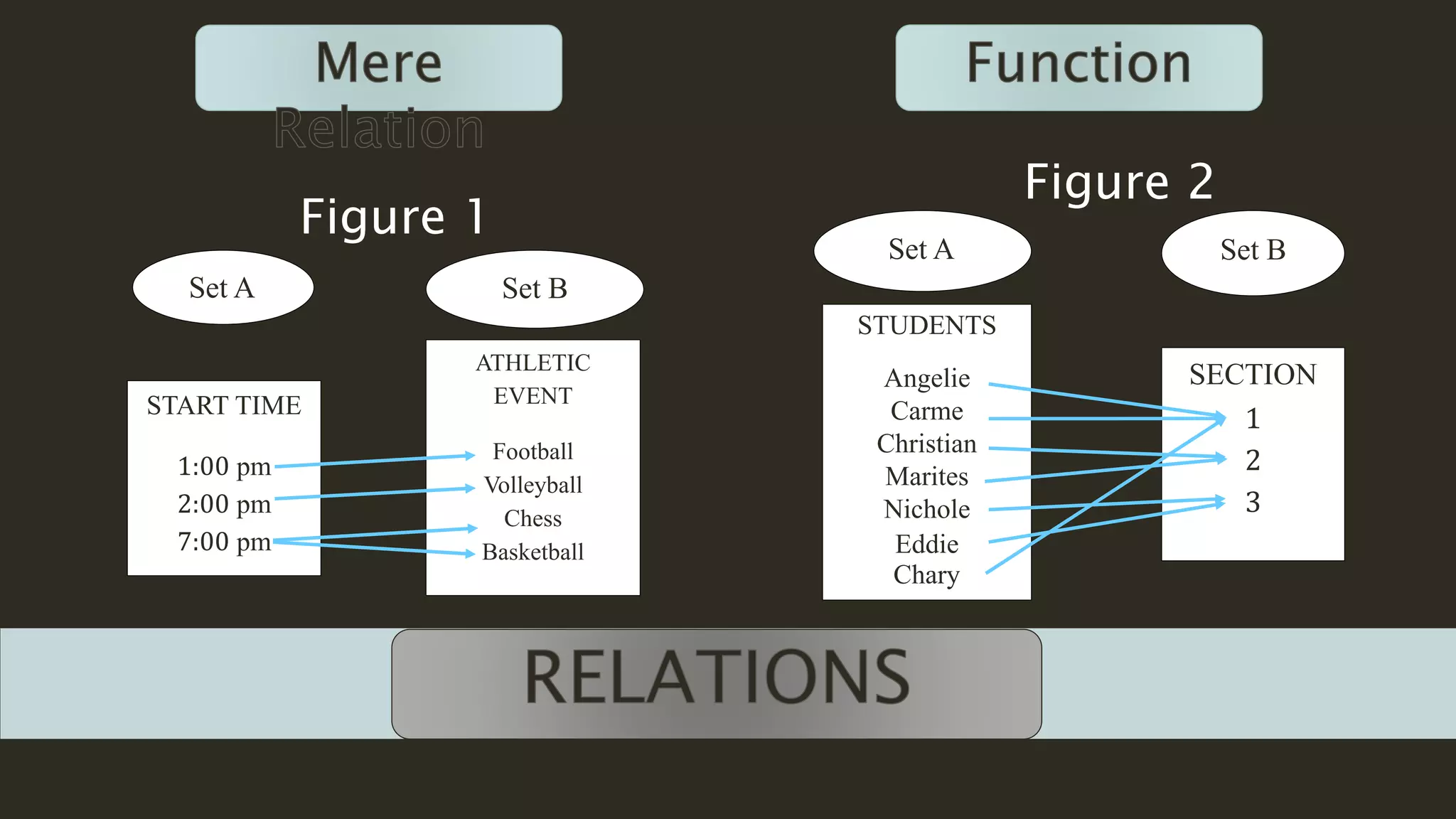
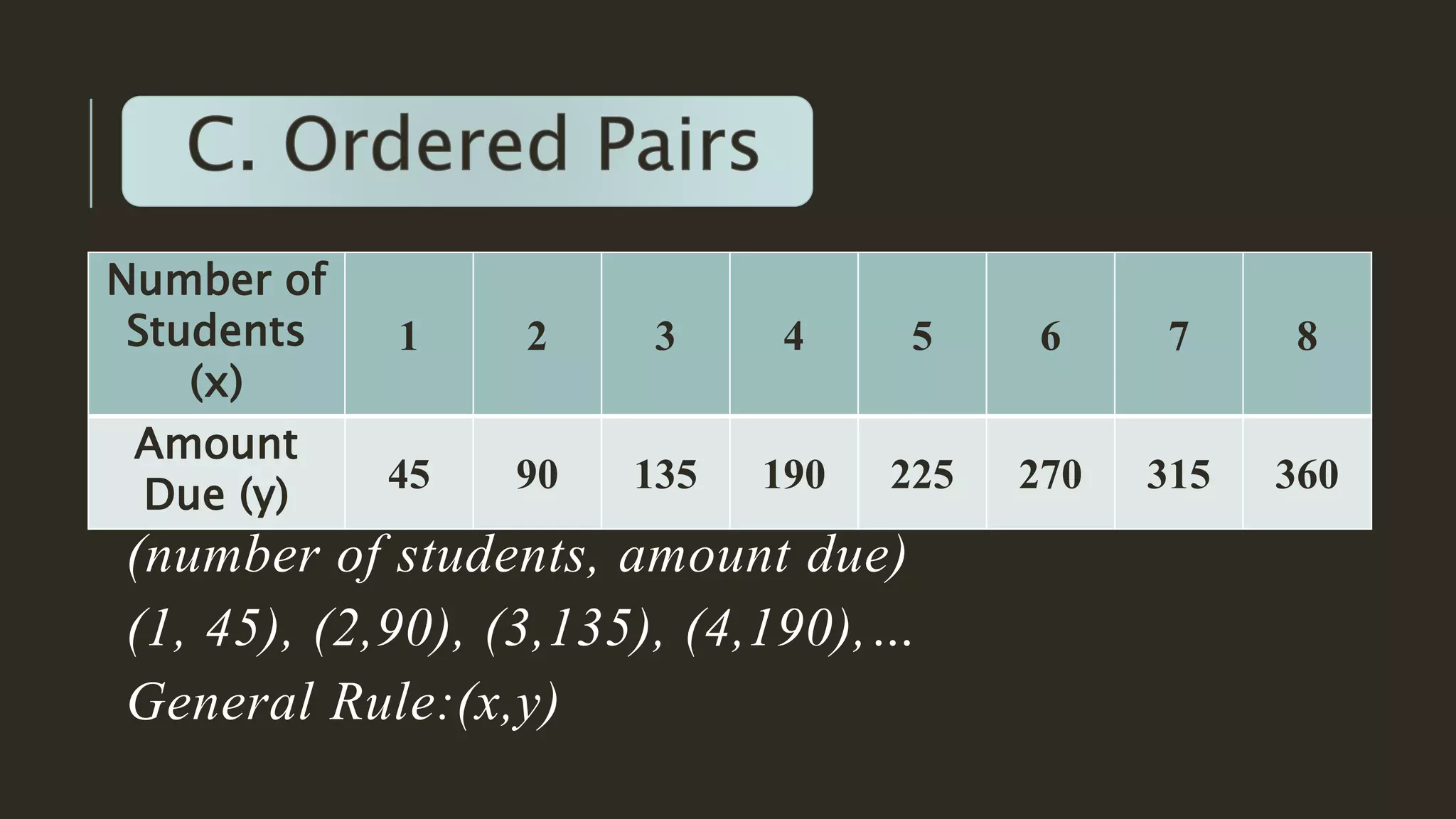
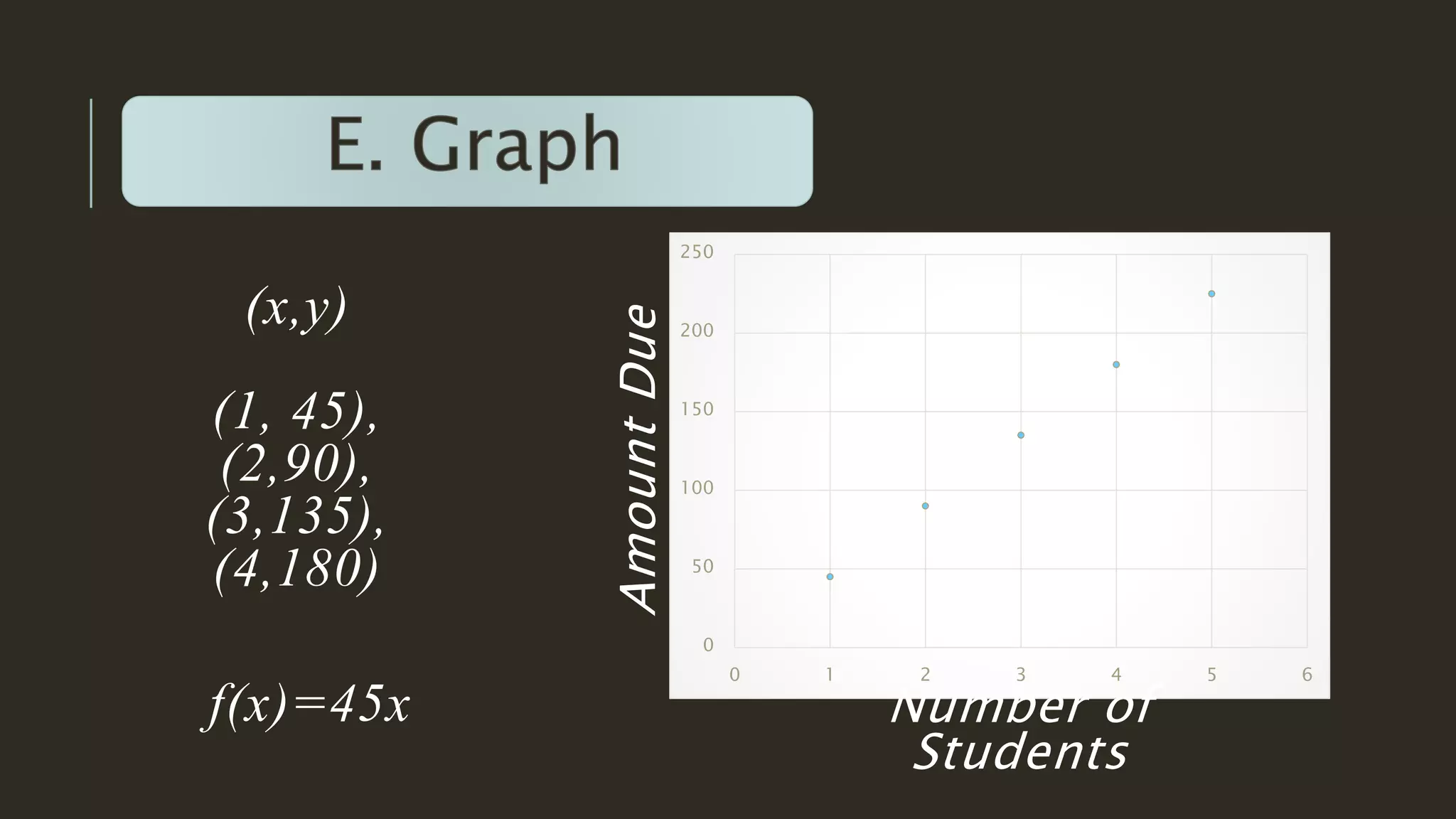
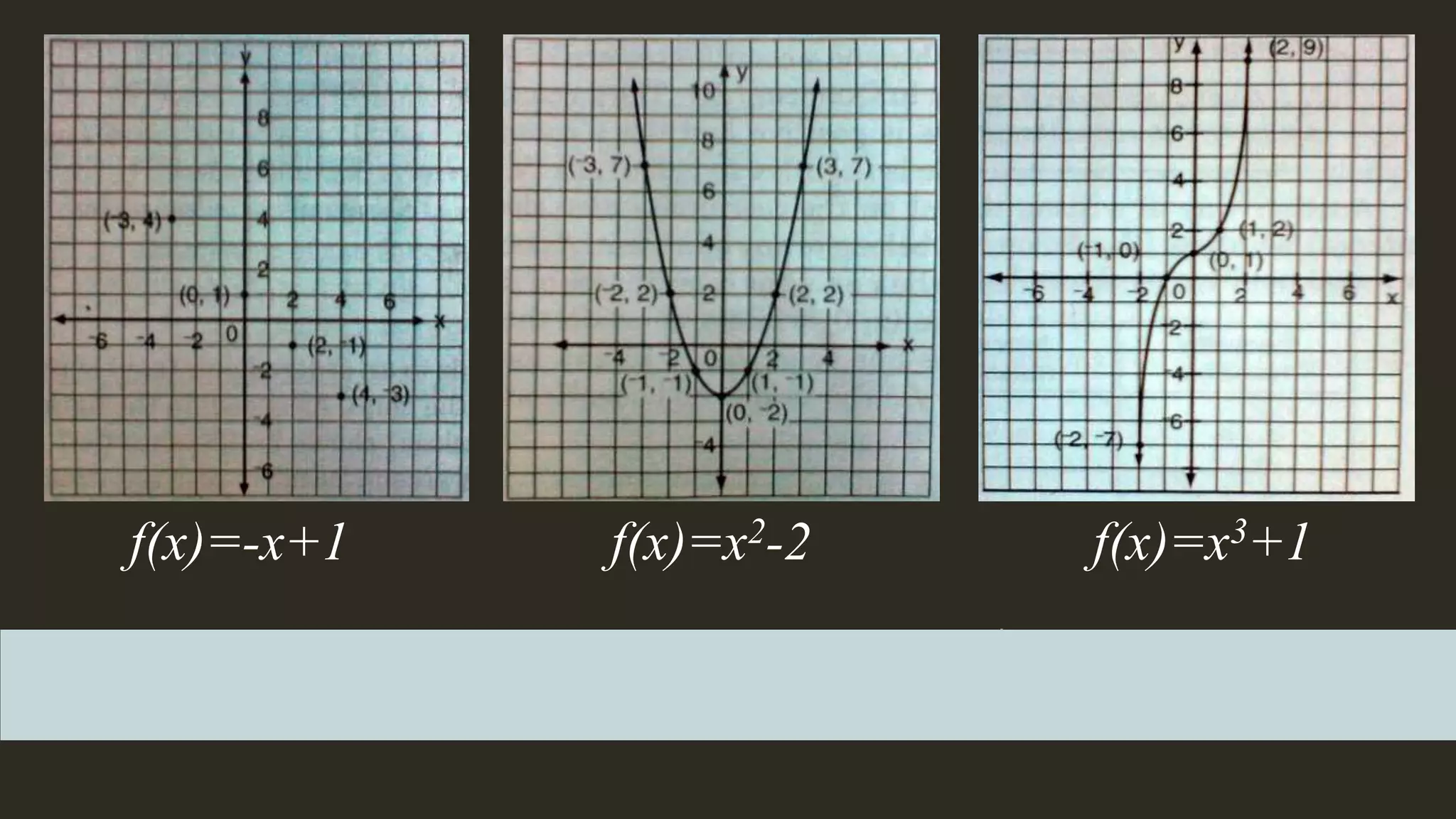
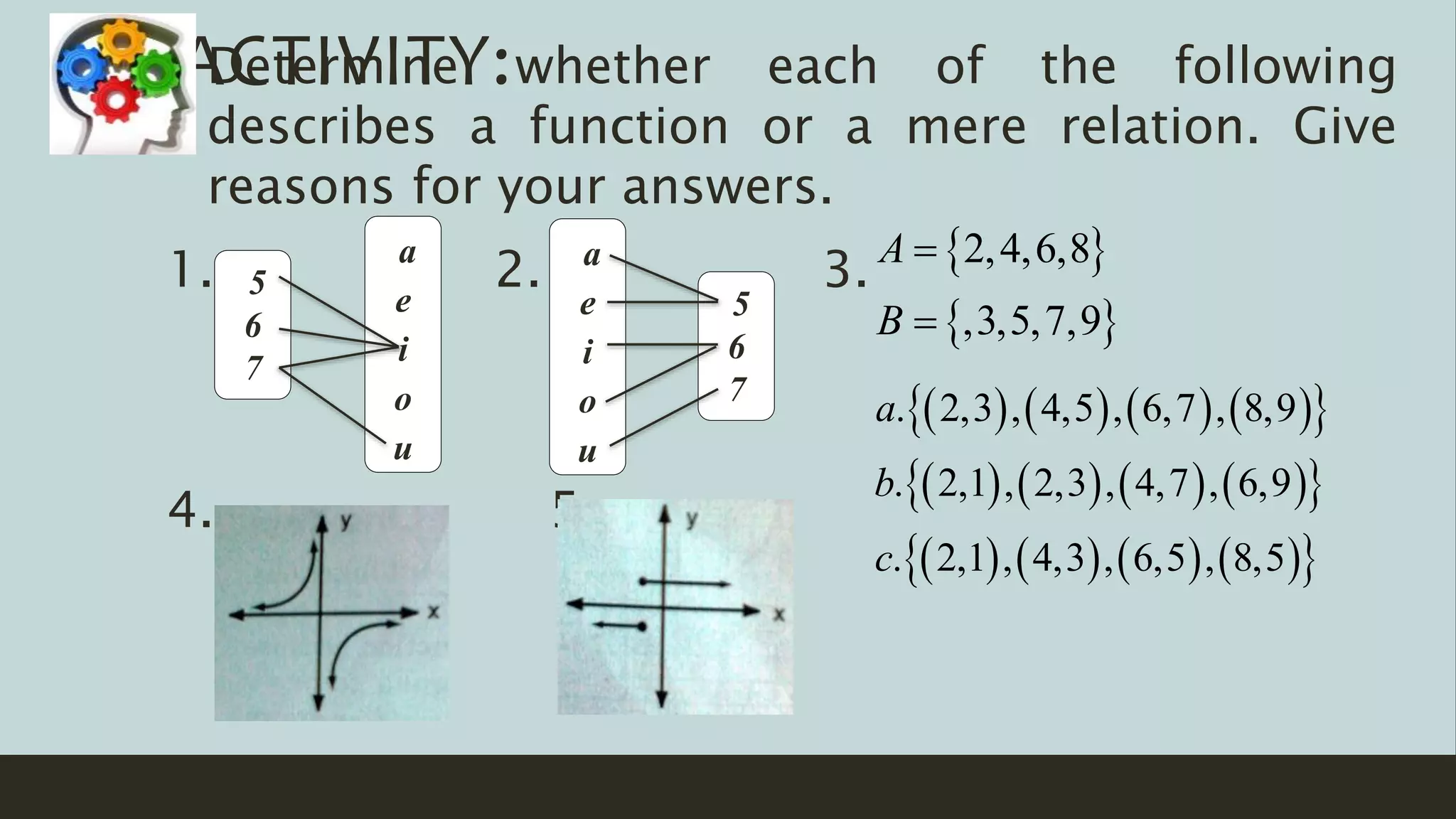
This document discusses functions and relations. It begins by defining a relation as a correspondence between two sets where each element in the first set corresponds to at least one element in the second set. It then defines a function as a special type of relation where each element in the first set corresponds to exactly one element in the second set. The document provides examples of functions defined using ordered pairs, tables, and algebraic rules. It also discusses how to graph functions and determine whether a set of ordered pairs represents a function or merely a relation. Students are assigned to write a short reflection on what they learned about functions and any difficulties understanding parts of the lesson.
More Related Content
Similar to Relations and Functions
Relations and Functions
- 1. RIGEN V. MAALAMBSED-Math 3 Relations and Functions
- 2. Learning Objectives: a. Distinguishfunction from mere relations. b. Describe functions using different methods. c. Discuss the importance of building a strong and positive relationship with the people around you.
- 3. START TIME 1:00 pm 2:00pm 7:00 pm Set A ATHLETIC EVENT Football Volleyball Chess Basketball Set B Figure 1 STUDENTS Angelie Carme Christian Marites Nichole Eddie Chary Set A SECTION 1 2 3 Set B Figure 2
- 4. A relation isa correspondence between two sets where each element in the first set, called the domain, corresponds to at least one element in the second set, called the range. DEFINITION:
- 5. START TIME 1:00 pm 2:00pm 7:00 pm Set A ATHLETIC EVENT Football Volleyball Chess Basketball Set B Figure 1 STUDENTS Angelie Carme Christian Marites Nichole Eddie Chary Set A SECTION 1 2 3 Set B Figure 2
- 6. A function isa relation in which each element in the domain corresponds to exactly one or unique element in the range. DEFINITION:
- 7. SUBJECTS Trigonometry Algebra Chemistry Geometry Physics Domain CALL NO. 510 512 513 516 530 Range Figure 3 APPLIANCE TurboBoiler Microwave Oven Refrigerator Washing Machine TV Set Domain SALE PRICE P8, 000 P12, 000 P14, 000 P16, 000 P18, 000 Range Figure 4
- 8. Main characteristics ofa function: 1. Each element in the domain is matched with exactly one, unique element in the range. 2. Two or more elements in the domain may be matched with the same element in the range. 3. Some elements in the range may not be matched with any element in the domain. REMEMBER
- 9.
- 10. SUBJECTS Trigonometry Algebra Chemistry Geometry Physics Domain CALL NO. 510 512 513 516 530 Range Figure 3 APPLIANCE TurboBoiler Microwave Oven Refrigerator Washing Machine TV Set Domain SALE PRICE P8, 000 P12, 000 P14, 000 P16, 000 P18, 000 Range Figure 4
- 11. A school canteensells lunch for P45. To facilitate the payments and avoid inaccuracy in computation, the student manager prepared a table to which she can refer when receiving payments. Number of Students (x) 1 2 3 4 5 6 7 8 Amount Due (y) 45 90 135 190 225 270 315 360
- 12. (1, 45), (2,90),(3,135), (4,190),… Number of Students (x) 1 2 3 4 5 6 7 8 Amount Due (y) 45 90 135 190 225 270 315 360 (number of students, amount due) General Rule:(x,y)
- 13. (1, 45), (2,90),(3,135), (4,180),…(x,y) 45=45(1) 90=45(2) 135=45(3) 180=45(4) General Rule: y=45x or f(x)=45x
- 14. (x,y) (1, 45), (2,90), (3,135), (4,180) f(x)=45x 0 50 100 150 200 250 0 12 3 4 5 6 Number of Students AmountDue
- 15. To sketch thegraph of a function, set the ordered pairs in a table, plot the points in the coordinate plane and connect them, with a smooth curve if necessary. Then, name the graph. REMEMBER
- 16.
- 17. A set ofpoints in a coordinate plane is the graph of a function if and only if no vertical line intersects the graph at more than one point. If any x-value corresponds to more than one y-value, then y is not a function of x. REMEMBER This graph is not a graph of a function.
- 18. Determine whether eachof the following describes a function or a mere relation. Give reasons for your answers. ACTIVITY: 5 6 7 a e i o u 5 6 7 a e i o u 1. 2. 3. 4. 5. 2,4,6,8 ,3,5,7,9 A B . 2,3 , 4,5 , 6,7 , 8,9 . 2,1 , 2,3 , 4,7 , 6,9 . 2,1 , 4,3 , 6,5 , 8,5 a b c
- 19. In a shortbond paper, make a 2- paragraph reflection paper of what you have learned in this topic and which part of the lesson you find difficulty in understanding. Pass it on Thursday, November 12, 2015. ASSIGNMENT:
Editor's Notes
- #4 Observe Figure 1 and figure 2 closely, what have you notice? What is their common feature? There is a correspondence from set A to B. And this correspondence is called .. RELATIONS Again, what is a relation?
- #6 Look at the digrams closely. A while back you have notice that their common feature is the correspondence from A to B. Now, do you see any difference between Figure 1 and Figure 2? What are those? This type of relation is called a function. So how do you define functions ____?
- #7 We can deduce that a function is more restrictive tan a mere relation because in a mere relation, the domain corresponds to at least (take note) at least one element in the range, whereas in functions..
- #8 More examples of a function. What have you noticed in figure3? How about in figure 4? To how many elements in the range did the domain corresponds to?
- #11 More examples of a function. What have you noticed in figure3? How about in figure 4? To how many elements in the range did the domain corresponds to?
- #12 For the next methods, I want you to refer to this problem. Do you see The rule for the relation is: multiply P45 by the number of students or . What makes it a function is that, each element in the first set (No. of Students) is matched with a unique element in the second set (Amount Due). a pattern?
- #13 Now, think of the pairs of numbers in the table as , then as ordered pairs and in general as .
- #14 From the ordered pairs, the relationships can be expressed as follows:
- #15 Using the equation y=45x and the values obtained in the previous table, the function can be represented as graph. The graph (of a function) provides a geometric picture of the way one quantity changes with respect to another quantity. In other words, relationships between quantities (variables) can be illustrated by means of lines and curves in any xy planewhich is commonly known as the the Cartesian plane, named after the French mathematician Rene Descartes (1596-1650). It is formed by two real number lines intersecting in right angles.
- #17 Illustrative Example: Not all represent a function. Given the graph of any equation, if a vertical line that can be drawn intersects the graph at no more than one point, then the equation defines as a function of . This is called the vertical line test.
- #18 Why you think that this graph is not a graph of a function? Here is a reminder.
- #19 In reality, we also have different functions in the family and in the society. And it is inevitable to be at odds with someone or develop a conflict with somebody. Did you ever experience having a misunderstanding with someone? How does it feel? What did you do to resolve the issue? How imssportant is it to build a strong and positive relationship with the people around you?