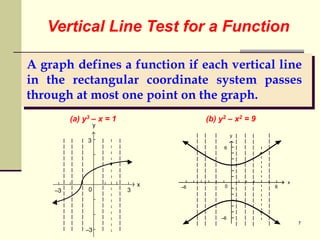
The document defines key terms related to functions including domain, range, and the relationship between independent and dependent variables. It provides examples of functions represented as sets of ordered pairs, equations, graphs, and tables. It discusses the vertical line test for determining if a relation represents a function. It also explains function notation and how to evaluate functions by substituting values for the independent variable.

1. Summary
1

2. Domain is the set of all permissible values of
the independent variable
Range is the set of all permissible values of the
dependent variable.
Relations: Domain, Range, and Rule
Permissible values of a variable
will not make the denominator zero
will not make the radicand of even
index negative

3. Functions
3

4. Functions
Definition Function
A function f from A to B is a relation from
A to B where to each , there
corresponds exactly one such that
A
a
B
b
  .
, f
b
a 
A function can also be defined as a set of
ordered pairs in which no two ordered
pairs have the same first component but
different second components. 4

5. SOME EXAMPLES OF FUNCTIONS
 Functions as set of
ordered pairs
f = {(1,1),(3,5),(4,6),(8,9)}
g = {(1,0),(2,0),(-1,5)}
 Functions as equations
 Functions as graphs
f(x) = x2 + 1
g(x) = 4 - 5x
 Functions as table of
values
No. of eggs
(x)x
Price of
breakfast
(y)
1 P10.00
2 P18.00
3 P22.00
5

6. For each relation, determine if it is a function.
r1= {(1,3),(2,5),(3,8),(4,10)}
r2 = {(-1,0),(2,-3),(.5,1),( 2/3,1/2)}
r3 = {(x,y)| y= 2x-5}
r4 = {(x,y)| y= x2}
r5 = {(x,y)| y > x-3}
Functions
Yes
Yes
Yes
Yes
No












 1
4
9
)
,
(
2
2
y
x
y
x
6
r No
6

7. x
y
3
–3
3
–3
0
x
y
6
–6
6
–6
0
A graph defines a function if each vertical line
in the rectangular coordinate system passes
through at most one point on the graph.
Vertical Line Test for a Function
(b) y2 – x2 = 9
(a) y3 – x = 1
7

8. Vertical Line Test for a Function
Which of the following graphs represent a
function?
x
y
x
y
x
y
x
y
Yes Yes
No No
8

9. 9
Which of the following mapping diagrams
represent functions?
Yes Yes No

10. 1. The following data were collected from members of
a college pre-calculus class.
Is the set of ordered pairs (x,y) a function?
TIME TO THINK
x
Height
y
Weight
72 in. 180 lb
60 in. 204 lb
60 in. 120 lb
63 in. 145 lb
70 in. 184 lb
a)
10

11. 2. The following data were collected from members of
a college pre-calculus class.
Is the set of ordered pairs (x,y) a function?
TIME TO THINK
b) x
year of graduation
y
number of graduates
2005 2
2006 12
2007 18
2008 7
2009 1
11

12. Suppose you’re given the equation
 f(x) should be read “f of x “, NOT “f times x”.
 f is the name of the function; it’s not a
number.
 x is the input value or independent variable.
 f(x) is the value of the function f at the
number x.
Function Notation
.
4
3
)
( 
 x
x
f
12

13. What does mean?
Suppose you’re given the equation
We may replace f(x) by y. That is, f(x) = y
which means that the value of the function is the
y value.
Function Notation
.
4
3
)
( 
 x
x
f
  10
2 
f
The value of f when x = 2 is 10.
13

14. Interpretation of f(x)
14

15. Evaluating a function
15

16. Evaluating a function
Evaluate the following functions at x = 1.5
16
𝑎. 𝑓(𝑥) = 2𝑥 + 1
𝑏. 𝑞(𝑥) = 𝑥2
− 2𝑥 + 2
𝑓 1.5 = 2 1.5 + 1
𝑓(1.5) = 4
𝑞(1.5) = 1.5 2
− 2(1.5) + 2
𝑞(1.5) = 1.25

17. Evaluating a function
Evaluate the following functions at x = 1.5
17
𝑐. 𝑔(𝑥) = 𝑥 + 1
𝑑. 𝑟(𝑥) =
2𝑥 + 1
𝑥 − 1
𝑔(1.5) = 1.5 + 1
𝑔(1.5) = 2.5
𝑟(1.5) =
2(1.5) + 1
1.5 − 1
𝑟(1.5) = 8

18. Evaluating a function
Evaluate the function 𝑓(3𝑥 − 1)
Evaluate the function 𝑞(3𝑥 + 3)
18
𝑒. 𝑓(𝑥) = 2𝑥 + 1
𝑓. 𝑞(𝑥) = 𝑥2
− 2𝑥 + 2
𝑓 3𝑥 − 1 = 2 3𝑥 − 1 + 1
𝑓 3𝑥 − 1 = 6𝑥 − 1
𝑞(3𝑥 + 3) = 3𝑥 + 3 2
− 2(3𝑥 + 3) + 2
𝑞 3𝑥 + 3 = 4𝑥2
+ 8𝑥 + 5

19. 1. Given 𝑓 𝑥 = 𝑥 − 2. Find the following
values:
𝑎. 𝑓 0
𝑏. 𝑓 3
𝑐. 𝑓 −1
𝑑. 𝑓 𝜋
𝑒. 𝑓 𝑥 + 1
19
TIME TO THINK

20. 2. Given 𝑓 𝑥 =
4
𝑥
. Find the following values:
𝑎. 𝑓 1
𝑏. 𝑓 2
𝑐. 𝑓 −1
𝑑. 𝑓 2
𝑒. 𝑓
1
𝑥
20
TIME TO THINK