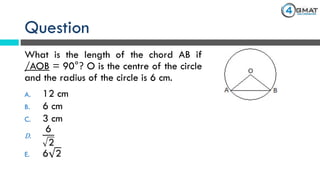
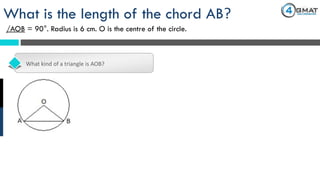
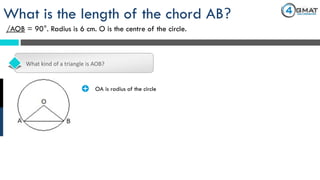
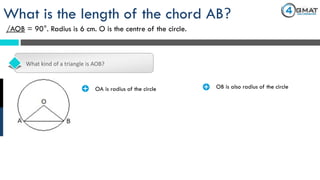
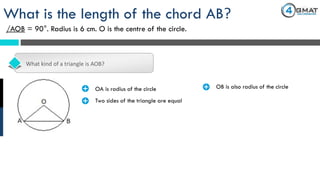
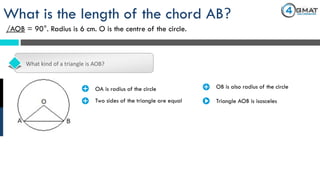
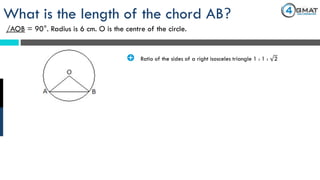
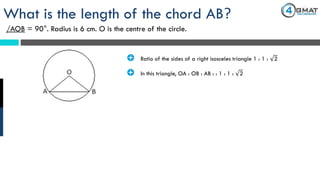
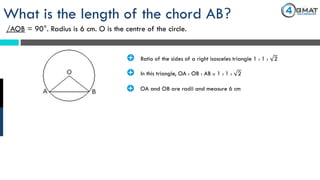
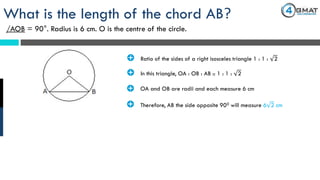
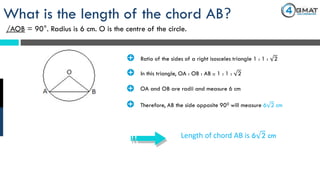
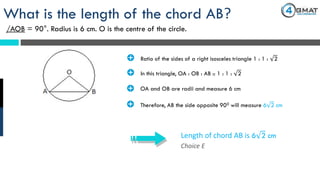
The document presents a GMAT quantitative reasoning problem involving geometry, specifically focusing on finding the length of a chord (AB) in a circle given that the angle AOB is 90° and the radius is 6 cm. It explains the properties of triangle AOB, determining it is a right isosceles triangle, leading to the conclusion that the length of the chord AB is 6√2 cm. The document also includes promotional content for GMAT preparation services.

1. GMAT QUANTITATIVE REASONING
GEOMETRY - CIRCLES
PROBLEM SOLVING
Diagnostic Test

2. Question
What is the length of the chord AB if
/AOB = 90°? O is the centre of the circle
and the radius of the circle is 6 cm.
A. 12 cm
B. 6 cm
C. 3 cm
D.
6
2
E. 6 2

3. What is the approach?

4. What is the length of the chord AB?
/AOB = 90°. Radius is 6 cm. O is the centre of the circle.
01 What kind of a triangle is AOB?

5. What is the length of the chord AB?
/AOB = 90°. Radius is 6 cm. O is the centre of the circle.
01 What kind of a triangle is AOB?
02 Is it any special triangle?

6. What is the length of the chord AB?
/AOB = 90°. Radius is 6 cm. O is the centre of the circle.
01 What kind of a triangle is AOB?
02 Is it any special triangle?
03 If so apply any relevant property of the special triangle and find the answer.

7. Part 1
What kind of a triangle is AOB?

8. What kind of a triangle is AOB?
What is the length of the chord AB?
/AOB = 90°. Radius is 6 cm. O is the centre of the circle.

9. What kind of a triangle is AOB?
What is the length of the chord AB?
/AOB = 90°. Radius is 6 cm. O is the centre of the circle.
· OA is radius of the circle

10. What kind of a triangle is AOB?
What is the length of the chord AB?
/AOB = 90°. Radius is 6 cm. O is the centre of the circle.
· OA is radius of the circle · OB is also radius of the circle

11. What kind of a triangle is AOB?
What is the length of the chord AB?
/AOB = 90°. Radius is 6 cm. O is the centre of the circle.
· OA is radius of the circle · OB is also radius of the circle
Two sides of the triangle are equal·

12. What kind of a triangle is AOB?
What is the length of the chord AB?
/AOB = 90°. Radius is 6 cm. O is the centre of the circle.
· OA is radius of the circle · OB is also radius of the circle
Two sides of the triangle are equal· Triangle AOB is isosceles

13. What kind of a triangle is AOB?
What is the length of the chord AB?
/AOB = 90°. Radius is 6 cm. O is the centre of the circle.
· OA is radius of the circle · OB is also radius of the circle
Two sides of the triangle are equal· Triangle AOB is isosceles
/AOB = 90°. So, AOB is a right
triangle

14. What kind of a triangle is AOB?
What is the length of the chord AB?
/AOB = 90°. Radius is 6 cm. O is the centre of the circle.
· OA is radius of the circle · OB is also radius of the circle
Two sides of the triangle are equal· Triangle AOB is isosceles
/AOB = 90°. So, AOB is a right
triangle
Therefore, AOB is a right isosceles
triangle

15. What kind of a triangle is AOB?
Ratio of the sides of a right isosceles triangle
What is the length of the chord AB?
/AOB = 90°. Radius is 6 cm. O is the centre of the circle.
· OA is radius of the circle · OB is also radius of the circle
Two sides of the triangle are equal· Triangle AOB is isosceles
/AOB = 90°. So, AOB is a right
triangle
Therefore, AOB is a right isosceles
triangle

16. What kind of a triangle is AOB?
Ratio of the sides of a right isosceles triangle
What is the length of the chord AB?
/AOB = 90°. Radius is 6 cm. O is the centre of the circle.
· OA is radius of the circle · OB is also radius of the circle
Two sides of the triangle are equal· Triangle AOB is isosceles
/AOB = 90°. So, AOB is a right
triangle
Therefore, AOB is a right isosceles
triangle
Sides opposite 450 – 450 – 900 are in the ratio
1 : 1 : 2

17. Part 2
Compute the length of chord AB

18. What is the length of the chord AB?
/AOB = 90°. Radius is 6 cm. O is the centre of the circle.
· Ratio of the sides of a right isosceles triangle 1 : 1 : 2

19. What is the length of the chord AB?
/AOB = 90°. Radius is 6 cm. O is the centre of the circle.
· Ratio of the sides of a right isosceles triangle 1 : 1 : 2
· In this triangle, OA : OB : AB : : 1 : 1 : 2

20. What is the length of the chord AB?
/AOB = 90°. Radius is 6 cm. O is the centre of the circle.
· Ratio of the sides of a right isosceles triangle 1 : 1 : 2
· In this triangle, OA : OB : AB :: 1 : 1 : 2
· OA and OB are radii and measure 6 cm

21. What is the length of the chord AB?
/AOB = 90°. Radius is 6 cm. O is the centre of the circle.
· Ratio of the sides of a right isosceles triangle 1 : 1 : 2
· In this triangle, OA : OB : AB :: 1 : 1 : 2
· OA and OB are radii and each measure 6 cm
· Therefore, AB the side opposite 900 will measure 6 2 cm

22. Length of chord AB is 6 2 cm
What is the length of the chord AB?
/AOB = 90°. Radius is 6 cm. O is the centre of the circle.
· Ratio of the sides of a right isosceles triangle 1 : 1 : 2
· In this triangle, OA : OB : AB :: 1 : 1 : 2
· OA and OB are radii and measure 6 cm
· Therefore, AB the side opposite 900 will measure 6 2 cm

23. Choice E
Length of chord AB is 6 2 cm
What is the length of the chord AB?
/AOB = 90°. Radius is 6 cm. O is the centre of the circle.
· Ratio of the sides of a right isosceles triangle 1 : 1 : 2
· In this triangle, OA : OB : AB :: 1 : 1 : 2
· OA and OB are radii and measure 6 cm
· Therefore, AB the side opposite 900 will measure 6 2 cm

24. For GMAT Prep
Visit http://www.4gmat.com
GMAT Classes and GMAT Preparation
Send your comments / feedback to
info@4gmat.com

25. 4GMAT
We offer classroom training in Chennai and Bangalore
Tutors include GMAT 98%ilers, US B School
graduates and IIM graduates
Call us: +91 95000 48484
Mail us: info@4gmat.com