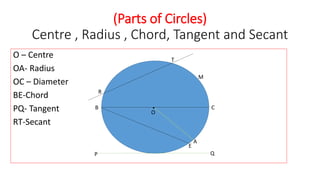
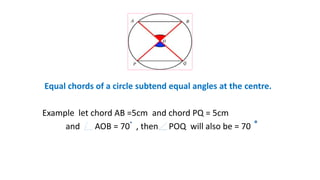
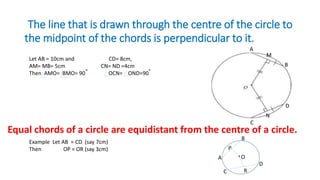
This document defines and describes key parts of a circle including the center, radius, diameter, chord, tangent, and secant. It explains that the radius is half the diameter and connects the center to points on the circle. The diameter passes through the center. A chord connects two points on the circle. A tangent touches at a single point while a secant intersects at two points. Equal chords subtend equal angles at the center and the line through the center to the chord midpoint is perpendicular to the chord. Equal chords are also equidistant from the center.

1. Identification
of Parts of
circle
properties
Related useful
results
Circles

2. (Parts of Circles)
Centre , Radius , Chord, Tangent and Secant
O – Centre
OA- Radius
OC – Diameter
BE-Chord
PQ- Tangent
RT-Secant
O
A
B C
M
P Q
E
R
T

3. RADIUS , DIAMETER, CHORD
RADIUS (OA)
Length of Radius is fixed for a given circle
Radius is half of diameter.
Radius joins centre of circle to any point on the circle.
DIAMETER (BC)
Length of Diameter is fixed for a given circle
Diameter is two times of Radius
Diameter always passes through centre. Example : if radius = 5 cm, diameter=5x2=10cm
maximum length of chord can not be greater then 10cm
CHORD (MN AND PR)
Length of Chord is not fixed. It joins any two points on the circle.
There can be infinite number of chords in a circle.
Longest chord is Diameter
o
A
B C
M N
RP
RADIUS , DIAMETER, CHORD

4. Tangent and Secant
• Tangent
• It touches the circle only at 1 single point.
• Angle between the tangent and radius is always 90
• Tangents are equal in length when it is drawn from a point
outside the circle.
( tangent touching at T(single point)
PQ =PR (both tangents will be equal in length
for example PQ and PR will be 7cm long)
• Secant
• It intersects the circle at two different points.
T
P
Q
R

5. Equal chords of a circle subtend equal angles at the centre.
Example let chord AB =5cm and chord PQ = 5cm
and AOB = 70 , then POQ will also be = 70

6. The line that is drawn through the centre of the circle to
the midpoint of the chords is perpendicular to it.
M
N
A
B
C
D
Let AB = 10cm and CD= 8cm,
AM= MB= 5cm CN= ND =4cm
Then AMO= BMO= 90 OCN= OND=90
Equal chords of a circle are equidistant from the centre of a circle.
A
B
D
C
O
P
R
Example Let AB = CD (say 7cm)
Then OP = OR (say 3cm)