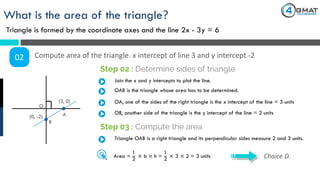
The document presents a diagnostic test question regarding the calculation of the area of a triangle formed by the coordinate axes and the line given by the equation 2x - 3y = 6. It explains the steps to determine the x and y intercepts, establish the sides of the triangle, and ultimately calculate the area, arriving at a final area of 3 square units. The document also includes promotional information about GMAT preparation classes.

1. GMAT QUANTITATIVE REASONING
COORDINATE GEOMETRY
PROBLEM SOLVING
Diagnostic Test

2. Question
What is the area of the triangle formed by the coordinate
axes and the line L whose equation is 2x - 3y = 6?
A. 6
B. 12
C. 13
D. 3
E. 7.5

3. Step 1
What kind of a triangle is formed?

4. What is the area of the triangle?
Triangle is formed by the coordinate axes and the line 2x - 3y = 6

5. What is the area of the triangle?
Triangle is formed by the coordinate axes and the line 2x - 3y = 6
The coordinate axes (x and y axes)
form sides of the triangle.
The triangle is a right triangle.

6. Step 2
Plot the line on the x-y plane; determine
sides of the triangle; compute area

7. What is the area of the triangle?
Triangle is formed by the coordinate axes and the line 2x - 3y = 6
02 Steps to compute area of the triangle

8. Compute x and y
intercepts using the
equation of the line.
x & y intercepts
01
What is the area of the triangle?
Triangle is formed by the coordinate axes and the line 2x - 3y = 6
02 Steps to compute area of the triangle

9. Compute x and y
intercepts using the
equation of the line.
Determine sides of
the triangle from x
and y intercepts
x & y intercepts Sides of triangle
01
02
What is the area of the triangle?
Triangle is formed by the coordinate axes and the line 2x - 3y = 6
02 Steps to compute area of the triangle

10. Compute x and y
intercepts using the
equation of the line.
Determine sides of
the triangle from x
and y intercepts
Using data on sides,
compute area of
triangle
x & y intercepts Sides of triangle Find area
01
02
03
What is the area of the triangle?
Triangle is formed by the coordinate axes and the line 2x - 3y = 6
02 Steps to compute area of the triangle

11. What is the area of the triangle?
Triangle is formed by the coordinate axes and the line 2x - 3y = 6
02 Compute area of the triangle. Equation of the line is 2x – 3y = 6
Step 01 : Compute x and y intercepts

12. What is the area of the triangle?
Triangle is formed by the coordinate axes and the line 2x - 3y = 6
02 Compute area of the triangle. Equation of the line is 2x – 3y = 6
x-intercept is the point where the
line meets the x-axis. At that point,
the y coordinate is ‘0’ (zero)
Step 01 : Compute x and y intercepts

13. What is the area of the triangle?
Triangle is formed by the coordinate axes and the line 2x - 3y = 6
02 Compute area of the triangle. Equation of the line is 2x – 3y = 6
x-intercept is the point where the
line meets the x-axis. At that point,
the y coordinate is ‘0’ (zero)
Step 01 : Compute x and y intercepts
To determine x-intercept of a line, substitute y =
0 in the equation of the line.

14. What is the area of the triangle?
Triangle is formed by the coordinate axes and the line 2x - 3y = 6
02 Compute area of the triangle. Equation of the line is 2x – 3y = 6
x-intercept is the point where the
line meets the x-axis. At that point,
the y coordinate is ‘0’ (zero)
Step 01 : Compute x and y intercepts
To determine x-intercept of a line, substitute y =
0 in the equation of the line.
2x – 3(0) = 6 or x = 3. x-intercept of the line is 3

15. What is the area of the triangle?
Triangle is formed by the coordinate axes and the line 2x - 3y = 6
02 Compute area of the triangle. Equation of the line is 2x – 3y = 6
x-intercept is the point where the
line meets the x-axis. At that point,
the y coordinate is ‘0’ (zero)
Step 01 : Compute x and y intercepts
To determine x-intercept of a line, substitute y =
0 in the equation of the line.
2x – 3(0) = 6 or x = 3. x-intercept of the line is 3
y-intercept is the point where the
line meets the y-axis. At that point,
the x coordinate is ‘0’ (zero)

16. What is the area of the triangle?
Triangle is formed by the coordinate axes and the line 2x - 3y = 6
02 Compute area of the triangle. Equation of the line is 2x – 3y = 6
x-intercept is the point where the
line meets the x-axis. At that point,
the y coordinate is ‘0’ (zero)
Step 01 : Compute x and y intercepts
To determine x-intercept of a line, substitute y =
0 in the equation of the line.
2x – 3(0) = 6 or x = 3. x-intercept of the line is 3
y-intercept is the point where the
line meets the y-axis. At that point,
the x coordinate is ‘0’ (zero)
To determine y-intercept of a line, substitute x =
0 in the equation of the line.

17. What is the area of the triangle?
Triangle is formed by the coordinate axes and the line 2x - 3y = 6
02 Compute area of the triangle. Equation of the line is 2x – 3y = 6
x-intercept is the point where the
line meets the x-axis. At that point,
the y coordinate is ‘0’ (zero)
Step 01 : Compute x and y intercepts
To determine x-intercept of a line, substitute y =
0 in the equation of the line.
2x – 3(0) = 6 or x = 3. x-intercept of the line is 3
y-intercept is the point where the
line meets the y-axis. At that point,
the x coordinate is ‘0’ (zero)
To determine y-intercept of a line, substitute x =
0 in the equation of the line.
2(0) – 3y = 6 or y = -2. y-intercept of the line is -2

18. What is the area of the triangle?
Triangle is formed by the coordinate axes and the line 2x - 3y = 6
02 Compute area of the triangle. x intercept of line 3 and y intercept -2
Step 02 : Determine sides of triangle

19. What is the area of the triangle?
Triangle is formed by the coordinate axes and the line 2x - 3y = 6
02 Compute area of the triangle. x intercept of line 3 and y intercept -2
Step 02 : Determine sides of triangle
Join the x and y intercepts to plot the line.

20. What is the area of the triangle?
Triangle is formed by the coordinate axes and the line 2x - 3y = 6
02 Compute area of the triangle. x intercept of line 3 and y intercept -2
Step 02 : Determine sides of triangle
(3, 0)
Join the x and y intercepts to plot the line.

21. What is the area of the triangle?
Triangle is formed by the coordinate axes and the line 2x - 3y = 6
02 Compute area of the triangle. x intercept of line 3 and y intercept -2
Step 02 : Determine sides of triangle
(3, 0)
(0, -2)
Join the x and y intercepts to plot the line.

22. What is the area of the triangle?
Triangle is formed by the coordinate axes and the line 2x - 3y = 6
02 Compute area of the triangle. x intercept of line 3 and y intercept -2
Step 02 : Determine sides of triangle
(3, 0)
(0, -2)
Join the x and y intercepts to plot the line.

23. What is the area of the triangle?
Triangle is formed by the coordinate axes and the line 2x - 3y = 6
02 Compute area of the triangle. x intercept of line 3 and y intercept -2
Step 02 : Determine sides of triangle
(3, 0)
(0, -2)
Join the x and y intercepts to plot the line.
OAB is the triangle whose area has to be determined.
O
A
B

24. What is the area of the triangle?
Triangle is formed by the coordinate axes and the line 2x - 3y = 6
02 Compute area of the triangle. x intercept of line 3 and y intercept -2
Step 02 : Determine sides of triangle
(3, 0)
(0, -2)
Join the x and y intercepts to plot the line.
OAB is the triangle whose area has to be determined.
O
A
B
OA, one of the sides of the right triangle is the x intercept of the line = 3 units

25. What is the area of the triangle?
Triangle is formed by the coordinate axes and the line 2x - 3y = 6
02 Compute area of the triangle. x intercept of line 3 and y intercept -2
Step 02 : Determine sides of triangle
(3, 0)
(0, -2)
Join the x and y intercepts to plot the line.
OAB is the triangle whose area has to be determined.
O
A
B
OB, another side of the triangle is the y intercept of the line = 2 units
OA, one of the sides of the right triangle is the x intercept of the line = 3 units

26. What is the area of the triangle?
Triangle is formed by the coordinate axes and the line 2x - 3y = 6
02 Compute area of the triangle. x intercept of line 3 and y intercept -2
Step 02 : Determine sides of triangle
(3, 0)
(0, -2)
Join the x and y intercepts to plot the line.
OAB is the triangle whose area has to be determined.
O
A
B
OB, another side of the triangle is the y intercept of the line = 2 units
Step 03 : Compute the area
OA, one of the sides of the right triangle is the x intercept of the line = 3 units

27. What is the area of the triangle?
Triangle is formed by the coordinate axes and the line 2x - 3y = 6
02 Compute area of the triangle. x intercept of line 3 and y intercept -2
Step 02 : Determine sides of triangle
(3, 0)
(0, -2)
Join the x and y intercepts to plot the line.
OAB is the triangle whose area has to be determined.
O
A
B
OB, another side of the triangle is the y intercept of the line = 2 units
Step 03 : Compute the area
Triangle OAB is a right triangle and its perpendicular sides measure 2 and 3 units.
OA, one of the sides of the right triangle is the x intercept of the line = 3 units

28. What is the area of the triangle?
Triangle is formed by the coordinate axes and the line 2x - 3y = 6
02 Compute area of the triangle. x intercept of line 3 and y intercept -2
Step 02 : Determine sides of triangle
(3, 0)
(0, -2)
Join the x and y intercepts to plot the line.
OAB is the triangle whose area has to be determined.
O
A
B
OB, another side of the triangle is the y intercept of the line = 2 units
Step 03 : Compute the area
Triangle OAB is a right triangle and its perpendicular sides measure 2 and 3 units.
Area =
1
2
× b × h =
1
2
× 3 × 2 = 3 units
OA, one of the sides of the right triangle is the x intercept of the line = 3 units

29. What is the area of the triangle?
Triangle is formed by the coordinate axes and the line 2x - 3y = 6
02 Compute area of the triangle. x intercept of line 3 and y intercept -2
Step 02 : Determine sides of triangle
(3, 0)
(0, -2)
Join the x and y intercepts to plot the line.
OAB is the triangle whose area has to be determined.
O
A
B
OB, another side of the triangle is the y intercept of the line = 2 units
Step 03 : Compute the area
Triangle OAB is a right triangle and its perpendicular sides measure 2 and 3 units.
Area =
1
2
× b × h =
1
2
× 3 × 2 = 3 units Choice D.
OA, one of the sides of the right triangle is the x intercept of the line = 3 units

30. For GMAT Prep
Visit http://www.4gmat.com
GMAT Classes and GMAT Preparation
Send your comments / feedback to
info@4gmat.com

31. 4GMAT
We offer classroom training in Chennai and Bangalore
Tutors include GMAT 98%ilers, US B School
graduates and IIM graduates
Call us: +91 95000 48484
Mail us: info@4gmat.com