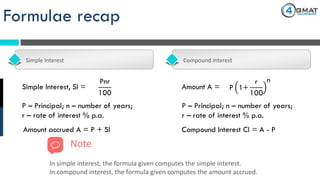
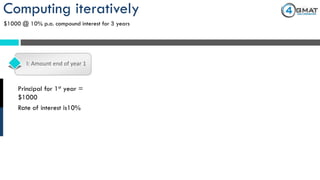
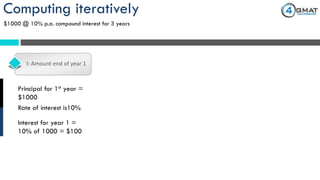
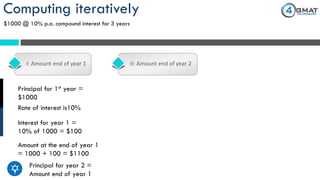
The document presents a problem-solving exercise involving simple and compound interest calculations based on Robin's investments of $1000 each in 12% simple interest and 10% compound interest for 3 years. At the end of the term, the simple interest earned is $360, while the compound interest amounts to $331, yielding a difference of $29 favoring the simple interest. The correct answer to the question posed is choice d, indicating how much more interest Robin received from his simple interest deposit compared to the compound interest one.

1. GMAT QUANTITATIVE REASONING
SIMPLE & COMPOUND
INTEREST
PROBLEM SOLVING
Diagnostic Test

2. Question
Robin invested $1000 in a 12% simple interest savings deposit for 3
years. He also invested an equal amount in a 10% compound interest
savings deposit for 3 years. At the end of 3 years, how much more
interest did he get from the simple interest deposit?
A. $31
B. $60
C. $39
D. $29
E. $390

3. Part 1
Simple & Compound Interest Formulae

4. Formulae recap
Simple Interest

5. Formulae recap
Simple Interest
Pnr
100
Simple Interest, SI =

6. Formulae recap
Simple Interest
Pnr
100
Simple Interest, SI =
P – Principal; n – number of years;
r – rate of interest % p.a.

7. Formulae recap
Simple Interest
Pnr
100
Simple Interest, SI =
Amount accrued A = P + SI
P – Principal; n – number of years;
r – rate of interest % p.a.

8. Formulae recap
Simple Interest Compound Interest
Pnr
100
Simple Interest, SI =
Amount accrued A = P + SI
P – Principal; n – number of years;
r – rate of interest % p.a.

9. Formulae recap
Simple Interest Compound Interest
Pnr
100
Simple Interest, SI =
Amount accrued A = P + SI
P – Principal; n – number of years;
r – rate of interest % p.a.
Amount A = P 1+
r
100
n

10. Formulae recap
Simple Interest Compound Interest
Pnr
100
Simple Interest, SI =
Amount accrued A = P + SI
P – Principal; n – number of years;
r – rate of interest % p.a.
Amount A = P 1+
r
100
n
P – Principal; n – number of years;
r – rate of interest % p.a.

11. Formulae recap
Simple Interest Compound Interest
Pnr
100
Simple Interest, SI =
Amount accrued A = P + SI
P – Principal; n – number of years;
r – rate of interest % p.a.
Amount A = P 1+
r
100
n
P – Principal; n – number of years;
r – rate of interest % p.a.
Compound Interest CI = A - P

12. Formulae recap
Simple Interest Compound Interest
Pnr
100
Simple Interest, SI =
Amount accrued A = P + SI
P – Principal; n – number of years;
r – rate of interest % p.a.
Amount A = P 1+
r
100
n
P – Principal; n – number of years;
r – rate of interest % p.a.
Compound Interest CI = A - P
Note
In simple interest, the formula given computes the simple interest.
In compound interest, the formula given computes the amount accrued.

13. Part 2
Compute simple and compound interest

14. At the end of 3 years, how much more interest did he
get from the simple interest deposit?
Step 1: Compute simple interest

15. $1000 in a 12% simple interest savings deposit for 3 years
At the end of 3 years, how much more interest did he
get from the simple interest deposit?
Step 1: Compute simple interest

16. $1000 in a 12% simple interest savings deposit for 3 years
Pnr
100
Simple Interest, SI =
At the end of 3 years, how much more interest did he
get from the simple interest deposit?
Step 1: Compute simple interest

17. $1000 in a 12% simple interest savings deposit for 3 years
Pnr
100
Simple Interest, SI =
At the end of 3 years, how much more interest did he
get from the simple interest deposit?
Step 1: Compute simple interest
Simple Interest, SI =

18. $1000 in a 12% simple interest savings deposit for 3 years
Pnr
100
Simple Interest, SI =
At the end of 3 years, how much more interest did he
get from the simple interest deposit?
Step 1: Compute simple interest
Simple Interest, SI = 1000×3×12
100

19. $1000 in a 12% simple interest savings deposit for 3 years
Pnr
100
Simple Interest, SI =
At the end of 3 years, how much more interest did he
get from the simple interest deposit?
Step 1: Compute simple interest
Simple Interest, SI = 1000×3×12
100
= $360

20. $1000 in a 12% simple interest savings deposit for 3 years
Pnr
100
Simple Interest, SI =
$360
Simple Interest
At the end of 3 years, how much more interest did he
get from the simple interest deposit?
Step 1: Compute simple interest
Simple Interest, SI = 1000×3×12
100
= $360

21. Step 2: Compute compound interest
At the end of 3 years, how much more interest did he
get from the simple interest deposit?

22. $1000 in a 10% compound interest savings deposit for 3 years
Step 2: Compute compound interest
At the end of 3 years, how much more interest did he
get from the simple interest deposit?

23. $1000 in a 10% compound interest savings deposit for 3 years
Amount A = P 1+
r
100
n
Step 2: Compute compound interest
At the end of 3 years, how much more interest did he
get from the simple interest deposit?

24. $1000 in a 10% compound interest savings deposit for 3 years
Amount A = P 1+
r
100
n
Step 2: Compute compound interest
At the end of 3 years, how much more interest did he
get from the simple interest deposit?
Amount A =

25. $1000 in a 10% compound interest savings deposit for 3 years
Amount A = P 1+
r
100
n
Step 2: Compute compound interest
At the end of 3 years, how much more interest did he
get from the simple interest deposit?
Amount A = 1000 1+
10
100
3

26. $1000 in a 10% compound interest savings deposit for 3 years
Amount A = P 1+
r
100
n
Step 2: Compute compound interest
At the end of 3 years, how much more interest did he
get from the simple interest deposit?
Amount A = 1000 1+
10
100
3
= 1000
100+10
100
3

27. $1000 in a 10% compound interest savings deposit for 3 years
Amount A = P 1+
r
100
n
Step 2: Compute compound interest
At the end of 3 years, how much more interest did he
get from the simple interest deposit?
Amount A = 1000 1+
10
100
3
= 1000
100+10
100
3
= 1000
110
100
3

28. $1000 in a 10% compound interest savings deposit for 3 years
Amount A = P 1+
r
100
n
Step 2: Compute compound interest
At the end of 3 years, how much more interest did he
get from the simple interest deposit?
Amount A = 1000 1+
10
100
3
= 1000
100+10
100
3
= 1000
110
100
3
= $1331

29. $1000 in a 10% compound interest savings deposit for 3 years
Amount A = P 1+
r
100
n
Step 2: Compute compound interest
At the end of 3 years, how much more interest did he
get from the simple interest deposit?
Amount A = 1000 1+
10
100
3
= 1000
100+10
100
3
= 1000
110
100
3
= $1331
Compound Interest CI = A - P

30. $1000 in a 10% compound interest savings deposit for 3 years
Amount A = P 1+
r
100
n
Step 2: Compute compound interest
At the end of 3 years, how much more interest did he
get from the simple interest deposit?
Amount A = 1000 1+
10
100
3
= 1000
100+10
100
3
= 1000
110
100
3
= $1331
Compound Interest CI = A - P = 1331 - 1000 = $331

31. $1000 in a 10% compound interest savings deposit for 3 years
Amount A = P 1+
r
100
n
$331
Compound Interest
Step 2: Compute compound interest
At the end of 3 years, how much more interest did he
get from the simple interest deposit?
Amount A = 1000 1+
10
100
3
= 1000
100+10
100
3
= 1000
110
100
3
= $1331
Compound Interest CI = A - P = 1331 - 1000 = $331

32. At the end of 3 years, how much more interest did he
get from the simple interest deposit?
Step 3: Compute the difference

33. At the end of 3 years, how much more interest did he
get from the simple interest deposit?
Step 3: Compute the difference
01 Simple interest = $360

34. At the end of 3 years, how much more interest did he
get from the simple interest deposit?
Step 3: Compute the difference
01 Simple interest = $360 02 Compound interest = $331

35. Difference = 360 – 331 = $29
At the end of 3 years, how much more interest did he
get from the simple interest deposit?
Step 3: Compute the difference
01 Simple interest = $360 02 Compound interest = $331

36. Correct Answer choice D.
Difference = 360 – 331 = $29
At the end of 3 years, how much more interest did he
get from the simple interest deposit?
Step 3: Compute the difference
01 Simple interest = $360 02 Compound interest = $331

37. Alternative Method to compute CI
Do not use formula

38. Computing iteratively
$1000 @ 10% p.a. compound interest for 3 years
I: Amount end of year 1

39. Computing iteratively
$1000 @ 10% p.a. compound interest for 3 years
I: Amount end of year 1
Principal for 1st year =
$1000
Rate of interest is10%

40. Computing iteratively
$1000 @ 10% p.a. compound interest for 3 years
I: Amount end of year 1
Principal for 1st year =
$1000
Rate of interest is10%
Interest for year 1 =
10% of 1000 = $100

41. Computing iteratively
$1000 @ 10% p.a. compound interest for 3 years
I: Amount end of year 1
Principal for 1st year =
$1000
Rate of interest is10%
Interest for year 1 =
10% of 1000 = $100
Amount at the end of year 1
= 1000 + 100 = $1100

42. Computing iteratively
$1000 @ 10% p.a. compound interest for 3 years
I: Amount end of year 1
Principal for 1st year =
$1000
Rate of interest is10%
Interest for year 1 =
10% of 1000 = $100
Amount at the end of year 1
= 1000 + 100 = $1100
Principal for year 2 =
Amount end of year 1

43. Computing iteratively
$1000 @ 10% p.a. compound interest for 3 years
I: Amount end of year 1 II: Amount end of year 2
Principal for 1st year =
$1000
Rate of interest is10%
Interest for year 1 =
10% of 1000 = $100
Amount at the end of year 1
= 1000 + 100 = $1100
Principal for year 2 =
Amount end of year 1

44. Computing iteratively
$1000 @ 10% p.a. compound interest for 3 years
I: Amount end of year 1 II: Amount end of year 2
Principal for 1st year =
$1000
Rate of interest is10%
Interest for year 1 =
10% of 1000 = $100
Amount at the end of year 1
= 1000 + 100 = $1100
Principal for year 2 =
Amount end of year 1
Principal for 2nd year =
$1100
Rate of interest is10%

45. Computing iteratively
$1000 @ 10% p.a. compound interest for 3 years
I: Amount end of year 1 II: Amount end of year 2
Principal for 1st year =
$1000
Rate of interest is10%
Interest for year 1 =
10% of 1000 = $100
Amount at the end of year 1
= 1000 + 100 = $1100
Principal for year 2 =
Amount end of year 1
Principal for 2nd year =
$1100
Rate of interest is10%
Interest for year 2 =
10% of 1100 = $110

46. Computing iteratively
$1000 @ 10% p.a. compound interest for 3 years
I: Amount end of year 1 II: Amount end of year 2
Principal for 1st year =
$1000
Rate of interest is10%
Interest for year 1 =
10% of 1000 = $100
Amount at the end of year 1
= 1000 + 100 = $1100
Principal for year 2 =
Amount end of year 1
Principal for 2nd year =
$1100
Rate of interest is10%
Interest for year 2 =
10% of 1100 = $110
Amount at the end of year 2
= 1100 + 110 = $1210

47. Computing iteratively
$1000 @ 10% p.a. compound interest for 3 years
I: Amount end of year 1 II: Amount end of year 2
Principal for 1st year =
$1000
Rate of interest is10%
Interest for year 1 =
10% of 1000 = $100
Amount at the end of year 1
= 1000 + 100 = $1100
Principal for year 2 =
Amount end of year 1
Principal for 2nd year =
$1100
Rate of interest is10%
Interest for year 2 =
10% of 1100 = $110
Amount at the end of year 2
= 1100 + 110 = $1210
Principal for year 3 =
Amount end of year 2

48. Computing iteratively
$1000 @ 10% p.a. compound interest for 3 years
I: Amount end of year 1 II: Amount end of year 2 III: Amount end of year 3
Principal for 1st year =
$1000
Rate of interest is10%
Interest for year 1 =
10% of 1000 = $100
Amount at the end of year 1
= 1000 + 100 = $1100
Principal for year 2 =
Amount end of year 1
Principal for 2nd year =
$1100
Rate of interest is10%
Interest for year 2 =
10% of 1100 = $110
Amount at the end of year 2
= 1100 + 110 = $1210
Principal for year 3 =
Amount end of year 2

49. Computing iteratively
$1000 @ 10% p.a. compound interest for 3 years
I: Amount end of year 1 II: Amount end of year 2 III: Amount end of year 3
Principal for 1st year =
$1000
Rate of interest is10%
Interest for year 1 =
10% of 1000 = $100
Amount at the end of year 1
= 1000 + 100 = $1100
Principal for year 2 =
Amount end of year 1
Principal for 2nd year =
$1100
Rate of interest is10%
Interest for year 2 =
10% of 1100 = $110
Amount at the end of year 2
= 1100 + 110 = $1210
Principal for year 3 =
Amount end of year 2
Principal for 3nd year =
$1210
Rate of interest is10%

50. Computing iteratively
$1000 @ 10% p.a. compound interest for 3 years
I: Amount end of year 1 II: Amount end of year 2 III: Amount end of year 3
Principal for 1st year =
$1000
Rate of interest is10%
Interest for year 1 =
10% of 1000 = $100
Amount at the end of year 1
= 1000 + 100 = $1100
Principal for year 2 =
Amount end of year 1
Principal for 2nd year =
$1100
Rate of interest is10%
Interest for year 2 =
10% of 1100 = $110
Amount at the end of year 2
= 1100 + 110 = $1210
Principal for year 3 =
Amount end of year 2
Principal for 3nd year =
$1210
Rate of interest is10%
Interest for year 3 =
10% of 1210 = $121

51. Computing iteratively
$1000 @ 10% p.a. compound interest for 3 years
I: Amount end of year 1 II: Amount end of year 2 III: Amount end of year 3
Principal for 1st year =
$1000
Rate of interest is10%
Interest for year 1 =
10% of 1000 = $100
Amount at the end of year 1
= 1000 + 100 = $1100
Principal for year 2 =
Amount end of year 1
Principal for 2nd year =
$1100
Rate of interest is10%
Interest for year 2 =
10% of 1100 = $110
Amount at the end of year 2
= 1100 + 110 = $1210
Principal for year 3 =
Amount end of year 2
Principal for 3nd year =
$1210
Rate of interest is10%
Interest for year 3 =
10% of 1210 = $121
Amount at the end of year 2
= 1210 + 121 = $1331

52. Computing iteratively
$1000 @ 10% p.a. compound interest for 3 years
I: Amount end of year 1 II: Amount end of year 2 III: Amount end of year 3
Principal for 1st year =
$1000
Rate of interest is10%
Interest for year 1 =
10% of 1000 = $100
Amount at the end of year 1
= 1000 + 100 = $1100
Principal for year 2 =
Amount end of year 1
Principal for 2nd year =
$1100
Rate of interest is10%
Interest for year 2 =
10% of 1100 = $110
Amount at the end of year 2
= 1100 + 110 = $1210
Principal for year 3 =
Amount end of year 2
Principal for 3nd year =
$1210
Rate of interest is10%
Interest for year 3 =
10% of 1210 = $121
Amount at the end of year 2
= 1210 + 121 = $1331
CI = 1331 – 1000 = $331

53. For GMAT Prep
Visit http://www.4gmat.com
GMAT Classes and GMAT Preparation
Send your comments / feedback to
info@4gmat.com

54. 4GMAT
We offer classroom training in Chennai and Bangalore
Tutors include GMAT 98%ilers, US B School
graduates and IIM graduates
Call us: +91 95000 48484
Mail us: info@4gmat.com