Embed presentation
Download to read offline
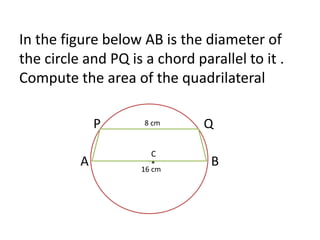

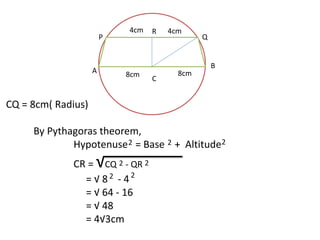
![Area of trapezium ABQP = ½ CR[PQ + AB]
= ½ 4 √3[8 + 16]
= 2 √3 × 24
= 48 √3 sq.cm](https://image.slidesharecdn.com/circles-140922042947-phpapp01/85/Circles-8-320.jpg)
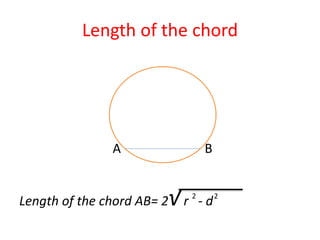
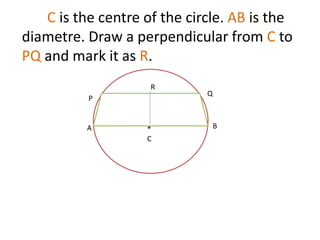
The document discusses calculating the area of a quadrilateral shape formed inside a circle. It defines the length of a chord in a circle and shows a diagram with a diameter AB and parallel chord PQ. It then finds the length of a perpendicular from the center C to the chord PQ, allowing the area of the quadrilateral PABQ to be determined using properties of chords, perpendiculars, radii, and the Pythagorean theorem.







![Area of trapezium ABQP = ½ CR[PQ + AB]
= ½ 4 √3[8 + 16]
= 2 √3 × 24
= 48 √3 sq.cm](https://image.slidesharecdn.com/circles-140922042947-phpapp01/85/Circles-8-320.jpg)