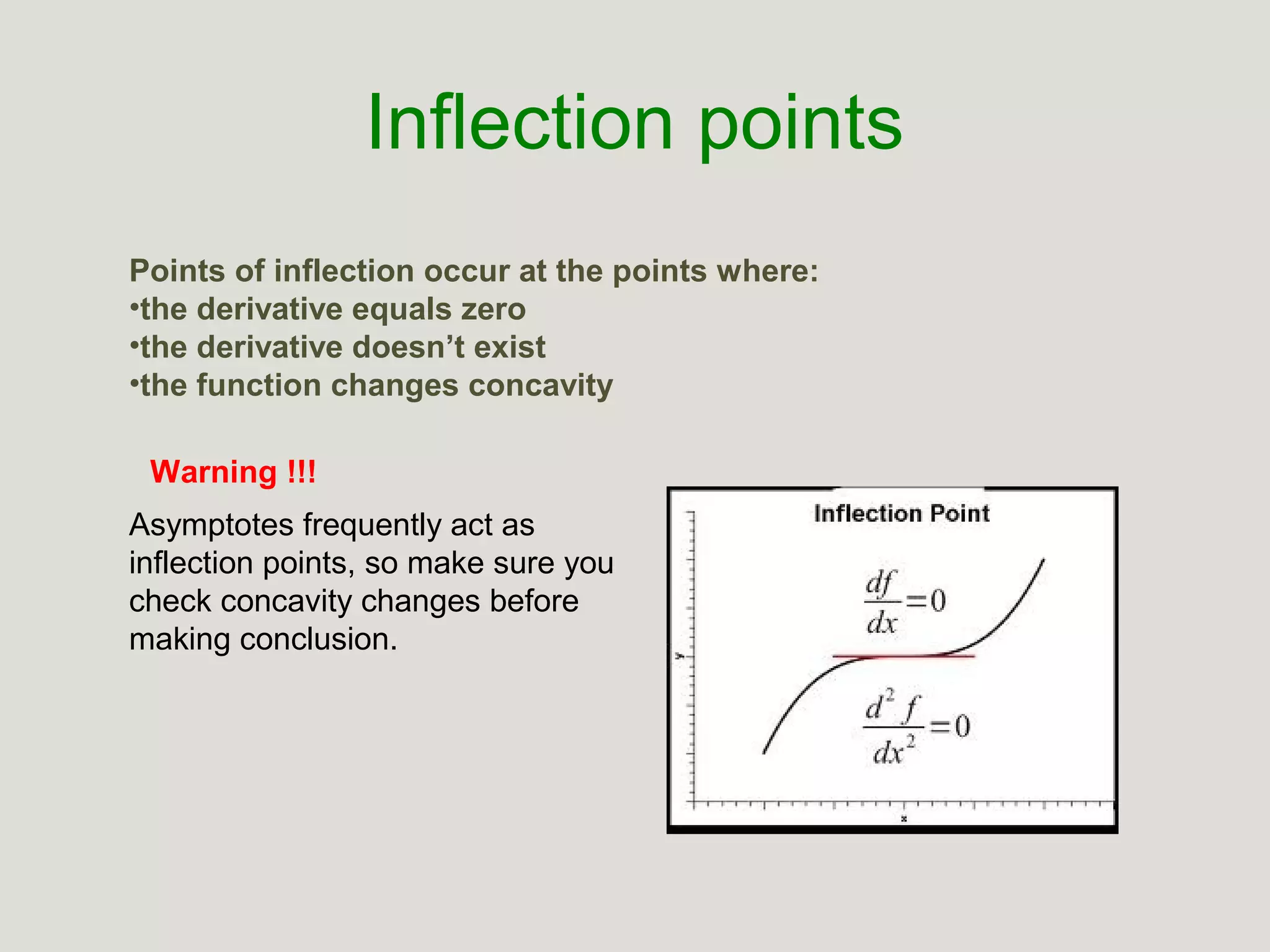
This document provides guidance on sketching the graph of functions by considering key features such as symmetries, intercepts, extrema, asymptotes, concavity, and inflection points. It then works through an example of sketching the graph of the function f(x) = (2x^2 - 8)/(x^2 - 16). Key aspects of this function identified are x-intercepts of -2 and 2, a vertical asymptote at x = -4 and 4, a horizontal asymptote at y = 2, and an inflection point at x = 4/3.

1. A Summary of Curve
Sketching

2. What should you consider?
•
•
•
•
•
•
•
•
•
symmetries
x-intercept
y-intercept
relative extrema
asymptores
concavity
inflection points
intervals of increase
interval of decrease
ASYMPTOTE – VA HA SA
N(x) ax m
Let R(x) =
=
D(x) bx n
VERTICAL ASYMPTOTE
If
D(x) = 0, then VA : x = c
HORIZONTAL ASYMPTOTE
If
m > n,
then HA : doesn't exist
If
m < n,
then HA : y = 0,
If
m = n,
then HA : y =
SLANT ASYMPTOTE
If
x - axis
a
b
m = n +1, then SA : y = mx + b
Long divide N(x) by D(x)

3. Let’s see how that
works!!!
2x 2 - 8
Sketch the graph of the equation f (x) = 2
x -16
2x - 8
=0
2
x -16
2
VA:
2x 2 - 8 = 0
x 2 -16 = 0
f '(x) =
f '(x) =
2 × 02 - 8 1
f (0) = 2
=
0 -16 2
x = -2, 2
x = -4, 4
HA:
4x ( x 2 -16) - 2x ( 2x 2 - 8)
(x
(x
2
-16)
16 ( x - 4)
2
-16) ( x 2 -16)
-
f '(x) =
2
=
16 ( x - 4)
·
-4
·
4
4x 3 - 64 - 4x 3 +16x
(x
2
-16)
f '(x) =
( x + 4) ( x - 4) ( x 2 -16)
-
y=2
m=n
+
2
=
16x - 64
(x
2
-16)
2
16
=0
2
( x + 4) ( x -16)

4. Almost Done !!!!
f "(x) =
-16 é( x 2 -16) + 2x ( x + 4)ù
ë
û
é( x + 4) ( x -16)ù
ë
û
2
2
-16 é x -16 + 2x + 8xù
ë
û
2
f "(x) =
f "(x) =
=0
2
é( x + 4) ( x 2 -16)ù
ë
û
2
-16 (3x - 4) ( x + 4)
( x + 4 ) ( x + 4) ( x
-
2
-16)
·
-4
2
=0
=0
f "(x) =
-16 é3x 2 + 8x -16ù
ë
û
é( x + 4) ( x -16)ù
ë
û
f "(x) =
2
2
-16 (3x - 4)
( x + 4) ( x
- · + · 4/3
4
=0
2
-16)
2
=0

5. Let’ make a list
•
•
•
•
•
•
•
•
•
-2, 2
x-intercept
0.5
y-intercept
-4, 4
VA
2
HA
________
SA
[ 4, +¥)
f(x)
( -¥, 4]
f(x)
______
X max
X min
4
• f(x) È
• f(x) Ç
• X infl
æ4 ö
ç , 4÷
è3 ø
æ
4ö
-¥, ÷ and ( 4, +¥)
ç
è
3ø
4
3

6. Sketch the graph of the equation
•
•
•
•
•
•
•
•
•
x-intercept
y-intercept
VA
HA
SA
f(x)
f(x)
X max
X min
• f(x)
• f(x)
• X infl
y = ( x - 4)
2
3

7. 1
3
Sketch the graph of the equation y = 6x + 3x
•
•
•
•
•
•
•
•
•
x-intercept
y-intercept
VA
HA
SA
f(x)
f(x)
X max
X min
• f(x)
• f(x)
• X infl
4
3