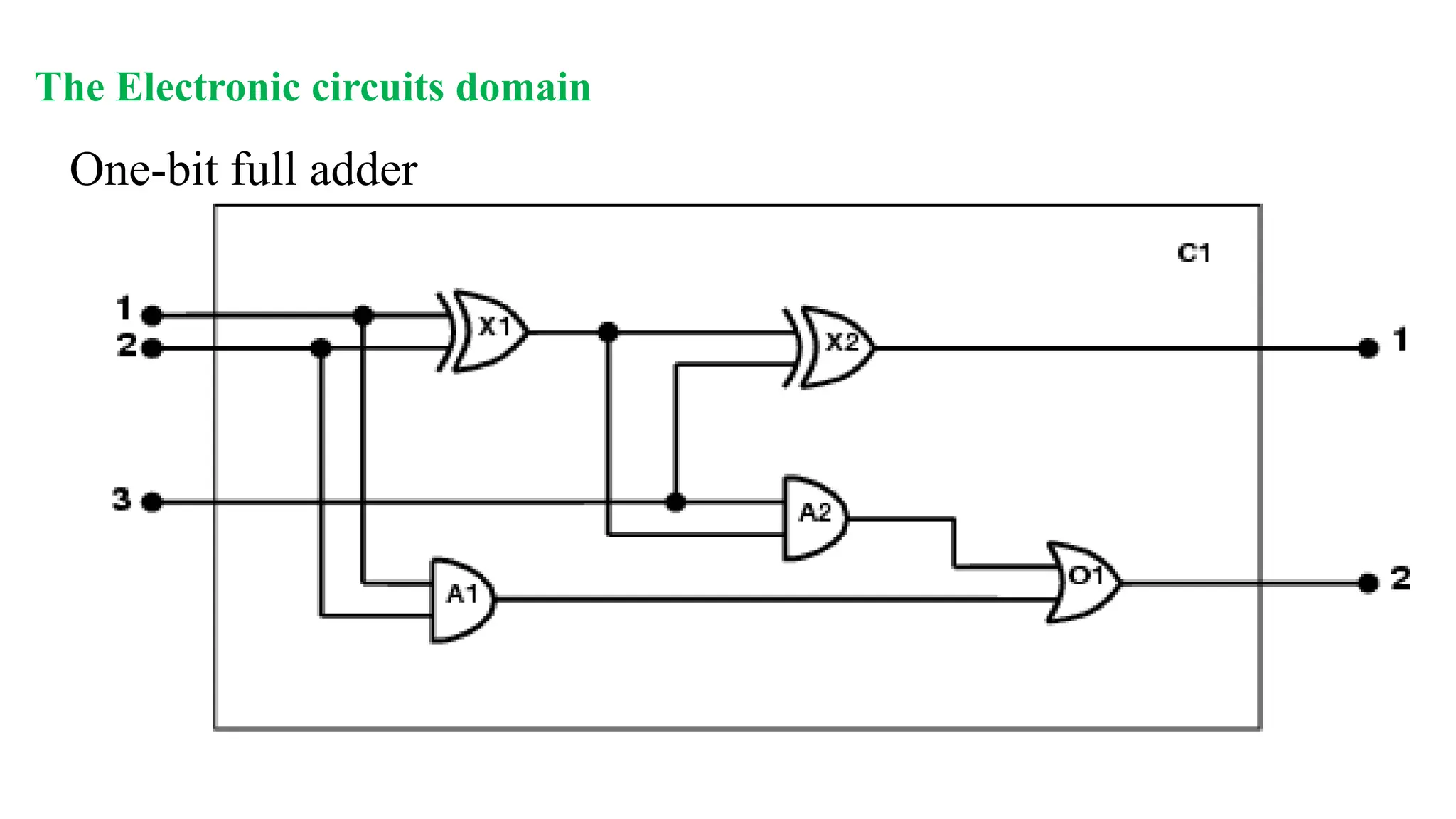
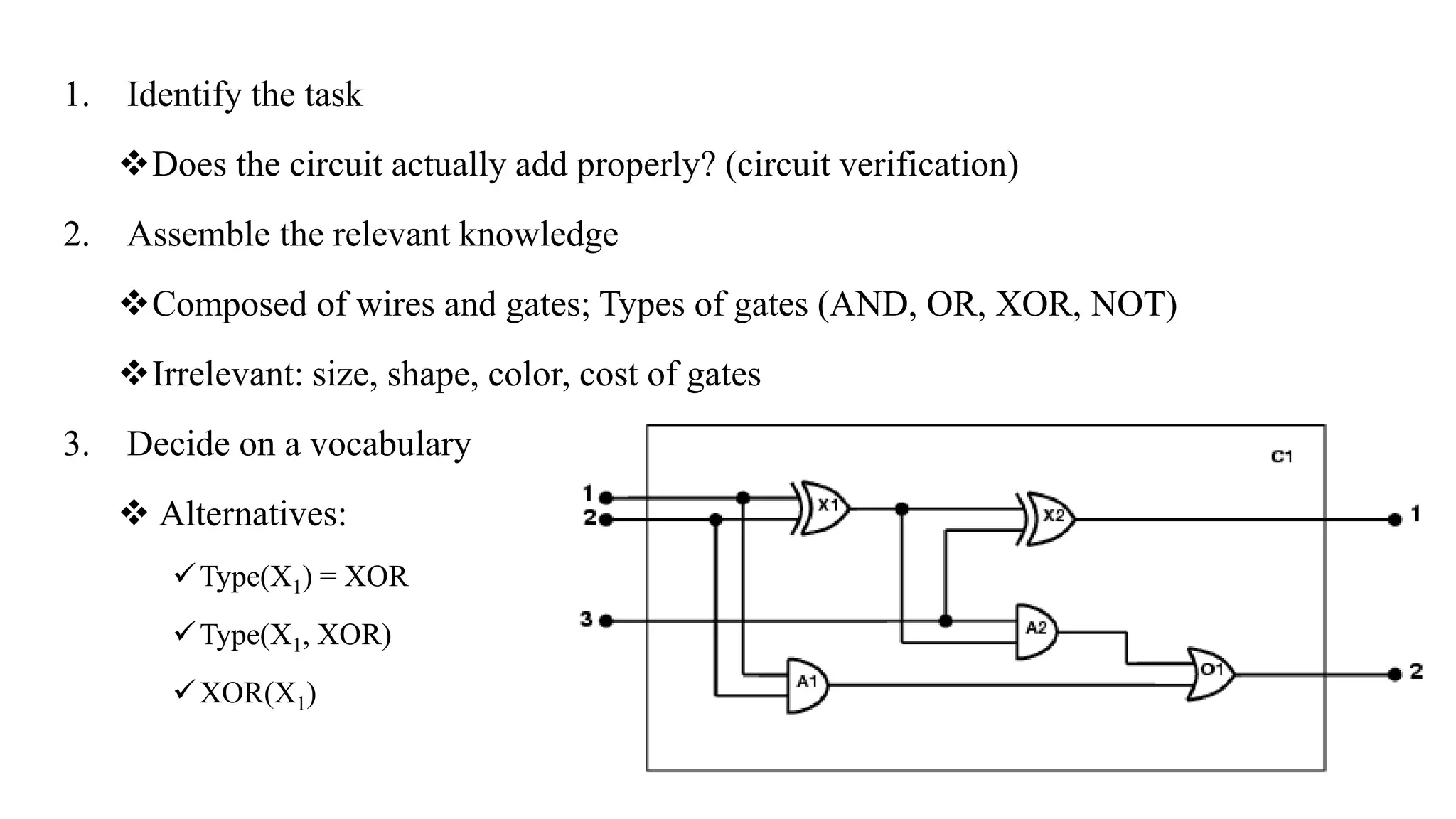
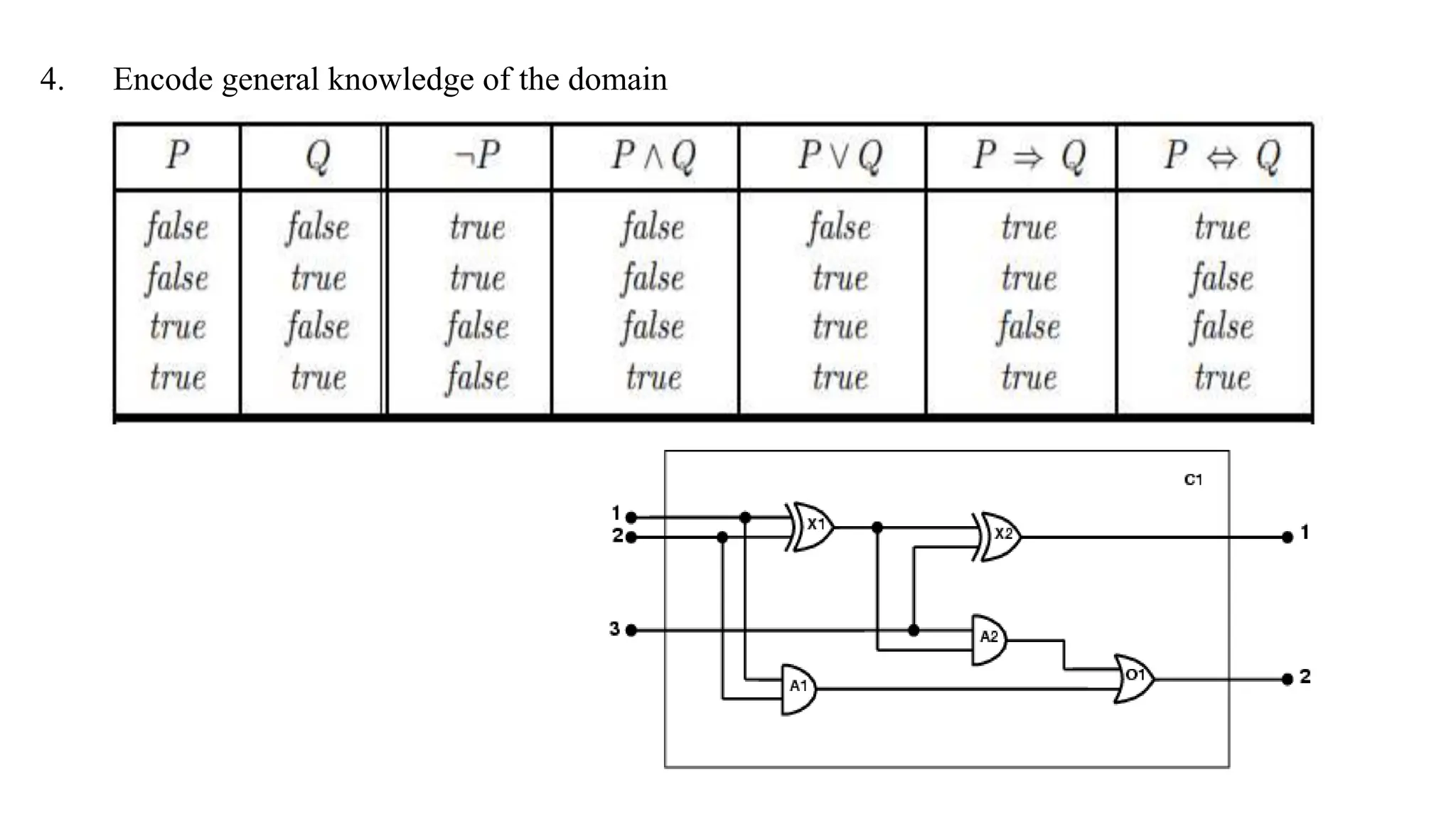
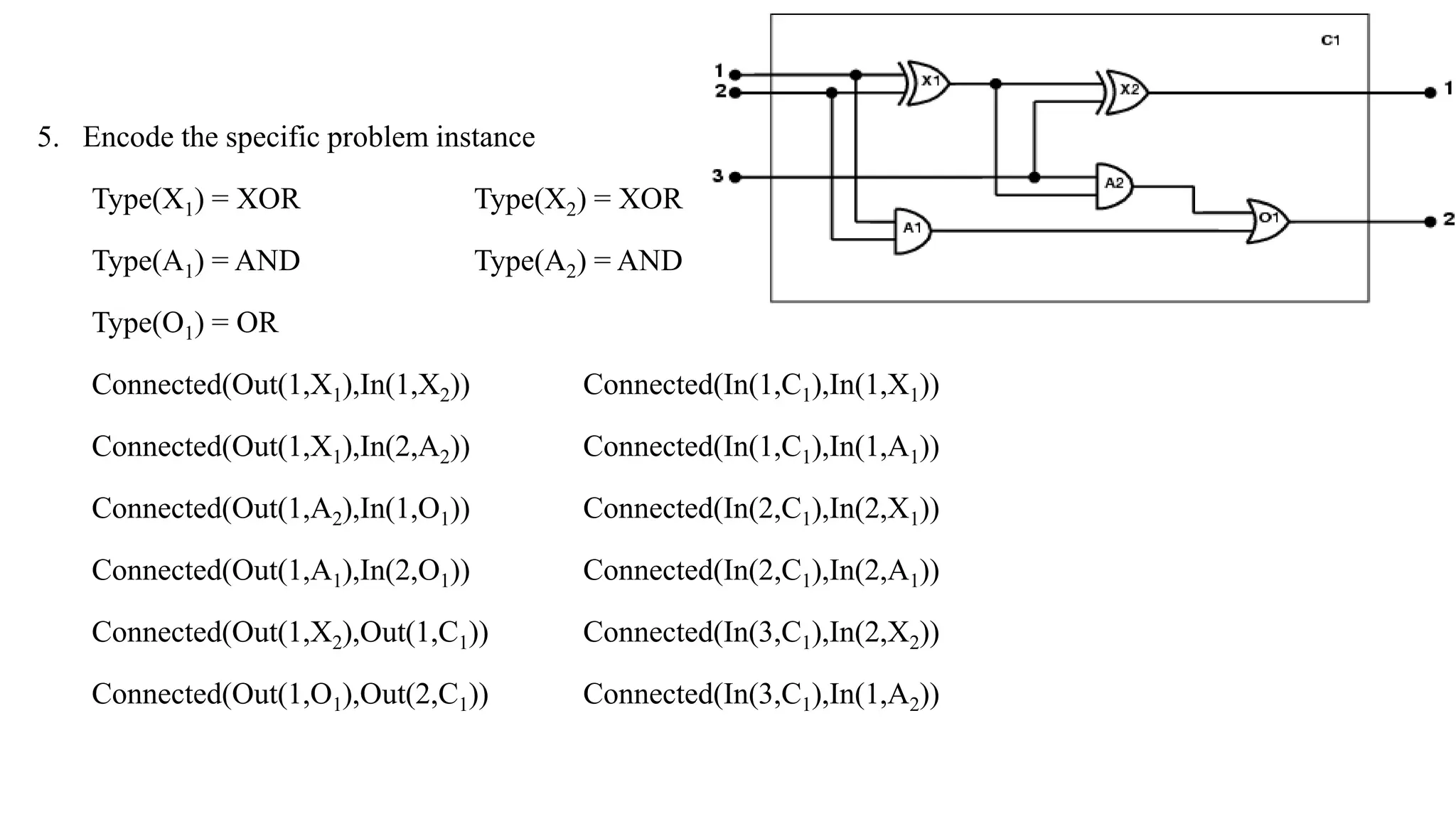
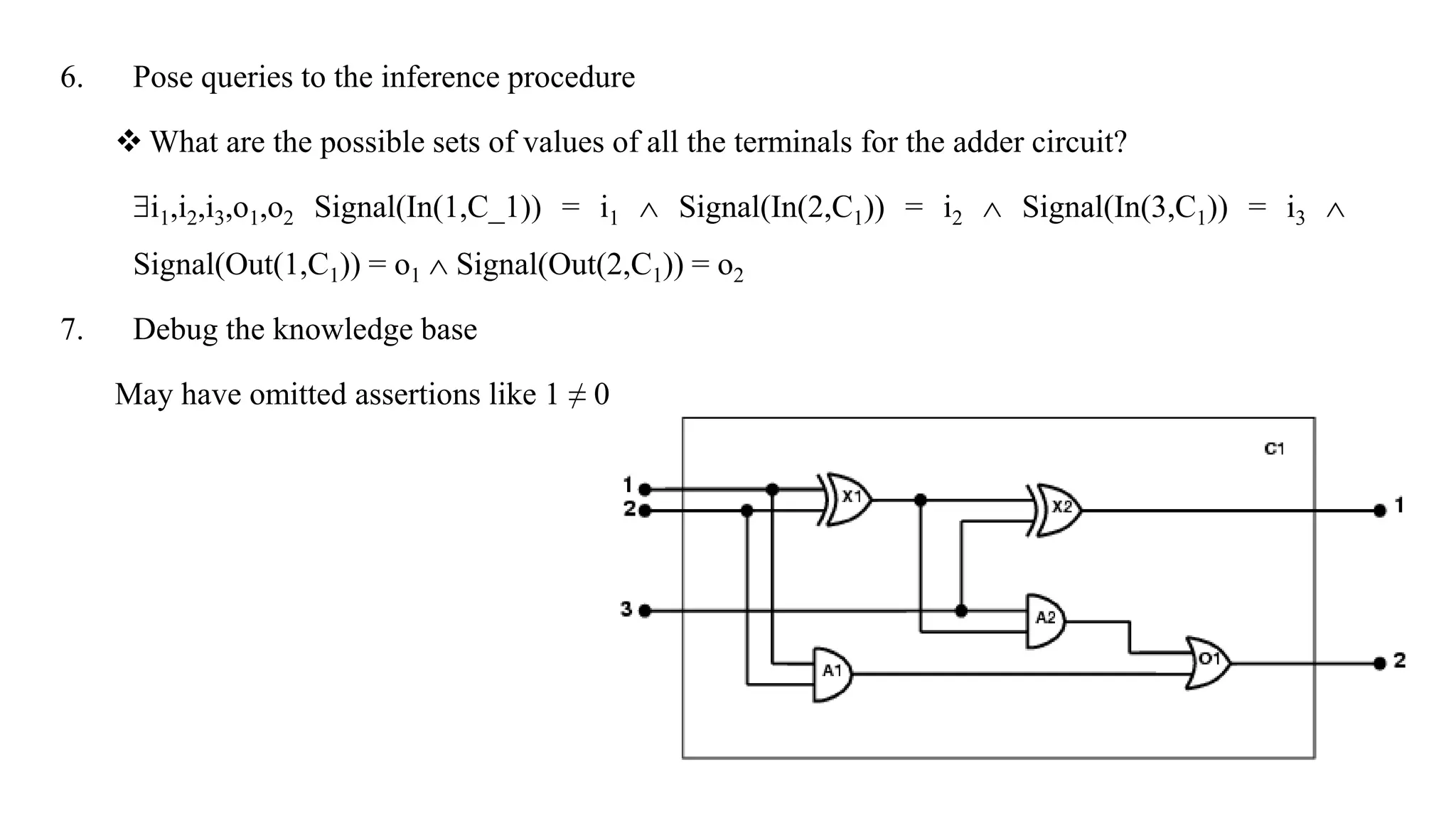
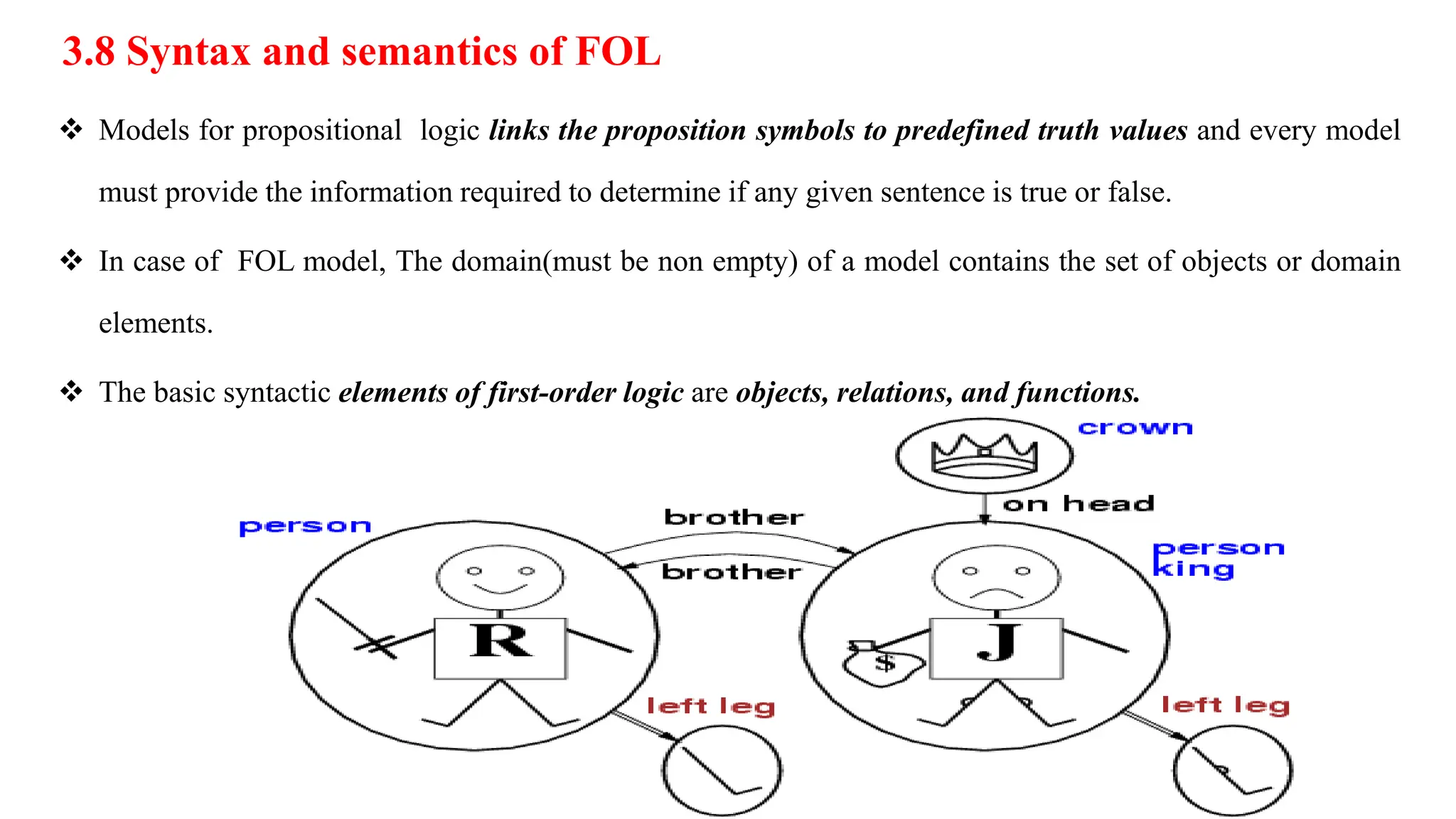
Chapter 8 discusses the comparison between propositional logic and first-order logic (FOL), highlighting FOL's capacity to represent objects, properties, relations, and functions more expressively. It explains the syntax and semantics of FOL, including terms, atomic sentences, quantifiers, and the construction of knowledge bases for logical assertions and queries. Additionally, practical applications of FOL in domains like kinship and electronic circuits are explored.

1. Chapter 8
First Order Logic(FOL)

2. 3.7 Representation Revisited
Pros and cons of propositional logic
 Propositional logic is declarative: the syntax correspond to facts.
 Propositional logic allows partial/disjunctive/negated information.
 Propositional logic is compositional: meaning of B1,1 ∧ P1,2 is derived from meaning of B1,1 and of
P1,2.
 Meaning in propositional logic is context-independent (unlike natural language, where meaning
depends on context).
X Propositional logic has very limited expressive power (unlike natural language).
 E.g., cannot say “pits cause breezes in adjacent squares” except by writing one sentence for each
square.

3. First-order logic
 Propositional logic assumes the world contains facts.
 First-order logic (FOL), models the world in terms of
 Objects, which are things with individual identities.
 Properties of objects that distinguish them from other objects
 Relations that hold among sets of objects
 Functions, which are a subset of relations where there is only one “value” for any given “input”,
 Examples:
 Objects: Students, lectures, companies, cars ...
 Relations: Brother-of, bigger-than, outside, part-of, has-color, occurs-after, owns, visits, precedes, ...
 Properties: blue, oval, even, large, ...
 Functions: father-of, best-friend, second-half, one-more-than ...

4. Propositional Logic vs FOL
 The primary difference between propositional and first-order logic lies in the ontological
commitment made by each language—that is, what it assumes about the nature of reality.
 A logic can also be characterized by its epistemological commitments—the possible states of
knowledge that it allows with respect to each fact.

5. 3.8 Syntax and semantics of FOL
 Models for propositional logic links the proposition symbols to predefined truth values and every model
must provide the information required to determine if any given sentence is true or false.
 In case of FOL model, The domain(must be non empty) of a model contains the set of objects or domain
elements.
 The basic syntactic elements of first-order logic are objects, relations, and functions.

6.  The symbols are categorized into three kinds:
1. constant symbols, which stand for objects;
2. predicate symbols, which stand for relations; and
3. function symbols, which stand for functions.
 In addition to objects, relations, and functions, each model includes an interpretation that specifies exactly which
objects, relations and functions are referred to by the constant, predicate, and function symbol.
 In summary, a model in first-order logic consists of
a set of objects and an interpretation that maps constant symbols to objects,
predicate symbols to relations on those objects, and
function symbols to functions on those objects.
 For example, we might use the constant symbols Richard and John; the predicate symbols Brother , OnHead, Person,
King, and Crown; and the function symbol LeftLeg.

7. Term, Atomic sentence ,Complex Sentence
 A term is a logical expression that refers to an object.
 For example, in English ,we can use the expression “King John’s left leg” rather than giving a
name to his leg.
 This is what function symbols are for: instead of using a constant symbol, we use
LeftLeg(John).
 An atomic sentence (or atom for short) is formed from a predicate symbol optionally followed
by a parenthesized list of terms, such as Brother(Richard, John).
 Complex sentences are formed by the atomic sentences which are connected by the logical
connectives.
 Example: Brother (Richard, John) ∧ Brother (John, Richard).

8. Quantifiers
 Quantifiers are used to express the quantity of something. First-order logic contains two standard quantifiers,
called universal quantifiers, and existential quantifiers.
 Universal quantifiers(∀):
 The universal quantifier express that , the statements within its scope are true for everything, or every
instance of a specific thing.
 “All kings are persons” is written in first-order logic as ∀ x King(x) ⇒ Person(x) .
 Existential quantification (∃):
 The existential quantifier is a symbol of symbolic logic which expresses that the statements within its scope
are true for at least one instance of something.
 King John has a crown on his head, we write ∃ x Crown(x) ∧ OnHead(x, John) .
 A quantified sentence adds quantifiers  and .

9.  A well-formed formula(wff) is a sentence containing no “free” variables. That is, all variables are “bound” by universal or
existential quantifiers. For example: (x)P(x,y) has x bound as a universally quantified variable, but y is free.
Properties of quantifiers
 x y is the same as y x
 x y is the same as y x
 x y is not the same as y x
 x y Loves(x,y)
“There is a person who loves everyone in the world”
 y x Loves(x,y)
“Everyone in the world is loved by at least one person.
Equality
 term1 = term2 is true under a given interpretation if and only if term1 and term2 refer to the same object.
 Equality symbol can be used to signify that , the two terms refer to the same object.
 For example: ∃ x, y Brother (x, Richard) ∧ Brother (y, Richard)

10. Syntax of first-order logic

11.  Operator precedence are specified, from highest to lowest.

12. 3.9 Using FOL
Assertions and queries in first-order logic
 Sentences are added to a knowledge base using TELL, such sentences are called assertions(confident
and forceful statement of fact or belief).
 For example, we can assert that John is a king, Richard is a person, and all kings are persons:
 TELL(KB, King(John)) .
 TELL(KB, Person(Richard)) .
 TELL(KB, ∀ x King(x) ⇒ Person(x)) .
 We can ask questions to the knowledge base using ASK.
 Questions asked with ASK are called queries or goals.
 For example, ASK(KB, King(John)) QUERY returns true.

13. The Kinship Domain
 For example if we consider the domain of family relationships, or kinship.
 This domain includes facts such as
“Elizabeth is the mother of Charles” and
“Charles is the father of William” and
 rules such as “One’s grandmother is the mother of one’s parent.”
 Clearly, the objects in kinship domain are people.
 Here there are two unary predicates, Male and Female.
 Kinship relations—parenthood, brotherhood, marriage, and so on—are represented by binary predicates: Parent,
Sibling, Brother , Sister , Child, Daughter, Son, Spouse, Wife, Husband, Grandparent, Grandchild , Cousin, Aunt, and
Uncle.
 Functions can be used for Mother and Father , because every person has exactly one of each of these.

14. For example,
 one’s mother is one’s female parent:
∀ m, c Mother (c) = m ⇔ Female(m) ∧ Parent(m, c) .
 One’s husband is one’s male spouse:
∀ w, h Husband(h, w) ⇔ Male(h) ∧ Spouse(h, w) .
 Male and female are disjoint categories:
∀ x Male(x) ⇔ ¬Female(x) .
 Parent and child are inverse relations:
∀ p, c Parent(p, c) ⇔ Child(c, p) .
 A grandparent is a parent of one’s parent:
∀ g, c Grandparent(g, c) ⇔ ∃ p Parent(g, p) ∧ Parent(p, c) .
 A sibling is another child of one’s parents:
∀ x, y Sibling(x, y) ⇔ x = y ∧ ∃ p Parent(p, x) ∧ Parent(p, y) .

15. Sets
 Set can be defined as the collection of well-defined objects.
 We can represent individual sets, including the empty set ,which can be represented by { }.
 Sets can be build , by adding an element to a set or taking the union or intersection of two sets.
 There is one unary predicate, Set, which is true of sets.
 The binary predicates are
x∈ s (x is a member of set s) and
s1 ⊆ s2 (set s1 is a subset of set s2).
 The binary functions are
s1 ∩ s2 (the intersection of two sets),
s1 ∪ s2 (the union of two sets), and
{x|s} (the set resulting from adjoining element x to set s).

16. Set of Axioms
 The only sets are the empty set and those made by adjoining something to a set:
∀ s Set(s) ⇔ (s = { }) ∨ (∃ x, s2 Set(s2) ∧ s = {x|s2}) .
 The empty set has no elements adjoined into it(it can not be decomposed):
¬∃ x, s {x|s} = { } .
 Adjoining an element already in the set has no effect:
∀ x, s x∈ s ⇔ s = {x|s} .
 The only members of a set are the elements that were adjoined into it.(saying that x is a
member of s if and only if s is equal to some set s2 adjoined with some element y, where
either y is the same as x or x is a member of s2):
∀ x, s x∈ s ⇔ ∃ y, s2 (s = {y|s2} ∧ (x = y ∨ x∈ s2)) .

17.  A set is a subset of another set if and only if all of the first set’s members are members of
the second set:
∀ s1, s2 s1 ⊆ s2 ⇔ (∀ x x∈ s1 ⇒ x∈ s2) .
 Two sets are equal if and only if each is a subset of the other:
∀ s1, s2 (s1 = s2) ⇔ (s1 ⊆ s2 ∧ s2 ⊆ s1)
 An object is in the intersection of two sets if and only if it is a member of both sets:
∀ x, s1, s2 x∈ (s1 ∩ s2) ⇔ (x∈ s1 ∧ x∈s2) .
 An object is in the union of two sets if and only if it is a member of either set:
∀ x, s1, s2 x∈ (s1 ∪ s2) ⇔ (x∈ s1 ∨ x∈s2)

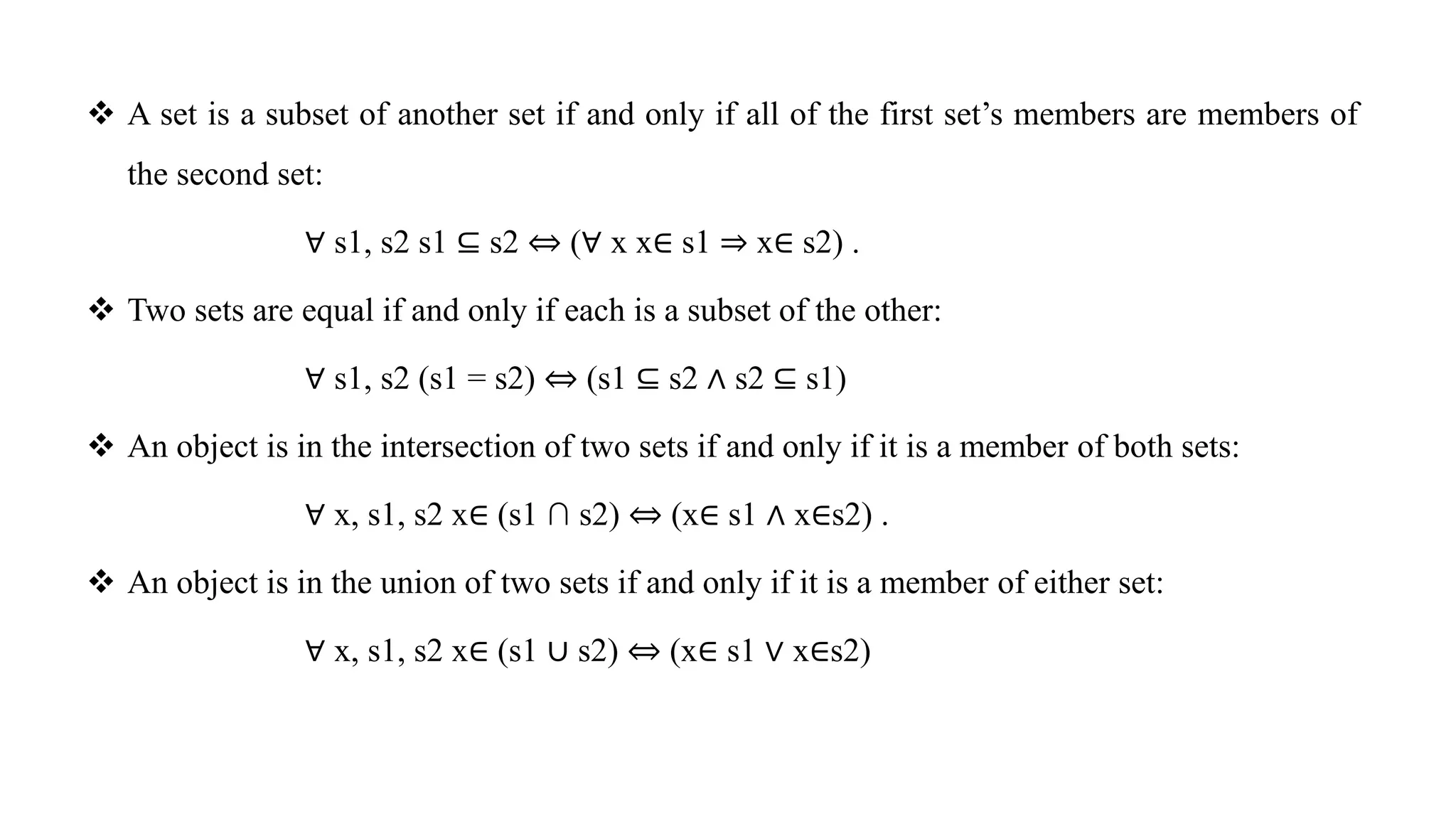
18. The wumpus world
 The agent percepts can be represented as five element list, [Stench, Breeze, Glitter, Bump, Scream].
 The corresponding first-order sentence stored in the knowledge base must include both the percept and the time
at which it occurred; otherwise, the agent will get confused about when it perceived what(integers time
stamps).
 For example the agent perceived ([Stench, Breeze, Glitter , None, None], 5) .
 Here, Percept is a binary predicate, and Stench and so on are constants placed in a list.
 The actions in the wumpus world can be : Turn(Right), Turn(Left), Forward, Shoot, Grab.
 To determine which is best, the agent program executes the query
ASKVARS(∃ a BestAction(a, 5)) ,
which returns a binding list such as {a/Grab}.
 The agent program can then return Grab as the action to take.

19. 3.10 Knowledge Engineering in FOL
 Knowledge engineering can be defined as the Construction of knowledge-base.
 Steps to construct the knowledge base
1. Identify the task
2. Assemble the relevant knowledge (knowledge acquisition: extract what they(expert) know)
3. Decide on a vocabulary of predicates, functions, and constants
4. Encode general knowledge about the domain
5. Encode a description of the specific problem instance
6. Pose queries to the inference procedure and get answers
7. Debug the knowledge base

20. The Electronic circuits domain
One-bit full adder

21. 1. Identify the task
Does the circuit actually add properly? (circuit verification)
2. Assemble the relevant knowledge
Composed of wires and gates; Types of gates (AND, OR, XOR, NOT)
Irrelevant: size, shape, color, cost of gates
3. Decide on a vocabulary
 Alternatives:
Type(X1) = XOR
Type(X1, XOR)
XOR(X1)

22. 4. Encode general knowledge of the domain

23. 5. Encode the specific problem instance
Type(X1) = XOR Type(X2) = XOR
Type(A1) = AND Type(A2) = AND
Type(O1) = OR
Connected(Out(1,X1),In(1,X2)) Connected(In(1,C1),In(1,X1))
Connected(Out(1,X1),In(2,A2)) Connected(In(1,C1),In(1,A1))
Connected(Out(1,A2),In(1,O1)) Connected(In(2,C1),In(2,X1))
Connected(Out(1,A1),In(2,O1)) Connected(In(2,C1),In(2,A1))
Connected(Out(1,X2),Out(1,C1)) Connected(In(3,C1),In(2,X2))
Connected(Out(1,O1),Out(2,C1)) Connected(In(3,C1),In(1,A2))

24. 6. Pose queries to the inference procedure
 What are the possible sets of values of all the terminals for the adder circuit?
i1,i2,i3,o1,o2 Signal(In(1,C_1)) = i1  Signal(In(2,C1)) = i2  Signal(In(3,C1)) = i3 
Signal(Out(1,C1)) = o1  Signal(Out(2,C1)) = o2
7. Debug the knowledge base
May have omitted assertions like 1 ≠ 0