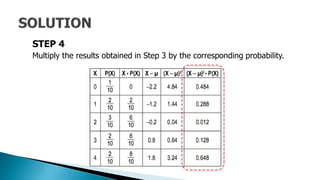
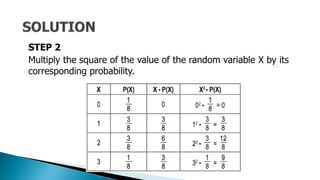
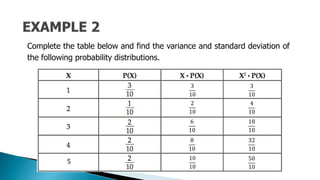
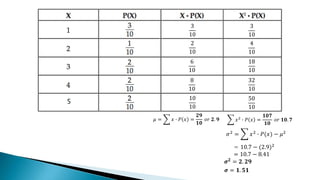
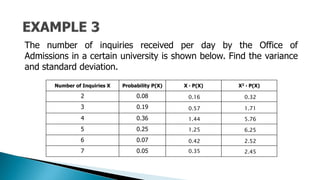
The document provides a detailed lesson on calculating the variance and standard deviation of discrete probability distributions for Grade 11 statistics. It outlines steps to compute these measures using provided examples, including car sales and coin tosses, along with the relevant formulas. The document also emphasizes the interpretation of variance and standard deviation in terms of spread and variability.

1. DOMINIC DALTON L. CALING
Statistics and Probability | Grade 11

2. At the end of this lesson, you are expected to:
 illustrate and calculate the variance of a discrete random variable;
 interpret the variance of a discrete random variable; and
 solve problems involving variance of probability distributions.

3. The variance and standard deviation describe the amount of
spread, dispersion, or variability of the items in a distribution.
How do you describe the spread or dispersion in a probability
distribution?

4. Steps in Finding the Variance and Standard Deviation of
a Discrete Probability Distribution
1. Find the mean of the probability distribution.
2. Subtract the mean from each value of the random variable X.
3. Square the results obtained in Step 2.
4. Multiply the results obtained in Step 3 by the corresponding
probability.
5. Get the sum of the results obtained in Step 4.

5. The number of cars sold per day at a local car dealership,
along with its corresponding probabilities, is shown in the
succeeding table. Compute the variance and the standard
deviation of the probability distribution.

6. STEP 1
Find the mean of the
probability distribution
using the formula
𝜇 = 𝑥 ∙ 𝑃(𝑥)

7. STEP 2
Subtract the mean from each value of the random variable X.

8. STEP 3
Square the results obtained in Step 2.

9. STEP 4
Multiply the results obtained in Step 3 by the corresponding probability.

10. STEP 5
Get the sum of the results
obtained in Step 4. The result
is the value of the variance.
So, the formula for the
variance is:
𝜎2 = 𝑥 − 𝜇 2 ∙ 𝑃(𝑥)

11. Step 6
Get the square root of the variance to get the standard
deviation.
The variance of the probability distribution is σ2 = 1.56.
The standard deviation is σ = 1.56 = 1.25

13. 1. Find the mean of the probability distribution.
2. Multiply the square of the value of the random variable X by
its corresponding probability.
3. Get the sum of the results obtained in Step 2.
4. Subtract the mean from the results obtained in Step 3.

14. Number of Heads
When three coins are tossed, the probability distribution
for the random variable X representing the number of
heads that occur is given below. Compute the variance
and standard deviation of the probability distribution.

15. STEP 1
Find the mean of the probability distribution using the formula:
𝜇 = 𝑥 ∙ 𝑃(𝑥)

16. STEP 2
Multiply the square of the value of the random variable X by its
corresponding probability.

17. STEP 3
Get the sum of the results obtained in Step 2.

18. STEP 4
Subtract the square of the mean from the results obtained in
Step 3 to get the variance. So, the formula for the variance of
a probability distribution is given by 𝜎2 = 𝑥2 ∙ 𝑃(𝑥) − 𝜇2.
The standard deviation is the square root of the variance.
Thus, 𝜎 = 𝑥2 ∙ 𝑃 𝑥 − 𝜇2.

19. STEP 4
The variance is given by
𝜎2 = 𝑥 − 𝜇 2 ∙ 𝑃(𝑥) -𝜇2
𝜎2
= 3 − 1.5 2
𝝈𝟐
= 𝟎. 𝟕𝟓
The standard deviation is
𝜎 = 0.75
𝝈 = 𝟎. 𝟖𝟕

20. Complete the table below and find the variance and standard deviation of
the following probability distributions.
3
10
2
10
6
10
8
10
10
10
3
10
4
10
18
10
32
10
50
10
5

21. 3
10
2
10
6
10
8
10
10
10
3
10
4
10
18
10
32
10
50
10
5
𝜇 = 𝑥 ∙ 𝑃 𝑥 =
𝟐𝟗
𝟏𝟎
𝑜𝑟 𝟐. 𝟗 𝑥2
∙ 𝑃 𝑥 =
𝟏𝟎𝟕
𝟏𝟎
𝑜𝑟 𝟏𝟎. 𝟕
𝜎2 = 𝑥2 ∙ 𝑃(𝑥) − 𝜇2
= 10.7 − (2.9)2
= 10.7 − 8.41
𝝈𝟐
= 𝟐. 𝟐𝟗
𝝈 = 𝟏. 𝟓𝟏

22. The number of inquiries received per day by the Office of
Admissions in a certain university is shown below. Find the variance
and standard deviation.
Number of Inquiries X Probability P(X) X ∙ P(X) X2 ∙ P(X)
2 0.08
3 0.19
4 0.36
5 0.25
6 0.07
7 0.05
0.16
0.57
1.44
1.25
0.42
0.35
0.32
2.52
6.25
5.76
1.71
2.45

23. To find the variance of the probability distribution,
1. Find the mean of the probability distribution.
2. Multiply the square of the value of the random variable X by
its corresponding probability.
3. Get the sum of the results obtained in Step 2.
4. Subtract the mean from the results obtained in Step 3.