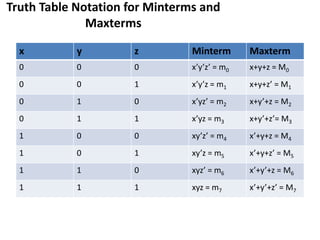
The document discusses Boolean functions and their representation in normal forms. It defines key concepts such as literals, product terms, sum terms, sum of products (SOP) form, product of sums (POS) form, standard form, non-standard form, minterms, maxterms, canonical form, conversion between forms, and shorthand notation using Σ and Π. Examples are provided to illustrate Boolean expressions in SOP and POS forms, their expansion to minterms and maxterms, and conversion between standard and canonical forms.

1. Boolean Functions and their
Representation

2. Normal Form
• A Boolean variable in true form or in complemented form is called
a literal. Thus a,b,c, (a’,b’,c’) and so on are literals.
• The Boolean product of two or more literals is called a product
term.
• The Boolean sum of two or more literals is called a sum term.
• When a Boolean function appears as a sum of several product
terms, it is said to be expressed as a sum of products (SOP). The
SOP form is also called the disjunctive normal form (DNF).
• When a Boolean function appears as a product of several sum
terms, it is said to be expressed as a product of sums (POS). The
POS form is also called the conjunctive normal form (CNF).

3. Examples
Example 1
f(a,b,c,d)=a’+b.c’+c.d
is an expression in SOP form or DNF.
Example 2
f(a,b,c,d)=(a+b).(b+c+d)
is an expression in POS form or CNF.

4. Standard and Non-Standard Form
• The standard form of the Boolean function is when it is expressed
in sum of the products or product of the sums fashion.
For example: Y =AB + BC + AC or Y = (A + B + C)(A + B′ + C)(A + B +
C′) are the standard forms.
• However, Boolean functions are also sometimes expressed in
nonstandard forms like F = (AB + CD)(A′B′ + C′D′), which is neither
a sum of products form nor a product of sums form. However, the
same expression can be converted to a standard form with help of
various Boolean properties, as: F = (AB + CD)(A′B′ + C′D′) = A′B′CD
+ ABC′D′

5. Minterm and Maxterm
• Minterm: a product term in which all the variables
appear exactly once, either complemented or
uncomplemented.
• Maxterm: a sum term in which all the variables
appear exactly once, either complemented or
uncomplemented

6. Minterm
• Represents exactly one combination in the truth table.
• Denoted by mj, where j is the decimal equivalent of the
minterm’s corresponding binary combination (bj).
• A variable in mj is complemented if its value in bj is 0,
otherwise is uncomplemented.
• Example: Assume 3 variables (A,B,C), and j=3.
Then, bj = 011 and its corresponding minterm is
denoted by mj = A’BC

7. Maxterm
• Denoted Represents exactly one combination in the
truth table.
• by Mj, where j is the decimal equivalent of the
maxterm’s corresponding binary combination (bj).
• A variable in Mj is complemented if its value in bj is 1,
otherwise is uncomplemented.
• Example: Assume 3 variables (A,B,C), and j=3. Then, bj =
011 and its corresponding maxterm is denoted by Mj =
A+B’+C’

8. Truth Table Notation for Minterms and
Maxterms
x y z Minterm Maxterm
0 0 0 x’y’z’ = m0 x+y+z = M0
0 0 1 x’y’z = m1 x+y+z’ = M1
0 1 0 x’yz’ = m2 x+y’+z = M2
0 1 1 x’yz = m3 x+y’+z’= M3
1 0 0 xy’z’ = m4 x’+y+z = M4
1 0 1 xy’z = m5 x’+y+z’ = M5
1 1 0 xyz’ = m6 x’+y’+z = M6
1 1 1 xyz = m7 x’+y’+z’ = M7

9. Canonical Form
• When each of the terms of a Boolean functions is
expressed either in SOP or POS form has all the
variables in it it is said to be expressed in canonical
form.
• The canonical SOP form is called the disjunctive
canonical form (DCF) and the canonical POS form is
called the conjunctive canonical form (CCF).

10. Conversion of SOP from Standard to
Canonical Form
• Expand non-canonical terms by inserting
equivalent of 1 in each missing variable x:
(x + x’) = 1
• Remove duplicate minterms
• f1(a,b,c) = a’b’c + bc’ + ac’
= a’b’c + (a+a’)bc’ + a(b+b’)c’
= a’b’c + abc’ + a’bc’ + abc’ + ab’c’
= a’b’c + abc’ + a’bc + ab’c’

11. Conversion of POS from Standard to
Canonical Form
• Expand noncanonical terms by adding 0 in terms of
missing variables (e.g., xx’ = 0) and using the
distributive law.
• Remove duplicate maxterms
• f1(a,b,c) = (a+b+c)•(b’+c’)•(a’+c’)
= (a+b+c)•(aa’+b’+c’)•(a’+bb’+c’)
= (a+b+c)•(a+b’+c’)•(a’+b’+c’)•
(a’+b+c’)•(a’+b’+c’)
= (a+b+c)•(a+b’+c’)•(a’+b’+c’)•(a’+b+c’)

12. Examples
Express the following functions in canonical forms
a) f1=a.b’.c+b.c’+a.c
b) f2=(a+b).(b+c’)
Solutions:
a) f1 =a.b’.c+b.c’+a.c
=a.b’.c+(a+a’).b.c’+a.(b+b’).c
=a.b’.c+a. b.c’ +a’.b.c’+a.b.c+a.b’.c
b) f2 = (a+b)(b+c’)
= (a+b+c.c’)(a.a’+b+c’)
= (a+b+c).(a+b+c’).(a+b+c’).(a’+b+c’)
= (a+b+c).(a+b+c’).(a’+b+c’)
f1 is expressed in DCF,
f2 is expressed in CCF.

13. Shorthand: ∑ and ∏
• f1(a,b,c) = ∑ m(1,2,4,6), where ∑ indicates that this is
a sum-of-products form, and m(1,2,4,6) indicates
that the minterms to be included are m1, m2, m4, and
m6.
• f1(a,b,c) = ∏ M(0,3,5,7), where ∏ indicates that this
is a product-of-sums form, and M(0,3,5,7) indicates
that the maxterms to be included are M0, M3, M5,
and M7.
• Since mj = Mj’ for any j,
f1(a,b,c) = ∑ m(1,2,4,6) = ∏ M(0,3,5,7)

14. Expansion of Boolean Expression to SOP
Form
Expand A’ + B’ to minterms and maxterms:
A’+B’= A’(B+B’) + B’ (A+A’)
= A’B+A’B’ + AB’+A’B’
= A’B+A’B’+AB’
= 01 + 00 + 10
= ∑ m(0,1,2)
∏ M(3)

15. Contd.
Expand A+BC’+ABD’ to minterms and maxterms:
A+BC’+ABD’ = A(B+B’) (C+C’) (D+D’) + BC’(A+A’) (D+D’) +
ABD’ (C+C’)
=ABCD+ABCD’+ABC’D+ABC’D’+AB’CD+AB’CD’+AB’C’D+
AB’C’D’ + ABC’D+ABC’D’+A’BC’D+AB’CD’ + ABCD’+ABC’D’
= ∑ m(4,5,8,9,10,11,12,13,14,15)
∏ M(0,1,2,3,6,7)

16. Expansion of Boolean Expression to
POS Form
Expand A(B’+A)B to maxterms and minterms:
A(B’+A)B = (A+B)(A+B’) (A+B’) (A+B) (A’+B)
= (A+B) (A+B’) (A’+B)
= (00) (01) (10)
= ∏ M(0,1,2)
∑ m(3)

17. Activity 1
1. The terms in SOP are called ___________
a) max terms
b) min terms
c) mid terms
d) sum terms
1. Which of the following is an incorrect SOP expression?
a) x+x.y
b) (x+y)(x+z)
c) x
d) x+y

18. Contd.
3. The corresponding min term when x=0, y=0 and z=1.
a) x.y.z’
b) X’+Y’+Z
c) X+Y+Z’
d) x’.y’.z
4. Convert to canonical SOP function F = x y + x z + y z
5. Convert to canonical POS form
F = (A’ + B + C) * (B’ + C + D’) * (A + B’ + C’ + D)

19. Contd.
7. Expand A’+B+CA to minterms and maxterms
8. Expand A(A’+B) (A’+B+C’) to maxterms and minterms

20. Thank You!!