This document provides information on combinational logic circuits and techniques for analyzing them, including:
1. Combinational circuits have outputs that solely depend on current inputs, unlike sequential circuits which use memory elements.
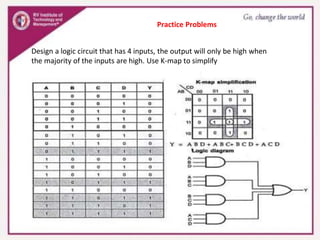
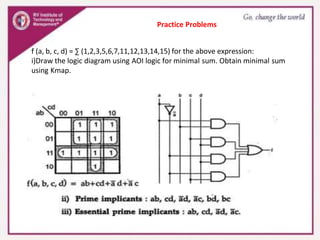
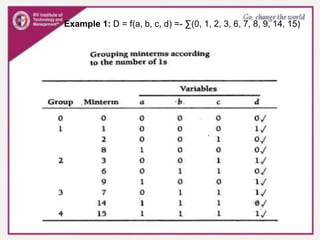
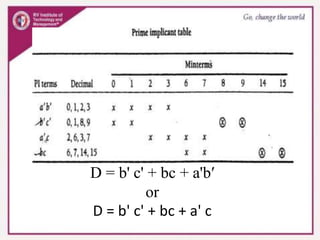
2. Truth tables are used to represent the relationships between inputs and outputs, and techniques like Karnaugh maps can simplify Boolean expressions.
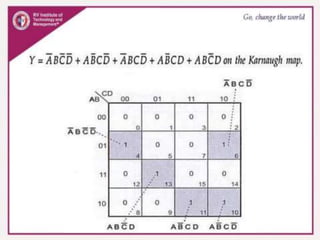
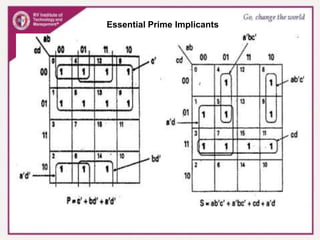
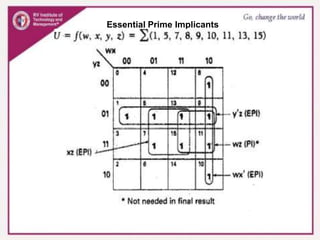
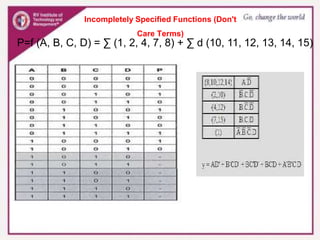
3. Karnaugh maps arrange minterms or maxterms in a grid, allowing groups of redundant variables to be identified and simplified. Standard forms like sum of products can be plotted and minimized on the map.