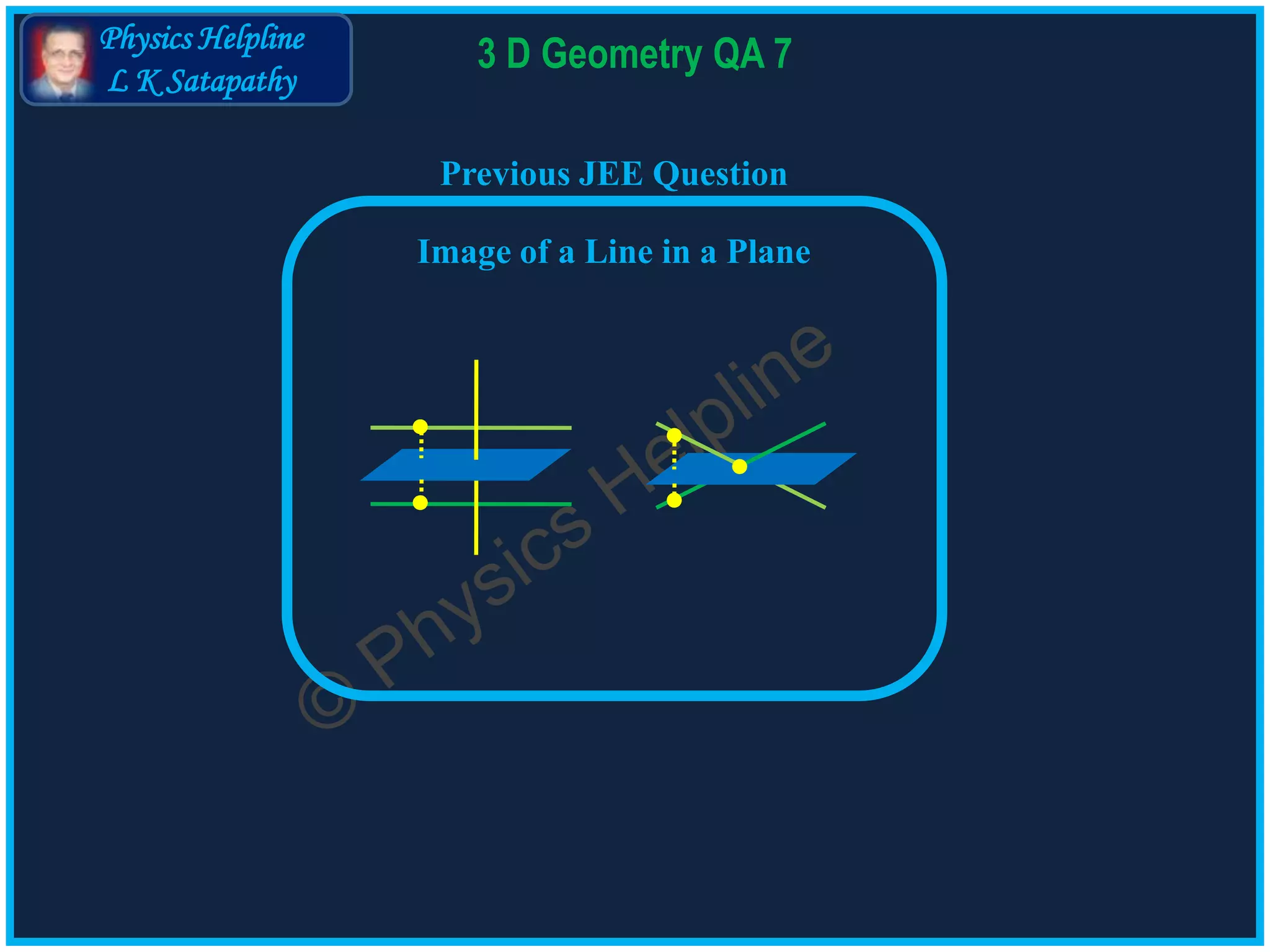
The document discusses the derivation of the image line in 3D geometry intersecting a given plane defined by the equation 2x – y + z + 3 = 0. It includes calculations of direction ratios for both the line and the plane, discusses cases of parallelism and intersection, and outlines the steps for finding the image of a point with respect to the plane. Additionally, it provides a specific example with the coordinates and formula for the image line.

1. Physics Helpline
L K Satapathy
3D Geometry QA 7

2. Physics Helpline
L K Satapathy
3 D Geometry QA 7
Question: The image of the line
Answer :
31 4
3 1 5
yx z  

in the plane 2x – y + z + 3 = 0 , is the line
53 2( )
3 1 5
yx za
  

53 2( )
3 1 5
yx zb
  
 
53 2( )
3 1 5
yx zc
  

53 2( )
3 1 5
yx zd
  
 
Equation of the given line is 31 4 . . . (1)
3 1 5
yx z  

 The DRs of the line = ( 3 , 1 , – 5 ) and ( 1 , 3 , 4 ) is a point on the line
Equation of the given plane is 2x – y + z + 3 = 0 . . . (2)
 The DRs of normal to the plane = ( 2 , – 1 , 1 )

3. Physics Helpline
L K Satapathy
3 D Geometry QA 7
Case-1:
 The image line is parallel to the given line
 The direction ratios of the image line = those of the given line
 Knowing DRs and a point , we write the equation of the image line
Case-2:
The point of intersection is also a point on the image line
 Knowing two points on the image line , we can write its equation
If the line is parallel to the plane , the image line is also parallel to the plane
If the line is intersecting the plane , we find the point of intersection
Step-1: Find the image of the point ( 1 , 3 , 4 ) in the plane
Step-2: Find if the line is parallel to the plane or intersecting it

4. Physics Helpline
L K Satapathy
3 D Geometry QA 7
Now , (2)(3) + (–1)(1) + (1)(–5) = 6 – 1 – 5 = 0
 Direction ratios of image line = ( 3 , 1 , –5 )
Equation of line through ( 1 , 3 , 4 ) and perpendicular to plane (2) is
31 4 . . . (3)
2 1 1
yx z 
   

 Coordinates of any point on line (3) (2 1, 3 , 4)      
 Line is perpendicular to the normal of plane
DRs of the line = ( 3 , 1 , – 5 ) and DRs of normal to the plane = ( 2 , – 1 , 1 )
 Line is parallel to the plane
To find the image of the point (1 , 3 , 4) :

5. Physics Helpline
L K Satapathy
3 D Geometry QA 7
If the point lies on plane(2 1, 3 , 4)      2 3 0x y z   
2(2 1) ( 3) ( 4) 3 0 6 6 0 1                 
 Foot of the perpendicular on plane
Let image of (1 , 3 , 4) = 1 1 1( , , )x y z
1 1 11 3 4
, , ( 1 , 4 , 3)
2 2 2
x y z   
   
 
53 2
3 1 5
yx z  

 Equation of image line having direction ratios (3 , 1 , – 5 )
Correct option = (a)
(2 1, 3 , 4) ( 1, 4 , 3)        
1 1 1( , , ) ( 3, 5, 2)x y z  
and passing through the point ( – 3 , 5 , 2 ) is given by

6. Physics Helpline
L K Satapathy
For More details:
www.physics-helpline.com
Subscribe our channel:
youtube.com/physics-helpline
Follow us on Facebook and Twitter:
facebook.com/physics-helpline
twitter.com/physics-helpline