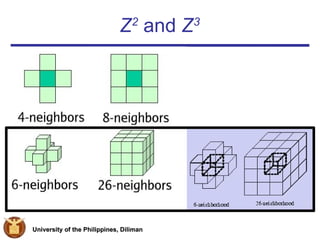
The document summarizes research on digital topologies and admissible labelings on integer grids. It discusses neighbors and connectivity in Zd, definitions of digital topologies, and prior work counting topologies in low dimensions. The authors develop an algorithm to find and count isomorphism classes of admissible labelings on Z2d to obtain bounds on digital topologies in higher dimensions. Initial results are presented for Z5 along with proposals for further work.

1. 28 October 2006 On Admissible Labelings and Digital Topologies Alva Benedict C. Balbuena & Evelyn L. Tan Research partially funded by the UP Natural Sciences Research Institute, Diliman, Quezon City

2. Digital Topology Study of topological properties of digital images Closely related with digital geometry Applications in computer vision, image analysis, computer graphics..

3. Z 2 and Z 3

4. Neighbors Let x = (n 1 ,n 2 ,...,n d ) and y = (m 1 ,m 2 ,...,m d )  Z d ie. ie. x, y (3 d -1)-neighbors if || x-y || ∞ x, y 2d-neighbors if || x-y || 1

5. 2d-Connected M ⊆ Z d 2d-connected if  x,y ∈ M, ∃ 2d-path from x to y in M * analogous for (3 d -1)-connected

6. Digital Topologies on Z d D1 D2 D3 Topologies on Z d satisfying

7. Counting Digital Topologies Khalimsky line: Marcus-Wyse Alexandroff-Hopf In Z 2 , only 2 digital topologies (Eckhardt, Latecki 2002) In Z, only 1 digital topology

8. Counting Digital Topologies In Z 3 , only 5 digital topologies (Eckhardt, Latecki 2002) In Z 4 , only 24 digital topologies (Kong 2004) In Z 5 ???

9. Open Problem

10. Stable Sets of Z 2 d M ⊆ Z 2 d where none of its elements are 2d-neighbors Also called stable subsets of the hypercube Q d (vertices are pairwise nonadjacent under Q d ) S := collection of stable sets of Z 2 d

11. Let the group G of isometries of Z 2 d act on S by natural action of  ∈ G on stable set M ∈ S ie. α (M) = { α (m i ) |  m i ∈ M } orbit of M ∈ S is G M = { α ( M) |  α ∈ G } each orbit G M contains a set O M that contains the origin G M can be represented by O M Orbits of Stable Sets

12. Admissible Labelings of Z 2 d (3) means no two points in dom  are 2d-neighbors (3) and (4) imply that  (x) ≤ d-2  x ∈ dom 

13. Admissible Labelings of Z 2 d  1 ,  2 isomorphic if ∃ isometry Φ of Z 2 d onto Z 2 d s.t. dom  1 = Φ( dom  2 ) and  1 =  2 ( Φ ( dom  1 ) )   (0,1)-admissible labeling if  (x) ∈ { 0,1 } otherwise, non-(0,1)-admissible labeling

14. Correspondence isomorphism classes of admissible labelings of Z 2 d homeomorphism classes of digital topologies on Z d (Kong: using normalized admissible functions and digital strict partial orders) 1-1 correspondence

15. Find all orbit representatives O M of s table sets of Z 2 d For each O M , find admissible labelings  of Z 2 d wi th domain O M Kong's Algorithm

16. Counting Admissible Labelings We develop an algorithm to find and count all isomorphism classes of admissible labelings on Z 2 d count all (0,1)-admissible labelings count all non-(0,1)-admissible labelings

17. Results for Z 5 Lower bound for number of digital topologies for d=5

18. Further Work Get isomorphism classes of non-(0,1)- admissible labelings on Z 2 d Conjecture : upper bound for number of isomorphism classes of non-(0,1)- admissible labelings: Improve algorithm implementation Get number of digital topologies for higher dimensions (exact number or bounds)

19. References U. Eckhart and L. Latecki . Topologies for the Digital Spaces Z2 and Z3. Computer Vision and Image Understanding 90 (2003) 295-312. R. Klette and A. Rosenfeld . Digital Geometry. Morgan Kauffman Publishers. San Francisco, CA. 2004. T.Y. Kong . The Khalimsky Topologies are precisely those simply connected topologies on Zn whose connected sets include all 2n-connected sets but no (3n-1)-disconnected sets. Theoretical Computer Science 305 (2003) 221-235. T.Y. Kong . Topological adjacency relations on Zn. Theoretical Computer Science 283 (2002) 3-28. T.Y. Kong, R. Kopperman and P.R. Meyer . A Topological Approach to Digital Topology. Amer. Math. Monthly 98 (1991), 901-917. R. Kopperman . The Khalimsky Line as a Foundation for Digital Topology. Shape in Picture (Proceedings of the NATO Advanced Research Workshop held at Driebergen, Spet. 1992). Springer. 1994 V. Kovalevsk y. Axiomatische Digitaltopologie. http://www.bv.inf.tu-dresden.de/AKTUELL/S_KOLL_0406/VORTRAEGE/V1_Kovalevski.ppt. August 2006. G. Malandain . Digital Topology. http://www-sop.inria.fr/epidaure/personnel/malandain/topology/. August 2000. IMAGES: Open Problems by R.Klette . http://www.citr.auckland.ac.nz/dgt/Problem_Files/._Dagstuhl_2004.pdf Tesseract . http://en.wikipedia.org/wiki/Tesseract, http://en.wikipedia.org/wiki/Image:Changingcube.gif Penteract . http://mathworld.wolfram.com/images/eps-gif/HypercubeGraphs_850.gif

20. THANK YOU for listening! Any questions?? [email_address]