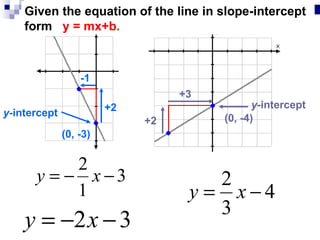
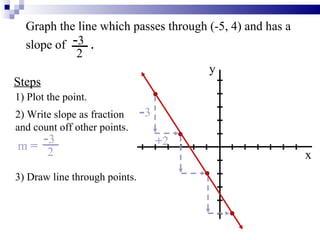
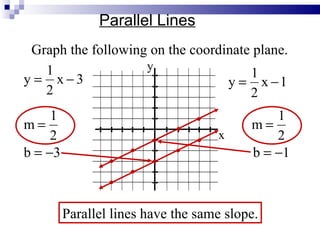
The document provides instructions for writing and graphing linear equations in slope-intercept form (y = mx + b). It defines key terms like slope (m), y-intercept (b), and parallel lines. Examples are given for writing equations from slope and y-intercept, graphing lines on a coordinate plane, and determining if two lines are parallel based on having the same slope. Key steps are outlined for graphing a line passing through a given point with a given slope.

1. Lesson 4.5 Goal: Write and graph linear equations using slope-intercept form of an equation. Question: How do you write and graph linear equations using slope-intercept form? .

2. Parallel lines have the same slope.

3. Slope Intercept Form y = mx + b “ m” is the slope (the ratio of rise to run) Slope is the change of y over the change of x. “ b” is the y-intercept (where the line crosses the y-axis)

4. Given the equation of the line in slope-intercept form y = mx+b. +2 -1 y- intercept (0, -3) +2 +3 y- intercept (0, -4)

5. +2 +1 y- intercept -3 +2 y- intercept (0, -2) (0, 3)

6. Finding the slope and y-intercept of a line. slope-intercept form m b slope y-intercept +2 +1 m = 2 -2 -1 y = 2x + 1

7. Example 1 y = mx + b 1 3 y 2x Add 2x + 5 2 5

8. Slope-Intercept Form of the Linear Equation Any linear equation which is solved for y is in slope-intercept form. y = mx + b Find the slope and y-intercept of the following linear equations: 1) y = 3x + 4 2) y = - 2x - 1 3) y = 5x 4) y = x - 4 5 8 5) y = x - - 2 9 1 4 6) y = 6 m = 3 b = 4 m = 2 b = - 1 m = 5 b = 0 m = b = - 4 5 8 m = b = - 2 9 - 1 4 m = 0 b = 6

9. slope: 4 y-intercept: -1 -4 x -4 x - 2 y = -4 x + 8 - 2 - 2 - 2 y = 2 x +-4 slope: 2 y-intercept: -4 4 4 4 y = ¾ x + 4 slope : ¾ y -intercept: 4 - 6 x -6 x 3 y = -6 x – 21 y = -2 x – 7 slope : -2 y -intercept: -7

10. Slope-Intercept Form of the Linear Equation Write a linear equation in the form y = mx + b given the following. 1) m = 2, b = -3 2) m = , b = 5 3) m = , y-int = 2 4) m = 0, b = 6 5) m = , b = 0 6) m = 1, b = y = 2x - 3 y = 6

11. Example 2 y = -4 x + 2 Identify -4 2 Plot 0, 2 -4 +1

12. Checkpoint y = ½ x + 1 y -intercept: 1 slope: ½

13. Graph the line which passes through (-2, 1) and has a slope of -3. x y 1) Plot the point. Steps 2) Write slope as fraction and count off other points. m = - 3 = - 3 1 - 3 + 1 or m = 3 - 1 3) Draw line through points.

14. Graph the line which passes through (3, 2) and has a slope of . x y 1) Plot the point. Steps 2) Write slope as fraction and count off other points. m = 3 4 + 3 + 4 or m = - 3 - 4 3) Draw line through points. 3 4

15. Graph the line which passes through (-5, 4) and has a slope of . x y 1) Plot the point. Steps 2) Write slope as fraction and count off other points. m = - 3 2 - 3 + 2 3) Draw line through points. - 3 2

17. Parallel Lines Graph the following on the coordinate plane. x y Parallel lines have the same slope.

18. Example 3 -3 -2 -6 -6 1 -2 -4 -6 -6 1 -5 -3 -7 -9 7 9 a b

19. Tell whether the lines below are parallel. 1) 3x + y = 7 y = -3x + 1 -3x -3x y = -3x + 7 m = -3 y = mx + b m = -3 Lines are parallel because they have the same slope ! Same slope!

20. Checkpoint Lines a and b are parallel. They have the same slope!