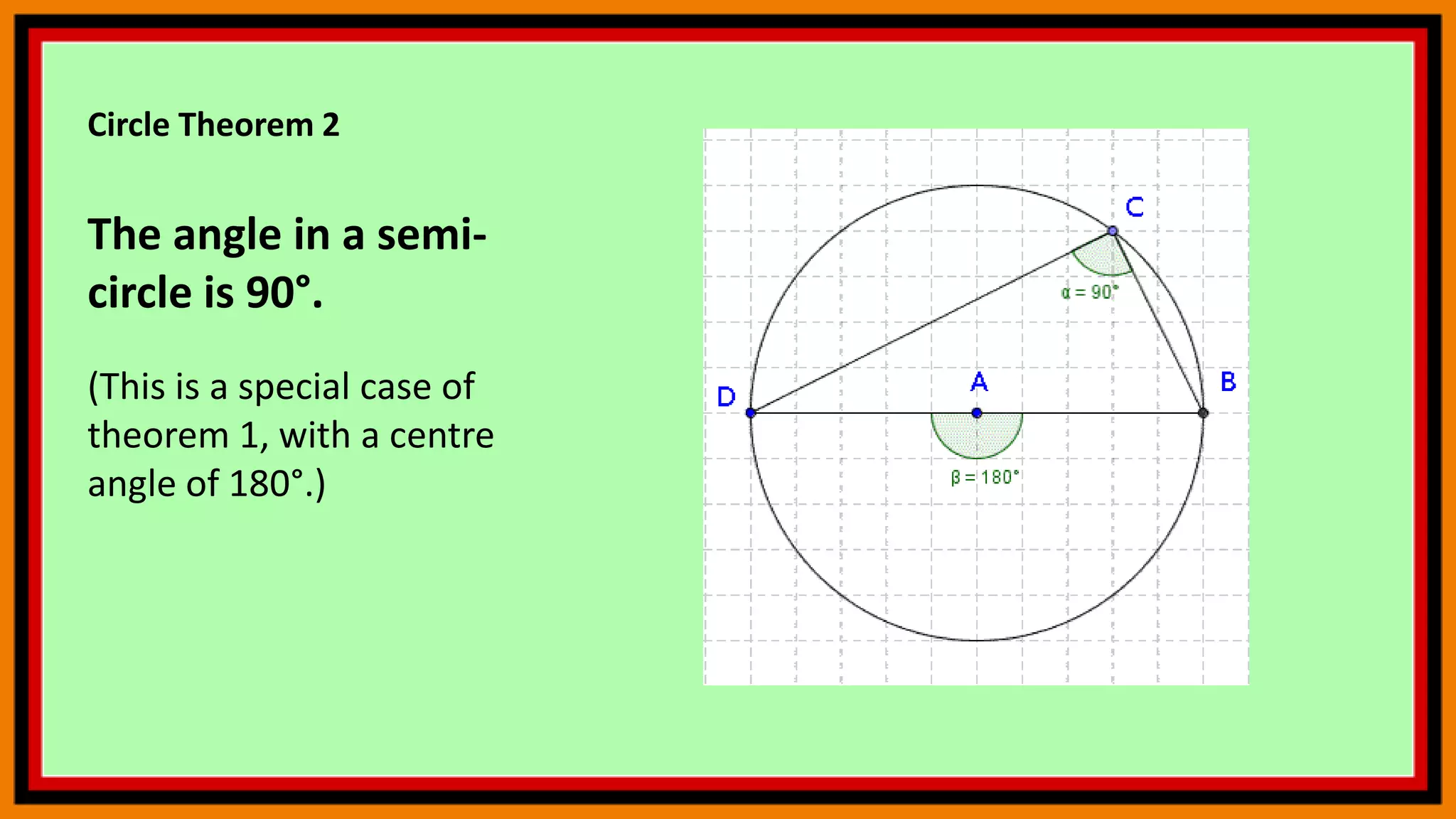
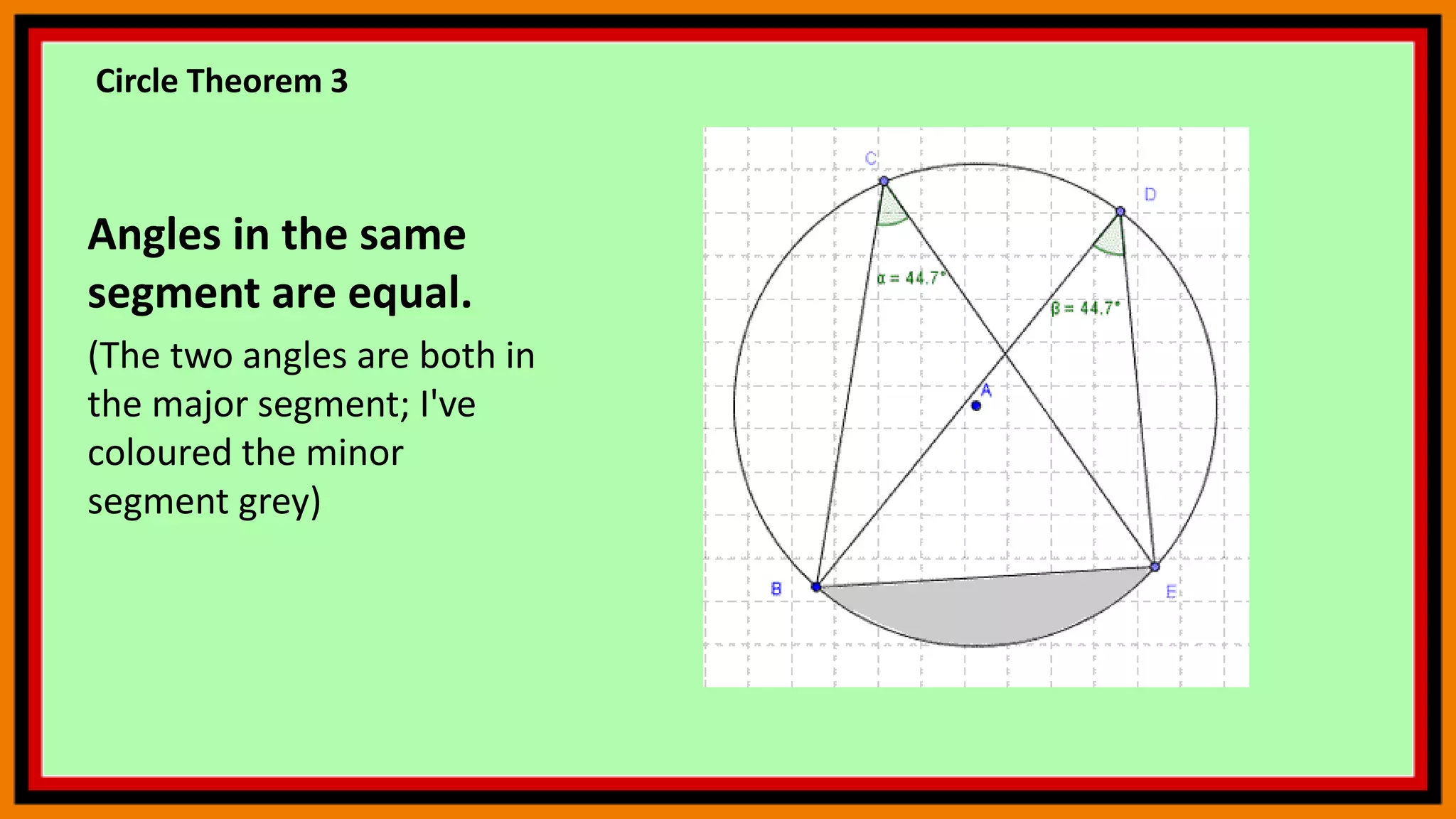
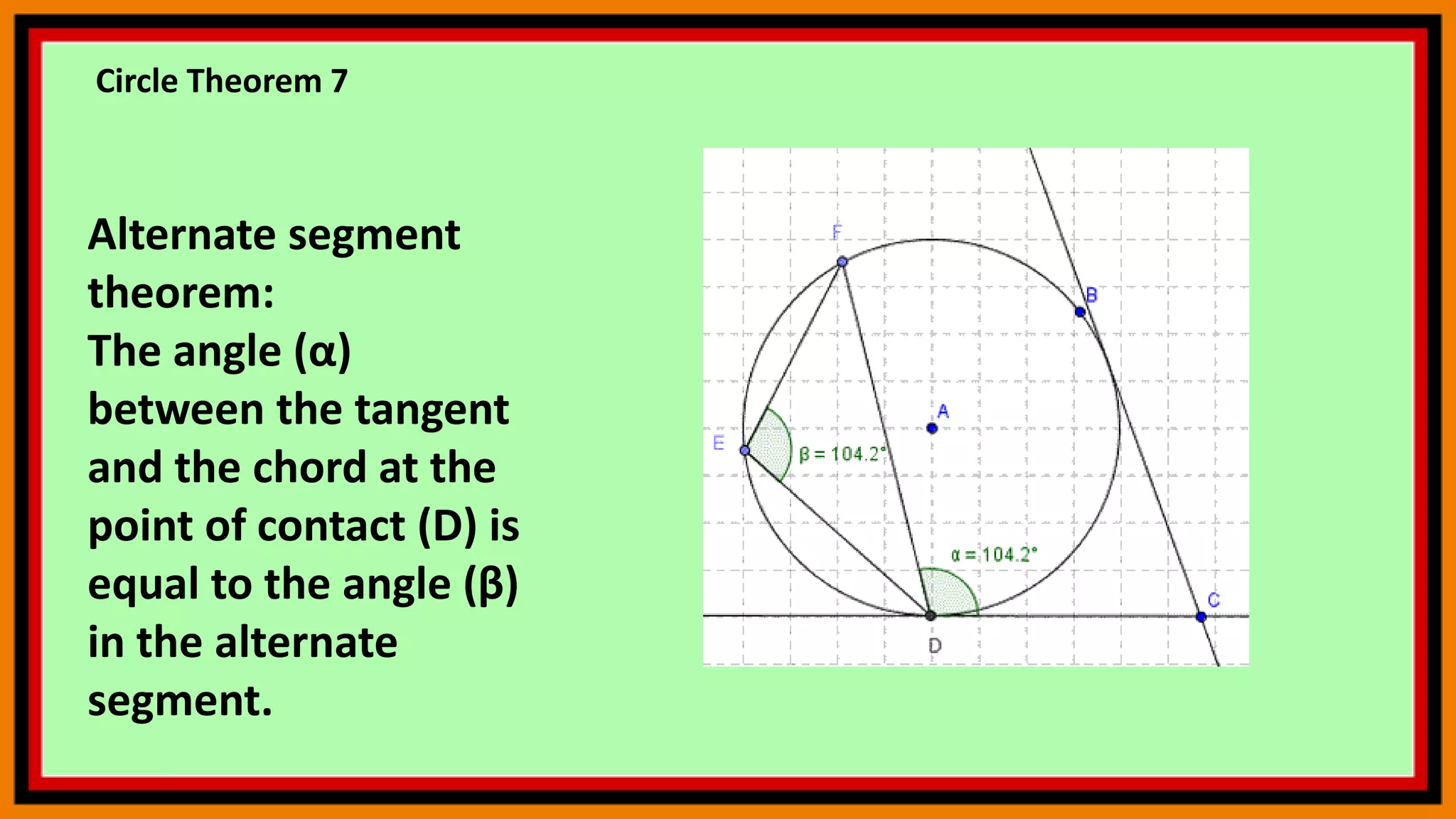
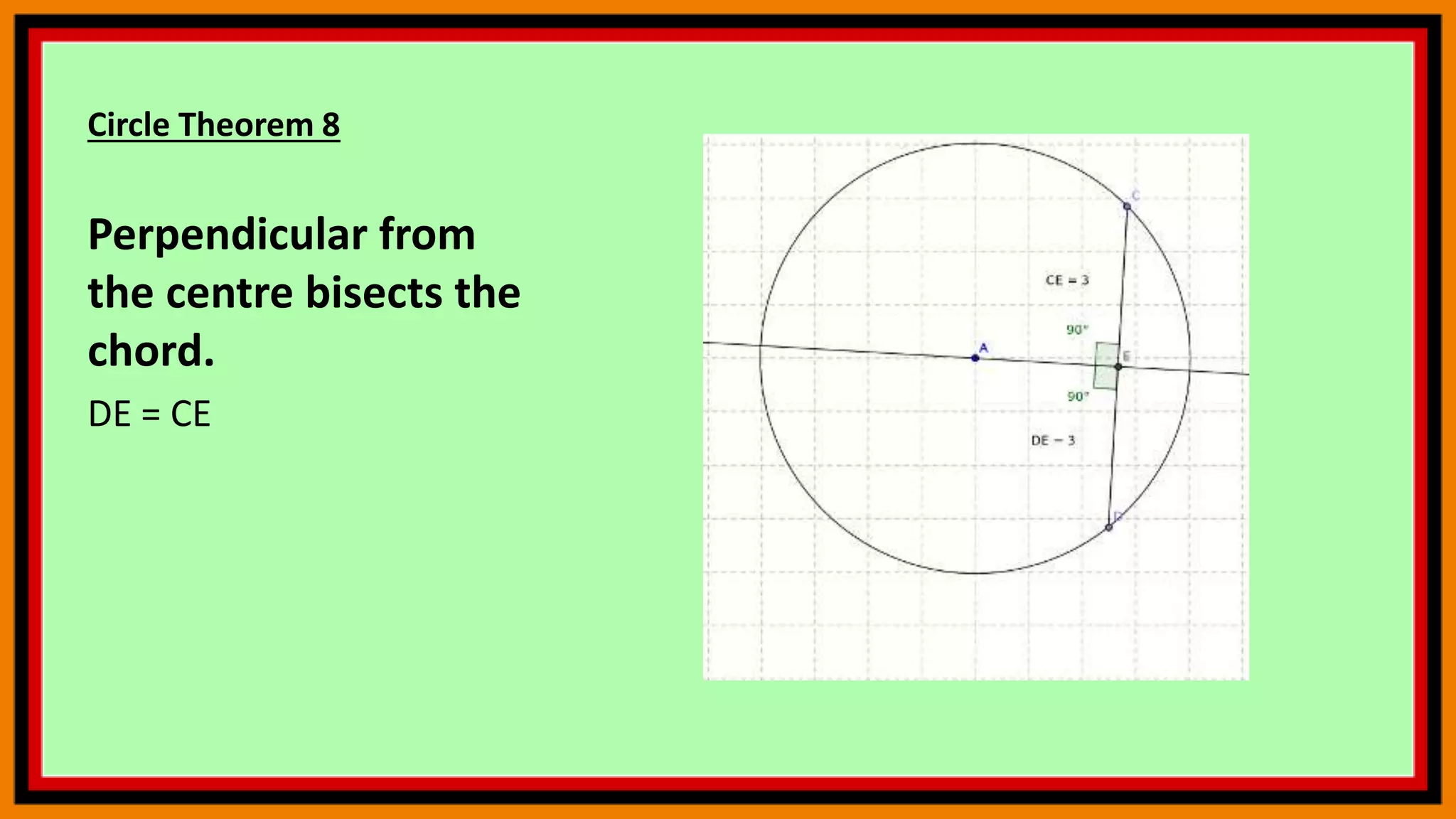
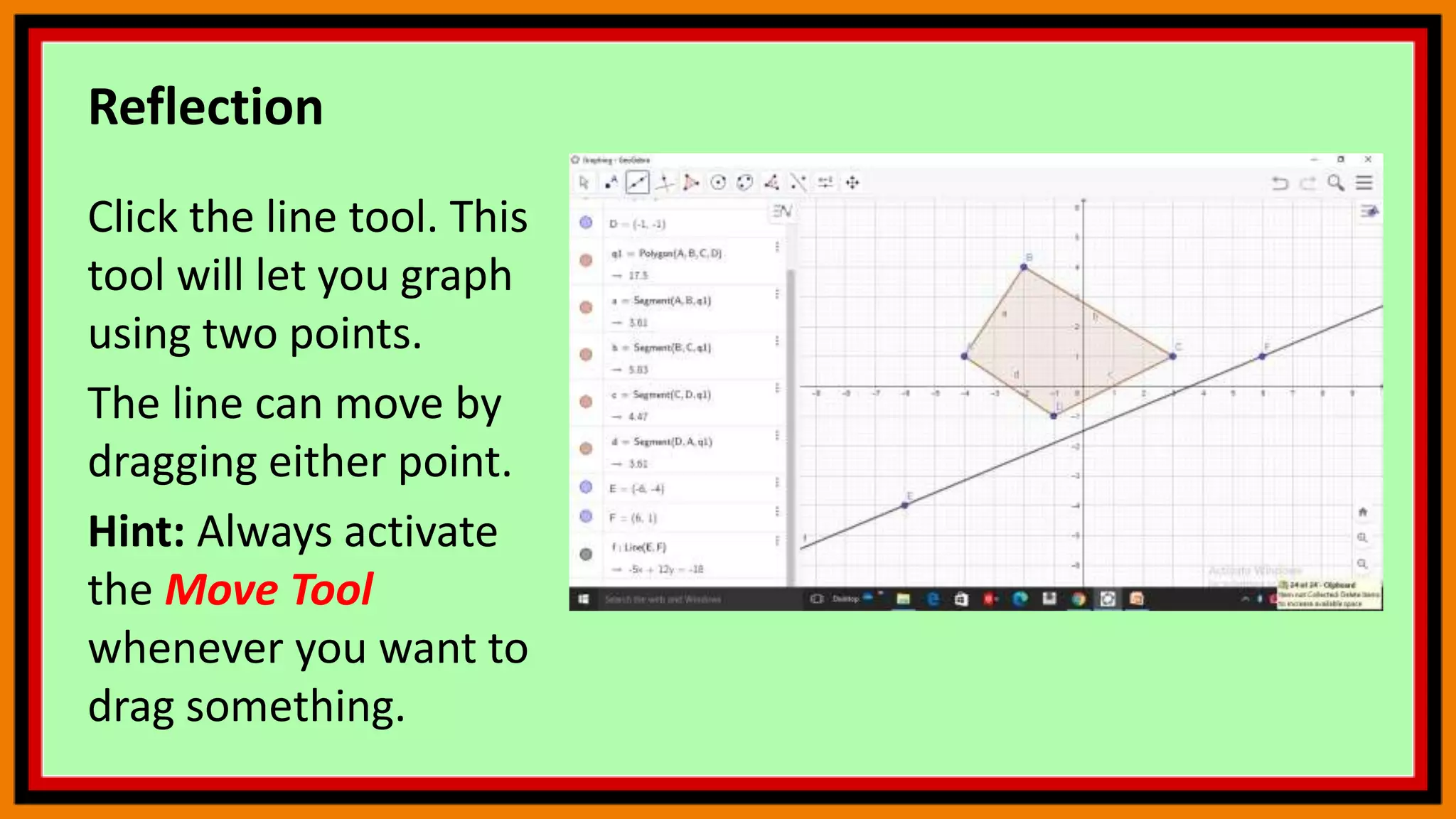
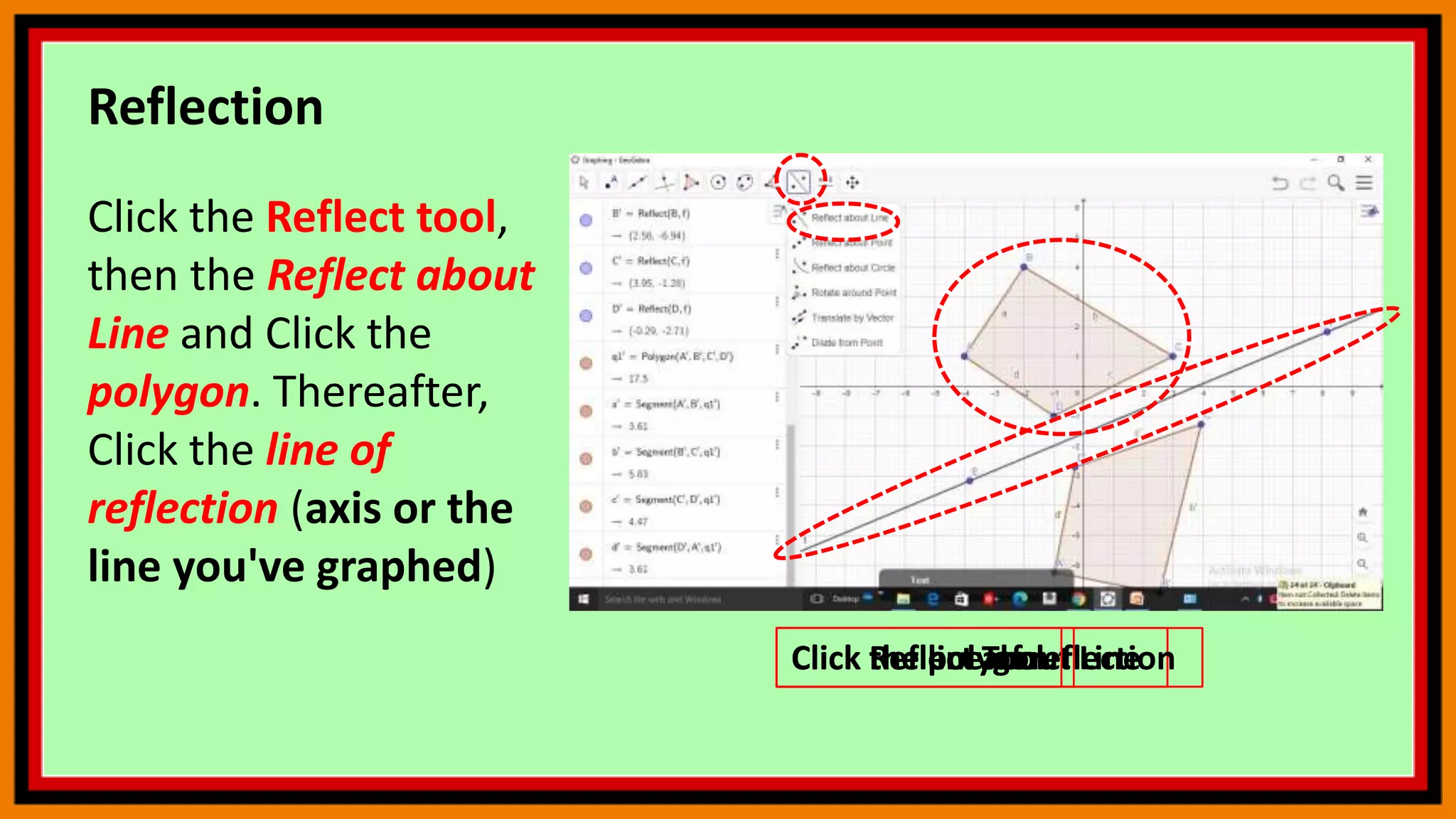
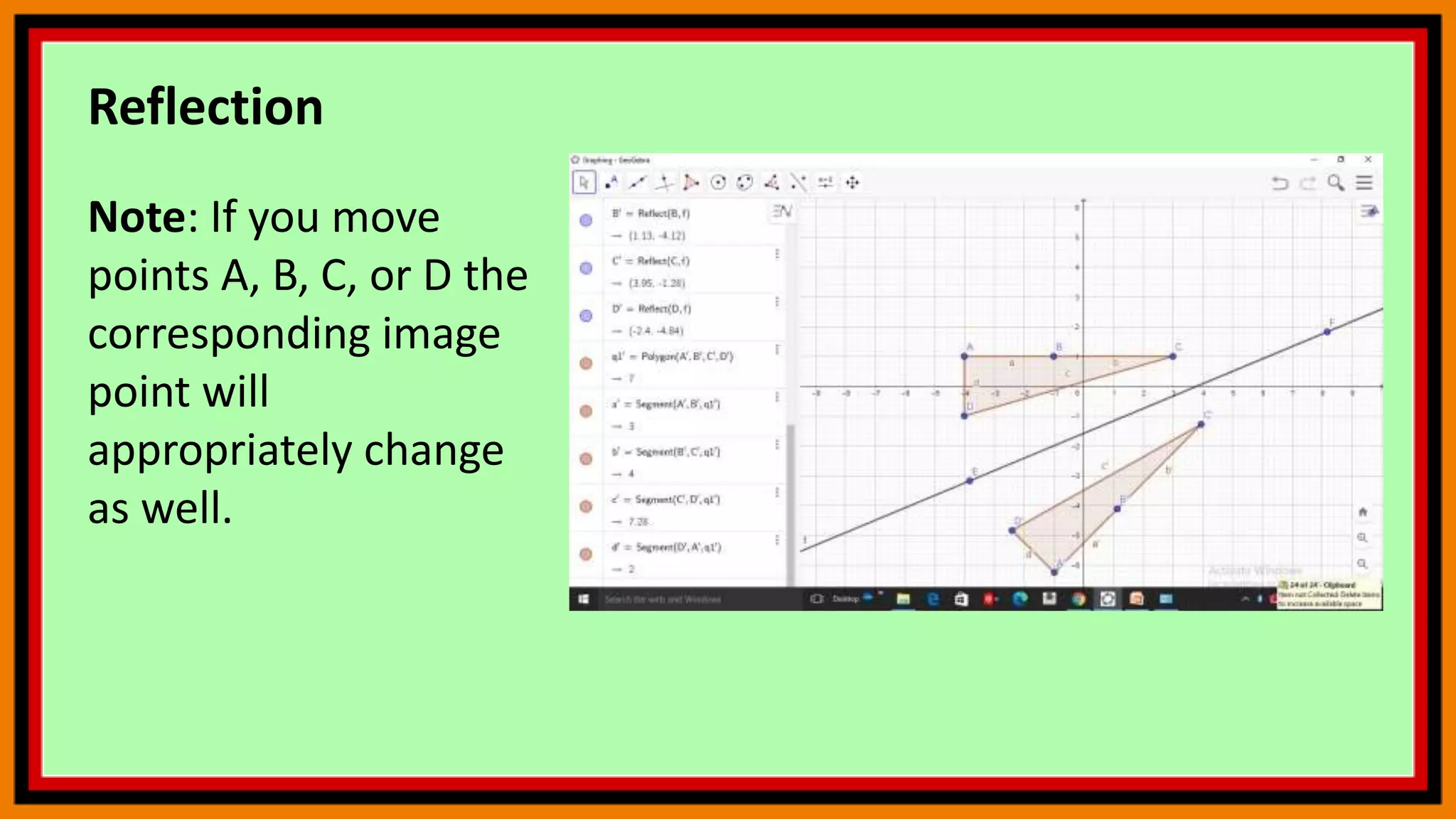
This document provides instructions for using geometry tools and concepts in GeoGebra. It includes sections on reflection, area under a curve using Riemann sums, circle theorems, and calculating angle sums in triangles. The reflection section demonstrates how to reflect polygons across lines. The area under a curve section shows how to calculate lower and upper Riemann sums and the actual integral. The circle theorems section lists several theorems without examples. The triangle section provides step-by-step instructions to construct a triangle, rotate it, and calculate interior angles and their sum. Users are encouraged to practice these concepts by following the commands.

1. Geometry Calculator

2. Contents
 Reflection
Area Under a Curve and Riemann Sums
Circle Theorems
Angle sum in a triangle

3. WARNING
Please always save your work in .ggb file
(GeoGebra format) as well as in any other
format of your choice. Saving in GeoGebra
format (.ggb)will enable you to use the same
file every time you want to visualize what you
earlier created without losing your work.

4. Reflection
Create a polygon with
the following
vertices A(-4, 1), B(-
2, 4), C(3, 1), and D(-1,
-1)

5. Reflection
Click the line tool. This
tool will let you graph
using two points.
The line can move by
dragging either point.
Hint: Always activate
the Move Tool
whenever you want to
drag something.

6. Reflection
Click the Reflect tool,
then the Reflect about
Line and Click the
polygon. Thereafter,
Click the line of
reflection (axis or the
line you've graphed)
Click Reflect about Line
Click the polygon
Click the line of reflection
Click Reflect Tool

7. Reflection
Note: If you move
points A, B, C, or D the
corresponding image
point will
appropriately change
as well.

8. Reflection
Do It Yourself
Try to plot the polygon
given and reflect
about the following
lines.
1. Line of Reflection:
x-Axis
2. Line of Reflection :
y=-1/2x +4

9. Area Under a Curve and Riemann Sums
Task
Visualize area under graph and given x-
coordinates

10. Area Under a Curve and
Riemann Sums
Open GeoGebra and
select Algebra and
Graphics from
the Perspectives menu

11. Area Under a Curve and
Riemann Sums
Graph f(x) = x2 by
typing f(x) = x^2 in the
Input bar and press
the ENTER key on your
keyboard
F(x) = x2

12. Area Under a Curve and
Riemann Sums
We now create a slider for
the number of rectangles.
Select the Slider tool and
click on the Graphics view.
In the Slider dialog box,
change the name to n, set
the minimum to 0,
maximum to 100, and
increment of 1, then click
the OK button. Change name to n
Set minimum to 0
Set maximum to 100
Click the OK button
Increment of 1

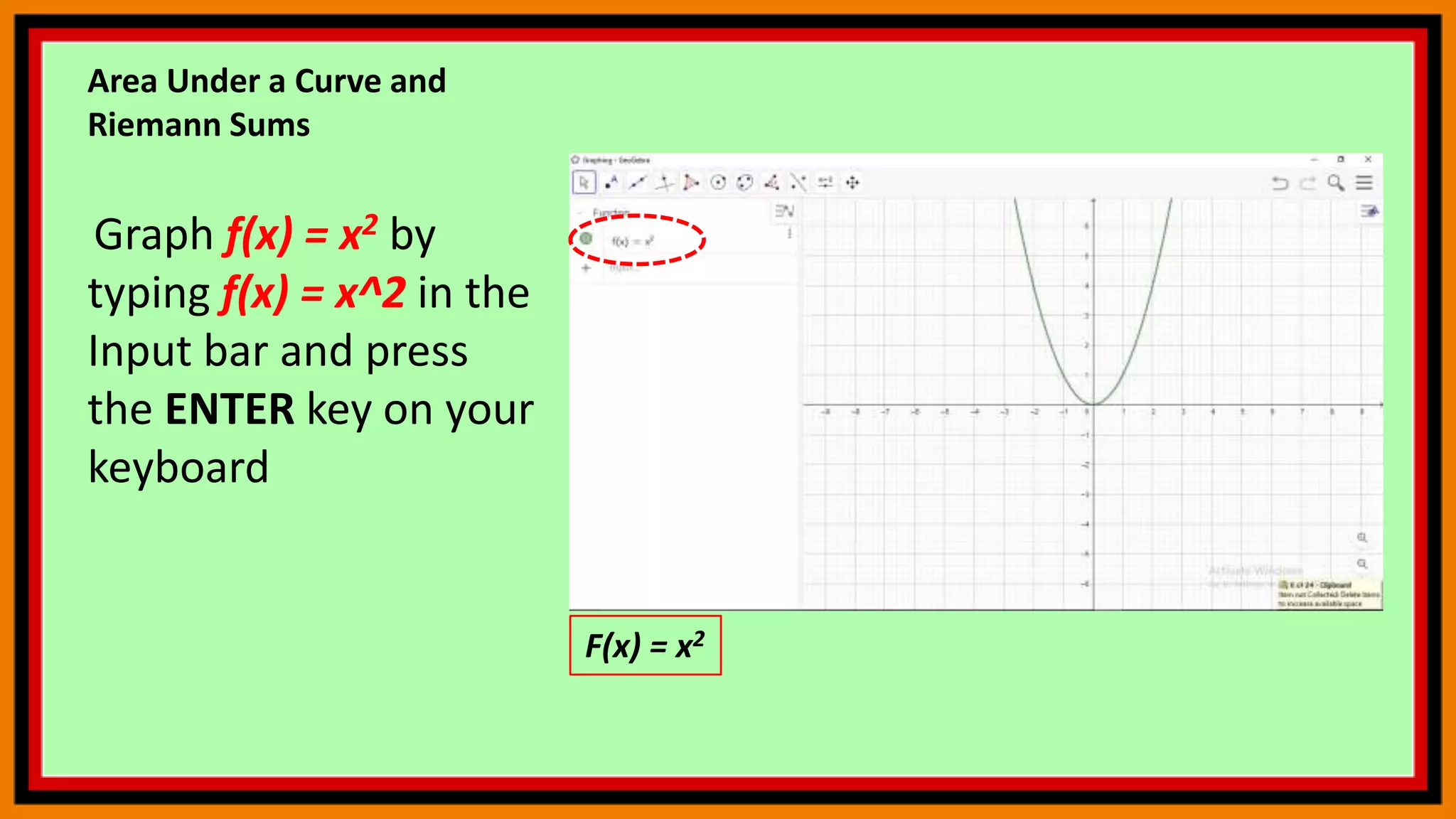
13. Area Under a Curve and
Riemann Sums
To construct the lower sum
(rectangles whose upper
left corners are on the
curve),
type lowersum[f,0,1,n] and
then press the ENTER key
on your keyboard. That is,
the lowersum (sum of the
areas of rectangles) under
the function f from 0 to 1
with n number of
rectangles.
LowerSum(f,0,1,n)

14. Area Under a Curve and
Riemann Sums
Move Slider n. What
do you observe?
Move n to the
extreme right. What is
the value of the lower
sum or the total area
of the rectangles
under the curve? Total Area = 0.33

15. Area Under a Curve and
Riemann Sums
To construct the upper
sum,
type uppersum[f,0,1,n
] in the drawing pad,
and press the ENTER
key.
upperSum(f,0,1,n)

16. Area Under a Curve and
Riemann Sums
Right click a (the value
of the lowersum) in
the Algebra window,
and click Settings to
show the
Preferences window.
Click Settings

17. Area Under a Curve and
Riemann Sums
In
the Preferences windo
w, select the Color tab,
choose a different
color, then press
ENTER and close
window. This will
make it easier to
distinguish the two
sums.
Click color tab
Choose a different color

18. Area Under a Curve and
Riemann Sums
Move the slider to
100. What do you
observe about the
values of the the
upper sum and the
lower sum?

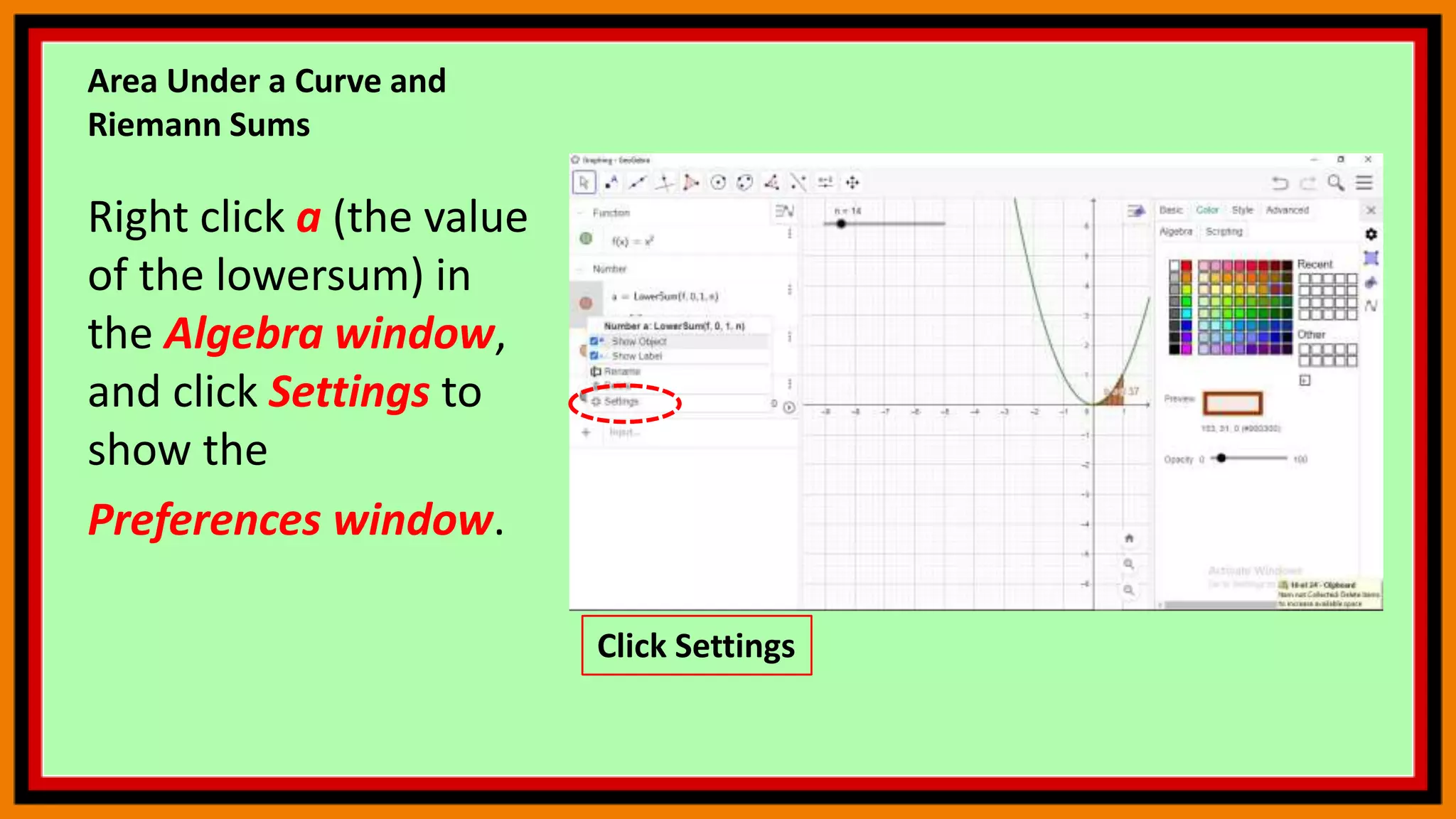
19. Area Under a Curve and
Riemann Sums
To get the actual area
under the curve, we
need the integral of
the function f from 0
to 1. To do this, type
integral integral[f, 0,
1] in the Input bar,
and press the ENTER
key.
Area under curve

20. Area Under a Curve and
Riemann Sums
Next, we construct a
check box that will
show/hide the three
objects. To do this,
select the Check
box tool and click
anywhere on
the Graphics view. Select Check Box
Caption text box appear

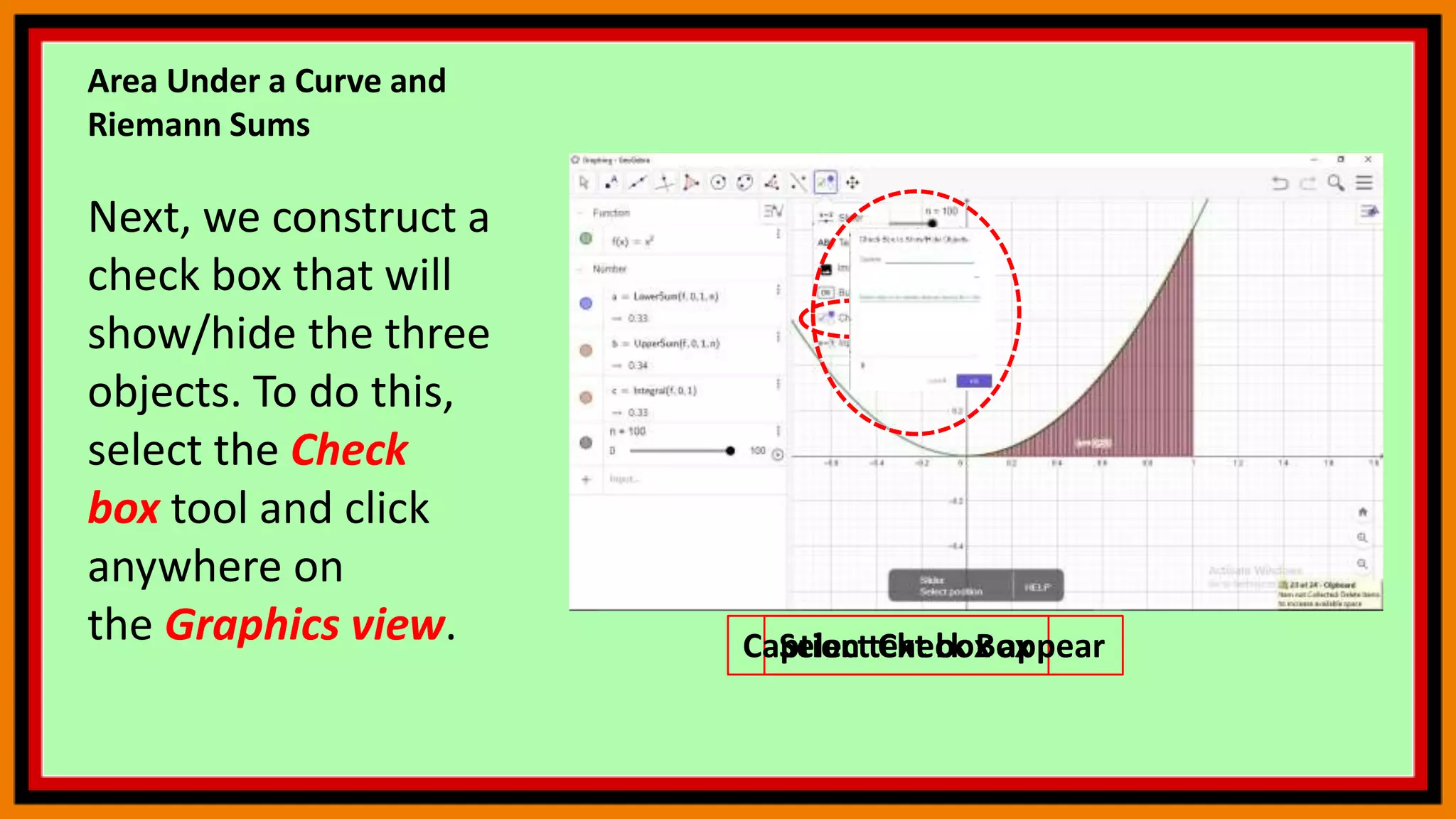
21. Area Under a Curve and
Riemann Sums
In the Caption text
box, type Show/Hide
Lower
Sum, select Number a:
Lower Sum[f,0,1,n] in
the Select
objects… box, and
then click the OK
button.
a: Lower Sum[f,0,1,n]
Click the OK button

22. Area Under a Curve and
Riemann Sums
Next, create two
more Show/Hide
Check boxes for the
Upper Sum and the
actual area (integral of
f from 0 to 1).
Check boxes

23. Area Under a Curve and
Riemann Sums
Try to change the
values of a: Lower
Sum[f,0,1,n] to a:
Lower Sum[f,0,3,n]
and b: Upper
Sum[f,0,1,n] to b:
Upper Sum[f,0,3,n].
What happens?
Change values here

24. Circle Theorems
Visualize the theorems shown in the following slides on your
own.

25. Circle Theorem 1
The angle at the
centre is twice the
angle at the
circumference.
(Note that both angles are
facing the same piece of
arc, CB)

26. Circle Theorem 2
The angle in a semi-
circle is 90°.
(This is a special case of
theorem 1, with a centre
angle of 180°.)

27. Circle Theorem 3
Angles in the same
segment are equal.
(The two angles are both in
the major segment; I've
coloured the minor
segment grey)

28. Circle Theorem 4
Opposite angles in a
cyclic quadrilateral
add up to 180°.

29. Circle Theorem 5
The lengths of the
two tangents from a
point to a circle are
equal.
CD = CE

30. Circle Theorem 6
The angle between a
tangent and a radius
in a circle is 90°.

31. Circle Theorem 7
Alternate segment
theorem:
The angle (α)
between the tangent
and the chord at the
point of contact (D) is
equal to the angle (β)
in the alternate
segment.

32. Circle Theorem 8
Perpendicular from
the centre bisects the
chord.
DE = CE

33. Angle sum in a triangle

34. Follow the instructions given to construct the given
Triangle
1.Create a triangle ABC with counter clockwise orientation.
2.Create the angles α, β and γ of triangle ABC.
3.Create a slider for angle δ with Interval 0 ̊ to 180 ̊ and
Increment 10 ̊.
4.Create a slider for angle ε with Interval 0 ̊ to 180 ̊ and
Increment 10 ̊.

35. Follow the instructions given to construct the given
Triangle
5.Create midpoint D of segment AC and midpoint E of segment
AB.
6.Rotate the triangle around point D by angle δ (setting
clockwise). Hint: Enter δ by using the Virtual Keyboard.
7.Rotate the triangle around point E by angle ε (setting counter
clockwise). Hint: Enter ε by using the Virtual Keyboard.
8.Move both sliders δ and ε to show 180 ̊.

36. Follow the instructions given to construct the given
Triangle
9.Create angle ζ using the points A’C’B’. Hint: To be sure to select
the right vertices change angle δ or use the command
angle(A’, C’, B’) instead.
10.Create angle η using the points C'1B'1A'1. Hint: To be sure to
select the right vertices change angle ε before or use the
command angle(C'1, B'1, A'1) instead.
11.Enhance your construction using the Style Bar. Hint:
Congruent angles should have the same color.

37. Follow the instructions given to construct the given
Triangle
12.Create dynamic text displaying the interior angles and their
values (e.g. enter α = and select α from the list of objects on
tab of the Advanced section).
13.Calculate the angle sum by entering sum = α + β + γ in the
Input Bar.

38. Follow the instructions given to construct the given
Triangle
14.Insert the angle sum as a dynamic text: α + β + γ = and select
sum from the list of objects on tab .
15.Match colors of corresponding angles and text using the Style
Bar.
16. Fix all texts that are not supposed to be moved by using the
Style Bar.

39. END
Try as many problems as possible. Practice
GeoGebra by following commands in the
GeoGebra Manual posted earlier.
Next: .