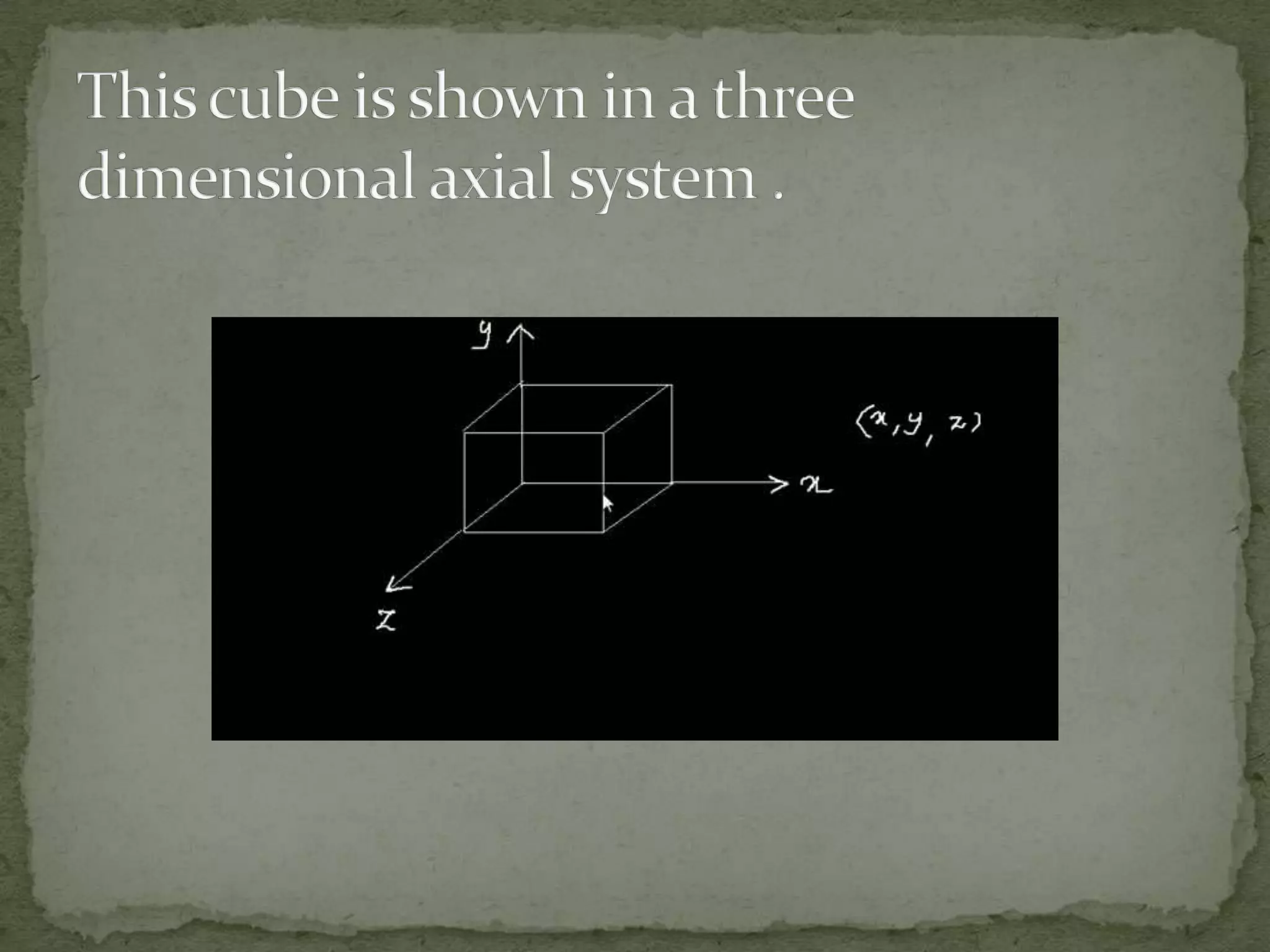
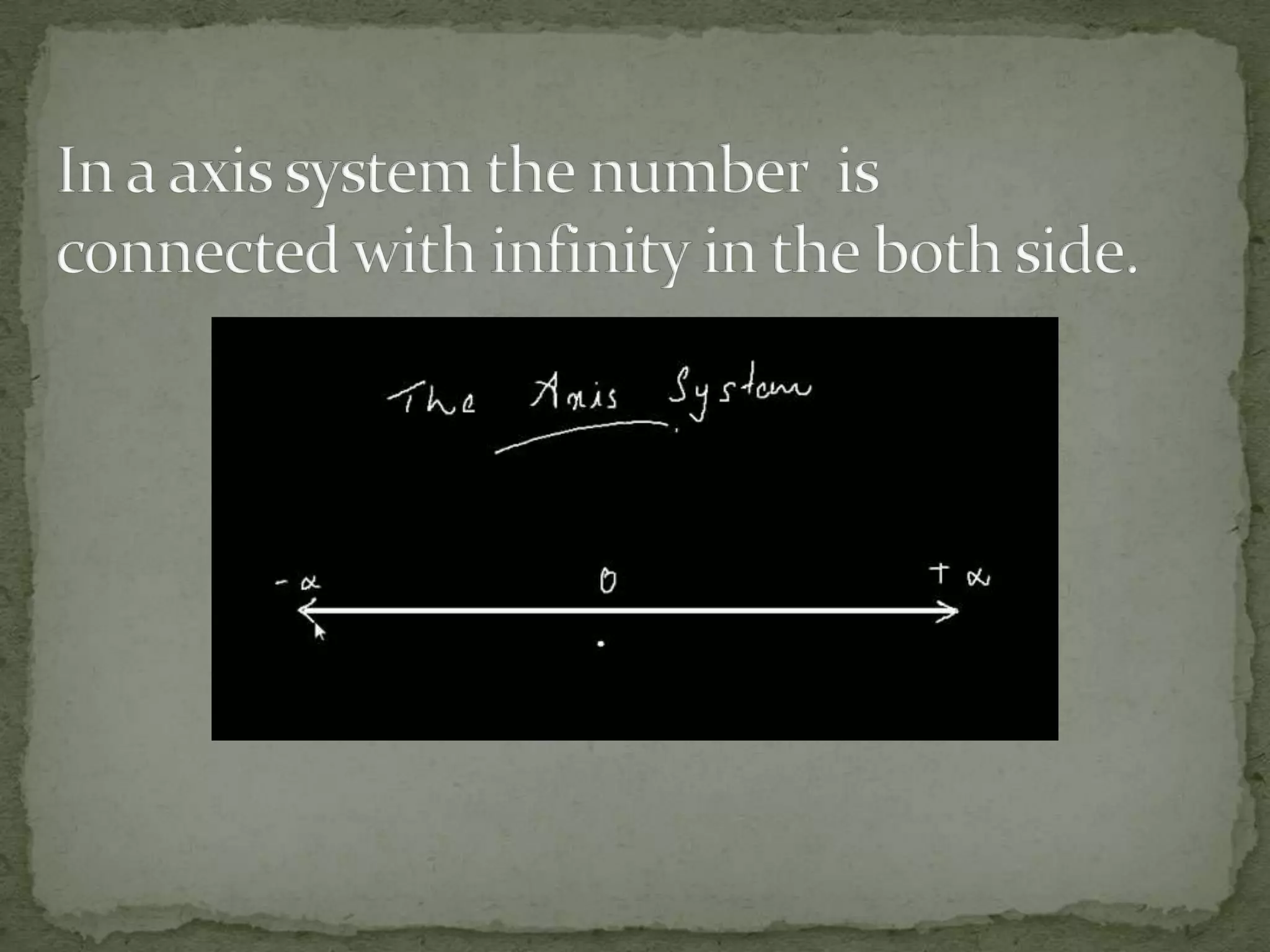This document discusses different coordinate systems including Cartesian, polar, cylindrical, and spherical coordinates. It explains that the Cartesian system uses perpendicular axes that intersect at right angles, with one point defined as the origin. Polar coordinates represent a point using its distance from the origin and the angle from the x-axis. The document also describes how the axial system is used to find distances between points and know positions relative to the axes in different dimensional systems.

1. Presentation on :
Axis System
MD. Rezaul hasan
Id : 10.01.03.111

2. 
The Cartesian coordinate system is the most commonly used
coordinate system. In two dimensions, this system consists of a pair of
lines on a flat surface or plane, that intersect at right angles. The lines
are called axes and the point at which they intersect is called
the origin.

9. In the figure below he Point P1 has polar coordinates (r1, f1) =
(5, 53.1o), and the point P2 has polar coordinates (r2, f2) = (3.16,
251.6o ).
The Transformation equations are:
x = r cosf, y = r sinf
r = (x2 + y2)1/2, f = tan-1(y/x)
Cylindrical coordinates and spherical coordinates are two
different extensions of polar coordinates to three dimensions.

10.  In a 3D Cartesian coordinate system, a point P is referred to
by three real numbers (coordinates), indicating the
positions of the perpendicular projections from the point
to three fixed, perpendicular, graduated lines, called
the axes which intersect at the origin. Often the x-axis is
imagined to be horizontal and pointing roughly toward the
viewer (out of the page), the y-axis is also horizontal and
pointing to the right, and the z-axis is vertical, pointing
up. The system is called right-handed if it can be rotated
so that the three axes are in the position as shown in the
figure above. The x-coordinate of of the point P in the
figure is a, the y-coordinate is b, and the z-coordinate is c

15.  Axial system is used to find the distance between two




point.
Use due to know the position of a number from 0 in
any dimensional system
Use for calculating slope in a straight line
Use for plotting graph
Measuring angle between two line intersecting each
other in any coordinate plane.
Etc.

16. THANK YOU