Chapter 3 of the document discusses multiple random variables and their statistical properties, including joint cumulative distribution functions, probability density functions, and the independence of random variables. It provides examples and methods for calculating the probability density function of sums of random variables and explores various scenarios involving independence and convolution. The chapter emphasizes the importance of understanding these concepts for practical applications, such as receiver design in communication systems.

1. Chapter 3: Multiple Random Variables
Addis Ababa Science & Technology University
Department of Electrical & Electronics Engineering
Probability and Random Process (EEEg-2114)

2. Multiple Random Variables
Outline
 Introduction
 The Joint Cumulative Distribution Function
 The Joint Probability Density and Mass Functions
 Marginal Statistics
 Independence
 Conditional Distributions
 Correlation and Covariance
 Functions of Two Random Variables
Semester-II, 2013/14 2

3. 3
One Function of Two Random Variables
Given two random variables X and Y and a function g(x,y),
we form a new random variable Z as
Given the joint pdf how does one obtain
the pdf of Z ? Problems of this type are of interest from a
practical standpoint. For example, a receiver output signal
usually consists of the desired signal buried in noise, and
the above formulation in that case reduces to Z = X + Y.
).
,
( Y
X
g
Z 
),
,
( y
x
fXY ),
(z
fZ
Semester-II, 2013/14

4. 4
It is important to know the statistics of the incoming signal
for proper receiver design. In this context, we shall analyze
problems of the following type:
The cdf of Z is given by:
)
,
( Y
X
g
Z 
Y
X 
)
/
(
tan 1
Y
X

Y
X 
XY
Y
X /
)
,
max( Y
X
)
,
min( Y
X
2
2
Y
X 
   
 





y
x
XY
Z
dxdy
y
x
f
z
Y
X
g
P
z
Z
P
z
F
,
,
)
,
(
)
,
(
)
(
)
( 
Semester-II, 2013/14

5. 5
Example -1: Let Z = X + Y. Find
Solution:
Since the required region in the xy plane where is
the shaded area shown below to the left of the line
Integrating over the horizontal strip along the x-axis first
(inner integral) followed by sliding that strip along the y-axis
from to (outer integral) we cover the entire shaded
area.
   










 ,
)
,
(
)
(
y
y
z
x
XY
Z dxdy
y
x
f
z
Y
X
P
z
F
z
y
x 

.
z
y
x 


 

y
z
x 

x
y
).
(z
fZ
Semester-II, 2013/14

6. 6
We can find by differentiating directly. In this
context, it is useful to recall the differentiation rule by
Leibnitz. Suppose
Then,
Using the above two equations, we get
Alternatively, the above integration can be carried out first
along the y-axis followed by the x-axis as below.
)
(z
FZ
)
(z
fZ


)
(
)
(
.
)
,
(
)
(
z
b
z
a
dx
z
x
h
z
H
     




)
(
)
(
.
)
,
(
),
(
)
(
),
(
)
(
)
( z
b
z
a
dx
z
z
x
h
z
z
a
h
dz
z
da
z
z
b
h
dz
z
db
dz
z
dH
( , )
( ) ( , ) ( , ) 0
( , ) .
z y z y
XY
Z XY XY
XY
f x y
f z f x y dx dy f z y y dy
z z
f z y y dy
   
   



  
 
    
   
 
   
 
   
 (i)
Semester-II, 2013/14

7. 7
In the second case
and differentiating the above
equation gives
 







 ,
)
,
(
)
(
x
x
z
y
XY
Z dxdy
y
x
f
z
F

 























.
)
,
(
)
,
(
)
(
)
(
x
XY
x
x
z
y
XY
Z
Z
dx
x
z
x
f
dx
dy
y
x
f
z
dz
z
dF
z
f
(ii)
If X and Y are independent, then
and inserting equation (iii) into equations (i) and (ii), we get
)
(
)
(
)
,
( y
f
x
f
y
x
f Y
X
XY 
.
)
(
)
(
)
(
)
(
)
( 













x
Y
X
y
Y
X
Z dx
x
z
f
x
f
dy
y
f
y
z
f
z
f
(iii)
(iv)
x
z
y 

x
y
Semester-II, 2013/14

8. 8
The above integral is the standard convolution of the
functions and expressed two different ways. We
thus reach the following conclusion: If two random variables
are independent, then the density of their sum equals the
convolution of their density functions.
As a special case, suppose that for and
for then we can use the following figure to determine
the pdf of Z.
)
(z
fX )
(z
fY
0
)
( 
x
fX 0

x 0
)
( 
y
fY
,
0

y
y
z
x 

x
y
)
0
,
(z
)
,
0
( z
Semester-II, 2013/14

9. 9
In the above case,
or
On the other hand, by considering vertical strips first in
above figure, we get
or
if X and Y are independent random variables.
 




z
y
y
z
x
XY
Z dxdy
y
x
f
z
F
0 0
)
,
(
)
(

















 
 



.
0
,
0
,
0
,
)
,
(
)
,
(
)
( 0
0 0
z
z
dy
y
y
z
f
dy
dx
y
x
f
z
z
f
z
XY
z
y
y
z
x
XY
Z










 
 

,
0
,
0
,
0
,
)
(
)
(
)
,
(
)
( 0
0
z
z
dx
x
z
f
x
f
dx
x
z
x
f
z
f
z
y
Y
X
z
x
XY
Z
 




z
x
x
z
y
XY
Z dydx
y
x
f
z
F
0 0
)
,
(
)
(
Semester-II, 2013/14

10. 10
Example-2: Suppose X and Y are independent exponential
r.vs with common parameter , and let Z = X + Y.
Determine
Solution: We have
and we can make use of (13) to obtain the pdf of Z = X + Y.
As the next example shows, care should be taken in using
the convolution formula for r.vs with finite range.
Example-3: X and Y are independent uniform r.vs in the
common interval (0,1). Determine where Z = X + Y.
Solution: Clearly, here, and as following
figure shows there are two cases of z for which the shaded
areas are quite different in shape and they should be
considered separately.
),
(
)
(
),
(
)
( y
U
e
y
f
x
U
e
x
f y
Y
x
X



 



2
0 



 z
Y
X
Z
),
(z
fZ
).
(
)
( 2
0
2
0
)
(
2
z
U
e
z
dx
e
dx
e
e
z
f z
z
z
z
x
z
x
Z






 






 

).
(z
fZ
Semester-II, 2013/14

11. 11
x
y
y
z
x 

1
0
)
( 
 z
a
x
y
y
z
x 

2
1
)
( 
 z
b
For
For notice that it is easy to deal with the unshaded
region. In that case
,
1
0 
 z
,
2
1 
 z
.
1
0
,
2
)
(
1
)
(
2
0
0 0





 
  



z
z
dy
y
z
dxdy
z
F
z
y
z
y
y
z
x
Z
 
.
2
1
,
2
)
2
(
1
)
1
(
1
1
1
1
)
(
2
1
1
z
1
1
1















 



 

z
z
dy
y
z
dxdy
z
Z
P
z
F
y
z
y y
z
x
Z
Semester-II, 2013/14

12. 12
Finally, differentiating the cdf, we obtain
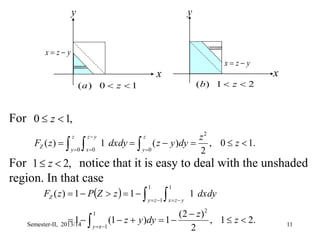
By direct convolution of and we obtain the
same result as above. In fact, for [Figure (a)]
and for [Figure (b)]
Figure (c) shows which agrees with the convolution
of two rectangular waveforms as well.










.
2
1
,
2
,
1
0
)
(
)
(
z
z
z
z
dz
z
dF
z
f Z
Z
)
(x
fX ),
( y
fY
1
0 
 z
2
1 
 z
.
1
)
(
)
(
)
(
0
z
dx
dx
x
f
x
z
f
z
f
z
Y
X
Z 


  
.
2
1
)
(
1
1
z
dx
z
f
z
Z 

  
)
(z
fZ
Semester-II, 2013/14

13. 13
)
(x
fY
x
1
)
( x
z
fX 
x
z
)
(
)
( x
f
x
z
f Y
X 
x
z
1

z
1
0
)
( 
 z
a
)
(x
fY
x
1
)
( x
z
fX 
x
)
(
)
( x
f
x
z
f Y
X 
x
1
1

z z
1

z
2
1
)
( 
 z
b
(c)
)
(z
fZ
z
2
0 1
Semester-II, 2013/14

14. 14
Example-4: Let Determine its pdf
Solution:
and hence
If X and Y are independent, then the above formula reduces
to
which represents the convolution of with
.
Y
X
Z 

   










 )
,
(
)
(
y
y
z
x
XY
Z dxdy
y
x
f
z
Y
X
P
z
F
( )
( ) ( , ) ( , ) .
z y
Z
Z XY XY
y x
dF z
f z f x y dx dy f y z y dy
dz z
  
  

 
   
 

 
  
( ) ( ) ( ) ( ) ( ),
Z X Y X Y
f z f z y f y dy f z f y


    

)
( z
fX  ).
(z
fY
y
x
z
y
x 

z
y
x 

y
).
(z
fZ
Semester-II, 2013/14

15. 15
As a special case, suppose
In this case, Z can be negative as well as positive, and that
gives rise to two situations that should be analyzed
separately, since the region of integration for and
are quite different. For from Figure (a)
and for from Figure (b)
After differentiation, this gives
 






0 0
)
,
(
)
(
y
y
z
x
XY
Z dxdy
y
x
f
z
F
 







0
)
,
(
)
(
z
y
y
z
x
XY
Z dxdy
y
x
f
z
F
.
0
,
0
)
(
and
,
0
,
0
)
( 


 y
y
f
x
x
f Y
X
0

z 0

z
,
0

z
,
0

z

















.
0
,
)
,
(
,
0
,
)
,
(
)
( 0
z
dy
y
y
z
f
z
dy
y
y
z
f
z
f
z
XY
XY
Z
(b)
y
x
y
z
x 

z

y
x
y
z
x 

z
z

(a)
Semester-II, 2013/14

16. 16
Example-5: Given Z = X / Y, obtain its density function.
Solution: We have
The inequality can be rewritten as if
and if
Figure (a) shows the area corresponding to the first term,
and Figure (b) shows that corresponding to the second term
in the above equation.
 .
/
)
( z
Y
X
P
z
FZ 

z
Y
X 
/ Yz
X  ,
0

Y
Yz
X  .
0

Y
y
x
yz
x 
(a)
y
x
yz
x 
(b)
     
   .
0
,
0
,
0
,
/
0
,
/
/













Y
Yz
X
P
Y
Yz
X
P
Y
z
Y
X
P
Y
z
Y
X
P
z
Y
X
P
Semester-II, 2013/14

17. 17
Integrating over these two regions, we get
Differentiation with respect to z gives
Note that if X and Y are nonnegative random variables, then
the area of integration reduces to that shown below
.
)
,
(
)
,
(
)
(
0
0  
  





 



y yz
x
XY
y
yz
x
XY
Z dxdy
y
x
f
dxdy
y
x
f
z
F
.
,
)
,
(
|
|
)
,
(
)
(
)
,
(
)
(
0
0




















z
dy
y
yz
f
y
dy
y
yz
f
y
dy
y
yz
yf
z
f
XY
XY
XY
Z
y
x
yz
x 
Semester-II, 2013/14

18. Exercise
The joint pdf of two random variables X and Y is given by:
Find the pdf of Z if :
otherwise
,
0
1
0
,
1
0
,
)
,
(


 





y
x
y
x
y
x
fXY
18
Y
X
Z
d
Y
X
Z
b
XY
Z
c
Y
X
Z
a






.
.
.
.
Semester-II, 2013/14

19. Assignment-III
1. Suppose that two continuous random variables X and Y have
joint pdf given by:
)
2
0
(
.
)
3
(
.
)
4
(
.
)
2
,
4
3
(
.
ies.
probabilit
following
the
Evaluate
.
.
and
of
pdf
l
conditiona
the
Find
.
t?
independen
and
Are
.
.
and
of
pdf
and
cdf
marginal
the
Find
.
.
and
of
cdf
joint
the
Find
.
.
constant
the
Find
.
constant.
a
is
re
whe
otherwise
,
0
5
0
,
6
2
,
)
2
(
)
,
(










 





Y
P
iv
X
P
ii
Y
X
P
iii
Y
X
P
i
e
Y
X
e
Y
X
d
Y
X
c
Y
X
b
k
a
k
y
x
y
x
k
y
x
fXY
Semester-II, 2013/14 19

20. Assignment-III Cont’d……
2. Let the joint pmf of two discrete random variables X and Y is
given by:
t?
independen
and
Are
.
.
and
of
pmf
marginal
the
Find
.
.
of
value
the
Find
.
constant.
a
is
re
whe
otherwise
,
0
2
,
1
3;
2,
,
1
,
)
(
)
,
(
Y
X
c
Y
X
b
k
a
k
y
x
y
x
k
y
x
P
i
j
i
j
i
XY


 



Semester-II, 2013/14 20

21. Assignment-III Cont’d…..
3. Suppose that two continuous random variables X and Y are
independent and uniform in the interval (0, 4).
Find the pdf of Z if :
.
.
.
.
.
X
Y
Z
e
XY
Z
d
Y
X
Z
c
X
Y
Z
b
Y
X
Z
a








21
Semester-II, 2013/14