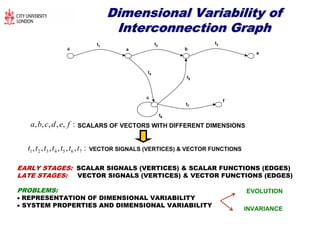
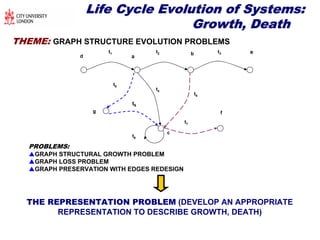
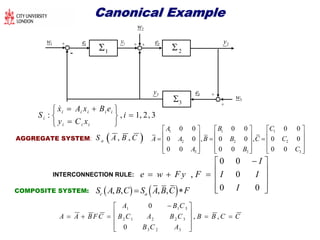
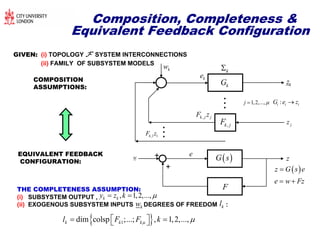
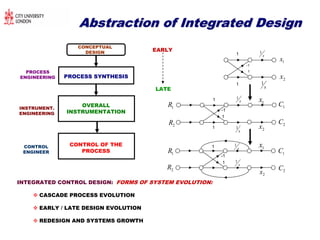
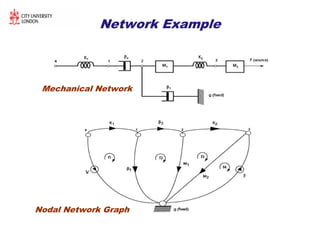
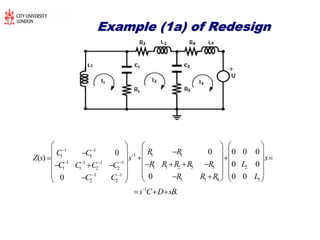
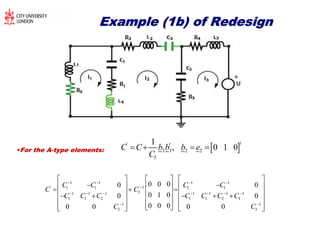
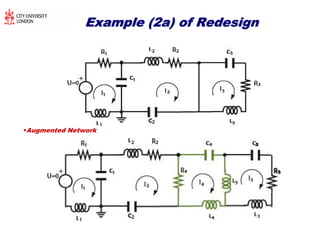
The document discusses structural transformations in passive electrical networks, focusing on redesigning components and their topologies to enhance dynamic behavior. It outlines various types of elements, the modeling of networks, and specifies challenges in network representation and transformation. The content emphasizes the importance of integrated design and control in evolving engineering processes related to energy systems and technology networks.

1. ““Structural Transformations of PassiveStructural Transformations of Passive
Electrical Networks and SystemElectrical Networks and System
PropertiesProperties””
Professor Nicos Karcanias
Athens, 17 January 2013
NTUA
Systems & Control Research Centre,
EEIE Department
School of Engineering & Mathematical Sciences

2. General Problem :ThemeGeneral Problem :Theme
TRADITIONAL CONTROL: THE SYSTEM IS ASSUMED FIXED
INTEGRATED SYSTEMS DESIGN: THE SYSTEM EVOLVES
THROUGH THE DIFFERENT DESIGN STAGES.
CONTROL AS INSTRUMENT IN GENERALISED DESIGN.
NEW PARADIGM: “STRUCTURE EVOLVING SYSTEMS”
SPECIAL CASE: “Passive Networks Redesign”

3. Evolution in Engineering ProcessesEvolution in Engineering Processes
Ad Hoc Networks
Operational
Embedding
Top-Down
Bottom-Up
Design
Stage
Evolution
EARLY
STAGES
LATE
STAGES
Design
Time
Evolution
▲ Integration of Design / Operations of
Technological Processes
▲ Power Generation & Distribution
Systems under Market De-regulation
▲ Networks of SYSTEMS: Control of
Communication/ Traffic Networks
▲ Re-Engineering of Technological
Processes

4. Abstraction of Integrated DesignAbstraction of Integrated Design
CONCEPTUAL
DESIGN
PROCESS SYNTHESIS
OVERALL
INSTRUMENTATION
CONTROL OF THE
PROCESS
EARLY
LATE
INTEGRATED CONTROL DESIGN: FORMS OF SYSTEM EVOLUTION:
 CASCADE PROCESS EVOLUTION
 EARLY / LATE DESIGN EVOLUTION
 REDESIGN AND SYSTEMS GROWTH
PROCESS
ENGINEERING
INSTRUMENT.
ENGINEERING
CONTROL
ENGINEER
1 1
s
1x
2x
-1
1
1 1
s
1R
2R
1
1
1
-1
2x
1x
1
s
1
s
1C
2C
1R
2R
1C
2C
-1
1
1
2x
1x1
s
1
s

5. Passive Network RedesignPassive Network Redesign
▲ GENERAL PROBLEM: Given a passive network define the
required changes in the nature of elements, values of
physical parameters and network topology required to
achieve a desirable dynamic behaviour.
Network Representation Problem: Admittance and Impedance
Operators (integral-Differential Operators)
Transformation Representation Problem: Describe
transformations of Network Reengineering
Network Redesign Problem: Develop and solve structure
assignment problems.

6. Classification of LampedClassification of Lamped
Physical ElementsPhysical Elements
• A-TYPE ELEMENTS: Translational mass; Inertia;
Electrical capacitance; Fluid capacitance; Thermal
capacitance
• T-TYPE ELEMENTS: Translational spring; Rotational
spring; Inductance; Fluid inertance
• D-TYPE ELEMENTS: Translational damper; Rotational
damper; Electrical resistance; Fluid resistance;
Thermal resistance

7. Network Example
Mechanical Network
Nodal Network Graph

8. Example: Loop Methodology
•• Impedance ModellingImpedance Modelling
1
1 1 1 2
3
1 1 2 1 1 2
1 1 2 2
1 1
( ) ( ) 0
0
1 1 1 1 1
( ) ( ) ( )
1 1 1
0 ( ) ( )
s f v
b k b f
f f
b b b m s m s m s
s
m s m s m s k
     
      
     
     
           
  
 
   
 
( ) ( )sf s v sZ (s) Impedance M r x: at iZ(s)

9. Example: Node Methodology
•• Admittance ModellingAdmittance Modelling
Adm ittance M atrix( ) :Y s
(b1  b2 
k1
s
) b2 0
b2 (m1s  b2 
k2
s
) (
k2
s
)
0 (
k2
s
) (m2s 
k2
s
)


















u1
u2
u3











k1
s
v
0
F












s( ) ( ) ( )Y s u s i s

10. The Vertex TopologyThe Vertex Topology

11. Components Vertex TopologyComponents Vertex Topology
• Component Topologies
1 2 2
2 2
0
0
0 0 0
b b b
b b
 
  
 
  
 
D= :Y D-type
1
2 2
2 2
0 0
0
0 -
k
k k
k k
 
 
 
 
 
 
 T= Y : T-type (1/s)
1
2
0 0 0
0 0
0 0
m
m
 
 
 
  
 
A= Y : A-type (s)
Boolean Symmetric matricesBoolean Symmetric matrices
defining the location of thedefining the location of the
physical elements in the Vertexphysical elements in the Vertex
Topology.Topology.
A A-Vertex TopologyY : A-typ A-Vertexe hGrap 
T T-Vertex TopologyY : T-typ T-Vertexe hGrap 
D D-Vertex TopologyY : D-typ D-Vertexe hGrap 

12. The Loop TopologyThe Loop Topology

13. Components Loop TopologyComponents Loop Topology
• Component Topologies
1 1
1 1 2
1/ 1/ 0
1/ 1/ 1/ 0
0 0 0
b b
b b b
 
 
  
  
 
D= Z : D-type
1
2
1/ 0 0
0 0 0
0 0 1/
k
k
 
 
 
 
 
 
T= Z : T-type (s)1 1
1 1 2
0 0 0
0 1/ 1/
0 1/ 1/ 1/
m m
m m m
 
 
 
    
A= Z : A-type (1/s)
Boolean Symmetric matricesBoolean Symmetric matrices
defining the location of thedefining the location of the
physical elements in the Loopphysical elements in the Loop
TopologyTopology
A A-Loop TopologyZ : A-ty A-Loope p Graph 
T T-Loop TopologyZ : T-ty T-Loopp phe Gra 
D D-Loop TopologyZ : D-ty D-Loopp phe Gra 

14. Admittance ModellingAdmittance Modelling
• is the sum of admittances in loop I
• is the sum of admittances common
between loops i and j
y11 y12 y13 ... y1n
y12 y22 y23  y2n
y13 y22 y33  y3n
   
y1q y2q y3q  ynn


















u1
u2
u3

un

















is1
is2
is3

isn
















yii (s)
yij (s)

15. Impedance ModellingImpedance Modelling
• is the sum of impedances in loop I
• is the sum of impedances common between
• loops i and j
11 12 13 1 1 1
12 22 23 2 2 2
13 22 33 3 3 3
1 2 3
... q s
q s
q s
q q q qq q sq
z z z z f v
z z z z f v
z z z z f v
z z z z f v
    
       
      
    
       
    
    
          


     

zii(s)
( )ijz s

16. System & Structural AspectsSystem & Structural Aspects
of Network Modelsof Network Models
• General Network
Operator
1
( )s s
s
  B CW D
Impedance, or Admittance OperatorImpedance, or Admittance Operator
W(s)is symmetric and the structure of B, C and D matricis symmetric and the structure of B, C and D matriceses
characterizes the topology of Acharacterizes the topology of A--, T, T-- and Dand D-- type matricestype matrices
associated with the network.associated with the network.
1
( )s s
s
  TA DY Y Y Y
1
( )s s
s
  AT DZ Z Z Z
Impedance OperatorImpedance Operator Admittance OperatorAdmittance Operator

17. AA--D & TD & T--D Networks, MatrixD Networks, Matrix
Pencils & RePencils & Re--engineeringengineering
• SPECIAL CASES: A-D and T-D Networks
1
ˆ ˆ( ) ( )s s s s
s
    A TW W D =CD CB D
ˆA TW (s), W (s) are symmetric structured matrix penare symmetric structured matrix pencils andcils and
the structure of B, C and D matrices characterizes thethe structure of B, C and D matrices characterizes the
topology of Atopology of A--, T, T-- and Dand D-- type matrices associated with thetype matrices associated with the
network. Furthermore, passivity of the network impliesnetwork. Furthermore, passivity of the network implies
stabilitystability
PROBLEM:PROBLEM: Define the properties of the spectrum of theDefine the properties of the spectrum of the
pencils underpencils under structural transformationsstructural transformations inin
the corresponding networkthe corresponding network
( ), ( )s sTAW W

18. Basics of Network TopologyBasics of Network Topology
• Remark: The presence of an element of A-, T- or D-type
is expressed by an entry in the corresponding matrix
C, B or D, respectively. In particular,
• (i) if an element is present in the i-th loop (node), then
its value is added to the (i, i) position of the respective
matrix.
• (ii) if an element is common to the i-th and j-th loop
(node), then its value is added to the (i, i) and (j, j)
positions, as well as subtracted from the (i, j) ) and
(j, i) positions of the corresponding matrix.
• Structured elementary matrices expressing addition,
or elimination of network elements without altering
the cardinality of the respective graph.

19. The RC, RL Matrix PencilThe RC, RL Matrix Pencil
•• PROPERTIES OF THE RC, OR RL NETWORK OPERATORPROPERTIES OF THE RC, OR RL NETWORK OPERATOR
[ ]s



 
kxk
t t
sF + G
(sF + G) (sF + G) 0 F G 0
F = F 0, G = G 0
Given the network pencil we have the following properties :
(i) is regular, ie det and ker{ } ker{ } = { }
(ii) and all eigenvalues are real and non - posi
1 1fk  


  
}
}
:kxk
1
1,
sF + G
sF + G (sF + G) F
F G 0 T 0
tive
(iii) All finite eigenvalues are real and index{
(iv) If index{ then deg{det } = rank{ }
(v) If ker{ } ker{ } = { }, and diag{ },,..., 
0
{ } fk k k
t
T sF + G T = sI + sI sIblock - diag{ }  

20. Passive Networks Redesign
Problem
PROBLEM: CHANGE PERFORMANCE OF PASSIVE NETWORKS BY REDESIGN
 CHANGE VALUES OF COMPONENTS
 ALTER NATURE OF COMPONENTS
 MODIFY EXISTING TOPOLOGY BY REDUCING THE SYSTEM, EXISTING STRUCTURE
 AUGMENT THE SYSTEM BY ADDING SUBSYSTEMS AND EVOLVING EXISTING
TOPOLOGY
CASE (i): DETERMINE THE RESISTORS IN AN RL NETWORK
IMPEDANCE MATRIX:  1 2Q sL + R Q + D
Diagonal design
parameters
CASE (ii): DETERMINE THE RESISTORS IN AN RLC NETWORK
IMPEDANCE MATRIX:   t t
1 1 2 2
1Q sL + R + Q + Q DQ
sC
PROBLEMS ARE REDUCED TO DETERMINANTAL ASSIGNMENT

21. Example (1a) of RedesignExample (1a) of Redesign
1 1
1 111 1
1 1 1 1
1 1 2 3 3 21 1 2 2
1 1
3 3 4 32 2
1
0 0 0 00
( )
0 0
0 0 00
.
R RC C
Z s s s
R R R R R LC C C C
R R R LC C
s C D sB
 

   
 

     
     
                  
           
  

22. Example (1b) of RedesignExample (1b) of Redesign
 '
3 3 2 2
3
1
, 0 1 0
tt
C C b b b e
C
   
1 1 1 1
' 11 1 1 1
31 1 1 1 1 1 1
1 1 2 1 1 2 3
1 1
3 3
0 0 00 0
0 1 00 0
0 0 00 0 0 0
C C C C
C C
C C C C C C C
C C
   

      
 
     
                 
     
        
For the A-type elements:

23. Example (1c) of RedesignExample (1c) of Redesign
 For the D-type elements:
 '
5 1 1 1 1, 1 0 0
tt
D D R b b b e   
1 1 5 1 5 1'
1 1 2 3 3 1 1 2 3 3
3 3 4 3 3 4
0 0 0 0
0 0 0
0 0 0 0 0
R R R R R R
D
R R R R R R R R R R
R R R R R R
     
                     
     
           
For the T-type elements:
'
4 12 12 12 1 2,t
B B L b b b e e   
1 4 4 1 4 4'
4
2 4 4 4 2 4
3 3
1 1 0 0 0 0 0
1 1 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
L L L L L L
B B L
L L L L L L
L L
       
                        
       
            

24. Example (2a) of RedesignExample (2a) of Redesign
Augmented Network

25. Example (2b) of RedesignExample (2b) of Redesign
1 1 1
1
1 1 2 2
4 4 5 5
3 5 3 5
1
1
2 4 4
4 4
3
1/ 1/ 0 0 0 0 0
( ) 1/ 1/ 1/ 0 0 0 0 0
0 0 1/ 0 0 0
0 0 0 1/ 0 0
0 0 0
0 0
0 0
0 0 0
C C L
Z s C C C s L s
C L L L
C L L L
R
R R R s C sB D
R R
R


   
   
       
   
    
       
 
 
      
 
 
 
 
.
Augmented Impedance: Column-Row Expansion

26. AA--D & TD & T--D Networks: singleD Networks: single
Parameter PerturbationsParameter Perturbations
• PROBLEM: [ ]s

kxk
'
sF + G
F F + F(x,b), G = G + G(x,b),
F(x,b),G(x,b) = xbb
Given investigate the effect
of perturbations on the pencil of the type :
where
, , 


t
i i jb = e b = e e
f(s,F,G, x,b)= det(s(F + F(x,b))+ G)
f(s,F
or
Study the determinantal assignment problems
,G, x,b)= det(sF + G + (G(x,b))

27. The Network CharacteristicThe Network Characteristic
PolynomialPolynomial (a)(a)
• Problem Formulation: Binet-Cauchy Theorem




( )
[ ]

i
i j
k
k
-k b = e
b = e e
f(s,F,G, x,b)= det s(F + F(x,b))+ G =
I
= det sF + G, I
sF(x,b)
(second order
(firs
variatio
node or loop graph a t order variation)nd or
n)
Assume :
   2k
k
2k1
k
x

 

 
  
 
[ ]
t
kt
k k k
g(s,F,G) p(s, x,b)
I
g(s,F,G) = C sF + G, I , p(s, x,b) = C
sF(x,b)
g(s,F,G) :
p(s, x,b) : Grass
Grassmann vector of
mann vector of the
the netw
structu
ork
ralperturbation

28. The Network CharacteristicThe Network Characteristic
PolynomialPolynomial (b)(b)
• Lemma: Grassmann vector of Structural Perturbation
, ,
( )=( , ( )
i
sx
sign

    
  

    

k,2k
[ ],
) Q
( ) ( ) ( )
j
1,0,..,a 0,...,0 a
1,.., -1, +1,k,...k+
b= e
b=
p(s,x,b),
p s,x,e =
p(s,x,b)e e
firstorder variation
secondorder varia
hasthestructure:
tion : ha-
:
1 2 3 4,
( ) , r= ( )
( )=( , ( )=(
i
r
j j i j j j
r sx r
   
  
 
 
k,2k
[ ]
) Q
( ) , , ,j ( ) ( ) ( ) ( )
( )
1,0,..,a 0,...,0,a 0,...,0,a 0,...,0,a 0,...,0
a 1,2,3,4 1
1 1,2,.., -1, +1,...,k,k+ 2 1,2,.., -1, +1,...,k,k+
p s,x,e e =
sthestructure:
-
,
( )=( , ( )=(i i i i j 

 
k,2k
k,2k k,2k
) Q
) Q ) Q3 1,2,..,i -1, +1,...,k,k+ 4 1,2,.., -1, +1,...,k,k+

29. The Network CharacteristicThe Network Characteristic
PolynomialPolynomial (c)(c)
• LEMMA: GRASSMANN VECTORS OF STRUCTURAL
PERTURBATIONS
, ,
( )=( , ( )
i
sx
sign

    
  

    

k,2k
[ ],
) Q
( )
firstorder variation
secondorder
hasthestructure:
variation ha:-
:
( ) ( )
j
1,0,..,a 0,...,0 a
1,.., -1, +1,k,...k+
p(s,x,b),
p s,x,e =
p(s,
b= e
b= e e x,b)
1 2 3 4,
( ) , r= ( )
( )=( , ( )=(
i
r
j j i j j j
r sx r
   
  
 
 
k,2k
[ ]
) Q
( ) , , ,
sthestructure:
- j ( ) ( ) ( ) ( )
( )
1,0,..,a 0,...,0,a 0,...,0,a 0,...,0,a 0,...,0
a 1,2,3,4 1
1 1,2,.., -1, +1,...,k,k+ 2 1,2,.., -1, +1,...,k,k+
p s,x,e e =
,
( )=( , ( )=(i i i i j 

 
k,2k
k,2k k,2k
) Q
) Q ) Q3 1,2,..,i -1, +1,...,k,k+ 4 1,2,.., -1, +1,...,k,k+

30. RC, RL Single Variations asRC, RL Single Variations as
Root Locus ProblemRoot Locus Problem
•• THEOREM:THEOREM: ROOT LOCUS FOR RC, RL SINGLE PARAMETER
VARIATIONS: The network characteristic polynomial is
expressed as:
( ) ( )
+) ( )(
s s
ss


and is formed from the nonzero compon
first order variation
ents of
according to the rules
(i)
F,G F,G,b
F, F,G,bG
p det(sF + G)
p(s,
b =
x,b)
e
f(s,F,G, x,b) =
z
p xsz
4
1
( ) ( ) ( ), ( )
( )= (
( )i
s s s
s
  

 
  
 
 




 
k,2k) Q
where is the
component of that corr
second order variation
esponds to
(ii :) -
: F,G,b F,G, F,G,
F,G,bj F,G,
( )
1, .., - 1, + 1,k, ...k +
b = e e
p(s, x,b)
z z z a
z z

( )
( )
( )= ( , ( )= (j j i j j j
s
s
  k,2k k) Q ) Q
where are the components of that corresponds to the sequences
characterising the nonzero elements ie
F,G,
1 1,2, .., - 1, + 1, ...,k,k + 2 1,2, .., - 1, + 1, ...,k,k +
p(s, x,b)z


,
( )= ( , ( )= (i i i i j  
,2k
k,2k k,2k) Q ) Q3 1,2, ..,i - 1, + 1, ...,k,k + 4 1,2, .., - 1, + 1, ...,k,k +

31. Root Locus & Fixed ModesRoot Locus & Fixed Modes
• CROLLARY: FIXED MODES OF THE SINGLE VARIATION PROBLEM:
( ) ( ) ( ),
( )
( )
s s s
s
 
 
 
Thepolynomial has a fixedmodeiff :
(i) and
where is the component of that corr
first order variatio
esponds to
n : F,G F,G,b F,G,
F,G,
p det(sF +b = e G)
p(s,x,b)
f(s,F,G,x,b)
z z
z
= (
( )
( ),
i s
s
   

k,2k) Q
secondord
have anontrivialgcd.
(ii) andthe set of
polynomials = which are the compon
er variati
entso
on
f
:- F,Gj
F,G,
1,.., - 1, + 1,k,...k +
1,2,3,4
b = e e p det(sF +G)
p(s,xz 

( )= ( ,
( )= ( , ( )= ( ,
( )= (
j j i
j j j i i
i i j

 


 

k,2k
k,2k k,2k
k,2k
) Q
) Q ) Q
) Q
correspondingto the sequences:
have a
1 1,2,.., -1, + 1,...,k,k +
2 1,2,.., -1, + 1,...,k,k + 3 1,2,..,i -1, + 1,...,k,k +
4 1,2,.., -1, + 1,...,k,k +
,b)
nontrivialgcd.

32. Properties of Root LocusProperties of Root Locus
ROOT LOCUS STRUCTURE AND PROPERTIES
+ 0( ) ,
( )
( )
:( ):
ss
s s
F,G,F,G
F,G
b
F,G,b
Characte xsristic Equation: p
sp
z
zpolepolynomial, zeropolynomial
For RC,or RLnetworks withfirst,or secondorder parameter varPROP iatiOSITION: ons
the




p 0 2, p
1,
x > 0, x < 0
followingpropertiesholdtrue:
For all branchesareontheRe- axis
(b)If amultiplepole withmultiplicity then isa zeroof multiplicity
at least ie theroot
(a)
 

( ) ( )s sF,G F,G,bp sz
locushas fixedpoints
(c)If allcancellationsaremadebetween and thenfor thereduced
root locus wecannot have twopolesnext toeachother.

33. Interlacing Properties of RootInterlacing Properties of Root
LocusLocus
• INTERLACING PROPERTY OF ROOT LOCUS
t
sF + G
b,
s(F + xbb )+ G x
:For anRC, or RL network describedby and
with first, or second order parameter variations if
is regular,
then t
(Interlacing
he
Property)THEOREM

followingproperties hold true :
(a) Allpoles and zeros are located on the real axis.
(b) There are no poles and zeros of multiplicity higher than one.
(c) There cannot be two poles, or two zeros nex 

z < 0, p, p < z
x < 0
t to each other
(d) a zero, such that for allpoles
For all allpoles move to tPole Mo hvement : e l

Interlacing Property
x > 0
eft and for all
poles move to right

34. Future ResearchFuture Research
♦ Provide a new dimension to system theory by exploring
the properties of the network representations and
network models
♦ Develop descriptions of system structure evolution
♦ Develop a framework for network redesign, by studying
structure assignment problems
♦ Provide a formal way for describing issues of duality
and analogy
♦ Develop a multi-parameter approach for re-engineering
based on the DAP formulation.

35. APPENDIXAPPENDIX

36. Dimensional Variability ofDimensional Variability of
Interconnection GraphInterconnection Graph
f
t4
t5
e
ba
t6
c
d
t1
t2
t3
t7
, , , , , :a b c d e f SCALARS OF VECTORS WITH DIFFERENT DIMENSIONS
1 2 3 4 5 6 7, , , , , , :t t t t t t t VECTOR SIGNALS (VERTICES) & VECTOR FUNCTIONS
EARLY STAGES: SCALAR SIGNALS (VERTICES) & SCALAR FUNCTIONS (EDGES)
LATE STAGES: VECTOR SIGNALS (VERTICES) & VECTOR FUNCTIONS (EDGES)
PROBLEMS:
 REPRESENTATION OF DIMENSIONAL VARIABILITY
 SYSTEM PROPERTIES AND DIMENSIONAL VARIABILITY
INVARIANCE
EVOLUTION

37. Life Cycle Evolution of Systems:Life Cycle Evolution of Systems:
Growth, DeathGrowth, Death
THEME: GRAPH STRUCTURE EVOLUTION PROBLEMS
t6
t9
t8
t4
g
c
d a
b e
f
t1 t2 t3
t5
t7
PROBLEMS:
GRAPH STRUCTURAL GROWTH PROBLEM
GRAPH LOSS PROBLEM
GRAPH PRESERVATION WITH EDGES REDESIGN
THE REPRESENTATION PROBLEM (DEVELOP AN APPROPRIATE
REPRESENTATION TO DESCRIBE GROWTH, DEATH)

38. Canonical ExampleCanonical Example
1 2
3 +
+
+ + +
-
1w 1e 1y
2w
2e 2y
3y 3e
3w
: , 1, 2, 3
i i i i i
i
i i i
x A x B e
S i
y C x
  
 
 

AGGREGATE SYSTEM:  , ,aS A B C
1 1 1
2 2 2
3 3 3
0 0 0 0 0 0
0 0 , 0 0 , 0 0
0 0 0 0 0 0
A B C
A A B B C C
A B C
     
            
          
INTERCONNECTION RULE:
0 0
, 0
0 0
I
e w F y F I I
I
 
     
  COMPOSITE SYSTEM:    , , , ,c aS A B C S A B C F 
1 1 3
2 1 2 2 3
3 2 3
0
, ,
0
A B C
A A BFC B C A B C B B C C
B C A
 
      
  

39. Composition, Completeness &
Equivalent Feedback Configuration
GIVEN: (i) TOPOLOGY  SYSTEM INTERCONNECTIONS
(ii) FAMILY OF SUBSYSTEM MODELS
COMPOSITION
ASSUMPTIONS:
ke

kG
,k jF
,1 1kF z 
,k j jF z
kw
k
kz
jz
1,2,...,j  : i i iG e z
EQUIVALENT FEEDBACK
CONFIGURATION:
w +
+
e
 G s
F
z
 
 
z G s e
e w Fz
THE COMPLETENESS ASSUMPTION:
(i) SUBSYSTEM OUTPUT ,
(ii) EXOGENOUS SUBSYSTEM INPUTS DEGREES OF FREEDOM :
, 1,2,...,k ky z k  
kw kl
 1dim colsp ;...; , 1,2,...,k k kl F F k    

40. Equivalent Feedback Configuration:
Non-Complete Composite Systems
INTERCONNECTIONS
REMARK: DEVIATIONS FROM COMPLETENESS CORRESPONDS TO INPUT-OUTPUT
DECENTRALISED SQUARING DOWN
REMARK: THE SYSTEM GRAPH BECOMES ESSENTIAL FOR THE STRUCTURAL
PROPERTIES OF NONCOMPLETE SYSTEMS
- AGGREGATE A
INPUT
STRUCTURE
:L OUTPUT
STRUCTURE
:K
u
1L
L0
0


w
1
0
0

z y1K
K
0
0
COMPOSITE SYSTEM ; ; ; :C a L K 

41. Design Time Dependent EvolutionDesign Time Dependent Evolution
In Integrated DesignIn Integrated Design
ASSUMPTION: INTERCONNECTION TOPOLOGY FIXED, SUBPROCESS MODELS
MAY HAVE VARIABLE COMPLEXITY
EARLY
(simple)
LATE
(complex)
EVOLUTION OF
MODELS IN EARLY
DESIGN
 = 0
  1  2  3  …
   0
ISSUES:
 MODELLING IN EARLY – LATE DESIGN:
AN EVOLUTIONARY STRUCTURAL PROCESSES
 VARIABLE DIMENSIONALITY MODELLING
 VARIABLE COMPLEXITY MODELLING
0


1
k




42. Variable Complexity Modelling
ASSUMPTION: FIXED DIMENSIONALITY OF VERTICES, BUT VARIABLE
COMPLEXITY MODELLING FOR SUBSYSTEMS
 = 0
  1  2  3  …    0
KERNEL
MODEL
GRAPH STEADY-
STATE
GRAPH + FIRST
ORDER DYNAMICS
GRAPH + FULL
LINEAR MODELS
GRAPH + NON-
LINEAR MODEL
1 :k k k   1kNESTING: IS A STRUCTURED SIMPLIFICATION OF
PROBLEMS:
STRUCTURED MODEL REDUCTION THAT PRESERVES INTERCONNECTION RULE.
VARIABILITY AND INVARIANCE OF SYSTEM PROPERTIES UNDER STRUCTURED
MODEL REDUCTION.
PREDICTION OF PROPERTIES OF FULL MODEL FROM THE PROPERTIES OF SIMPLE
(EARLY) MODELS.
INVARIANCE EVOLUTION

43. The Notion of Kernel ModelThe Notion of Kernel Model
  : , : :i i i i ii
e w g e wSUBSYSTEMS:
, :i ie w INPUT, OUTPUT VERTICES
:ig INPUT - OUTPUT OPERATOR
 1,2,...., :a i
i    AGGREGATE SYSTEM
   1 2 1 2, ,..., , , ,...,e e e w w w   
KERNEL GRAPH: A RELATION :C    i.e. A SUBSET OF  
KERNEL FUNCTION:
 
 
, ,
: :
, ,
if
if
j k C
C jk j k jk
j k C
w e
f w e f
w e
     
   
    





KERNEL MODEL OF COMPOSITE SYSTEM:
 
1
* :C
C k jk ja a
j
e f w


 
   
 
   