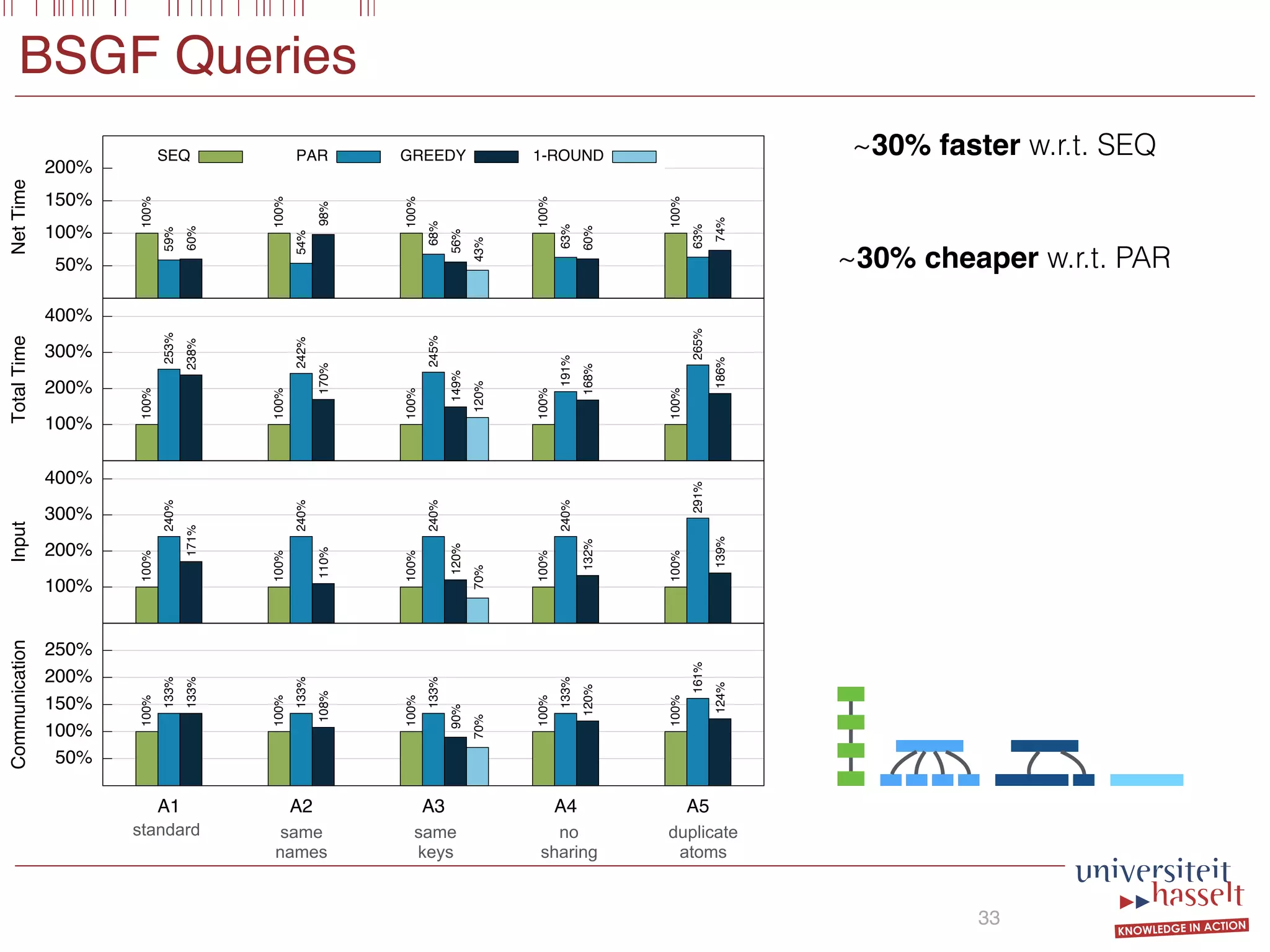
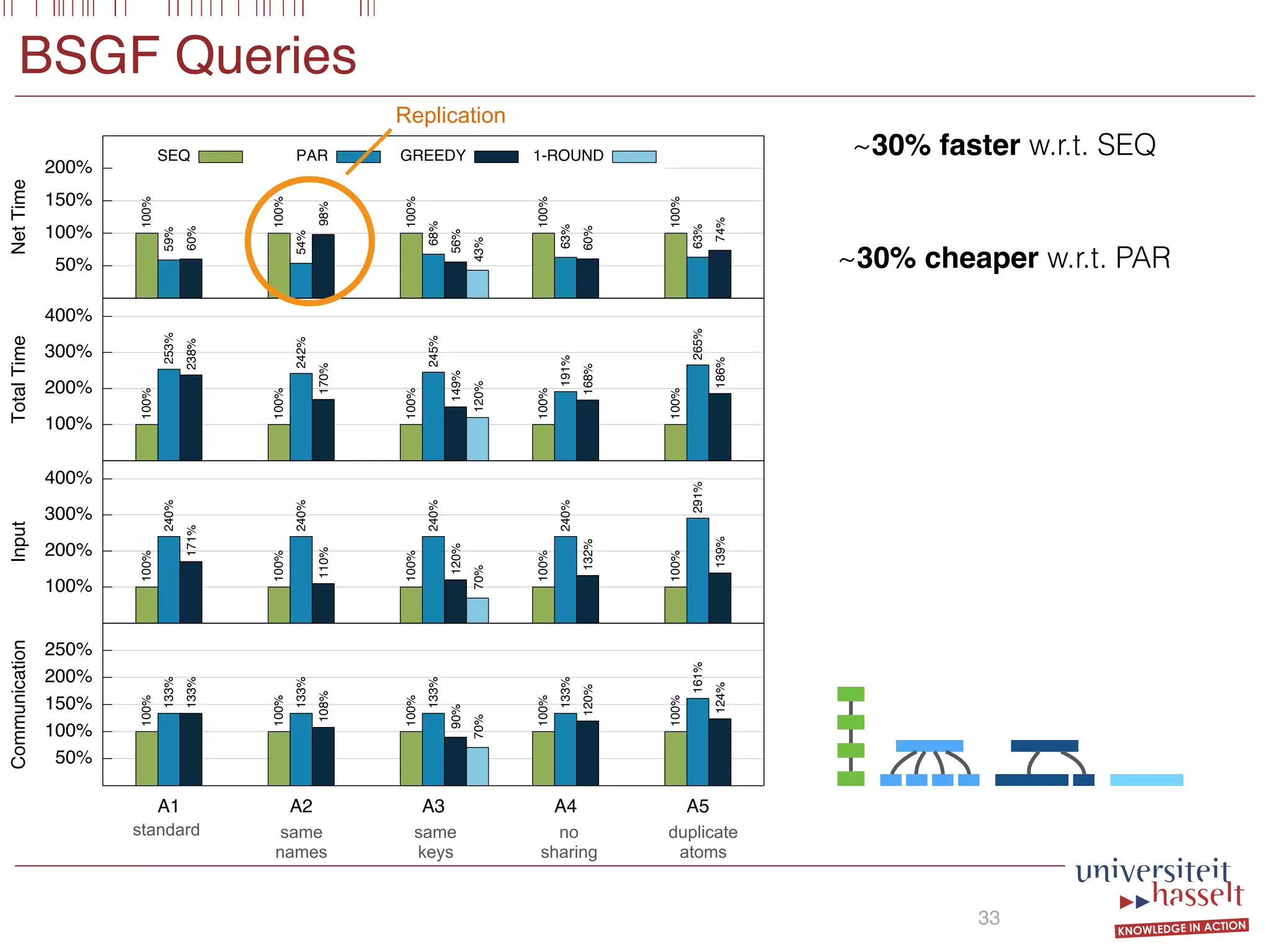
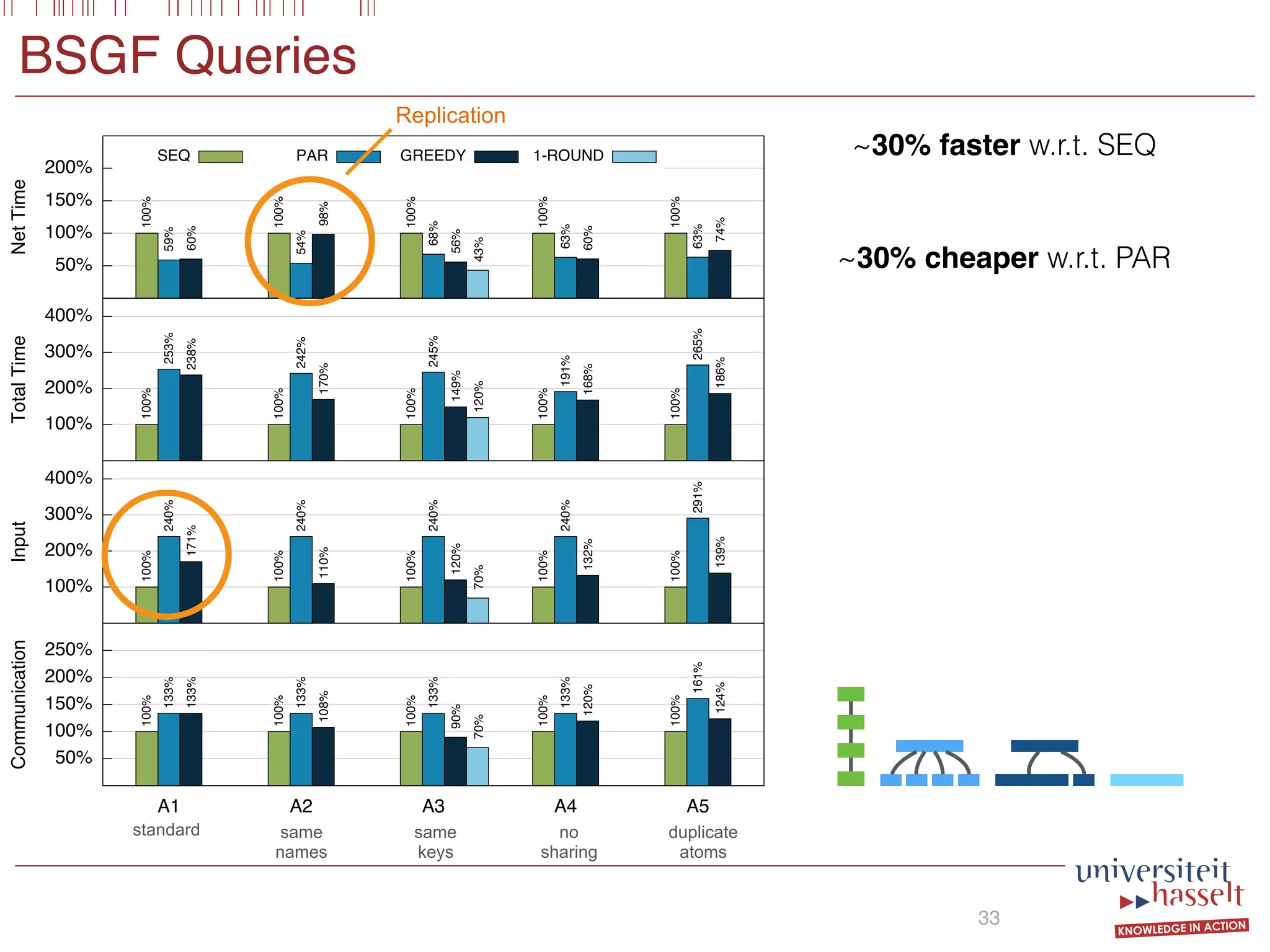
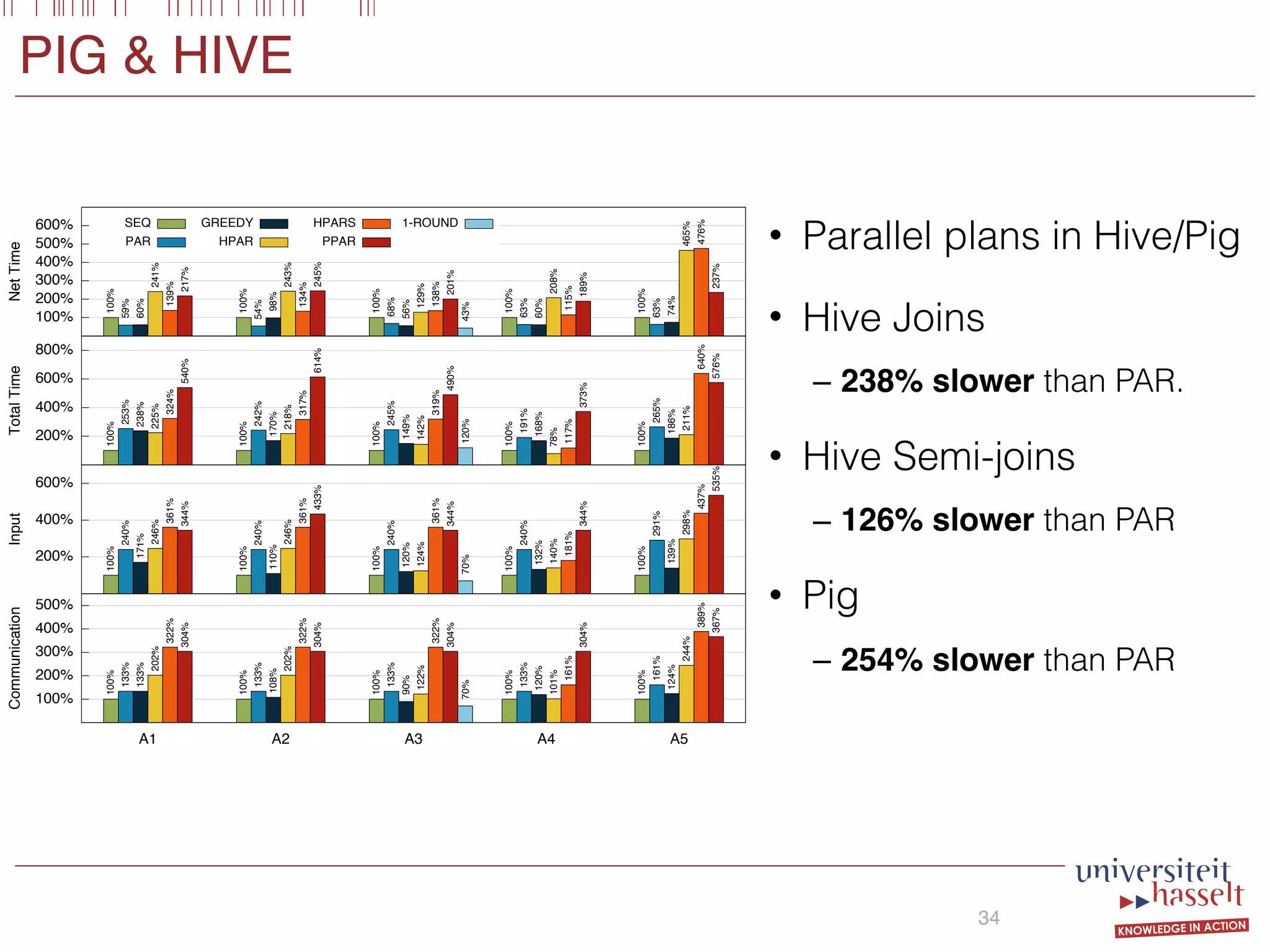
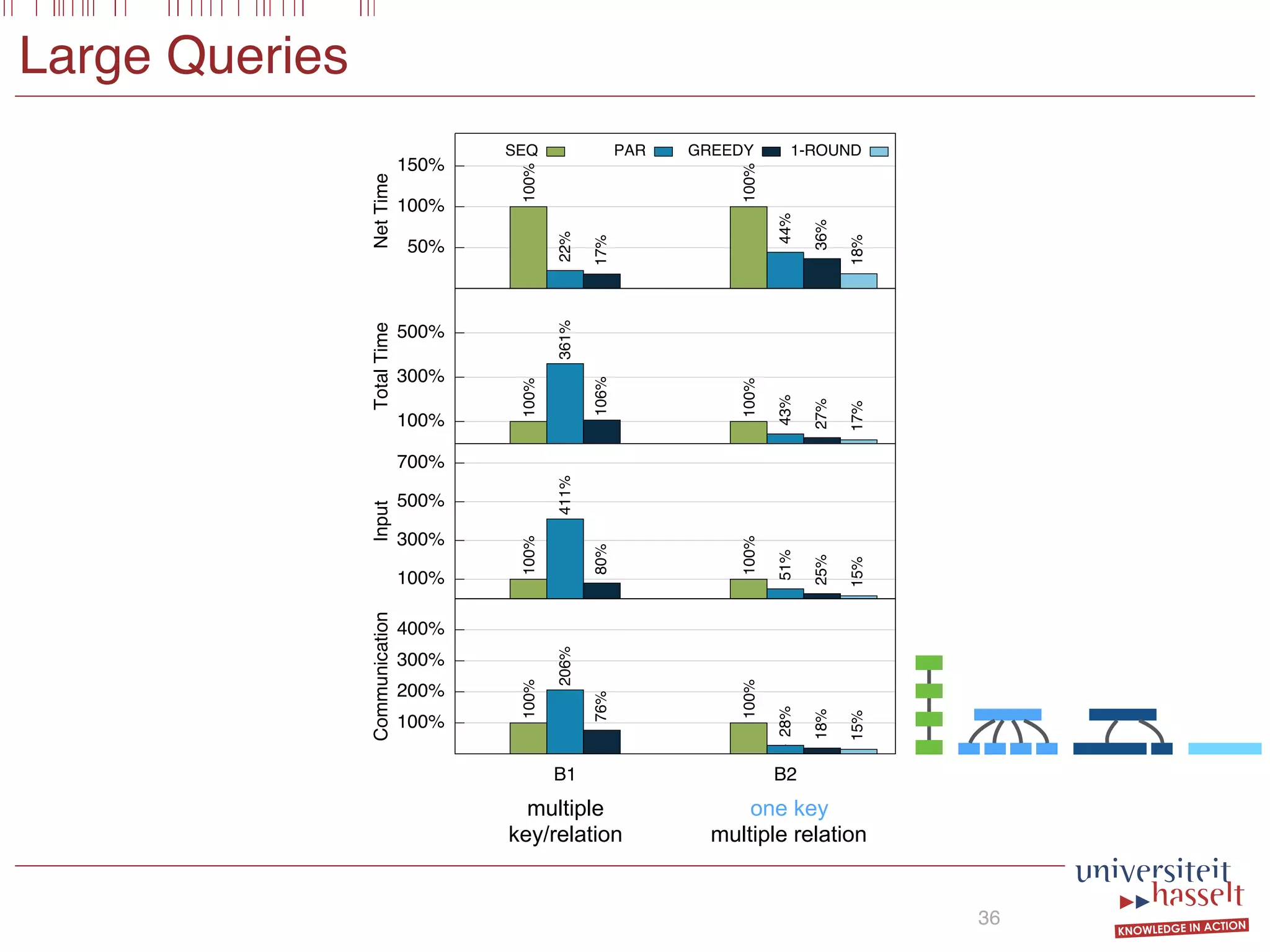
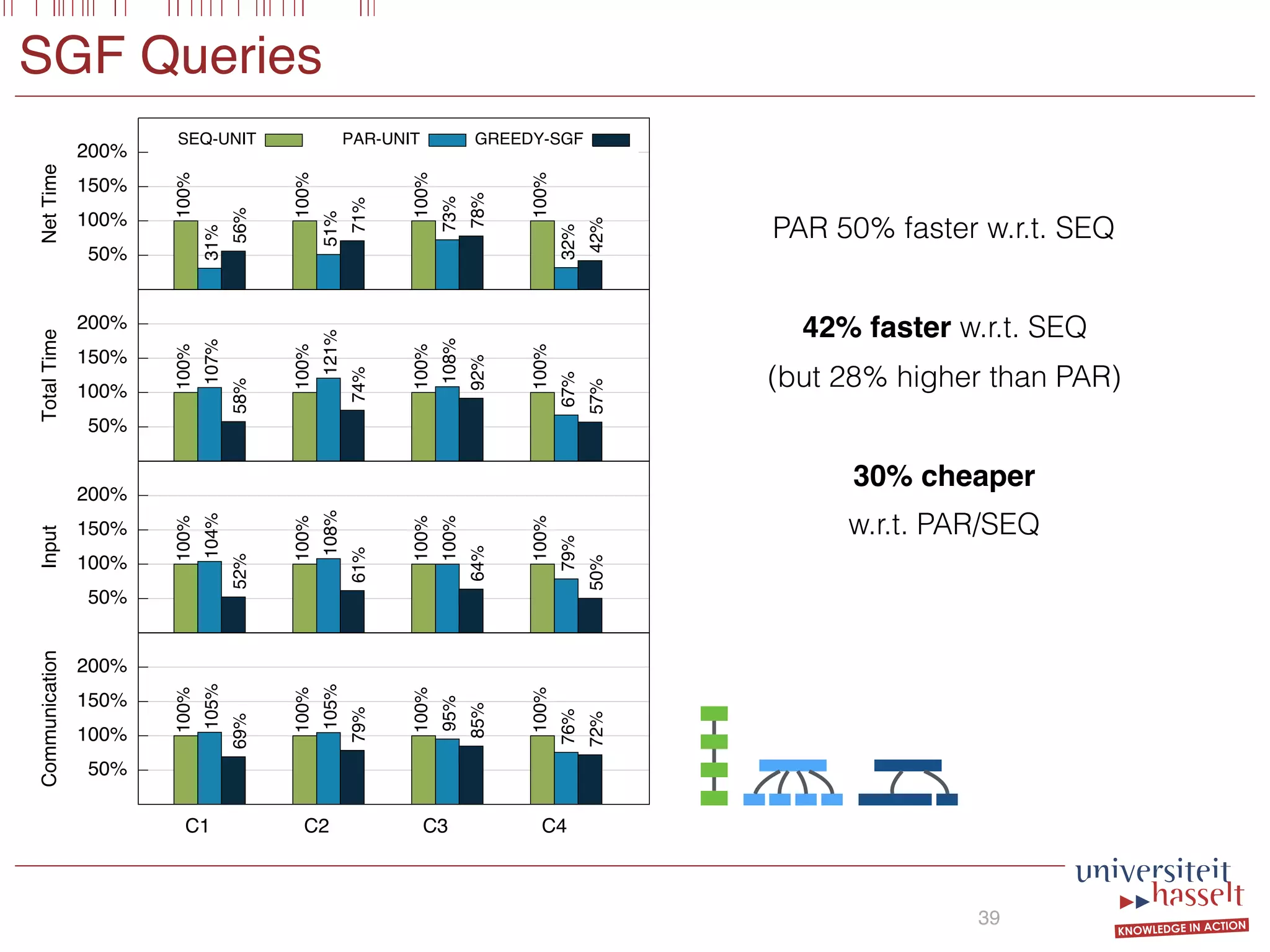
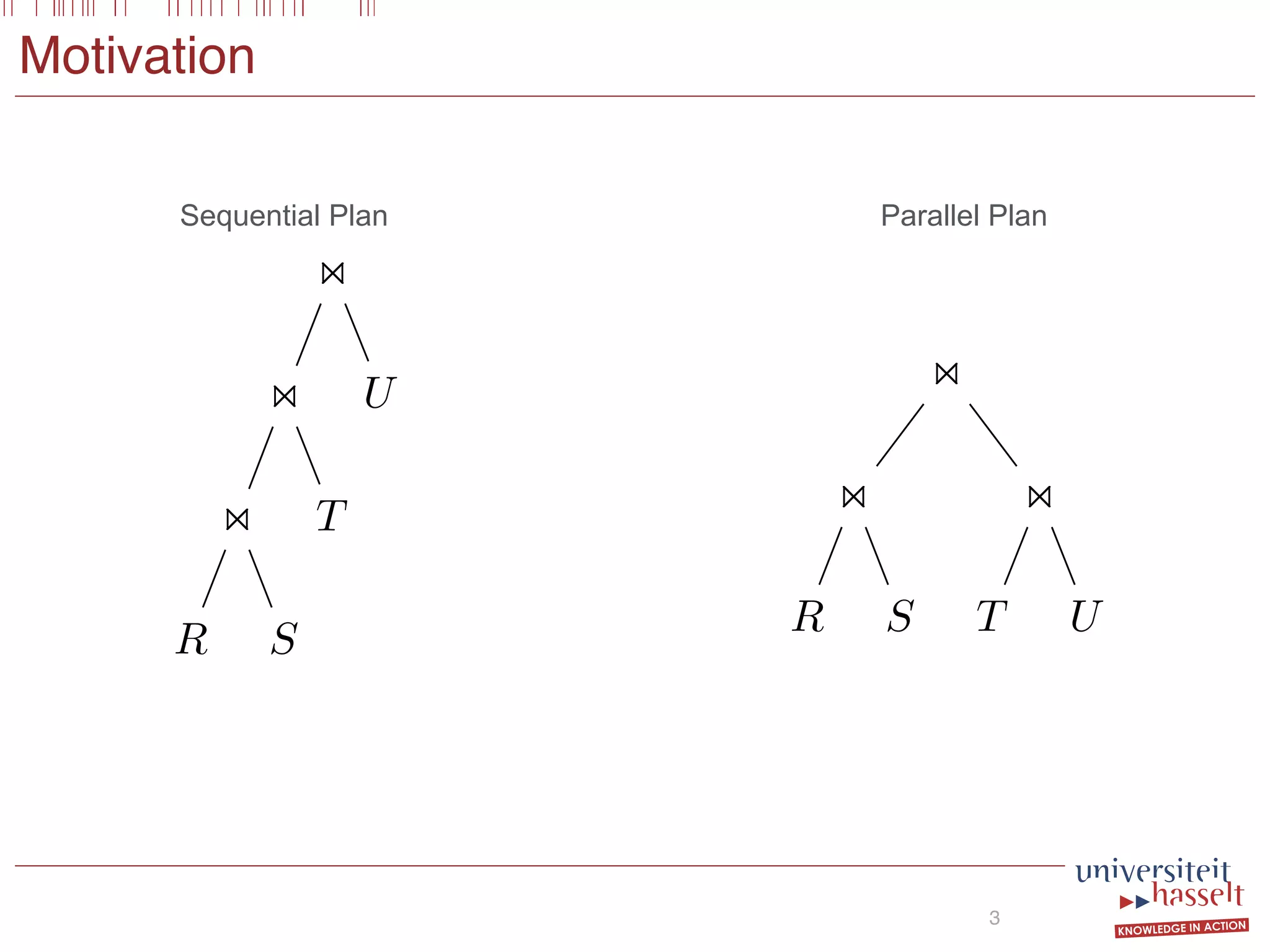
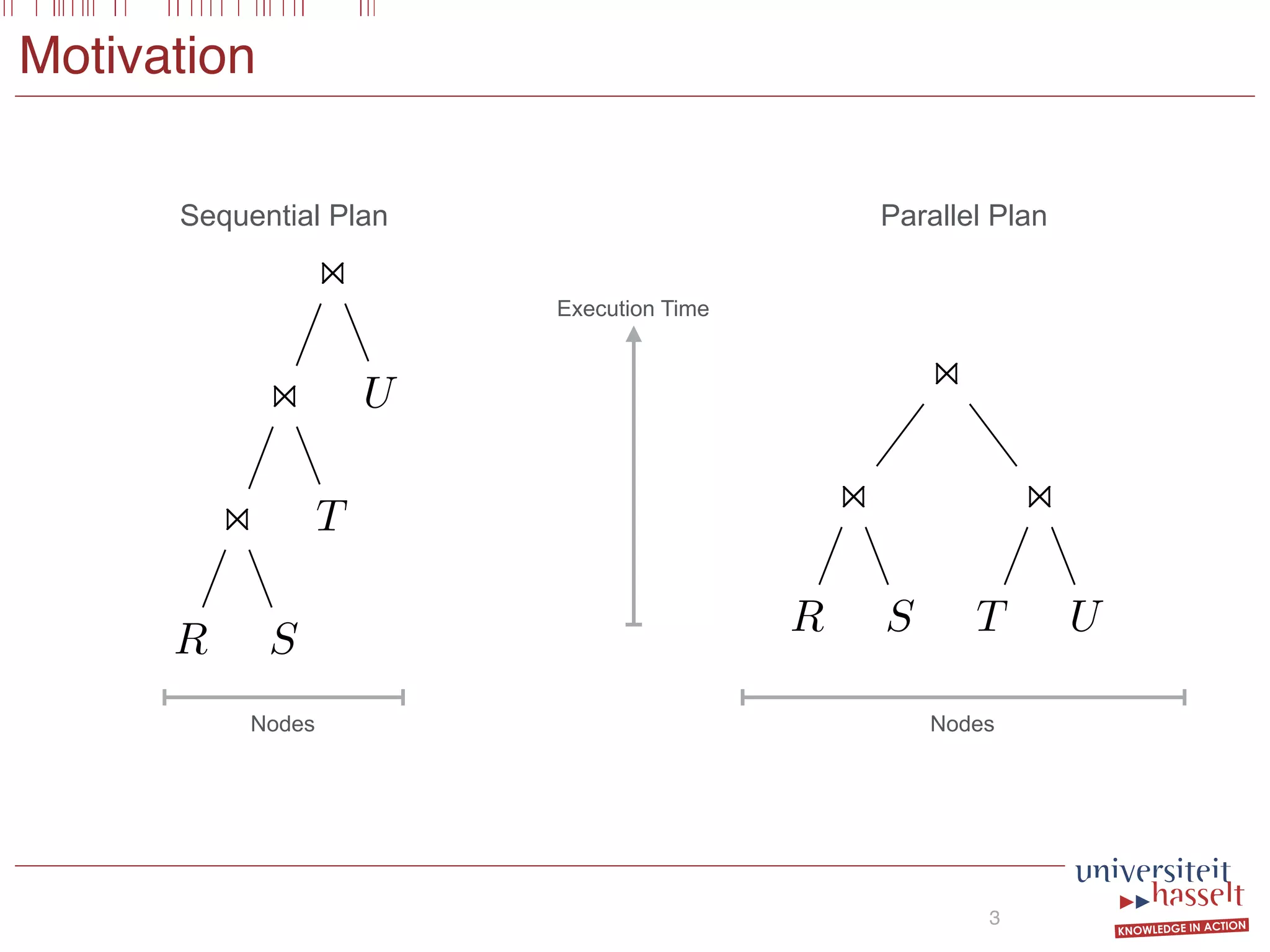
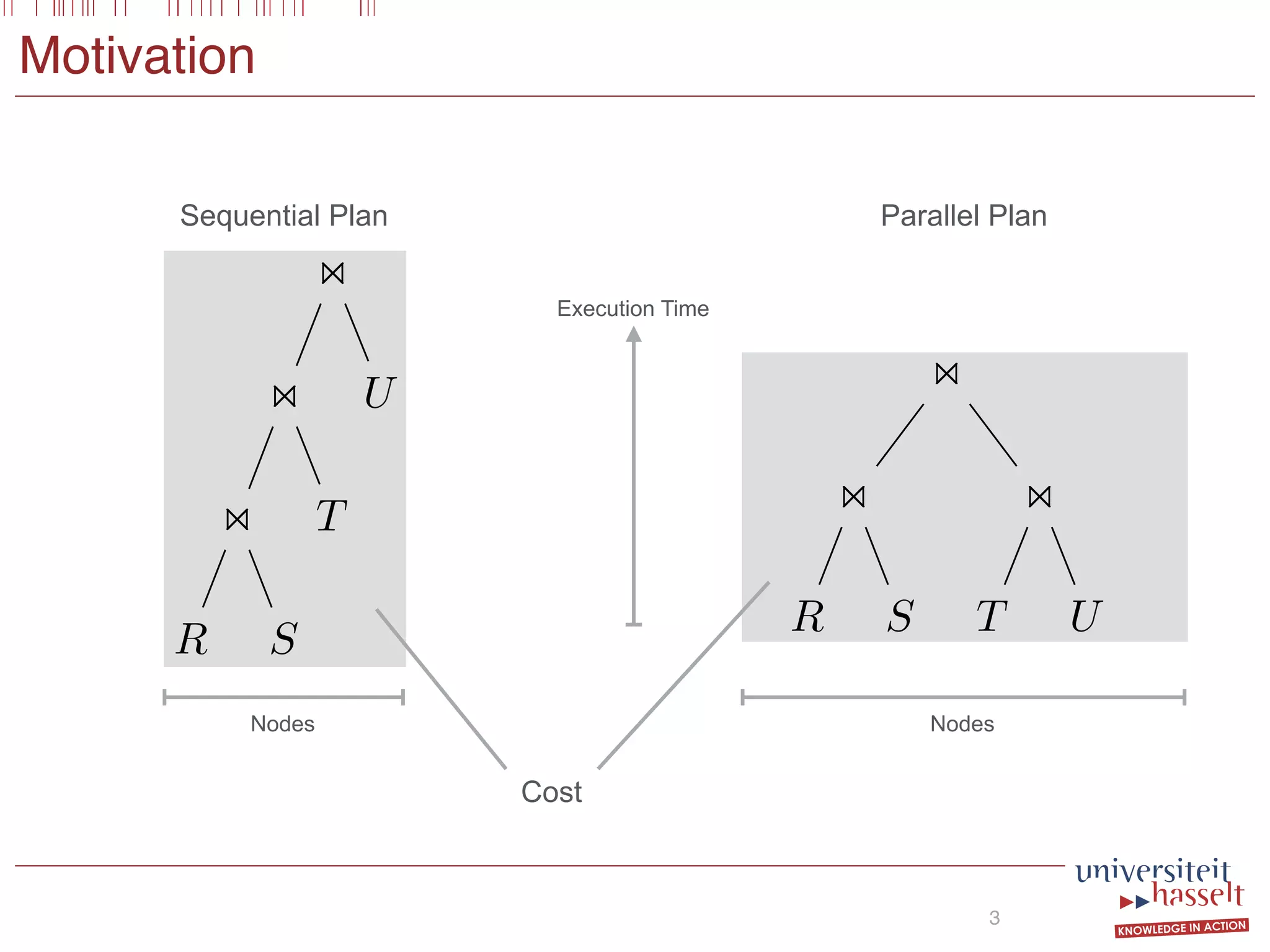
This document discusses the parallel evaluation of multi-semi-joins, highlighting techniques utilizing MapReduce to optimize query execution time and cost through a strictly guarded fragment (SGF) query language. It demonstrates the evaluation process for semi-joins, multi-semi-joins, and provides a cost model for the MapReduce framework. The document also emphasizes the importance of separating different inputs during the map phase to ensure accurate cost calculation and presents experimental results to validate the proposed adjustments.

1. Parallel Evaluation of Multi-Semi-Joins
Jonny Daenen | Hasselt University
Jonny Daenen | Hasselt University
Frank Neven | Hasselt University
Tony Tan | National Taiwan University
Stijn Vansummeren | Université Libre de Bruxelles

2. Main Contribution
• Parallel evaluation (MapReduce)
• Strictly Guarded Fragment
• 2-round eval: low net time (elapsed)
• 2-tier optimization: total time (cost)
2

3. Motivation
3
on
on
on
R S
T
U
on
on
R S
on
T U
Sequential Plan Parallel Plan

4. Motivation
3
on
on
on
R S
T
U
on
on
R S
on
T U
Execution Time
Nodes Nodes
Sequential Plan Parallel Plan

5. Motivation
3
on
on
on
R S
T
U
on
on
R S
on
T U
Execution Time
Nodes Nodes
Sequential Plan Parallel Plan
Cost

6. Overview
• SGF Query Language
• Evaluation
– Semi-joins
– Multi-Semi-Joins
– BSGF
– SGF
• Experiments
• Conclusion
4

7. Query Language
Strictly Guarded Fragment

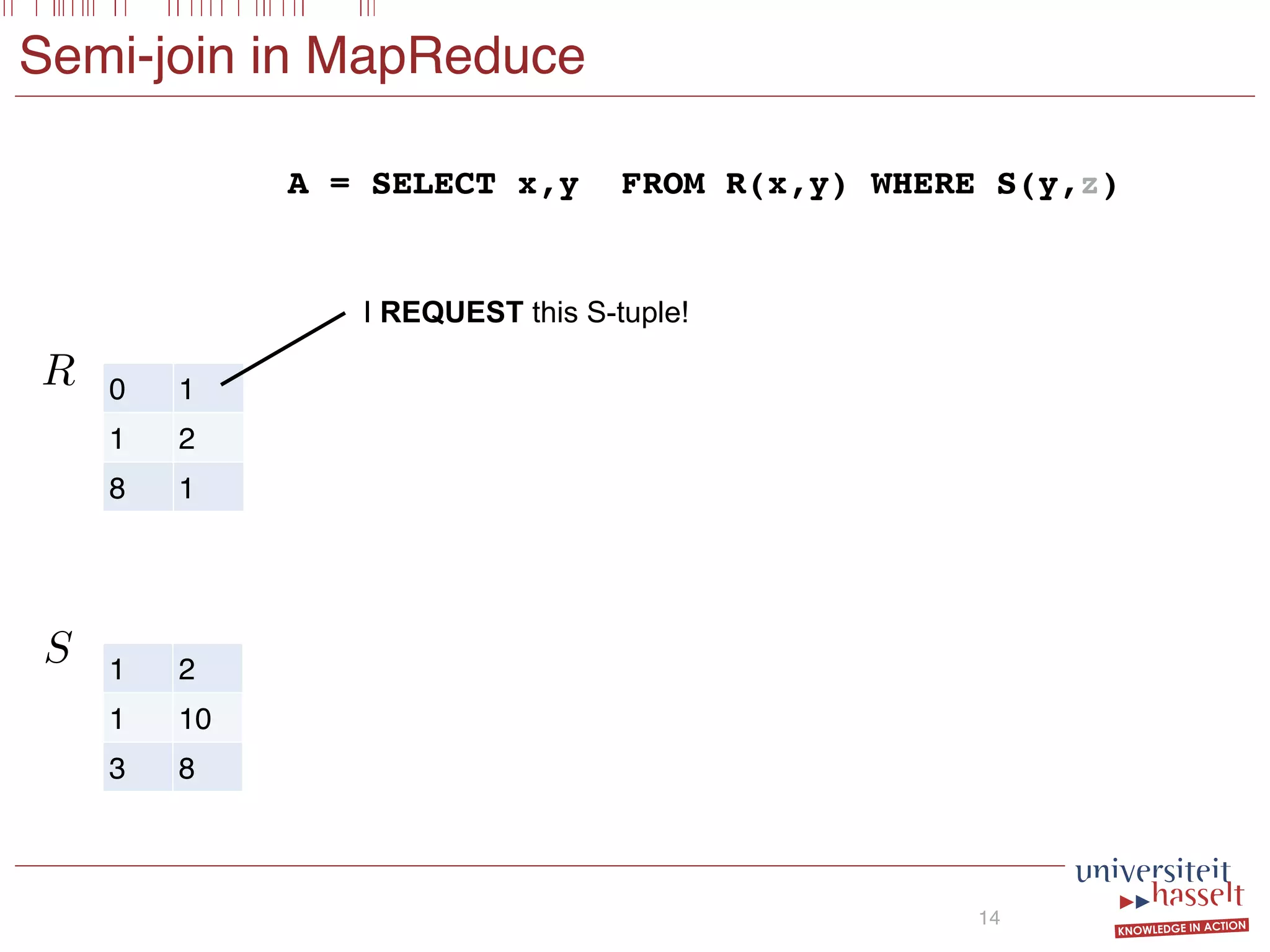
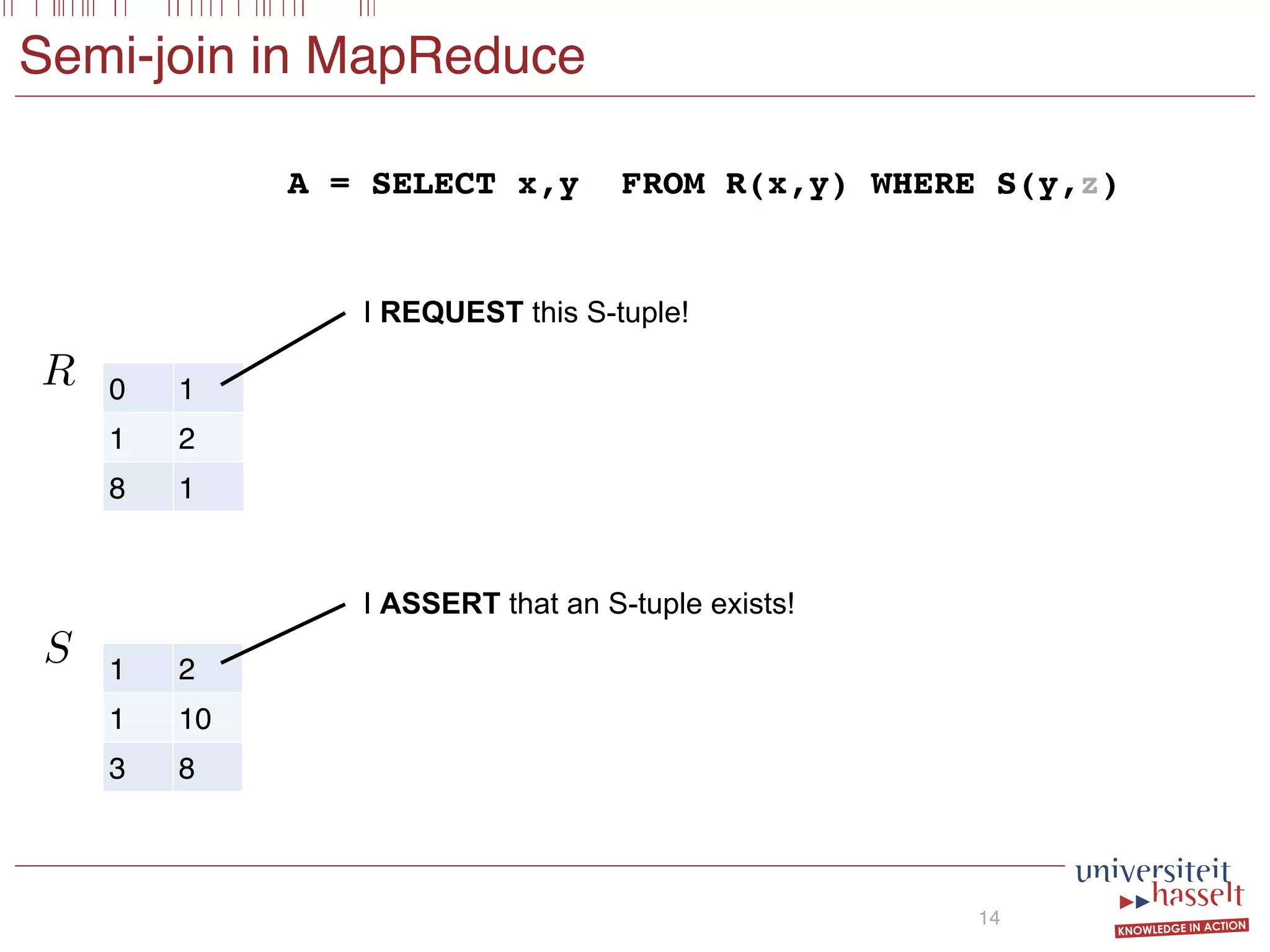
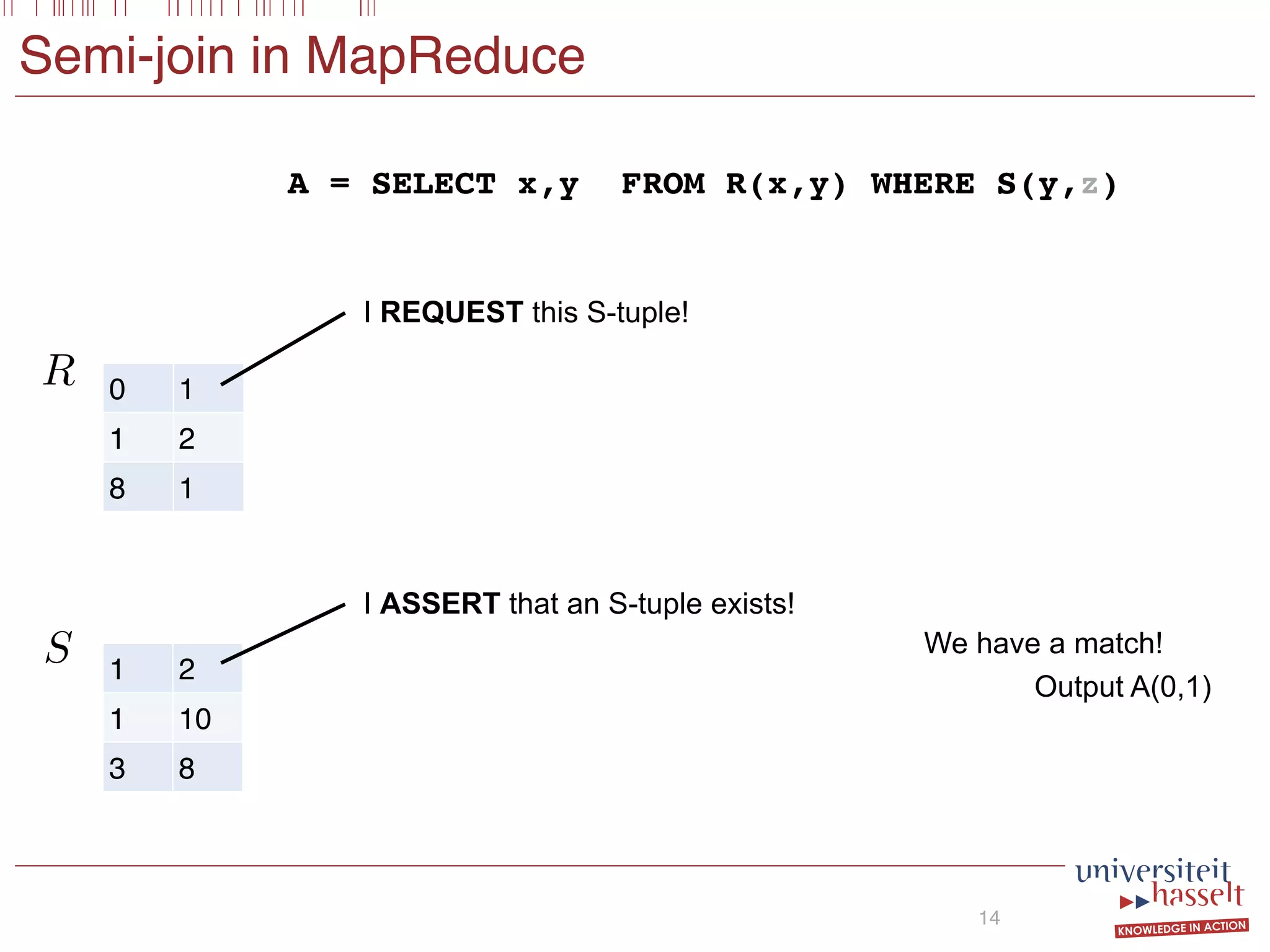
8. SELECT x
FROM R(x,y)
WHERE
[S(x,y) AND T(x)] OR NOT U(y,x)
SGF Query
6
1 Guard Atom
Conditional Atoms
Boolean Combination
(x,y) IN S
• Basic (BSGF): no nesting
• Semi-join algebra

9. Example
7
pository, respectively. Let Upcoming contain tuples (new-
title, author) of upcoming books. The following query se-
lects all the upcoming books (newtitle, author) of authors
that have not yet received a “bad” rating for the same title
at all three book retailers; Z2 is the output relation:
Z1 := SELECT aut FROM Amaz(ttl, aut, ”bad”)
WHERE BN(ttl, aut, ”bad”) AND BD(ttl, aut, ”bad”);
Z2 := SELECT (new, aut) FROM Upcoming(new, aut)
WHERE NOT Z1(aut);
Note that this query cannot be written as a basic SGF query,
since the atoms in the query computing Z1 must share the
ttl variable, which is not present in the guard of the query
computing Z2. ✷
a given
analyzi
one int
The ad
below,
differen
data.
Whi
and red
ure 1 s
See [37
phase
(ii) sor
by the
disk.
Example 2. Let Amaz, BN, and BD be relations con-
taining tuples (title, author, rating) corresponding to the
books found at Amazon, Barnes and Noble, and Book De-
pository, respectively. Let Upcoming contain tuples (new-
title, author) of upcoming books. The following query se-
lects all the upcoming books (newtitle, author) of authors
that have not yet received a “bad” rating for the same title
at all three book retailers; Z2 is the output relation:
Z1 := SELECT aut FROM Amaz(ttl, aut, ”bad”)
WHERE BN(ttl, aut, ”bad”) AND BD(ttl, aut, ”bad”);
Z2 := SELECT (new, aut) FROM Upcoming(new, aut)
WHERE NOT Z1(aut);
Note that this query cannot be written as a basic SGF query,
since the atoms in the query computing Z1 must share the
ttl variable, which is not present in the guard of the query
computing Z2. ✷
3.3
As o
plans,
a given
analyz
one int
The ad
below,
differen
data.
Whi
and red
ure 1 s
See [37
phase
(ii) sor
by the
disk.

10. MapReduce
in Hadoop

11. MapReduce (in Hadoop)
• Map creates Key-value pairs
• Reducer combines values
• Cost Model (Wang et al., 2013)
9
Map
Shuffle
Reduce
1 2 3 4
1 2 3 4
1 2 3 4
1 2 3 4
Input
Map
Output
Reduce
Input
Reduce
Output

12. MapReduce (in Hadoop)
• Map creates Key-value pairs
• Reducer combines values
• Cost Model (Wang et al., 2013)
9
Map
Shuffle
Reduce
1 2 3 4
1 2 3 4
1 2 3 4
1 2 3 4
Input
Map
Output
Reduce
Input
Reduce
Output
Let I1 ∪ · · · ∪ Ik denote the partition of the input tuples
such that the mapper behaves uniformly1
on every data item
in Ii. Let Ni be the size (in MB) of Ii, and let Mi be the
size (in MB) of the intermediate data output by the mapper
on Ii. The cost of the map phase on Ii is:
costmap(Ni, Mi) = hrNi + mergemap(Mi) + lwMi,
where mergemap(Mi), denoting the cost of sort and merge in
the map stage, is expressed by
mergemap(Mi) = (lr + lw)Mi logD
(Mi+Mi)/mi
buf map
.
See Table 1 for the meaning of the variables hr, lw, lr, lw,
D, Mi, mi, and buf map.2
The total cost incurred in the map
phase equals the sum
k
i=1
costmap(Ni, Mi). (2)
Let I1 ∪ · · · ∪ Ik denote the partition of the input tuples
such that the mapper behaves uniformly1
on every data item
in Ii. Let Ni be the size (in MB) of Ii, and let Mi be the
size (in MB) of the intermediate data output by the mapper
on Ii. The cost of the map phase on Ii is:
costmap(Ni, Mi) = hrNi + mergemap(Mi) + lwMi,
where mergemap(Mi), denoting the cost of sort and merge in
the map stage, is expressed by
mergemap(Mi) = (lr + lw)Mi logD
(Mi+Mi)/mi
buf map
.
See Table 1 for the meaning of the variables hr, lw, lr, lw,
D, Mi, mi, and buf map.2
The total cost incurred in the map
phase equals the sum
k
i=1
costmap(Ni, Mi). (2)
Note that the cost model in [27, 36] defines the total cost
incurred in the map phase as
costmap
k
i=1
Ni,
k
i=1
Mi . (3)
The latter is not always accurate. Indeed, consider for in-
stance an MR job whose input consists of two relations R
and S where the map function outputs many key-value pairs
for each tuple in R and at most one key-value pair for each
tuple in S, e.g., because of filtering. This difference in map
output may lead to a non-proportional contribution of both
input relations to the total cost. Hence, as shown by Equa-
tion (2), we opt to consider different inputs separately. This
cannot be captured by map cost calculation of Equation (3),
as it considers the global average map output size in the cal-
culation of the merge cost. In Section 5, we illustrate this
problem by means of an experiment that confirms the effec-
tiveness of the proposed adjustment.
To analyze the cost in the reduce phase, let M = k
i=1 Mi.
The reduce stage involves (i) transferring the intermediate
data (i.e., the output of the map function) to the correct
reducer, (ii) merging the key-value pairs locally for each re-
ducer, (iii) applying the reduce function, and (iv) writing
the output to hdfs. Its cost will be
costred(M, K) = tM + mergered(M) + hwK,
where K is the size of the output of the reduce function (in
MB). The cost of merging equals
mergered(M) = (lr + lw)M logD
M/r
buf red
.
The total cost of an MR job equals the sum
costh +
k
costmap(Ni, Mi) + costred(M, K),
i=1 i=1
The latter is not always accurate. Indeed, consider for in-
stance an MR job whose input consists of two relations R
and S where the map function outputs many key-value pairs
for each tuple in R and at most one key-value pair for each
tuple in S, e.g., because of filtering. This difference in map
output may lead to a non-proportional contribution of both
input relations to the total cost. Hence, as shown by Equa-
tion (2), we opt to consider different inputs separately. This
cannot be captured by map cost calculation of Equation (3),
as it considers the global average map output size in the cal-
culation of the merge cost. In Section 5, we illustrate this
problem by means of an experiment that confirms the effec-
tiveness of the proposed adjustment.
To analyze the cost in the reduce phase, let M = k
i=1 Mi.
The reduce stage involves (i) transferring the intermediate
data (i.e., the output of the map function) to the correct
reducer, (ii) merging the key-value pairs locally for each re-
ducer, (iii) applying the reduce function, and (iv) writing
the output to hdfs. Its cost will be
costred(M, K) = tM + mergered(M) + hwK,
where K is the size of the output of the reduce function (in
MB). The cost of merging equals
mergered(M) = (lr + lw)M logD
M/r
buf red
.
The total cost of an MR job equals the sum
costh +
k
i=1
costmap(Ni, Mi) + costred(M, K),
where costh is the overhead cost of starting an MR job.
1 2 3
the atoms occurring in C are called the
We interpret Z as the output relation of
DB, the BSGF query (1) defines a new
ing all tuples ¯a for which there is a substi-
ariables occurring in ¯t such that σ(¯x) = ¯a,
d C evaluates to true in DB under substi-
he evaluation of C in DB under σ is de-
on the structure of C. If C is C1 OR C2,
T C1, the semantics is the usual boolean
C is an atom T(¯v) then C evaluates to
) T(¯v), i.e., if there exists a T-atom in
(σ(¯t)) on those positions where R(¯t) and
es.
e intersection Z1 := R ∩ S and the dif-
− S between two relations R and S are
ws:
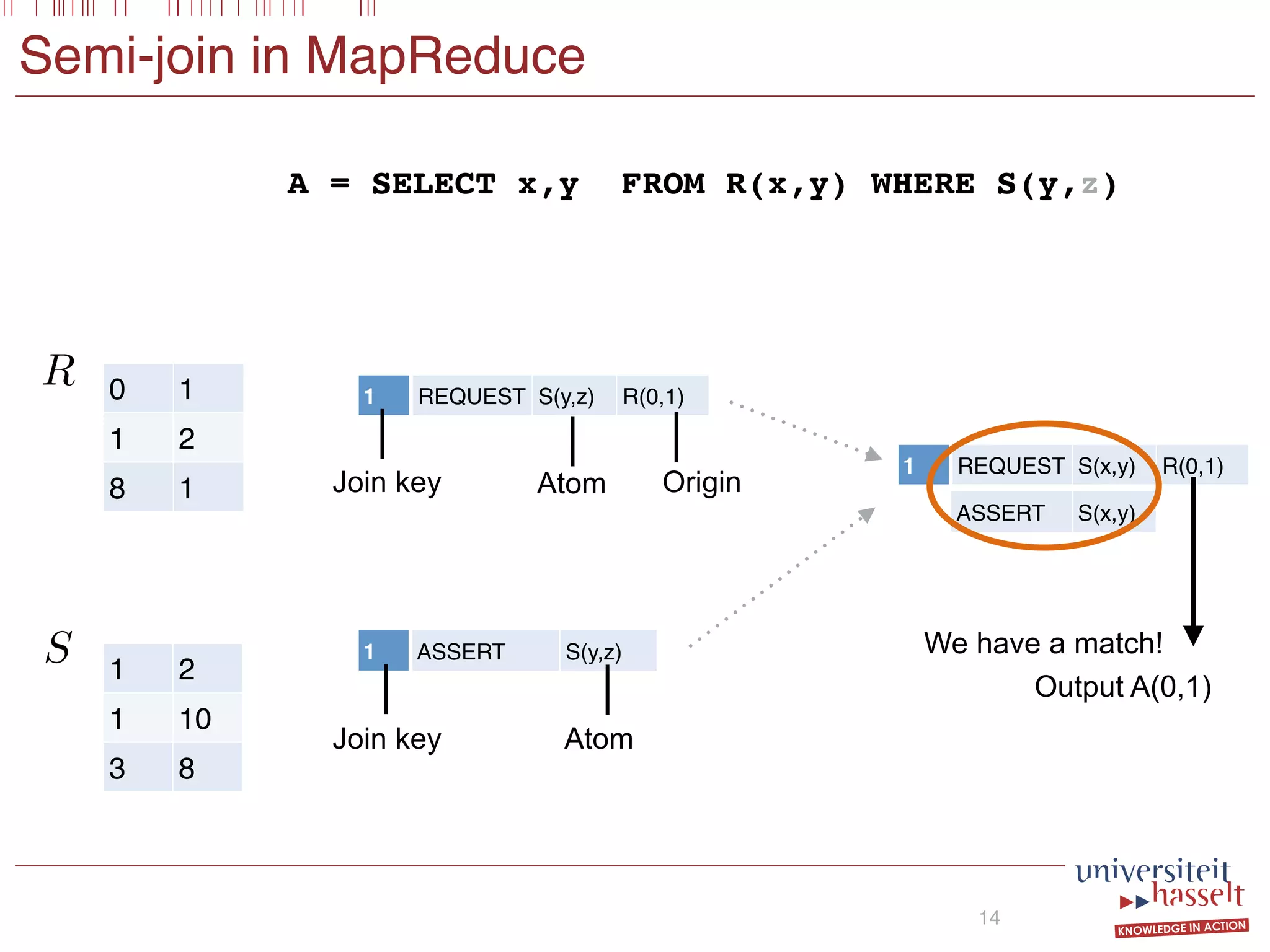
LECT ¯x FROM R(¯x) WHERE S(¯x);
LECT ¯x FROM R(¯x) WHERE NOT S(¯x);
Input Intermediate Data Output
Map Phase
read → map → sort → merge →
Reduce Phase
trans. → merge → reduce → write
Figure 1: A depiction of the inner workings of Hadoop MR.
Remark 1. The syntax we use here differs from the tra-
ditional syntax of the Guarded Fragment [20], and is ac-
tually closer in spirit to join trees for acyclic conjunctive
queries [9, 11], although we do allow disjunction and nega-
tion in the where clause. In the traditional syntax, a pro-
jection in the guarded fragment is only allowed in the form
∃ ¯wR(¯x)∧ϕ(¯z) where all variables in ¯z must occur in ¯x. One
can obtain a query in the traditional syntax of the guarded
fragment from our syntax by adding extra projections for
the atoms in C. For example,
SELECT x FROM R(x, y) WHERE S(x, z1) AND NOT S(y, z2)
632 4 51
4
5
5
2

13. Query Evaluation
In MapReduce

14. Single Semi-Join
Evaluation

15. Semi-Join
12
R n S = ⇡R.⇤(R on S)
R.A R.B
0 1
1 2
8 1
S.B S.C
1 2
1 10
3 8
R.A B S.C
0 1 2
0 1 10
8 1 2
8 1 0
R on S
R
S

16. Semi-Join
13
R n S = ⇡R.⇤(R on S)
R.A R.B
0 1
1 2
8 1
S.B S.C
1 2
1 10
3 8
R.A B S.C
0 1 2
0 1 10
8 1 2
8 1 0
R on S
R
S

17. Semi-join in MapReduce
14
0 1
1 2
8 1
1 2
1 10
3 8
R
S
A = SELECT x,y FROM R(x,y) WHERE S(y,z)

18. Semi-join in MapReduce
14
0 1
1 2
8 1
1 2
1 10
3 8
R
S
I REQUEST this S-tuple!
A = SELECT x,y FROM R(x,y) WHERE S(y,z)

19. Semi-join in MapReduce
14
0 1
1 2
8 1
1 2
1 10
3 8
R
S
I REQUEST this S-tuple!
I ASSERT that an S-tuple exists!
A = SELECT x,y FROM R(x,y) WHERE S(y,z)

20. Semi-join in MapReduce
14
0 1
1 2
8 1
1 2
1 10
3 8
R
S
I REQUEST this S-tuple!
I ASSERT that an S-tuple exists!
We have a match!
Output A(0,1)
A = SELECT x,y FROM R(x,y) WHERE S(y,z)

21. Semi-join in MapReduce
14
0 1
1 2
8 1
1 2
1 10
3 8
R
S We have a match!
Output A(0,1)
A = SELECT x,y FROM R(x,y) WHERE S(y,z)

22. Semi-join in MapReduce
14
0 1
1 2
8 1
1 2
1 10
3 8
R
S 1 ASSERT S(y,z)
Join key Atom
1 REQUEST S(y,z) R(0,1)
Join key Atom Origin
We have a match!
Output A(0,1)
1 REQUEST S(x,y) R(0,1)
ASSERT S(x,y)
A = SELECT x,y FROM R(x,y) WHERE S(y,z)

23. Multi-Semi-Join
Evaluation
n·

24. Multi-Semi-Join Queries
16
0 1
1 2
8 1
1 2
1 10
3 8
R
S
1 REQUEST S(y,z) R(0,1)
1 ASSERT S(x,y)
1 REQUEST S(x,y) R(0,1)
ASSERT S(x,y)
Output A(0,1)
A = SELECT x,y FROM R(x,y) WHERE S(y,z)
B = SELECT x,y FROM R(x,y) WHERE T(x)
0 REQUEST T(x) R(0,1)
1 REQUEST T(x) R(1,2)
2 REQUEST S(y,z) R(1,2)
1
7
3
1 ASSERT T(x)
REQUEST T(x) R(1,2)
ASSERT T(x)
Output B(1,2)
T

25. BSGF Queries
Evaluation & Optimization

26. SELECT x,y FROM R(x,y)
WHERE [S(x,y) OR S(y,x)] AND T(x,z)
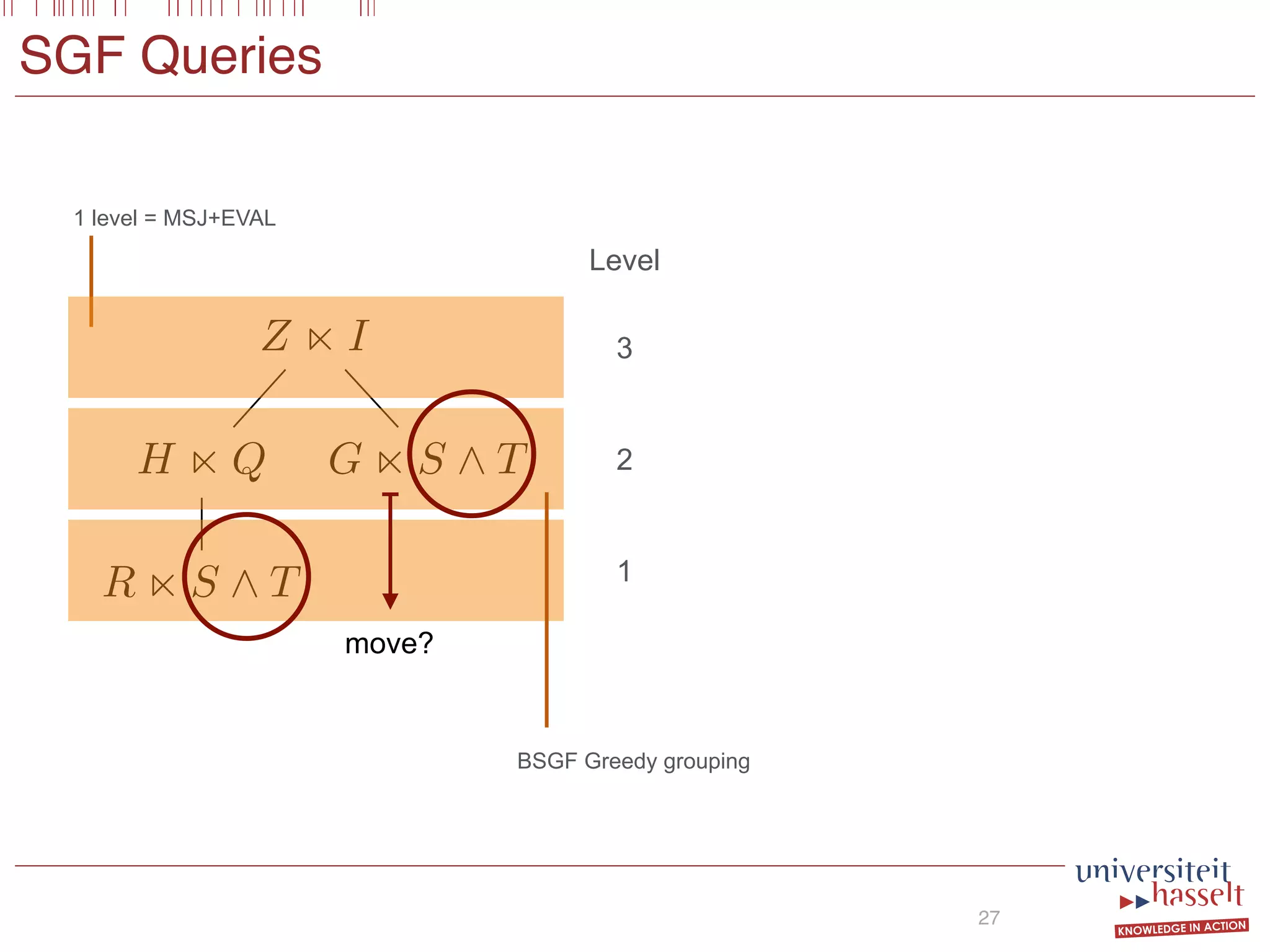
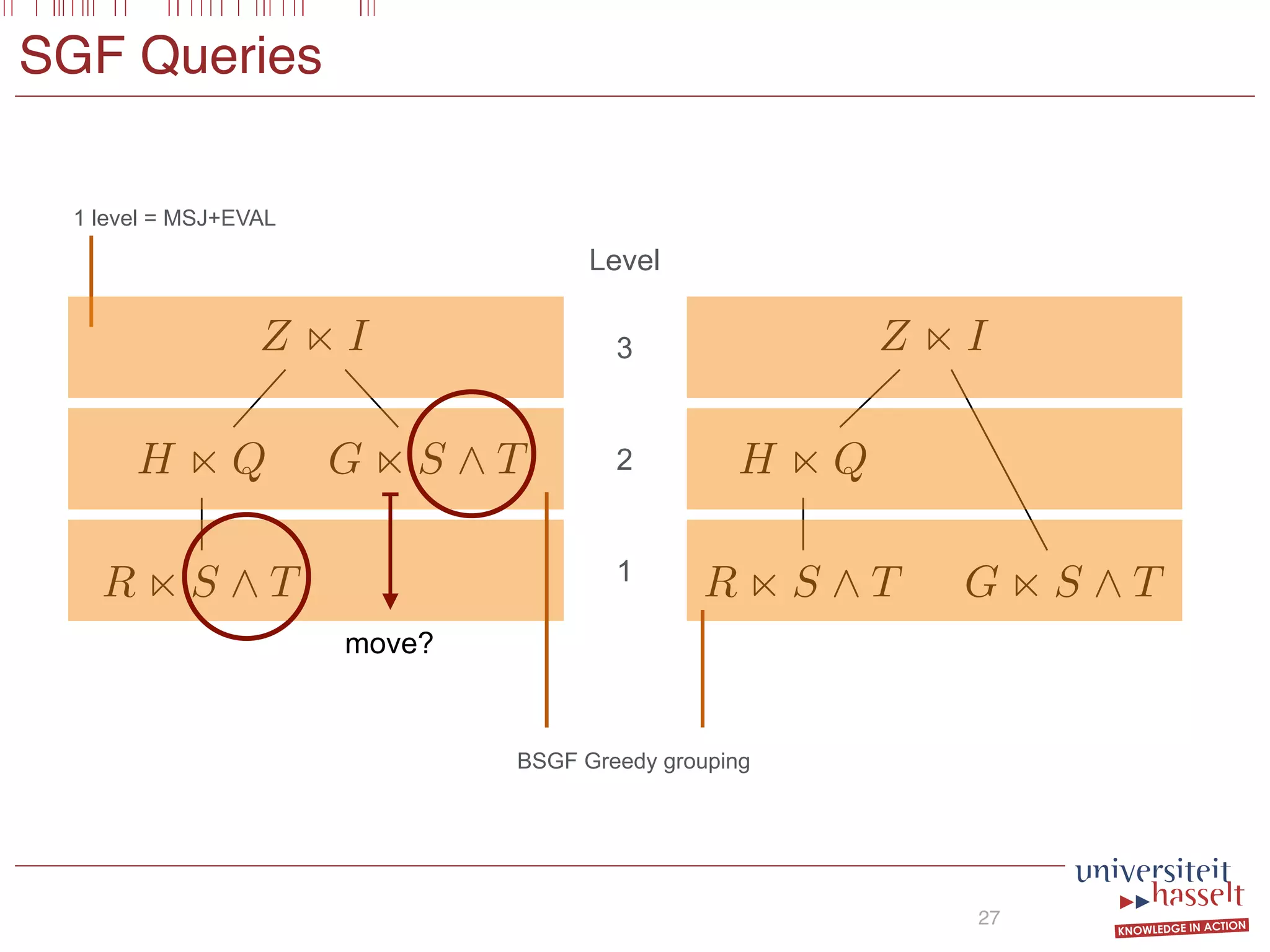
BSGF Queries
18
massively
g., [2–5, 7,
d in terms
me, amount
he number
m to bring
query end
important
no longer
ces such as
the cost is
Attribution-
view a copy
-nd/4.0/. For
n by emailing
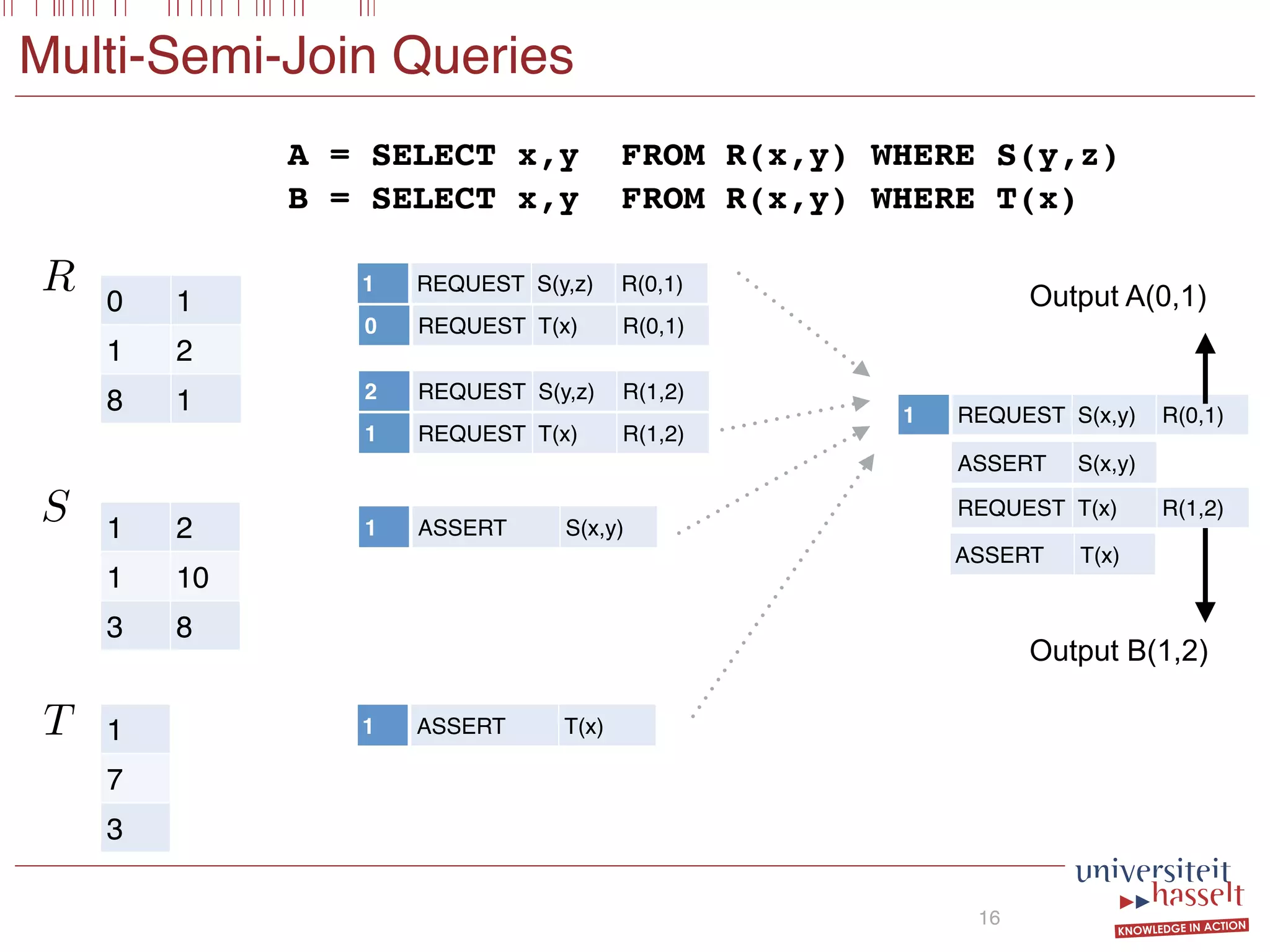
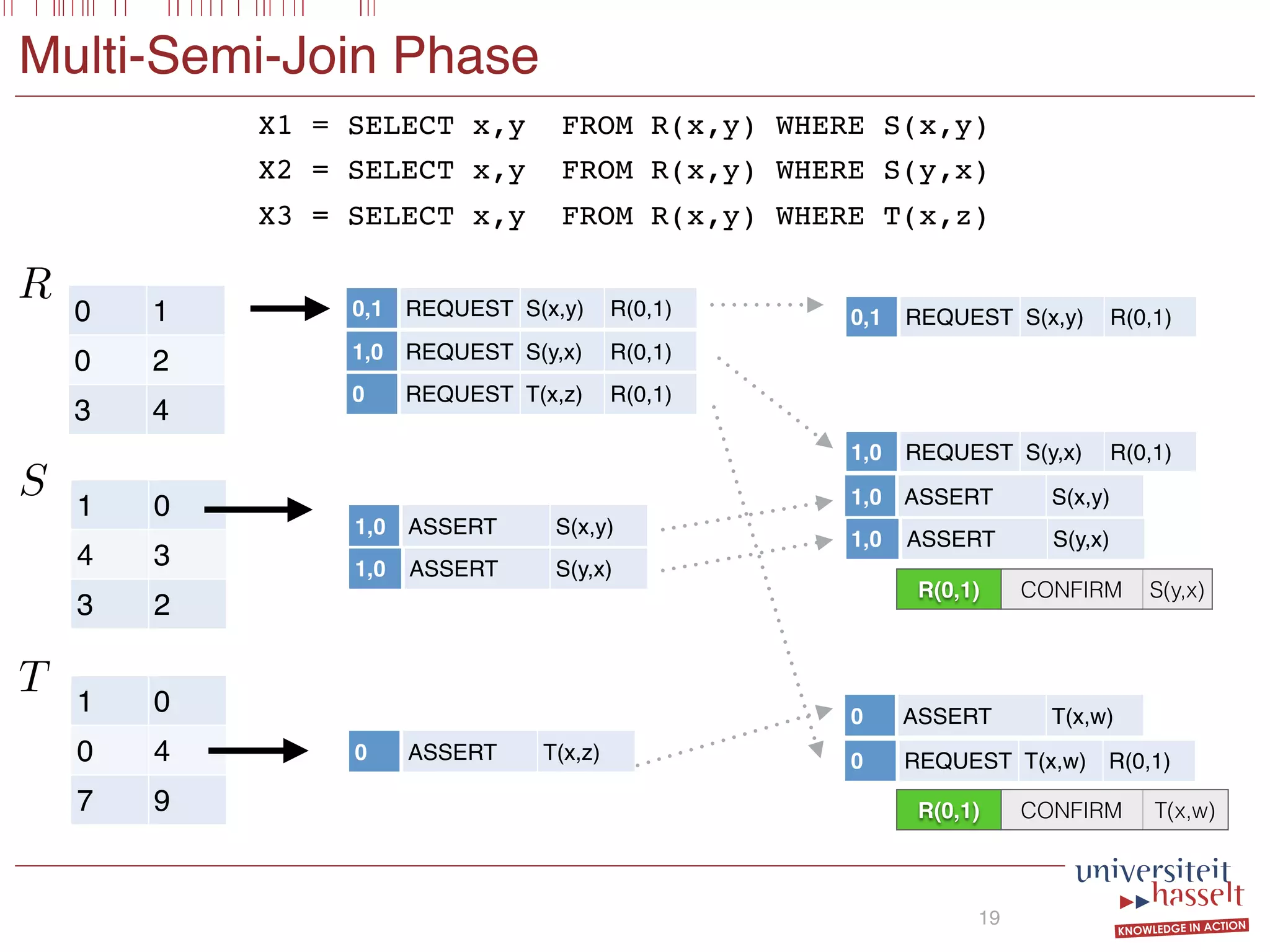
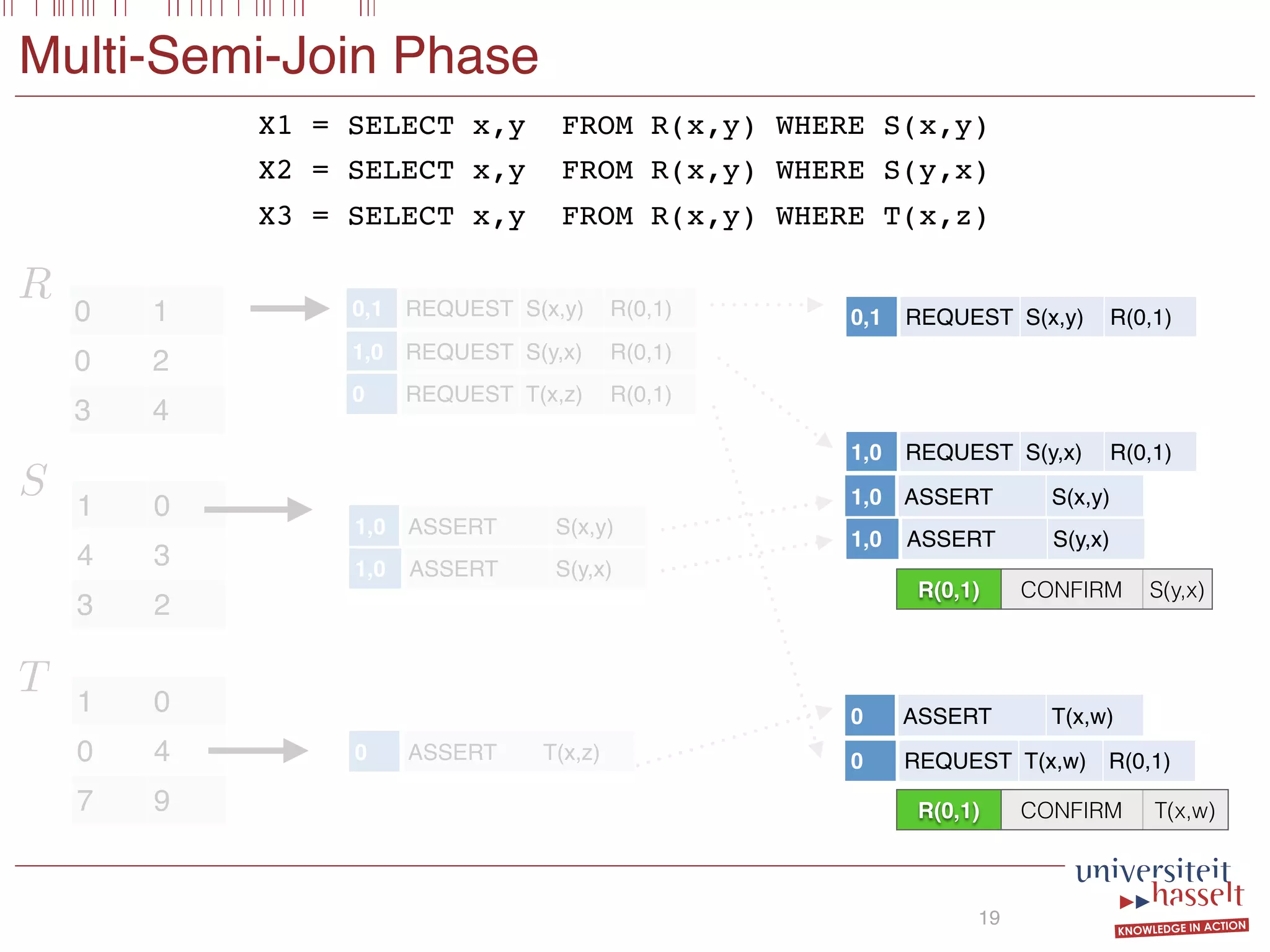
Consider the following SGF query Q:
SELECT (x, y) FROM R(x, y)
WHERE S(x, y) OR S(y, x) AND T(x, z)
Intuitively, this query asks for all pairs (x, y) in R for which
there exists some z such that (1) (x, y) or (y, x) occurs in
S and (2) (x, z) occurs in T. To evaluate Q it suffices to
compute the following semi-joins
X1 := R(x, y) S(x, y);
X2 := R(x, y) S(y, x);
X3 := R(x, y) T(x, z);
store the results in the binary relations X1, X2, or X3, and
subsequently compute ϕ := (X1 ∪X2)∩X3. Our multi-semi-
join operator MSJ(S) (defined in Section 4.2) takes a number
of semi-join-equations as input and exploits commonalities
between them to optimize evaluation. In our framework, a
possible query plan for query Q is of the form:
EVAL(R, ϕ)
MSJ(X1, X2) MSJ(X3)
X1 = SELECT x,y FROM R(x,y) WHERE S(x,y)
X2 = SELECT x,y FROM R(x,y) WHERE S(y,x)
X3 = SELECT x,y FROM R(x,y) WHERE T(x,z)
SELECT x,y FROM R(x,y)
WHERE [X1(x,y) OR X2(x,y)] AND X3(x,y)
Semi-Joins
Boolean
Combination

27. Multi-Semi-Join Phase
19
0 1
0 2
3 4
1 0
4 3
3 2
0,1 REQUEST S(x,y) R(0,1)
1,0 REQUEST S(y,x) R(0,1)
0 REQUEST T(x,z) R(0,1)
1,0 ASSERT S(x,y)
1,0 ASSERT S(y,x)
1 0
0 4
7 9
0 ASSERT T(x,z)
0,1 REQUEST S(x,y) R(0,1)
1,0 REQUEST S(y,x) R(0,1)
1,0 ASSERT S(x,y)
1,0 ASSERT S(y,x)
0 ASSERT T(x,w)
0 REQUEST T(x,w) R(0,1)
R(0,1) CONFIRM S(y,x)
R(0,1) CONFIRM T(x,w)
X1 = SELECT x,y FROM R(x,y) WHERE S(x,y)
X2 = SELECT x,y FROM R(x,y) WHERE S(y,x)
X3 = SELECT x,y FROM R(x,y) WHERE T(x,z)
R
S
T

28. Multi-Semi-Join Phase
19
0 1
0 2
3 4
1 0
4 3
3 2
0,1 REQUEST S(x,y) R(0,1)
1,0 REQUEST S(y,x) R(0,1)
0 REQUEST T(x,z) R(0,1)
1,0 ASSERT S(x,y)
1,0 ASSERT S(y,x)
1 0
0 4
7 9
0 ASSERT T(x,z)
0,1 REQUEST S(x,y) R(0,1)
1,0 REQUEST S(y,x) R(0,1)
1,0 ASSERT S(x,y)
1,0 ASSERT S(y,x)
0 ASSERT T(x,w)
0 REQUEST T(x,w) R(0,1)
R(0,1) CONFIRM S(y,x)
R(0,1) CONFIRM T(x,w)
X1 = SELECT x,y FROM R(x,y) WHERE S(x,y)
X2 = SELECT x,y FROM R(x,y) WHERE S(y,x)
X3 = SELECT x,y FROM R(x,y) WHERE T(x,z)
R
S
T

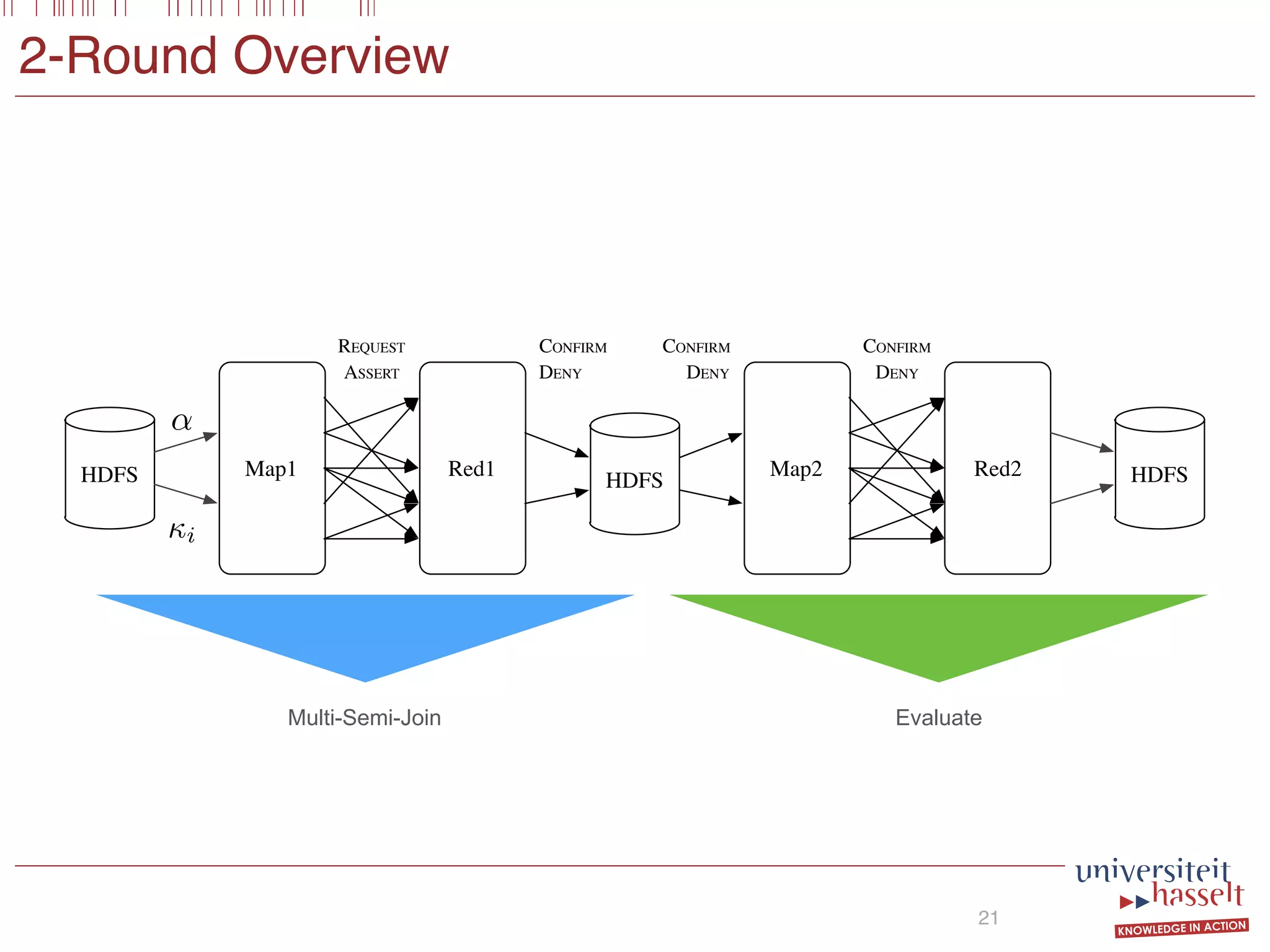
29. EVAL Phase
20
R(0,1) CONFIRM S(y,x)
R(0,1) DENY S(x,y)
R(0,1) CONFIRM T(x,z)
R(3,4) CONFIRM S(y,x)
R(0,2) DENY S(y,x)
R(0,2) DENY S(x,y)
R(0,2) CONFIRM T(x,z)
R(3,4) DENY S(x,y)
R(3,4) DENY T(x,w)
R(0,1) CONFIRM S(y,x)
R(0,1) CONFIRM T(x,z)
R(3,4) CONFIRM S(y,x)
R(0,2) CONFIRM T(x,z)
(False _ True) ^ True ⌘ True
Z(0, 1)output
SELECT x,y FROM R(x,y)
WHERE [S(x,y) OR S(y,x)] AND T(x,z)
Implicit

30. 2-Round Overview
21
HDFS HDFS
Map1 Red1 HDFSMap2 Red2
↵
i
ASSERT
REQUEST CONFIRM CONFIRM CONFIRM
DENY DENY DENY
Multi-Semi-Join Evaluate

31. Some Optimizations
• Tuple IDs & Atom IDs
– Refer to tuple address using
– file id + byte offset
22
1 REQUEST S(y,z) R(0,1) 1 T.1 A.1 #1.043
• Packing
1 REQUEST S(y,z) R(0,1)
1 REQUEST T(x,z) R(0,1)
1 ASSERT S(z,y)
1 ASSERT S(y,z)
1 REQUEST S(y,z) T(x,z) R(0,1)
1 ASSERT S(y,z) S(z,y)
Only key contains actual values
Multiple atoms

32. Some Optimizations
• Tuple IDs & Atom IDs
– Refer to tuple address using
– file id + byte offset
22
1 REQUEST S(y,z) R(0,1) 1 T.1 A.1 #1.043
• Packing
1 REQUEST S(y,z) R(0,1)
1 REQUEST T(x,z) R(0,1)
1 ASSERT S(z,y)
1 ASSERT S(y,z)
1 REQUEST S(y,z) T(x,z) R(0,1)
1 ASSERT S(y,z) S(z,y)
Only key contains actual values
Multiple atoms

33. Some Optimizations
• Tuple IDs & Atom IDs
– Refer to tuple address using
– file id + byte offset
22
1 REQUEST S(y,z) R(0,1) 1 T.1 A.1 #1.043
• Packing
1 REQUEST S(y,z) R(0,1)
1 REQUEST T(x,z) R(0,1)
1 ASSERT S(z,y)
1 ASSERT S(y,z)
1 REQUEST S(y,z) T(x,z) R(0,1)
1 ASSERT S(y,z) S(z,y)
Only key contains actual values
Multiple atoms

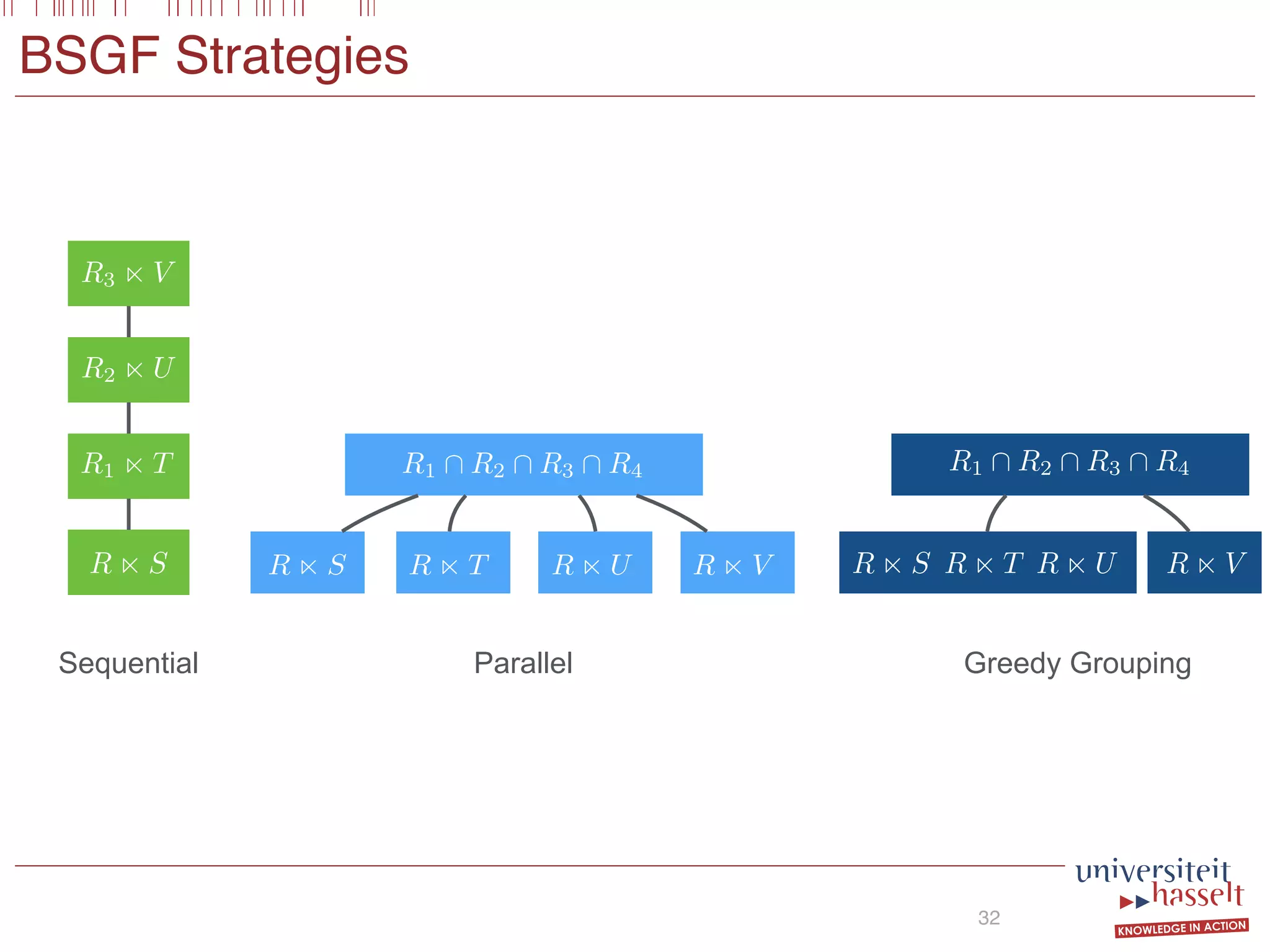
34. Optimal Plan (BSGF)
23
136 Parallel Evaluation of Multi-Semi-Joins
EVAL
Z := X1 ^ (X2 _ ¬X3)
MSJ
X1 := R(x, y) n S(x, z)
MSJ
X2 := R(x, y) n T(y)
MSJ
X3 := R(x, y) n U(x)
(a)
EVAL
Z := X1 ^ (X2 _ ¬X3)
MSJ
X1 := R(x, y) n S(x, z)
X3 := R(x, y) n U(x)
MSJ
X2 := R(x, y) n T(y)
(b)
EVAL
Z := X1 ^ (X2 _ ¬X3)
MSJ
X1 := R(x, y) n S(x, z)
X2 := R(x, y) n T(y)
X3 := R(x, y) n U(x)
(c)
Figure 4.5: Some MapReduce query plan alternatives for the query given in
Example 4.13.
such that its total cost as computed in Equation (4.12) is minimal. The Scan-
Shared Optimal Grouping, which is known to be np-hard, is reducible to
this problem (see Nykiel et al. [139]). Stating it formally, we have:
Theorem 4.14. The decision variant of BSGF-Opt is np-complete.
136 Parallel Evaluation of Multi-Semi-Joins
EVAL
Z := X1 ^ (X2 _ ¬X3)
MSJ
X1 := R(x, y) n S(x, z)
MSJ
X2 := R(x, y) n T(y)
MSJ
X3 := R(x, y) n U(x)
(a)
EVAL
Z := X1 ^ (X2 _ ¬X3)
MSJ
X1 := R(x, y) n S(x, z)
X3 := R(x, y) n U(x)
MSJ
X2 := R(x, y) n T(y)
(b)
EVAL
Z := X1 ^ (X2 _ ¬X3)
MSJ
X1 := R(x, y) n S(x, z)
X2 := R(x, y) n T(y)
X3 := R(x, y) n U(x)
(c)
Figure 4.5: Some MapReduce query plan alternatives for the query given in
Example 4.13.
such that its total cost as computed in Equation (4.12) is minimal. The Scan-
136 Parallel Evaluation of Multi-Semi-Joins
EVAL
Z := X1 ^ (X2 _ ¬X3)
MSJ
X1 := R(x, y) n S(x, z)
MSJ
X2 := R(x, y) n T(y)
MSJ
X3 := R(x, y) n U(x)
(a)
EVAL
Z := X1 ^ (X2 _ ¬X3)
MSJ
X1 := R(x, y) n S(x, z)
X3 := R(x, y) n U(x)
MSJ
X2 := R(x, y) n T(y)
(b)
EVAL
Z := X1 ^ (X2 _ ¬X3)
MSJ
X1 := R(x, y) n S(x, z)
X2 := R(x, y) n T(y)
X3 := R(x, y) n U(x)
(c)
Figure 4.5: Some MapReduce query plan alternatives for the query given in
Example 4.13.
such that its total cost as computed in Equation (4.12) is minimal. The Scan-

35. Optimal MSJ Grouping
• Nykiel et al., 2010 & Wang et al.,2013
• Cost Model
• NP-Hard
• Greedy Approach
– cost matrix
– group current best option
– repeat
24
R,S(x) R,T(x) G,S(x) G,T(y)
R,S(x) 0 +200 +300 -200
R,T(x) 0 -100 +200
G,S(x) 0 -50
G,T(y) 0
R,S(x)
G,S(x)
R,T(x) G,T(y)
R,S(x)
G,S(x)
0 +100 -200
R,T(x) 0 +100
G,T(y) 0

36. Multiple BSGF
• Set of batch queries
• Same!
• More grouping possibilities
• EVAL remains 1 job
25

37. SGF Queries
Evaluation & Optimization

38. SGF Queries
27
Z n I
H n Q
R n S ^ T
G n S ^ T
BSGF Greedy grouping
1
2
3
1 level = MSJ+EVAL
Level

39. SGF Queries
27
Z n I
H n Q
R n S ^ T
G n S ^ T
BSGF Greedy grouping
1
2
3
1 level = MSJ+EVAL
Level
move?

40. SGF Queries
27
Z n I
H n Q
R n S ^ T
G n S ^ T
BSGF Greedy grouping
Z n I
H n Q
R n S ^ T G n S ^ T1
2
3
1 level = MSJ+EVAL
Level
move?

41. Optimal Plan (SGF)
• Assigning level to BSGF queries
• Dependencies
• Optimize for greedy BSGF (MSJ)
• NP-Hard
• Greedy overlap algorithm
28
Z n I
H n Q
R n S ^ T G n S ^ T1
2
3

42. Experimental Evaluation
using Gumbo

43. Set-up
VSC (Flemish Supercomputer Centre)
10 nodes (2x 10-core, 64GB RAM each)
Hadoop 2.6.2, Hive 1.2.1, Pig 0.15.0
Gumbo 0.4
30
http://github.com/JonnyDaenen/Gumbo

44. BSGF Queries
31
QID Query Type of query
A1 R(x, y, z, w)
S(x) ∧ T (y) ∧ U(z) ∧ V (w)
guard sharing
A2 R(x, y, z, w)
S(x) ∧ S(y) ∧ S(z) ∧ S(w)
guard & con-
ditional name
sharing
A3 R(x, y, z, w)
S(x) ∧ T (x) ∧ U(x) ∧ V (x)
guard & condi-
tional key shar-
ing
A4 R(x, y, z, w)
S(x) ∧ T (y) ∧ U(z) ∧ V (w)
G(x, y, z, w)
W (x) ∧ X(y) ∧ Y (z) ∧ Z(w)
no sharing
A5 R(x, y, z, w)
S(x) ∧ T (y) ∧ U(z) ∧ V (w)
G(x, y, z, w)
S(x) ∧ T (y) ∧ U(z) ∧ V (w)
conditional
name sharing
B1 R(x, y, z, w)
S(x) ∧ T (x) ∧ U(x) ∧ V (x) ∧
S(y) ∧ T (y) ∧ U(y) ∧ V (y) ∧
S(z) ∧ T (z) ∧ U(z) ∧ V (z) ∧
large conjunc-
tive query

45. BSGF Strategies
32
Sequential Parallel Greedy Grouping
R2 n U
R3 n V
R1 n T
R n S R n S R n T R n U R n V
R1 R2 R3 R4
R n S R n T R n U R n V
R1 R2 R3 R4

46. 50%
100%
150%
200%
NetTime
SEQ
100%
100%
100%
100%
100%
PAR
59%
54%
68%
63%
63%
GREEDY
60%
98%
56%
60%
74%
1-ROUND
43%
100%
200%
300%
400%
TotalTime
100%
100%
100%
100%
100%
253%
242%
245%
191%
265%
238%
170%
149%
168%
186%
120%
100%
200%
300%
400%
Input
100%
100%
100%
100%
100%
240%
240%
240%
240%
291%
171%
110%
120%
132%
139%
70%
50%
100%
150%
200%
250%
A1 A2 A3 A4 A5
Communication
100%
100%
100%
100%
100%
133%
133%
133%
133%
161%
133%
108%
90%
120%
124%
70%
BSGF Queries
33
~30% faster w.r.t. SEQ
~30% cheaper w.r.t. PAR
same
names
same
keys
no
sharing
duplicate
atoms
standard

47. 50%
100%
150%
200%
NetTime
SEQ
100%
100%
100%
100%
100%
PAR
59%
54%
68%
63%
63%
GREEDY
60%
98%
56%
60%
74%
1-ROUND
43%
100%
200%
300%
400%
TotalTime
100%
100%
100%
100%
100%
253%
242%
245%
191%
265%
238%
170%
149%
168%
186%
120%
100%
200%
300%
400%
Input
100%
100%
100%
100%
100%
240%
240%
240%
240%
291%
171%
110%
120%
132%
139%
70%
50%
100%
150%
200%
250%
A1 A2 A3 A4 A5
Communication
100%
100%
100%
100%
100%
133%
133%
133%
133%
161%
133%
108%
90%
120%
124%
70%
BSGF Queries
33
~30% faster w.r.t. SEQ
~30% cheaper w.r.t. PAR
same
names
same
keys
no
sharing
duplicate
atoms
standard
Replication

48. 50%
100%
150%
200%
NetTime
SEQ
100%
100%
100%
100%
100%
PAR
59%
54%
68%
63%
63%
GREEDY
60%
98%
56%
60%
74%
1-ROUND
43%
100%
200%
300%
400%
TotalTime
100%
100%
100%
100%
100%
253%
242%
245%
191%
265%
238%
170%
149%
168%
186%
120%
100%
200%
300%
400%
Input
100%
100%
100%
100%
100%
240%
240%
240%
240%
291%
171%
110%
120%
132%
139%
70%
50%
100%
150%
200%
250%
A1 A2 A3 A4 A5
Communication
100%
100%
100%
100%
100%
133%
133%
133%
133%
161%
133%
108%
90%
120%
124%
70%
BSGF Queries
33
~30% faster w.r.t. SEQ
~30% cheaper w.r.t. PAR
same
names
same
keys
no
sharing
duplicate
atoms
standard
Replication

49. PIG & HIVE
• Parallel plans in Hive/Pig
• Hive Joins
– 238% slower than PAR.
• Hive Semi-joins
– 126% slower than PAR
• Pig
– 254% slower than PAR
34
100%
200%
300%
400%
500%
600%
NetTime
SEQ
100%
100%
100%
100%
100%
PAR
59%
54%
68%
63%
63%
GREEDY
60%
98%
56%
60%
74%
HPAR
241%
243%
129%
208%
465%
HPARS
139%
134%
138%
115%
476%
PPAR
217%
245%
201%
189%
237%
1-ROUND
43%
200%
400%
600%
800%
TotalTime
100%
100%
100%
100%
100%
253%
242%
245%
191%
265%
238%
170%
149%
168%
186%
225%
218%
142%
78%
211%
324%
317%
319%
117%
640%
540%
614%
490%
373%
576%
120%
200%
400%
600%
Input
100%
100%
100%
100%
100%
240%
240%
240%
240%
291%
171%
110%
120%
132%
139%
246%
246%
124%
140%
298%
361%
361%
361%
181%
437%
344%
433%
344%
344%
535%
70%
100%
200%
300%
400%
500%
A1 A2 A3 A4 A5
Communication
100%
100%
100%
100%
100%
133%
133%
133%
133%
161%
133%
108%
90%
120%
124%
202%
202%
122%
101%
244%
322%
322%
322%
161%
389%
304%
304%
304%
304%
367%
70%

50. SGF Queries
35
S(x) ∧ T (y) ∧ U(z) ∧ V (w)
G(x, y, z, w)
W (x) ∧ X(y) ∧ Y (z) ∧ Z(w)
A5 R(x, y, z, w)
S(x) ∧ T (y) ∧ U(z) ∧ V (w)
G(x, y, z, w)
S(x) ∧ T (y) ∧ U(z) ∧ V (w)
conditional
name sharing
B1 R(x, y, z, w)
S(x) ∧ T (x) ∧ U(x) ∧ V (x) ∧
S(y) ∧ T (y) ∧ U(y) ∧ V (y) ∧
S(z) ∧ T (z) ∧ U(z) ∧ V (z) ∧
S(w) ∧ T (w) ∧ U(w) ∧ V (w)
large conjunc-
tive query
B2 R(x, y, z, w)
(S(x)∧¬T (x)∧¬U(x)∧¬V (x))∨
(¬S(x)∧T (x)∧¬U(x)∧¬V (x))∨
(S(x) ∧ ¬T (x) ∧ U(x) ∧ ¬V (x)) ∨
(¬S(x) ∧ ¬T (x) ∧ ¬U(x) ∧ V (x))
uniqueness
query
Table 2: Queries used in the BSGF-experiment
restricted to only disjunction and negation. The same
optimization also works for multiple BSGF queries. We
refer to these programs as 1-ROUND below.

51. 50%
100%
150%
NetTime
SEQ
100%
100%
PAR
22%
44%
GREEDY
17%
36%
1-ROUND
18%
100%
300%
500%
TotalTime
100%
100%
361%
43%
106%
27%
17%
100%
300%
500%
700%
Input
100%
100%
411%
51%
80%
25%
15%
100%
200%
300%
400%
B1 B2
Communication
Values relative to SEQ
100%
100%
206%
28%
76%
18%
15%
Large Queries
36
one key
multiple relation
multiple
key/relation

52. 50%
100%
150%
NetTime
SEQ
100%
100%
PAR
22%
44%
GREEDY
17%
36%
1-ROUND
18%
100%
300%
500%
TotalTime
100%
100%
361%
43%
106%
27%
17%
100%
300%
500%
700%
Input
100%
100%
411%
51%
80%
25%
15%
100%
200%
300%
400%
B1 B2
Communication
Values relative to SEQ
100%
100%
206%
28%
76%
18%
15%
Large Queries
36
70% cheaper
than PAR
only 6% more expensive
than SEQ
83% faster
than SEQ
one key
multiple relation
multiple
key/relation

53. 50%
100%
150%
NetTime
SEQ
100%
100%
PAR
22%
44%
GREEDY
17%
36%
1-ROUND
18%
100%
300%
500%
TotalTime
100%
100%
361%
43%
106%
27%
17%
100%
300%
500%
700%
Input
100%
100%
411%
51%
80%
25%
15%
100%
200%
300%
400%
B1 B2
Communication
Values relative to SEQ
100%
100%
206%
28%
76%
18%
15%
Large Queries
36
70% cheaper
than PAR
only 6% more expensive
than SEQ
83% faster
than SEQ 64% faster than SEQ
82% faster than SEQ
37% cheaper than PAR
73% cheaper than SEQ
60% cheaper than PAR
83% cheaper than SEQ
one key
multiple relation
multiple
key/relation

54. 50%
100%
150%
200%
250%
300%
NetTime
SEQ
100%
100%
PAR
22%
44%
GREEDY
17%
36%
HIVE
83%
69%
PIG
44%
131%
1-ROUND
18%
100%
300%
500%
700%
900%
1100%
TotalTime
100%
100%
361%
43%
106%
27%
844%
61%
560%
87%
17%
100%
300%
500%
700%
900%
Input
100%
100%
411%
51%
80%
25%
749%
80%
653%
73%
15%
100%
300%
500%
700%
900%
B1 B2
Communication
Values relative to SEQ
100%
100%
206%
28%
76%
18%
620%
67%
323%
63%
18%
Gumbo vs. PIG & HIVE
37

55. SGF Queries
38
(a) Query Set C1
Z4(¯x) := G(¯x) Z1(x) ∧ Z1(y)
Z1(¯x) := R(¯x) S(x) ∧ S(y)
Z5(¯x) := H(¯x) Z2(x) ∧ Z2(y)
Z2(¯x) := G(¯x) T(x) ∧ T(y)
Z6(¯x) := R(¯x) Z3(x) ∧ Z3(y)
Z3(¯x) := H(¯x) U(x) ∧ U(y)
(b) Query Set C2
Z31(z) := I(¯x) Z22(x) ∧ T(x) ∧ V (y)
Z21(z) := G(¯x) Z11(x) ∧ U(y)
Z11(z) := R(¯x) S(x) ∧ T(y)
Z22(z) := H(¯x) U(y) ∨ V (y) ∧ Z12(x)
Z12(z) := R(¯x) T(y)
Z23(z) := R(¯x) U(x) ∧ T(y) ∧ V (z) ∧ Z13(w)
Z13(z) := I(¯x) ¬S(w)
(c) Query C3
Z21(¯x) := H(¯x) Z11(x) ∨ Z12(y) ∨ Z23(z) ∨ Z24(w)
Z11(y) := R(¯x) S(x) ∨ T(y)
Z12(y) := R(¯x) U(z) ∨ S(x)
Z13(y) := G(¯x) U(x) ∨ V (y)
Z14(y) := G(¯x) S(z) ∨ U(x)

56. SGF Queries
39
PAR 50% faster w.r.t. SEQ
42% faster w.r.t. SEQ
(but 28% higher than PAR)
30% cheaper
w.r.t. PAR/SEQ
50%
100%
150%
200%
NetTime
SEQ-UNIT
100%
100%
100%
100%
PAR-UNIT
31%
51%
73%
32%
GREEDY-SGF
56%
71%
78%
42%
50%
100%
150%
200%
TotalTime
100%
100%
100%
100%
107%
121%
108%
67%
58%
74%
92%
57%50%
100%
150%
200%
Input
100%
100%
100%
100%
104%
108%
100%
79%
52%
61%
64%
50%
50%
100%
150%
200%
C1 C2 C3 C4
Communication
100%
100%
100%
100%
105%
105%
95%
76%
69%
79%
85%
72%

57. Conclusions
& Future Work

58. Conclusion
• What?
– SGF Query evaluation in MapReduce
– Quick results at low cost (Cloud)
• Why?
– Easy, but still expressive
– Power more complex engines (SJ reducers, etc.)
• How?
– MSJ operator
– Cost-based Grouping (BSGF)
– Level-Assignment (SGF)
• When?
– lots of overlapping subqueries
41

59. General Contributions
• MapReduce
– cost model refinements
– general optimizations
• Gumbo
– Request Response
– beats Pig and Hive
42

60. Future Work
• Skew
• Spark: update cost model
• Study optimization effects
• Rules for subclasses
• Incorporate into existing systems
• Get Gumbo on GitHub!
• More details? poster session tomorrow @2PM!
43

61. The end…
44
Thank you!
http://github.com/JonnyDaenen/Gumbo