This document summarizes key aspects of variational autoencoders (VAEs): VAE is a generative model that learns a latent representation of data. It approximates the intractable posterior using an encoder network and maximizes a variational lower bound. Semi-supervised VAE models can incorporate unlabeled data by learning shared representations. VAEs have been extended for recurrent sequences, convolutional structures, disentangled representations, and multi-modal data. Importance weighted autoencoders provide a tighter evidence lower bound than standard VAEs.

1. Chapter 6
Deep generative models
6.1 ∼ 6.2

2. 6.1 Variational autoencoder
• Generative model
p(zn) = 𝒩(zn ∣ 0, I),
p(xn ∣ zn, W) = 𝒩 (xm ∣ f(zn; W), λ−1
x I)
(6.1)
(6.2)
f : generative network or decoder
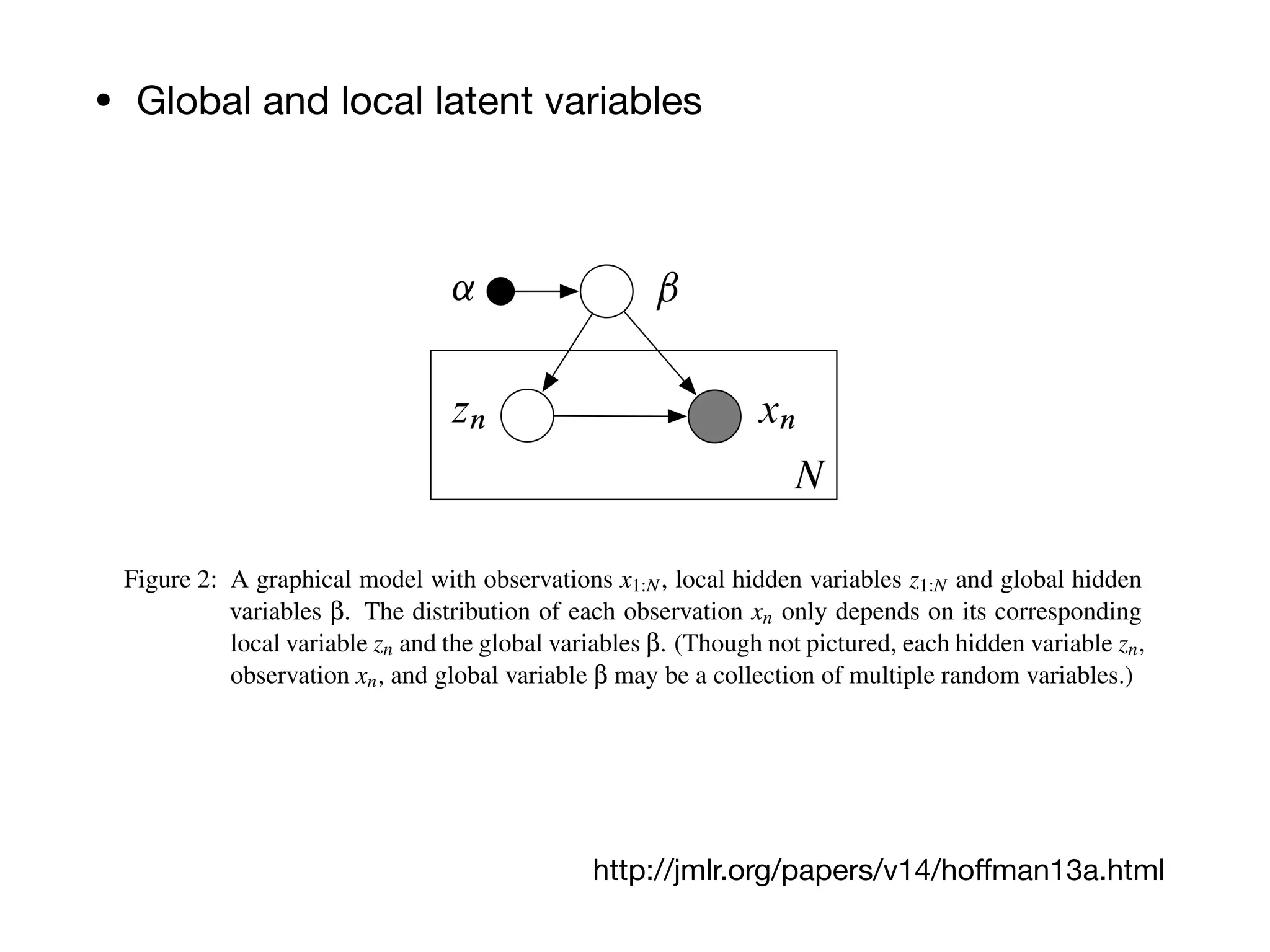
• Posterior and objective
p(Z, W ∣ X) =
p(W)∏
N
n=1
p(xn ∣ zn, W)p(zn)
p(X)
(6.3)
DKL [q(Z, W) ∣ p(Z, W|X)] (6.4)
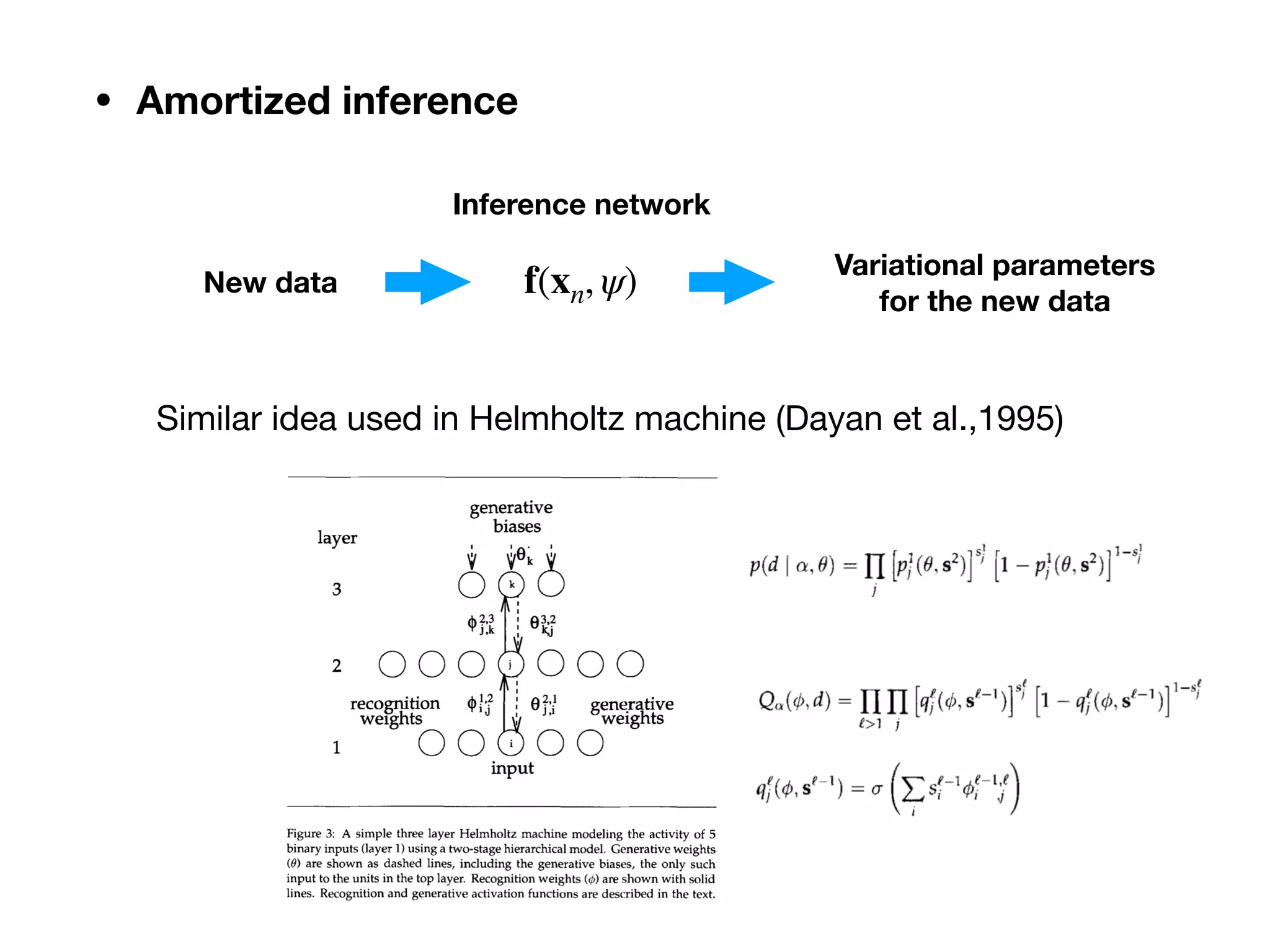
6.1.1 Generative and inference networks
6.1.1.1 Generative model and posterior approximation

3. • Mean-field approximation
q(Z, W; X, ψ, ξ) = q(Z; X, ψ)q(W; ξ) (6.5)
q(W; ξ) = 𝒩
∏
i,j,l
(w(l)
i,j
∣ m(l)
i,j
, v(l)
i,j
) (6.6)
q(Z; X, ψ) =
N
∏
n=1
q(zn; xn, ψ)
=
N
∏
n=1
𝒩 (zn ∣ m(xn; ψ), diag(v(xn; ψ))) (6.7)
f(xn, ψ) = (m(xn; ψ), ln(v(xn; ψ))) (6.8)
f : inference (recognition) network or encoder

4. • Amortized inference
f(xn, ψ)New data
Variational parameters
for the new data
Inference network
Similar idea used in Helmholtz machine (Dayan et al.,1995)

5. http://jmlr.org/papers/v14/hoffman13a.html
• Global and local latent variables

6. DKL [q(Z, W; X, ϕ, ξ) ∥ p(Z, W|X)]
= − {E[ln p(X, Z, W)] − E[ln q(Z; X, ψ)] − E[ln q(W; ξ)]} + ln p(X)
(6.9)
∴ ln p(X) − DKL [q(Z, W; X, ϕ, ξ) ∥ p(Z, W|X)]
= E[ln p(X, Z, W)] − E[ln q(Z; X, ψ)] − E[ln q(W; ξ)]
= ℒ(ψ, ξ) (6.10)
Maximize w.r.t. andℒ(ψ, ξ) ψ ξ
(6.11)
ℒ 𝒮(ψ, ξ)
=
N
M ∑
n∈𝒮
{E[ln p(xn ∣ zn, W)] + E[ln p(zn)] − E[ln q(zn)]}+
E[ln p(W)] − E[ln q(W; ξ)]
6.1.1.2 Training by variational inference

7. • Gradients of parameters
∇ξℒ 𝒮(ψ, ξ)
=
N
M ∑
n∈𝒮
∇ξE[ln p(xn ∣ zn, W)] + ∇ξE[ln p(W)] − ∇ξE[ln q(W)]
(6.12)
∇ψ ℒ 𝒮(ψ, ξ)
=
N
M ∑
n∈𝒮
{∇ψ E[ln p(xn ∣ zn, W)] + ∇ψ E[ln p(zn)] − ∇ψ E[ln q(zn)]}
(6.13)
ξ : variational parameter of q(W; ξ)
ψ : inference network parameter of f(xn; ψ)

8. Labelled data 𝒟 𝒜 = {X 𝒜, Y 𝒜}
Un-labelled data 𝒟 𝒰 = X 𝒰
6.1.2.1 M1 model
1. Train encoder and decoder with
2. Train supervised model with
{X 𝒜, X 𝒰}
{Z 𝒜, Y 𝒜}
where is encoded from with the model of 1.Z 𝒜 X 𝒜
6.1.2 Semi-supervised models

9. 6.1.2.2 M2 model
X 𝒜
Y 𝒜 Z 𝒜
W X 𝒰
Z 𝒰Y 𝒰
• Generative process with shared parameter (and shared
prior on and
W
p(Y) p(Z)
p(X 𝒜, X 𝒰, Y 𝒜, Y 𝒰, Z 𝒜, Z 𝒰, W)
= p(X 𝒜 |Y 𝒜, Z 𝒜)p(Y 𝒜)p(Z 𝒜)p(X 𝒰 |Y 𝒰, Z 𝒰)p(Y 𝒰)p(Z 𝒰) (6.14)

10. • Approximate posterior
q(Z 𝒜; X 𝒜, Y 𝒜, ψ) =
∏
n∈𝒜
𝒩(zn |m(xn, yn; ψ), diagm(v(xn, yn; ψ))) (6.15)
q(Z 𝒰; X 𝒰, ψ) =
∏
n∈𝒰
𝒩(zn |m(xn; ψ), diagm(v(xn; ψ)) (6.16)
q(Y 𝒰; X 𝒰, ψ) =
∏
n∈𝒰
Cat(yn |π(xn; ψ)) (6.17)
m, v, π : inference networks parametrized with ψ
q(W; ξ) : Gaussian distribution parametrized with ξ

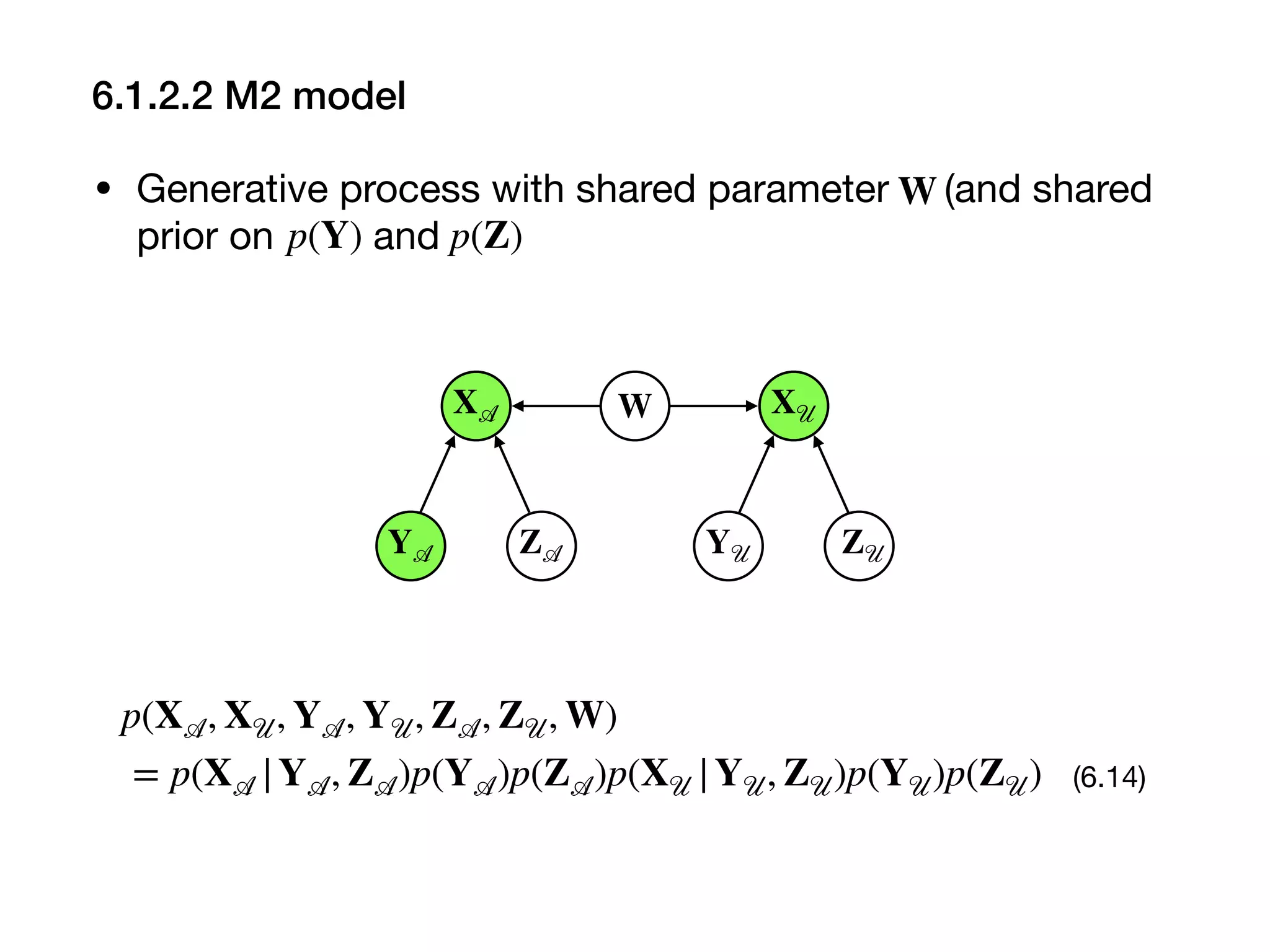
11. • KL-divergence
DKL[q(Y 𝒰, Z 𝒜, Z 𝒰, W; X 𝒜, Y 𝒜, X 𝒰, ξ, ψ ∥ p(Y 𝒰, Z 𝒜, Z 𝒰, W ∣ X 𝒜, X 𝒰, Y 𝒜)]
= ℱ(ξ, ψ) + const . (6.18)
ℱ(ξ, ψ) = ℒ 𝒜(X 𝒜, Y 𝒜; ξ, ψ) + ℒ 𝒰(X 𝒰; ξ, ψ) − DKL[q(W; ψ) ∥ p(W)] (6.19)
ℒ 𝒜(X 𝒜, Y 𝒜; ξ, ψ)
= E[ln p(X 𝒜 |Y 𝒜, Z 𝒜, W)] + E[ln p(Z 𝒜)] − E[ln q(Z 𝒜; X 𝒜, Y 𝒜, ψ)] (6.20)
ℒ 𝒰(X 𝒰; ξ, ψ) = E[ln p(X 𝒰 |Y 𝒰, Z 𝒰, W)] + E[ln p(Y 𝒰)] + E[ln p(Z 𝒰)]
−E[ln q(Y 𝒰; X 𝒰, ψ)] − E[ln q(Z 𝒰; X 𝒰, ψ)]
(6.21)
• Maximize w.r.t. andℱ(ξ, ψ) ξ ψ

12. • Extension of objective function to use labelled data with a
classification likelihood
ℱβ(ξ, ψ) = ℱ(ξ, ψ) + β ln q(Y 𝒜; X 𝒜, ψ) (6.22)
β : weight of classification likelihood

13. 6.1.3 Applications and extensions
6.1.3.1 Extension of models
• Incorporate recurrent network and attention (DRAW)
• Convolutional VAE
• Disentangle representation learning
• Multi-modal learning with shared latent representation
(e.g., images and texts)
https://jhui.github.io/2017/04/30/DRAW-Deep-recurrent-attentive-writer/
Explanation of DRAW with python implementation:

14. 6.1.3.2 Importance weighted AE
ℒT = Ez(t)∼q(z(t))
[
ln
1
T
T
∑
t=1
p(x, z(t)
)
q(z(t); x) ]
≤ ln Ez(t)∼q(z(t))
[
1
T
T
∑
t=1
p(x, z(t)
)
q(z(t); x)]
= ln Ez(t)∼q(z(t))
[
1
T
T
∑
t=1
p(x|z(t)
)
p(z(t)
)
q(z(t); x) ]
= ln p(x)
(6.23)
• Equivalent to ELBO when T=1
• Larger T is, tighter the bound (appendix A in the paper):
ln p(x) ≥ ⋯ ≥ ℒt+1 ≥ ℒt ≥ ⋯ℒ1 = ℒ (6.24)