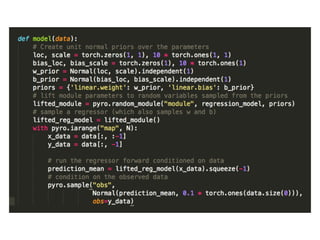
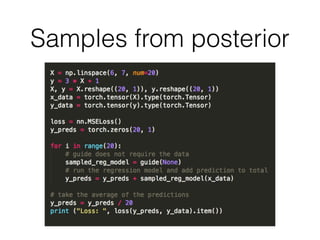
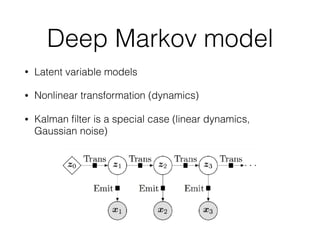
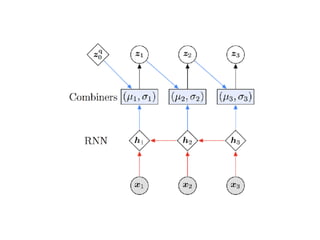
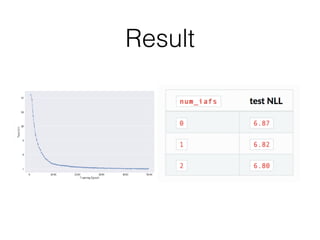
Probabilistic programming with Pyro (1) introduces Pyro, a probabilistic programming language based on PyTorch that allows defining probabilistic models and performing Bayesian inference; (2) discusses Bayesian modeling and inference using linear regression as an example; (3) presents an example of using Pyro to build a deep Markov model for modeling music sequences.

1. Probabilistic
programming with Pyro
July 22, 2018 大江橋Pythonの会
Taku Yoshioka

2. • What is Pyro?
• Introduction to Bayesian modeling
• Example 1: linear regression
• Bayesian inference with Pyro
• Example 2: deep Markov model for music

3. Pyro
• Probabilistic programing language (library); PPL
• Pytorch
• Uber
• Universal, Scalable, Minimal, Flexible

4. Why PPL?
https://www.youtube.com/watch?v=ATaMq62fXno

5. Why PPL?
Taniguchi et al., Online Spatial Concept and Lexical Acquisition with
Simultaneous Localization and Mapping

8. • How to make the model for your problem?
• How to do inference on the model given the data?
• How to implement the model for inference?

9. Bayesian inference
Model Prior
Posterior
Marginal probability (evidence)
Given model and prior, Pyro infers posterior
p(⇥|D) =
p(D|⇥)p(⇥)
p(D)
: Data⇥ : Model parameterD

10. Linear regression
y = Wx + b + ✏

11. Bayesian linear regression
D = {x, y}⇥ = {W, b}
y = Wx + b + ✏
p(W, b|x, y) =
p(y|W, b, x)p(W, b)
p(y|x)
p(W, b) = p(W)p(b)

12. I.I.D. samples
p(D|W, b) =
MY
i=1
p(yi|W, b, xi)
log p(D|W, b) =
MX
i=1
log p(yi|W, b, xi)
p(yi|W, b, xi) = N(Wx + b, I)
log p(D|W, b) /
MX
i=1
||yi (Wxi + b)||2

13. Marginal predictive
distribution
PosteriorModel
¯˜y =
Z
˜yp(˜y|W, b, ˜x)p(W, b|D)dWdbd˜y
p(˜y|˜x) =
Z
p(˜y|W, b, ˜x)p(W, b|D)dWdb
⇡ N 1
NX
i=1
˜yi
˜yi ⇠ p(˜yi|Wi, bi, ˜x)
Wi, bi ⇠ p(Wi, bi|D)

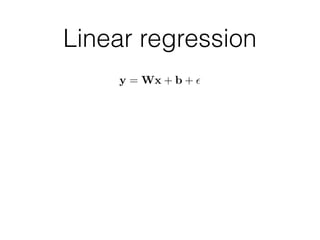
14. Posterior approximation
• Referred to as variational distribution (‘guide’ in Pyro)
• Minimize wrt
p(W, b|D) ⇡ q (W, b)
p(W, b|D) ⇡ q W
(W)q b
(b)Simple version
KL [q (W, b)||p(W, b|D)]

15. Evidence lower bound
(ELBO)
L( ) = Eq (⇥) [log p(D, ⇥) log q (⇥)]
= log p(D) KL [q (W, b)||p(W, b|D)]
 log p(D)
Maximizing ELBO implies minimizing KL-divergence

16. Monte Carlo (MC)
approximation
Eq (⇥) [log p(D, ⇥) log q (⇥)]
= N 1
NX
i=1
[log p(D, ⇥i) log q (⇥i)] ⇥i ⇠ q (⇥i)
• Reparametrization is applied to reduce the variance of
stochastic gradient: https://stats.stackexchange.com/
questions/199605

17. Stochastic variational
inference
1. Draw samples of the RVs in the model
2. Compute ELBO with Monte Carlo approximation
3. Compute stochastic gradient of ELBO wrt
parameters
4. Apply a gradient descent algorithm
5. Back to 1.

18. Bayesian inference with Pyro
1. Prepare data
2. Implement model and guide
3. Run SVI
4. Draw samples from posterior for prediction

19. Model

21. Guide

22. SVI

23. Samples from posterior

24. Probabilistic model of music
• Model polyphonic music
• Sequences of 88 dimensional binary vectors
• Nonlinear dynamics
• Different length

25. Deep Markov model
• Latent variable models
• Nonlinear transformation (dynamics)
• Kalman filter is a special case (linear dynamics,
Gaussian noise)

26. Full probability
p(x1:T , z0:T ) = p(z0)
TY
t=1
p(xt|zt)p(zt|zt 1)
Emmision Transition

27. Emitter

28. Gated transition

29. Model

30. Amortized inference
• Instead of parametrized posterior on the latent RVs,
introduce neural network that mimics the inference
on each of the latent RVs by outputting variational
parameters given the information of other RVs
• Learning-to-learn
• Variational autoencoder (VAE)

32. Guide

33. SVI

34. Result