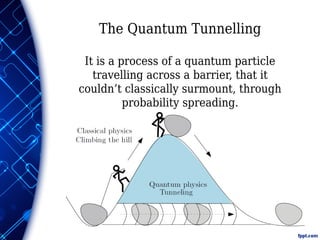
Quantum computers harness quantum mechanics to perform computations by taking advantage of properties like superposition and entanglement. As transistors continue shrinking to the quantum scale, quantum effects like tunneling pose problems for classical computing. Quantum computers represent qubits as quantum states and use gates to manipulate them, allowing multiple computations to occur simultaneously. While challenges remain, quantum computing could solve problems like the travelling salesman problem much faster by exploring many possibilities at once.

1. The Evolution of
Quantum Computers
Subhadra Sundar Chakraborty
CSE/2015/043

2. For most of our history, human
technologies consisted of
brains, fires and sharp sticks.
While these have become
power plants and nuclear
weapons, the greatest
upgrade to our limits of
thinking has happened.

3. Computing powers of our
computers have kept growing
ever since allowing us to build
smaller and more powerful
machines at the same time.

4. Smaller and more compact computers
have smaller transistors which is basically
a switch that either allows or block
information passing through.
Today a typical transistor is 14 nanometres
in size (of the scale of an atom) and an
integrated circuit consists literally billions
of them. However this meets it’s Quantum
Mechanical limits.
Electrons may pass through a blocked
transistor through a process called
Quantum Tunnelling.

5. The Quantum Tunnelling
It is a process of a quantum particle
travelling across a barrier, that it
couldn’t classically surmount, through
probability spreading.

6. We are approaching the physical
limit of how tiny things can get
and the limit is Quantum
Mechanical.
Scientists are trying to use some
of these weird properties of the
Quantum Physics to build a
Quantum Computer

7. In Quantum Mechanics, states of free existing entities
could be represented through state vectors knows as
Dirac kets. Correspondingly, any arbitrary binary
property of a particle could be taken as two different
ket vectors and any such arbitrary particle would have
a wave function as a superposition of the two wave
functions.
Ψ0
=α∗Ψ1
+β∗Ψ2
where α ,βϵC
|Ψa
+Ψb
|2
=(Ψa
+Ψb
)×(Ψa
+Ψb
)=(Ψa
)2
+(Ψb
)2
+Ψa
×Ψb
+Ψb
×Ψa

8. The Quantum Bit (qubit)
In quantum computing, a qubit or quantum bit is a
unit of quantum information—the quantum
analogue of the classical bit. A qubit is a two-state
quantum-mechanical system, such as the
polarization of a single photon: here the two states
are vertical polarization and horizontal
polarization.
In a classical system, a bit would have to be in one
state or the other. However, quantum mechanics
allows the qubit to be in a superposition of both
states at the same time, a property which is
fundamental to quantum computing.

9. Entangled qubits
Two classical bits can be 00 or 01 or 10 or 11. We can ask
the value of the first bit with out affecting the second bit.
Two qubits could be in the state 1/2 (|0> + |1>)
The first qubit is neither |0> nor |1>. It’s not even a
superposition of |0> and |1> because the state is not
separable: the value of the first qubit is entangled with the
value of the second. We can’t discover value of first
qubit without affecting the second.
Say we measure it and get 0;
that means the state of
the system is now |01> and therefore the second qubit is
now |1>. But it wasn’t |1> before; it was entangled with
the first qubit.

11. The Quantum Gate (Quantum Logic Gate)
In quantum computing and specifically the quantum
circuit model of computation, a quantum gate (or
quantum logic gate) is a basic quantum circuit
operating on a small number of qubits. They are the
building blocks of quantum circuits, like classical logic
gates are for conventional digital circuits.

12. The Empirical Constraints
Ψα
=wave− ¨fn−αth
state
1<α≤nfor α,nϵR
P(Ψ
α
)=Ψ
1
×Ψ
1
+Ψ
2
×Ψ
2
+...+Ψ
n
×Ψ
n
for all α ϵR
P'(Ψμ
)=∑μ
‖Ψμ
‖2
=1(μϵW )
∫−∞
+∞
P(X)=∫−∞
+∞
‖Ψ
μ
(X)‖
2
dX=1

13. Types of Quantum Computers
●
One-way Quantum Computers –
Contains highly entangled qubits
●
Adiabatic Quantum Computers –
Executes algorithms through
transformation of Hamiltons whose
ground state contains one or more
solution.
●
Topological Quantum Computers –
Breaks down problems in a 2D
topological space of anyons to crave
for solution.

14. D-Wave System 2X 1000 qubits
Quantum Processor

15. So what are these computers good
in?
●
All hit and trial problems that requires
many (billions and trillions!) options to
be investigated to find out the answer.
●
An example could be Travelling
Salesman Problem
●
Some other applications massive scale
implementation of Dijkstra’s algorithm
and Database search.
●
Simulations of nuclear phenomena (after
all it’s nice to tackle Quantum physics
with actual Quantum physics!)

16. Quantum Computers are indeed the quantum
leap in the field of computing as it allows us
to harness the power of superposition to
explore many options at a time simultanously.
If properly exploited, for some cases
Quantum Computers could be a boon to
humanity.
Thank you.