実験数学3 講義スライド

1. 実験数学 3
(大阪大学理学部数学科 3 年・4 年)
第 2 回: NP 困難性
鈴木 譲
大阪大学
2013 年 4 月 18 日

2. あらまし
P と NP
SAT から 3SAT への多項式時間還元

3. Turing Machine (TM)
S: 有限集合
A : (S ∪ {start}) × {0, 1, ▷, ◁} →
(S ∪ {halt, yes, no}) × {0, 1, ▷, ◁} × {−1, 0, 1}
{xi }T
i=0, mi ≥ 2,
xi = (x
(1)
i = ▷, x
(2)
i ∈ {0, 1}, · · · , x
(mi −1)
i ∈ {0, 1}, xmi
i = ◁)
1. x0 = (x
(1)
0 , · · · , x
(m0)
0 ) [入力], s0 = start, k0 = 1
2. A(si , x
(ki )
i ) = (t, y, d), t ̸∈ {halt, yes, no}
=⇒ si+1 := t, x
(ki )
i+1 := y, ki+1 := ki + d
3. xT = (x
(1)
T , · · · , x
(mT )
T ) [出力], sT ∈ {yes, np, halt}
A の仮定:
{
x
(ki )
i = ▷ =⇒ y = ▷, d ̸= −1
x
(ki )
i = ◁, y ̸= ◁ =⇒ x
(ki +1)
i+1 = ◁

4. s0 = start
si
si+1 = t
sT ∈ {yes,
no, halt}
x
(mi+1−1)
i+1
x
(mi −1)
i
x
(ki −1)
i+1 x
(ki )
i+1x
(ki +1)
i+1
= y
x
(ki )
i
x
(2)
i+1
x
(2)
i
x
(2)
0
x
(mT −1)
Tx
(2)
T
▷ ◁
◁
◁
◁x
(m0)−1
0
↓
↓
↓ ↓ ↓
d = −1 d = 0 d = 1
↓
▷
▷
▷

5. 多項式時間で解く
f : {0, 1}∗ → {0, 1}∗ (halt で終了して、xT を出力)
f : {0, 1}∗ → {0, 1} (yes, no で終了)
A はアルゴリズム
任意の入力 x0 ∈ {▷} × {0, 1}∗ × {◁} について、T < ∞
σ: x0 ∈ {▷} × {0, 1}∗ × {◁} の両端の ▷, ◁ を除いた列
TA: アルゴリズムが A のときの σ ∈ {0, 1}∗ → T ∈ N
入力長が n := |σ| のときのアルゴリズム A の実行時間 Tn,A:
Tn,A := max
σ∈{0,1}n
TA(σ)
アルゴリズム A が多項式時間で解ける
有限個の n を除いて、Tn,A ≤ nk となる k ∈ N が存在

6. 言語の認識
Σ1, Σ0 ⊆ {0, 1}∗, Σ1 ∩ Σ0 = ϕ
Σ := Σ1 ∪ Σ0
言語 Σ の認識
TM のアルゴリズムが
入力 σ ∈ Σ に対し、yes(σ ∈ Σ1) または no(σ ∈ Σ0) で停止
例: Σ = {0, 1}∗
1. σ ∈ {0, 1}∗ の中の 1 の個数が偶数か否か
2. σ ∈ {0, 1}∗ を 2 進数表記とみたときに、素数であるか否か

7. 決定問題と符号化
Π1, Π0: Π1 ∩ Π0 = ϕ, 可算集合
Π := Π1 ∪ Π0 (各要素を事例とよぶ)
φ : Π → Σ ⊆ {0, 1}∗ (単射, 符号化とよぶ)
φ(Π1) ⊆ Σ1, φ(Π0) ⊆ Σ0
決定問題 Π の解決
TM のアルゴリズムが
I ∈ Π に対し、yes(φ(I) ∈ Σ1) または no(φ(I) ∈ Σ0) で停止

8. 決定問題の例: 充足可能性問題 SAT
1. 有限集合 U = {u1, u2, · · · , un} に対して、
t : U → {T, F}
2. t(ui ) = F ⇐⇒ t( ¯ui ) = T なる ¯U = {¯u1, ¯u2, · · · , ¯un} に対し、
t : U ∪ ¯U → {T, F}
3. c ⊆ U ∪ ¯U に対して、
t(c) = T ⇐⇒ t(z) = T for ∃z ∈ c
4. U 上の節集合 C に対して、
t(C) = T ⇐⇒ t(c) = T for ∀c ∈ C
リテラル U ∪ ¯U の要素
節 U ∪ ¯U の部分集合 c (|c|: 節の大きさ、要素数)
節集合 節を要素とする集合

9. 事例： 有限集合 U, U 上の節集合 C
質問： t(C) = T となる t : U → {T, F} が存在するか。
1. U = {u1, u2}, C = {{u1, ¯u2}, {¯u1, u2}} 「存在する」
t(u1) = t(u2) = T なる t に対して t(C) = T。
2. U = {u1, u2}, C = {{u1, u2}, {u1, ¯u2}, {¯u1}} 「存在しない」
t(C) = T なる t が存在しない。

10. 符号化の例
Ψ := {0, 1, −, [, ], (, ), , }
1. x ∈ Z: 非負の数は 2 進、負の数は前に −。
2. [x]: で数値ではなく、識別のための記号。
3. (x1, · · · , xm): x1, · · · , xm からなる列。
Ψ の要素 0 1 − [ ] ( ) ,
2 進列 000 001 010 011 100 101 110 111
1. U = {u1, u2}, C = {{u1, ¯u2}, {¯u1, u2}}:
(([1],[10]),(([1],[-10]),([-1],[10])))
を 2 進列に直した 41 × 3 = 123 ビットが入力の長さ
2. U = {u1, u2}, C = {{u1, u2}, {u1, ¯u2}, {¯u1}}:
([1],[10]),(([1],[10]),([1],[-10]),([-1]))
を 2 進列に直した 48 × 3 = 144 ビットが入力の長さ

11. P と NP
決定性 TM (DTM) 1 個の TM のみを適用
非決定性 TM (NDTM) 任意個の TM を適用
(1 個の TM で si ∈ halt, yes, no になるまで)
P
DTM のアルゴリズムで、多項式時間で解ける決定問題の集合
NP
NTM のアルゴリズムで、多項式時間で解ける決定問題の集合
▶ P ⊆ NP
▶ P ̸= NP であることが強く予想されている

12. 多項式時間還元性
Π, Π′: 決定問題
φ : Π → {0, 1}∗: Π における符号化
φ′ : Π′ → {0, 1}∗: Π′ における符号化
Π は Π′
に多項式時間で還元 (Π ∝ Π′
)
▶ f (φ(Π1)) ⊆ φ′(Π′
1)
▶ f (φ(Π0)) ⊆ φ′(Π′
0)
なる f : φ(Π) → φ′(Π′) を多項式時間で解く (halt で停止)
入力が σ ∈ φ(Π) であれば、
1. f : σ → f (σ) で、時間 TA(σ) ≤ |σ|kA
2. f の出力長 |f (σ)| は、|σ| + TA(σ) を超えない。
(◁ を右に移動させるのに 1 ステップ以上要する)

13. Π ∝ Π′
, Π′
∝ Π′′
=⇒ Π ∝ Π′′
証明:
f ′ : f (φ(Π)) → φ′′(Π′′) 多項式時間還元
B: f ′ のアルゴリズム
1. f ′ : f (σ) → f ′(f (σ)) で、時間 TB(f (σ)) ≤ |f (σ)|kB
2. 全体でも、
T(σ) := TA(σ) + TB(f (σ)) ≤ |σ|kA + (|σ| + |σ|kA )kB
3. T(σ) は、入力長 |σ| の多項式時間

14. Π ∝ Π′
, Π′
∈ P =⇒ Π ∈ P
C: 言語 φ(Π) を多項式時間で認識するアルゴリズム
1. 言語の認識で、時間 TC (f (σ)) ≤ |f (σ)|kC
2. 全体でも、
T(σ) := TA(σ) + TC (f (σ)) ≤ |σ|kA + (|σ| + |σ|kA )kC
3. T(σ) は、入力長 |σ| の多項式時間

15. NP 完全性
NP 完全な決定問題
任意の Π ∈ NP に対して Π ∝ Π′ となる決定問題 Π′ ∈ NP
Π が NP 完全, Π′ が NP, Π ∝ Π′ =⇒ Π′ が NP 完全
Π ∈ NP 完全を示せば、Π ̸∈ P の強い証拠になる
Π ∈ NP 完全, Π ∈ P なる Π が存在 =⇒ P = NP (予想と矛盾)
Cook の定理
SAT は、NP 完全問題である。
(証明略)

16. NP 困難性
NP 完全 決定問題に対して定義
NP 困難 決定問題ではなくともよいが、その問題が決定性
TM で多項式時間で解かれると、P = NP を意味す
る問題
例:
事例： 有限集合 U, U 上の節集合 C
質問： t(C) = T となる t : U → {T, F} が存在す
るとき、その 1 個を出力せよ

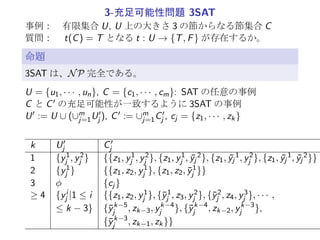
17. 3-充足可能性問題 3SAT
事例： 有限集合 U, U 上の大きさ 3 の節からなる節集合 C
質問： t(C) = T となる t : U → {T, F} が存在するか。
3SAT は、NP 完全である。
SAT ∝ 3SAT
U = {u1, · · · , un}, C = {c1, · · · , cm}: SAT の任意の事例
C と C′ の充足可能性が一致するように 3SAT の事例
U′ := U ∪ (∪m
j=1U′
j ), C′ := ∪m
j=1C′
j , cj = {z1, · · · , zk}
k U′
j C′
j
1 {y1
j , y2
j } {{z1, y1
j , y2
j }, {z1, y1
j , ¯yj
2}, {z1, ¯yj
1, y2
j }, {z1, ¯yj
1, ¯yj
2}}
2 {y1
j } {{z1, z2, y1
j }, {z1, z2, ¯y1
j }}
3 ϕ {cj }
≥ 4 {yi
j |1 ≤ i {{z1, z2, y1
j }, {¯y1
j , z3, y2
j }, {¯y2
j , z4, y3
j }, · · · ,
≤ k − 3} {¯yk−5
j , zk−3, yk−4
j }, {¯yk−4
j , zk−2, yk−3
j },
{¯yk−3
j , zk−1, zk}}

18. t が C を充足していれば、以下のように t′ が C′ を充足:
1. k = 1 では、{y1
j , y2
j } の {T, F} は任意。
2. k = 2 では、{y1
j } の {T, F} は任意。
3. k ≥ 4 では、t(z1) = F, · · · , t(zl−1) = F, t(zl ) = T として、
l = 1, 2: t′(yi
j ) = F (1 ≤ i ≤ k − 3)
3 ≤ l ≤ k − 2: t′(yi
j ) =
{
T (1 ≤ i ≤ l − 2)
F (l − 1 ≤ i ≤ k − 3)
l = k − 1, k: t′(yi
j ) = T (1 ≤ i ≤ k − 3)
逆に、t′ : U′ → {T, F} が C′ を充足させれば、t′ の定義域 U′ を
U に制限して、C を充足させる t : U → {T, F} が得られる。
SAT の事例 U, C が mn の多項式の長さで記述でき、決定的 TM
を用いて，その長さの多項式の時間で 3SAT の事例が計算